Coevolution of craton margins and interiors during continental break-up

Mapping the great escarpments

We model escarpment features using the SRTM void-filled 15-arcsec GMTED2010 datasets digital elevation models (DEMs) from the United States Geological Survey (USGS). In the ESRI ArcMap 10.7.1 geodatabase, DEMs are mosaicked to produce composite raster DEM datasets, which we then use to map escarpments (in the World Geodetic System 1984 (WGS84) geographic coordinate system), using the Spatial Analyst toolset (slope, aspect and curvature). We then generate 100-m contours for the DEMs using the Spatial Analyst contour tool.

Triangulated Irregular Network (TIN) surfaces are generated using the Create TIN (3D Analyst) tool from the 100-m contour polyline datasets. TIN generation uses the Delaunay method of triangulation and WGS84 Transverse Mercator projected coordinate system. TIN surfaces are composed of mass points (TIN nodes), hulls and breaklines (hard and soft). The hard breaklines generated across TIN surfaces isolate breaks in slope that characterize escarpments. Isolation of hard breaklines (export as a separate polyline layer) is carried out using the TIN Line (3D Analyst) tool. We then use manual editing to isolate those breaklines that represent escarpments by alternating between slope, aspect, DEM and curvature base layers.

Characterizing escarpment orientations

We next compare the orientation of discrete segments of escarpments and their associated COB (Extended Data Fig. 2). The mapped distributions of COBs are well established and described in key syntheses of plate-tectonic data^59,60. However, we expect COBs to have some associated uncertainties, largely because these are zones rather than precise linear boundaries. For context, the global mean half-width of the COB ‘transition zone’ is approximately 90 km (ref. ⁶¹). As such, our distance analyses (Fig. 1g) described below is expected to carry uncertainties of ±90 km. In our analysis, we do not explicitly account for uncertainties in estimated distance to a given rift section, because these uncertainties are expected to be spatially correlated (that is, the same uncertainty value would apply to all points along a specific escarpment). COBs are exported from the open-source plate-tectonic software GPlates^59,60 (https://www.gplates.org/). To enable this comparison, it is necessary to generate shapefiles for the escarpments with roughly equivalent complexity (degree of cartographic generalization) as the associated COBs. To achieve this, we use the open-source geographic information system applications QGIS (v3.16; https://www.qgis.org/) and GRASS (https://grass.osgeo.org/). Calculations are performed in the statistical computing package R (ref. ⁶²; https://www.r-project.org/), using libraries sf (Simple Features)⁶³, geosphere⁶⁴, lwgeom and nngeo⁶⁵.

We use a buffer to find the midline, or skeleton (simplified escarpment), in GRASS. This is done by: (1) converting each escarpment from WGS84 (EPSG:4326) to an appropriate projected coordinate system with units of metres, not degrees; (2) generating a (merged) 50/100/500-km buffer around each escarpment; (3) reducing by buffering again by −45/−99/−495 km; (4) applying the v.voronoi.skeleton function to compute the midline. These simplified shapefiles are then read into the R package to estimate the difference in tangent between the escarpment and continent boundary using the following procedure.

We read in these simplified escarpment and COB shapefile and define points (p(i)) every 10 or 50 km along each escarpment line. At each point, p(i), we then find the tangent, Tp(i), using the points either side (±10 or ±50 km) of the point of interest (Extended Data Fig. 2). We approximate the tangent by taking the line between p(i − 1) and p(i + 1). We then calculate the perpendicular to the tangent, L(i), and define the closest point of intersection, x(i), of line L(i) with the COB. Next, we calculate the tangent of the COB at x(i), Tx(i). We approximate Tx(i) by generating a 10-km or 50-km buffer around the point x(i). We then find the points of intersection of Tx(i) and the circular buffer (at which the boundary line enters and leaves the buffer) and use the line between these intersection points to estimate the angle. Finally, we calculate the difference (in degrees) between the tangents Tp(i) and Tx(i) and then the distance between points p(i) and x(i) (Fig. 1g–h, Extended Data Fig. 3).

Analysing distances between escarpments and COBs

The escarpment polylines are exported from ArcGIS as shapefiles, matching the format of the COB files. We analyse the first-order spatial and topological attributes of both features using the R package, specifically, the sf⁶³, lwgeom, nngeo⁶⁵ and geosphere⁶⁴ packages.

Nodes are defined at a spacing of every 10 km along both escarpment and COB polylines. The original coordinate reference system, GCS WGS84, is converted to appropriate EPSG codes for each region, allowing us to calculate distances in metres. Escarpment shapefiles are subsequently cleaned and converted to spatial features objects. Bounding boxes (buffer/crop) are defined for COB files, increasing the efficiency of searching for the closest point between escarpment and COB nodes. After cropping is complete, COB shapefiles are converted to spatial features objects. We use the dist2Line function to calculate the shortest distance in metres between escarpments and COBs (Fig. 1g and Extended Data Fig. 3a–c), with mean distances calculated using the ddply package⁶⁶. Standard deviations are calculated for each plot using the sd function in the stats package in R.

Lithospheric-thickness analysis

We analyse lithospheric-thickness distributions for the escarpments using two different global reference models, LITHO1.0 (ref. ⁴¹) and LithoRef18 (ref. ⁴²). We perform surface interpolation from the vector points map by splines (0.1° cell size) using the GRASS function v.surf.rst. Next, we generate regular points along the length of escarpment shapefiles at 1.0° (approximately 110-km) intervals, using a QGIS vector geometry tool (points along a geometry). This chosen resolution is broadly commensurate with the resolution of the global models^41,42. Using these specified sampling points, we then use the Point Sampling Tool in QGIS to obtain lithospheric-thickness values at each point from the interpolated raster map, and visualize the results for each escarpment using the boxplot function in Matlab R2021b (https://www.mathworks.com/products/matlab.html) (Fig. 1g). The range of lithospheric-thickness estimates for each escarpment using both of the above models are given in Extended Data Fig. 3g. It must be noted that LITHO1.0 returns what we suggest to be high estimates, being on average 10–15% higher than the corresponding LithoRef18 values (Extended Data Fig. 3g). This discrepancy probably arises because the density structure and geometry of boundaries in LITHO1.0 are not optimized to satisfy field data and lithospheric-thickness proxies, which may result in overestimation of the LAB beneath thick continental lithosphere⁴¹. Therefore, although we provide both measures for completeness, we consider the LithoRef18 values to give a more accurate picture of lithospheric thickness beneath the escarpments.

Thermomechanical models

We use the finite element code ASPECT^67,68,69 to compute the dynamic evolution of lithosphere and asthenosphere over a 100-Myr period. This geodynamic software solves the conservation equations of momentum, mass and energy for materials undergoing viscoplastic deformation⁷⁰. We thereby use experimentally derived flow laws that account for temperature, pressure and strain-rate-dependent rheologies (Extended Data Table 1). The models are driven kinematically by prescribing velocity boundary conditions at lateral sides. The simulations generate a narrow rift that migrates laterally⁷¹, leading to a delay of lithospheric break-up. In agreement with previous work, pressure gradients beneath the rift induce pronounced rotational flow patterns⁷² within the asthenosphere. This flow destabilizes the base of the thermal lithosphere adjacent to the plate boundary, forming Rayleigh–Taylor instabilities that evolve self-consistently by sequential destabilization. Next, we describe the geometric and thermomechanical setup, along with the model limitations.

The domain of our reference model (Fig. 2) is 2,000 km wide and 300 km deep and consists of 800 and 120 elements in the horizontal and vertical directions, respectively. We chose a vertical model extent of 300 km depth to encompass the low-viscosity asthenospheric layer that is particularly prone to accommodating rapid mantle flow (an extent of 410 km is also tested). Although the lower boundary of this weak layer is not well defined, a model depth of 300 km includes: (1) the region beneath the lithosphere in which seismic anisotropy indicates a high degree of deformation (for example, ref. ⁷³); (2) the depth range at which dislocation creep dominates deformation, leading to particularly low viscosity (for example, Fig. 10c in ref. ⁷⁴); and (3) the highest depth at which carbonated melts can be expected to further reduce rock viscosity (for example, ref. ⁷⁵). In our model, the initial distribution of material involves four homogeneous layers: 20-km-thick upper crust, 15-km-thick lower crust, 125-km-thick mantle lithosphere and 140-km-thick asthenosphere. To initiate rifting in a predefined area, we define a weak zone that features a 25-km-thick upper crust and 100-km-thick mantle lithosphere representing typical mobile belt conditions⁴¹. These layer thicknesses gradually transition to ambient lithosphere over about 200 km. For visualization purposes, we distinguish a 30-km-thick asthenospheric layer beneath some parts of the lithosphere as a simplified representation of metasomatized mantle.

The flow laws of each layer represent wet quartzite⁷⁶, wet anorthite⁷⁷, dry olivine⁷⁴ and wet olivine⁷⁴ for upper crust, lower crust, mantle lithosphere and asthenosphere, respectively (see Extended Data Table 1 for rheological and thermomechanical parameters). Our model involves frictional strain softening defined through a simplified piecewise linear function: (1) between brittle strain of 0 and 1, the friction coefficient is linearly reduced by a factor of 0.25; (2) for strains larger than 1, the friction coefficient remains constant at its weakened value. Viscous strain softening is included by linearly decreasing the viscosity derived from the ductile flow law by a factor of 0.25 between viscous strains 0 and 1.

In our reference model, we use velocity boundary conditions with a total extension rate of 10 mm y^−1, equivalent to 10 km Myr^−1. To test the sensitivity of our overall findings to this extension rate, we varied the extension velocity to slow (5 mm y^−1) and fast (20 mm y^−1) (Supplementary Videos 2 and 3, respectively). In these cases, we found that the process of sequential delamination still occurs as described in the reference model. Furthermore, we conducted two model runs to assess the influence of time-dependent extension velocities and verified that, in these cases, the key results remain unchanged. Material flux through the left boundary is balanced by a constant inflow through the bottom boundary. The top boundary features a free surface⁶⁹. For simplicity, we fix the right-hand side of the model. However, we verified that our conclusions do not change substantially if extension velocities are distributed symmetrically at both side boundaries (Supplementary Video 1). For example, in this symmetric model, three instabilities are generated with migration rates of 20 and 16 km Myr^−1 (when measured relative to the absolute reference frame) that translate to 15 and 11 km Myr^−1, respectively, when accounting for rightward advection with 5 km Myr^−1 (that is, in the reference frame of the continent). These values fit reasonably well to the reference model (15–20 km Myr^−1; Fig. 2).

The surface and bottom temperatures are kept constant at 0 °C and 1,420 °C, respectively, whereas lateral boundaries are thermally isolated. The initial temperature distribution is analytically equilibrated along 1D columns before the start of the model by accounting for crustal radiogenic heat contribution, thermal diffusivity, heat capacity and thermal boundary conditions. We associate the bottom of the conductive lithosphere with the initial depth of the compositional LAB at a temperature of 1,350 °C. Below the lithosphere, the initial temperature increases adiabatically with depth. To smooth the initial thermal gradient between the lithosphere and the asthenosphere, we equilibrate the temperature distribution of the model for 30 Myr before the onset of extension.

The development of sequential instabilities and their migration velocity is a function of sublithospheric viscosity¹¹. The occurrence of seismic anisotropy in the shallow asthenosphere suggests that deformation is dominated by dislocation creep⁷⁸. We therefore use a nonlinear flow law using experimentally derived values for dislocation creep in olivine⁷⁴, such as an activation energy of 480 kJ mol^−1. Previous numerical models have shown that the occurrence of delamination is particularly controlled by the activation energy⁷⁹, with a permissible range of 360–540 kJ mol^−1. To explore the effect of activation energy on migrating instabilities, we conducted modelling experiments in which we varied the asthenospheric activation energy while keeping all other parameters constant. By decreasing the activation energy to 440 kJ mol^−1, the viscosity of the shallow asthenosphere and metasomatized layer became roughly two times smaller. As a result, the lateral migration rates of the instabilities generated by this model were about twice as fast as in the reference model. The proportionality further agrees with estimates of migration speed from analytical considerations¹¹. Rheological experiments as well as numerical and analytical modelling therefore indicate that the process of sequential delamination is plausible and that migration takes place at rates of tens of kilometres per million years—a speed that is comparable with the inferred wave of surface erosion within the plateau (Fig. 3).

Finally, we assessed the potential impact of the chosen model domain on our findings by increasing the depth to 410 km (Extended Data Fig. 5 and Supplementary Video 4). We chose this depth extent to avoid complexities associated with phase changes in the mantle transition zone. Most notably, this model shows that the process of sequential delamination occurs independently of the depth of the model domain. The migration velocity of the instabilities in this run is slightly more variable than in the shallower reference scenario but averages at a value of 15–20 km Myr^−1, identical to that of the reference model. Notably, the spacing between two instabilities does not increase proportionally to the height of the convection cell. The 410-km model features convection cells approximately twice as high as in the reference model, whereas the distance between instabilities, when measured at the depth of the TBL, remains very similar (that is, the mean spacings for the reference model and 410-km model are 269 and 255 km, respectively). These observations lead us to conclude that, for the models to yield meaningful results, the TBL must be thin relative to the height of the convection cell—a criterion met in all cases described in our paper.

When interpreting our results, the following model limitations must be kept in mind. (1) We focus on first-order thermomechanical processes and do not explicitly account for chemical alterations, melt generation and magma ascent. (2) For simplicity, we assume that the initial depth of the LAB does not vary on the thousand-kilometre scale. We verified that gradual changes in morphology of the initial LAB did not affect our overall conclusions. (3) For simplicity, we neglect further processes in our generic modelling strategy that may be deriving from the impingement of mantle plumes, along-strike lithospheric heterogeneities and large-scale mantle-flow patterns.

Analytical models and Monte Carlo simulations

We performed analytical modelling to estimate the magnitude of uplift and denudation resulting from the removal of the cratonic lithospheric keel, as described in ref. ¹¹, using the parameters provided in Extended Data Table 2. It must be noted that this experiment considers only the density contrast between colder lithosphere and hotter asthenosphere¹¹ and does not include compositional changes, for example, related to melt metasomatism. We assess the likely magnitude of erosion and denudation (equations (1)–(3)) by performing a Monte Carlo simulation, sampling parameters from probability distributions. We applied both uniform and beta distributions to represent natural variability in the parameters (Extended Data Table 2). For simplicity, we assume beta distributions with a standard deviation of 30% of the mean.

For the unstable TBL or keel, we considered a thickness (b) range of 17–18 km, as inferred from xenolith geotherm analysis¹¹ (see Extended Data Fig. 6 for a schematic). This value represents half of the total thickness of the TBL, with the LAB situated near its middle. Similarly, the temperature increase across this layer, ΔT, is expected to lie in the range 140–165 °C, based on xenolith geotherm analysis¹¹. Because our primary focus is on the southern Africa region, in which the most thermochronological constraints are available (Fig. 3), we used a range of densities of the eroded rock (ρ_c) of 2,800–3,000 kg m^−3 (ref. ⁸⁰) to reflect a dominantly basaltic catchment in this region during the Cretaceous^5,25,48. The uniform and beta distributions yield mean and maximum values for denudation of approximately 0.8 and 1.6 km, respectively (Extended Data Fig. 7). Over an extended time frame, that is, 10⁶–10⁷ years, dynamic mantle support will invariably increase this value.

Thermochronological analysis

In our study, we test a geodynamic model (Fig. 2) by determining the spatial trends of, and total amount of, cooling (related to exhumation) over a specific interval, that is, 180–0 Ma. Because we are concerned with the exhumation history of cratons, we mainly restrict our study to those regions inboard of escarpments (that is, hinterland plateaus). We compile the thermal histories for a total of 47 sites across arguably the most classic example, the Central Plateau of Southern Africa (Extended Data Fig. 4). Details on the thermal models used in the original thermochronology work are provided in Extended Data Table 3. To estimate the most probable timing of cooling and evaluate uncertainties across the 47 plateau sites (Extended Data Table 3), we use published best-fit t–T paths, upper and lower envelopes encompassing time uncertainty, and individual model thermochronology curves (Extended Data Table 3). This information allows us to estimate the maximum temperature drop (max(dT/dt)) and its corresponding timing (\({t}_{\max }\frac{{\rm{d}}T}{{\rm{d}}t}\)), together with associated model uncertainties. Estimation of \({t}_{\max }\frac{{\rm{d}}T}{{\rm{d}}t}\) is not exact, particularly for sites that exhibit prolonged, gradual temperature change or with highly uncertain thermal histories. Different sources also estimate and present thermochronological uncertainty in different ways. Thus, for each site, we calculate a best estimate for \({t}_{\max }\frac{{\rm{d}}T}{{\rm{d}}t}\) (denoted t_mid in Extended Data Table 3), together with a range (that is, t_min and t_max) accounting for available (published) model data and uncertainty estimates. These are shown as error bars in Extended Data Fig. 8 and are summarized in Extended Data Table 3. Using t_min, t_mid and t_max, we then fit a simple beta distribution to enable Monte Carlo sampling of the time uncertainty at each site (Fig. 3a,b). We apply the same approach to 24 sites from Eastern Brazil (Extended Data Figs. 10a). Here several sites (n = 4) show a distinct two-stage cooling history, which we accommodate in our analysis (Extended Data Fig. 10d).

For each thermochronology site, we interpolate to a regular (0.1-Myr resolution) time series over the period 180–0 Ma. We assume no (notable) temperature changes beyond the limits of the thermochronology data provided. We calculate the average temperature drop (dT/dt, in °C Myr^−1) using a moving, symmetric window of ±0.9 Myr at each 0.1-Myr time step. The total temperature drop is calculated from the best-fit curves (dT total (bf) in Extended Data Table 3) and used to estimate the exhumation rate. Note there is no available temperature drop estimate for site Br90-39⁸¹ .

For all sites, t_mid is the best estimate of the timing of maximum temperature drop obtained from the best-fit curve for that locality. For sites at which we have upper, lower and best-fit curves, t_min and t_max are defined as the minimum and maximum time at which dT/dt ≥ 60% of max(dT/dt) over all three curves. Note that for some sites (for example, refs. ^29,50,53), the upper and lower curves are described as defining the upper and lower 95% credible interval. For other sites (for example, ref. ⁸²), the upper and lower curves define the ‘good-fit’ envelope.

Where we have a best-fit curve and further minimum/maximum time estimates, we define t_min as the earlier time of either the minimum estimate or the first point at which dT/dt ≥ 60% of max(dT/dt) on the best-fit curve. Similarly, t_max is defined as the later time of either the maximum estimate or the latest point at which dT/dt ≥ 60% of max(dT/dt).

For sites with several thermal history model runs, we calculate the earliest and latest times at which dT/dt ≥ 60% of the maximum over all model realizations, including ‘best’, ‘good’ and ‘acceptable’ model runs. For a given site, we define t_min as the 10th percentile minimum time and t_max as the 90th percentile maximum time estimate calculated from all model runs. The best estimate t_mid is defined as the time of the peak max(dT/dt) for the best-fit model run. For sites at which we do not have individual model runs, the best estimate t_mid is defined as the midpoint of the time interval at which dT/dt ≥ 90% of max(dT/dt) for the best-fit curve, to accommodate the lower resolution of these data. This approach gives uncertainty estimates that should be broadly comparable across localities.

We used the same published thermochronological constraints for 46 sites to estimate the total amount of exhumation at each site (Fig. 3b and Extended Data Table 3). Using best-fit curves for each site, we compute the maximum modelled temperature drop T_max − T_min over the interval 180–0 Ma. We then divide the temperature difference (T_max − T_min) by the geothermal gradient, sampling from a beta distribution to capture the known uncertainty in the geothermal gradient. Geothermal gradients in Southern Africa today are estimated to range between 15 and 33 °C km^−1 on average (ref. ⁸³). Naturally, no single value of geothermal gradient can apply to the entire plateau. Hence, we consider a compilation spanning the present-day Southern African region⁸⁴ to capture the plausible range. We represent uncertainty in the geothermal gradient by a beta distribution on the interval [10, 60] °C km^−1 (informed by ref. ⁸⁴) with a mean of 28 °C km^−1, standard deviation 7.5 °C km^−1 and parameters α = 3.3264 and β = 5.9136. The upper end of this range accounts for the very high values (38–46 °C km^−1) favoured by Stanley et al.¹⁸ for Cretaceous Southern Africa. Distance is the shortest distance measured from the point location of the thermochronology site (longitude/latitude; Extended Data Table 3) to the COB line, calculated in R using the dist2Line function from the geosphere package⁶⁴. Uncertainty in distance is again assumed to be ±90 km (see the section ‘Characterizing escarpment orientations’). We sample a distance offset using a beta distribution on the interval [−90, 90] km, with a mean of 0 km and standard deviation of 36 km, with parameters α = β = 2.625. In total, 20,000 samples are generated for both the geothermal gradient and distance offset for each thermochronology location (Fig. 3b).

Finally, we plot profiles of AFT and AHe ages across the Southern African (Extended Data Fig. 9) and Eastern Brazilian plateaus (Extended Data Fig. 10), using the data compilations of Stanley et al.¹⁸ and Novo et al.⁸⁵, respectively. Here we constructed the profiles across the plateaus perpendicular to the continental margins and escarpments. In the case of Southern Africa, we avoided the southern part of the plateau in which the escarpment strikes roughly east–west, as it would cause interference (sampling parallel to an escarpment at which young ages are expected). In Eastern Brazil, we aligned our profile to capture the region at which most AHe ages exist and extend further inland. We include a buffer of 100 km to capture as many points as possible along a given section. In the case of Southern Africa, we plot the closest distance between the measurement point (AFT or AHe) and the escarpment at the western end of the profile (Extended Data Fig. 9). The distances were measured using the dist2Line function in the R package geosphere⁶⁴, following the procedure outlined above for the escarpment analysis.

Accounting for potential kimberlite-related cooling

The cooling detected by thermochronology studies can most parsimoniously be explained by denudation (for example, refs. ^5,24,25,48). However, a component of the inferred cooling across Southern Africa (Fig. 3 and Extended Data Fig. 8) is feasibly related to magmatic cooling, for example (in the case of cratons), associated with kimberlite volcanism. We identify these potential cases to evaluate where the cooling is more likely to be denudational. Given the typical durations of cooling modelled in previous thermochronology investigations, these trends are unlikely to be driven by kimberlite magmatic cooling. Kimberlites are monogenetic volcanoes with probable eruption durations of hours or months⁸⁶. Further, it has been shown that the largest kimberlite diatremes should cool down to ambient temperatures within 2–3 kyr of eruption onset⁸⁷. Nevertheless, to explore whether such cooling could be important, we investigate all cases in which a kimberlite eruption age overlaps in time and space with the known locations of cooling (that is, thermochronology sites). In cases in which there was overlap, we completely (and conservatively) remove modelled cooling for a fixed time interval either side of the kimberlite radiometric age, using the kimberlite age compilation of Tappe et al.⁸⁸. Specifically, we remove all cooling for sites at which there is a record of a kimberlite eruption dated within ±2 Myr (relative to the thermochronology time) and conservatively within a radius of 50 km, using thermochronology coordinates provided in Extended Data Table 3. Those purely denudational trends and those that account for potential kimberlite cooling are distinguished as red and black lines, respectively (Extended Data Fig. 8a). The above approach is considered conservative given the small length scales of kimberlite pipes (typically hundreds of metres) and that kimberlite eruptions (lasting on the order of several thousand years) and cooling of diatremes are known to be short-lived phenomena encompassing several thousand years at most (refs. ^86,87).

Distances were estimated from longitude/latitude coordinates for the thermochronology sites and kimberlite records using the R geosphere⁶⁴ distm function, using distGeo to obtain an accurate estimate of the geodesic, based on the WGS84 ellipsoid. Our analysis shows that even using conservative spatial and temporal bounds, cooling directly linked to kimberlite volcanism makes, if anything, a comparatively minor contribution to the overall cooling trends (Extended Data Fig. 8a). Notably, the period experiencing the most frequent (possible) kimberlite-related cooling between 100 and 80 Ma is associated with a marked increase in sediment accumulation rates offshore Southern Africa; previously, this event has been linked to a concomitant massive increase in onshore denudation⁸⁹. Hence we argue that the observed cooling is largely denudational rather than magmatic (corroborating earlier suggestions^48,89). We instead argue that the temporal coincidence between some kimberlites and modelled cooling is probably related to a common fundamental underlying mechanism (for example, lithospheric delamination), as opposed to a causal link between kimberlites and cooling.

Landscape-evolution model

To investigate the evolution of topography, total erosion and erosion rate over time, we use the Fastscape landscape-evolution model, described in detail in ref. ⁵⁸ (see ‘Code availability’). The model solves the SPL, which states that the rate of change of surface elevation, h, owing to river incision is proportional to local slope, S, and discharge, ϕ, put to some powers, n and m, respectively:

This relationship can be traced back to the pioneering works of Gilbert⁹⁰ and, from a computational point of view, Howard et al.⁹¹. Assuming that rainfall is relatively uniform (compared with slope and drainage area), the relationship is often simplified to yield:

the canonic form of the SPL, in which A is drainage area⁹². It is also known as the stream power incision model (SPIM) and its appropriateness at representing the main driver of landscape evolution in high-relief areas has been amply discussed⁹³. In particular, much work has focused on the value of the exponents (m and n). It is unclear what the optimum values should be or on what they depend, but the ratio of the two, m/n, is close to 0.5 and can be derived from the concavity of river profiles. Here we used n = 1 and m = 0.4, as is commonly done. The method used to solve it is fully described in ref. ⁵⁸. The other important equation that is solved is the biharmonic equation representing the elastic isostatic flexure of the lithosphere:

in which D is the flexural rigidity, given by:

in which E is Young’s modulus, T_e the effective elastic plate thickness, ν Poisson’s ratio, w the deflection of the lithosphere caused by the difference in height, h, and a reference value h₀, g the gravitational acceleration and ρ_s and ρ_a are the surface and asthenospheric densities, respectively. It is solved using the spectral method developed in ref. ⁹⁴. The version of Fastscape used in our study has been used in many publications, including ref. ⁹⁵.

For our purposes, the model captures the surface evolution of a continent over 50 Myr. The initial plateau topography (h₀) was set to 500 m (considered broadly representative for Mesozoic South Africa⁹⁶ and stable cratons globally¹⁵) and an erodibility coefficient, K_f, was set to 1 × 10^−5 m^1−2m per year, in which m is the area exponent in the SPL (m = 0.4). The topography and erosion characteristics were modelled using a Gaussian-shaped wave of uplift with a velocity of 20 km Myr^−1 and half-Gaussian width of 200 km, with both properties informed by our thermomechanical simulations (Fig. 2). The amplitude was set to achieve 2,000 m of uplift after isostatic adjustment and taking into account the initial, pre-existing topography. This uplift wave mimics the dynamic topography generated by convective mantle flow. The maximum uplift rate varies from run to run, as it depends on all the other parameters, including wave width, velocity, relative densities and initial topography. For the ‘fixed’ parameters, that is, wave width, velocity and density ratio, the uplift rate varies linearly with the initial topography, with a range of approximately 1–0 mm year^−1, as the assumed initial topography varies from 0 to 2,000 m.

The topographic response in the model includes a flexural isostatic response with a crustal density of 2,800 kg m^−3 and asthenospheric density of 3,200 kg m^−3, as well as an effective elastic thickness (T_e) of 20 km. This thickness is considered an average value for continental lithosphere/crust⁹⁷ (note that ref. ⁹⁷ argues that values of T_e are often overestimated), which is further supported by the fact that it is not physically possible to ‘pin’ an escapement as a drainage divide if T_e is too high²¹. Any surface erosion in the model leads to further isostatic uplift, meaning that any change in topography related to erosion requires about 6–7 times the amount of erosion. This value is broadly in line with our independently derived analytical model (equations (1)–(3)) which predicts up to 10 times amplification of uplift by erosion.

In terms of boundary conditions, the left-hand and right-hand sides of the model have a fixed boundary at h = 0, representing the ‘base level’, which—in this case—corresponds to the ocean. The other boundary conditions are defined as periodic, meaning that a river flowing towards one of these boundaries (north or south) reappears on the other side of the model (south or north). This approach is commonly used when solving the SPL to avoid boundary effects. The routing algorithm⁹⁸, which computes the direction of water flow, assumes that every drop of water falling on the model must eventually escape through one of the base-level boundaries. However, the specific path of escape is not predetermined; rather, it is internally computed from the local slopes and thus following the topographic evolution set by the uplift and fluvial erosion/carving. In the model results (Fig. 4), some water escapes through the left boundary and some escapes through the right boundary. Whether the escarpment becomes a divide and later evolves into a ‘pinned divide’ is not prescribed but instead results from a delicate balance between uplift and erosion. These points have been extensively discussed in the literature and are summarized in ref. ²¹.

We conducted a sensitivity analysis by assessing the range of values for h₀ that would provide a good fit to observations. To do this, and to determine the quality of our model, we calculated a misfit function assuming that the optimum plateau height is 1,650 ± 250 m (in line with expectations^32,33 and the present-day topography, which is 1.0–1.5 km on average¹⁵; Fig. 1d), optimum denudation is 2,750 ± 500 m (refs. ^{5,25,29,31,48,50,53}) and the optimum final position of the divide is 650 ± 100 km (assuming that the wave started moving at 500 km from the left-hand side of the model). As we are concerned with the final position of the drainage divide, we use the upper end of our empirical estimates of escarpment position (Fig. 1g). We perform 120 numerical experiments of landscape evolution to calculate the misfit function (Fig. 4d and Extended Data Figs. 11 and 12). A misfit value less than 1 indicates that realistic conditions are met (that is, the model predicts values that fall between the optimum value ± the assumed uncertainty) (white contours in Fig. 4d). Our analysis also identifies the maximum limit of acceptable values for K_f that would allow the plateau to survive until today (Fig. 1d), without prohibitively high levels of erosion (dashed line in Fig. 4d). We find that the range of values for h₀ that provide a good fit to existing constraints is from approximately 0 to 1,000 m. On this basis, our preferred model (Fig. 4a–c) has a misfit value less than 1 and obeys observational constraints.

Predicting thermochronology ages in the surface-process model

To identify model limitations and guide future testing of our geodynamic model (for example, with improved spatial resolution of thermochronology studies and/or extra borehole data), we used Fastscape to predict AFT and AHe ages across the plateau and through time (Fig. 5) using the same model configuration as before (Fig. 4). To do this, we solved the 1D conduction/advection equation at each point to predict thermal histories, from which ages are then computed. For this, we use the erosion-rate history predicted by Fastscape. Our predictions exclude radiogenic heating effects, leading to an initially linear conductive steady-state geothermal gradient—a standard practice when predicting ages for relatively low-temperature systems such as AHe and AFT that are not very sensitive to the curvature of the geotherm. The ages are predicted from the thermal histories, using the same algorithms as in the Pecube software^99,100, based on solving the solid-state diffusion equation in 1D inside a grain of given size assuming a cylindrical geometry for AHe using the algorithm in ref. ¹⁰¹ and on an annealing algorithm using the parameters in ref. ¹⁰² for AFT. Here the effects of radiation damage are omitted, potentially changing the absolute age values of the predicted ages, but—notably—not the first-order patterns of interest here. Our models cover a 50-Myr period, with an extra 50 Ma added to computed ages to account for an assumed ‘quiet’ post-uplift phase since the late Cretaceous, consistent with present-day low erosion rates (as measured by cosmogenic methods, for example, ref. ¹⁰³), even along the escarpment. Note that, east of the last position of the mantle convective instability in our model (Fig. 4), the ages return to their assumed ‘un-reset’ value, that is, ≥100 Ma (Fig. 5).

Testing broader applicability

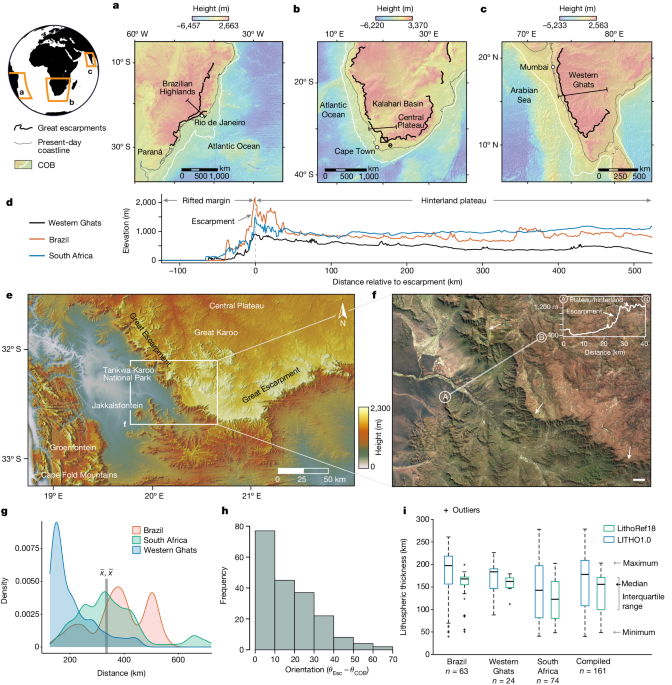
To explore the broader applicability of our model, we consider the Namibian margin as well as the escarpments and associated plateaus in Eastern Brazil and the Western Ghats (Fig. 1 and Extended Data Fig. 1). First, rifting commenced along the Namibian margin between 145 and 139 Ma, followed by continental break-up occurring from about 116 to 113 Ma (refs. ^54,104). Indeed, inverse modelling of AHe dates from the Namibian margin, combined with AFT data, reveals an early abrupt cooling phase (10 °C Myr^−1) from 130 to 100 Ma (ref. ¹⁰⁵)—probably related to rift shoulder uplift and escarpment retreat—which mirrors South African and Brazilian patterns during continental break-up (see main text). Importantly, offshore AFT analysis and sediment accumulation records overlapping this cooling phase (from 110–80 Ma) indicate the subsequent removal of Precambrian material from the cratonic interior¹⁰⁶, supporting a spatiotemporal shift inland in the locus of uplift and denudation. Consistent with this, large-scale denudation (that is, 2–3 km in total from 140 to 70 Ma) extended several hundred kilometres inboard of the escarpment¹⁰⁷, sampling Precambrian lithologies from the Damara Belt and Otavi Group. More than half of this denudation occurred after rifting, closely matching observations in South Africa (Fig. 3) and consistent with our landscape-evolution models (Fig. 4b). Thermal history models across this broader region indicate near-continuous exhumation since the Upper Cretaceous¹⁰⁸, suggestive of a continuing process. This is again consistent with the concept of sequential migration, with uplift and denudation occurring successively further inland. We can test this concept by considering the distance from the site of exhumation to the nearest COB. Our model (Figs. 2 and 4) predicts substantial exhumation in the interior plateau regions of Southern Namibia around 65–70 Ma. Supporting this, Gallagher and Brown¹⁰⁷ infer 1–2-km denudation in this region during this period, whereas Wildman et al.¹⁰⁶ report a Damara uplift phase within a similar time frame from 65 to 60 Ma. Although the specifics of the migration of uplift and denudation into the continental interior remains uncertain given available data, collectively, these observations support a common mechanism across the wider Southern African region associated with rifting and break-up.

Like the Namibian margins, Eastern Brazil underwent rifting at about 139 Ma and continental break-up at around 118 Ma (ref. ⁵⁴). To examine the applicability of our model to Eastern Brazil, and noting a paucity of thermal history analyses in the continental interior, we initially focus on the analysis in ref. ⁵⁷, which extends nearly 1,000 km inland, enabling a comparison with trends on the Southern African plateau. We also consider AFT and AHe ages from across Eastern Brazil using a recent compilation of 1,248 ages⁸⁵, predominantly featuring young ages in lowlands and near escarpments. As predicted by our landscape-evolution models (Figs. 4b and 5), we observe younger ages near the escarpments owing to high magnitudes of total erosion there (Extended Data Fig. 10a). We constructed a profile of AHe and AFT ages in the section in which AHe ages extend furthest inland and observed that, although scattered, the AHe ages decrease nearer the escarpments and decrease with distance into the interior of the plateau (Extended Data Fig. 10c), similar to the observed trend in Southern Africa (Extended Data Fig. 9b).

Our landscape models predict that AFT ages may be much older on the plateau (Fig. 5). This is observed in the São Francisco Craton and marginal orogens, in which old ages (predominantly 350–280 Ma) relate to the Gondwanide orogeny (Extended Data Fig. 10a,b). It is perhaps not surprising that the AFT ages are barely, if at all, reset in the continental interior, in contrast to AHe (Extended Data Fig. 10a,c). This is because the closure temperature for the AFT system is higher than that for AHe (Fig. 5) and considering that the total exhumation across the highlands is low, at about 1.0–1.5 km (Extended Data Fig. 10e). Further, in a study of Northeastern Brazil, Sacek et al.¹⁰⁹ recognized that the high variability in erodibility, and consequently AFT ages, may result from the formation of duricrust layers or cangas, which could lead to highly variable erosion rates, even under a smoothly varying uplift rate. This factor is probably important in the studied region as well.

Nonetheless, many interior regions have experienced some degree of Cenozoic unroofing. Harman et al.⁵⁶ identified early cooling around 130 Ma at the São Francisco Craton margins during rifting, followed by a later event (circa 60–80 Ma) affecting the cratonic interior of Northeastern Brazil, analogous to the uplift and denudation history of Namibia. Although Harman et al.⁵⁶ attribute this to intracratonic basin inversion (considering the time separation, these authors rule out a role for rifting), the observed uplift of interior regions at these times is consistent with our model predictions (Extended Data Fig. 10c–e), thus offering a new explanation. Extrapolating from Southern African trends (that is, migration rates of the erosional wave; Fig. 3d), our model would predict exhumation onset in these more distal interior regions around 80–25 Ma, as well as recent and continuing exhumation. The observed cooling from about 80 Ma to the present day supports this prediction^{26,30,56,57,85,110,111}. Although we do not suggest that all cooling in this region—characterized by several geotectonic provinces, cratonic fragments and tectonic weaknesses (for example, ref. ³⁰)—is exclusively linked to mantle instabilities tied to rifting, our model is well supported by existing thermochronological data. The predictions from our model and thermochronology should prompt and inform further measurements, especially AHe analyses, in relatively understudied inland/highland regions of Eastern Brazil.

Testing our model in the Western Ghats is more challenging; however, available data cannot definitively rule it out. The escarpment is associated with the rifting between Madagascar and India, which started around 100 Ma, followed by continental break-up between 86 and 82 Ma (refs. ^54,104) (Extended Data Fig. 1). Another major escarpment along the eastern passive margin of India¹¹² is associated with the earlier separation of India and Antarctica around 125–120 Ma (ref. ⁵⁴). Further rifting and break-up between India and the Seychelles Microcontinent occurred at roughly 66 Ma. Because peninsular India is narrow compared with internally drained continental hinterlands such as Southern Africa and Brazil¹¹³, in the context of our model (Figs. 2 and 4), interior hinterland regions are expected to exhibit interference patterns in exhumation related to the activity of diachronous rift systems. This issue greatly complicates the identification of drivers of post-rift uplift in the continental hinterlands. During the Cretaceous and Cenozoic, regions inboard of the Western Ghats escarpment experienced high denudation rates (ranging from 50 to 150 m Myr^−1, depending on the AFT parameters used) associated with syn-rift and post-rift phases¹¹³, consistent with model expectations (Fig. 4c). Although AFT-derived and mass-balance-derived denudation rates¹¹³ favour a peak in denudation intensity coinciding with Seychelles rifting^114,115, it is hard to exclude the possibility of this signal constituting a lagged response to the Madagascar break-up, with post-rift exhumation targeting interior regions. Future studies can apply thermochronology to test these models.

Further references are cited in the extended data^81,116,117.