All materials and methods were reviewed and approved by the Institutional Review Boards at the Massachusetts Institute of Technology (MIT) (IRB1504007082, IRB1612798217 and IRB2208000727) and the Institute for Financial Management and Research (IRB00007107). We obtained informed consent from all study participants. The studies involved randomization, and we used power calculations to determine our target sample sizes. We include a more detailed summary of our methods in the Supplementary Methods.
Statistical analysis and code
In all analyses, we calculated group means and compared them using two-tailed t-tests. In Extended Data Table 6 and Supplementary Tables 21 and 22, we compared groups using linear regressions. We present these results with and without controls. To calculate standardized indices (for example, when measuring stress), we first standardized the individual outcomes that make up a given index, averaged them and then standardized the final variable to have a mean of 0 and a standard deviation of 1. We conducted all of our analyses in Stata and plotted figures in R.
Study 1
Sample
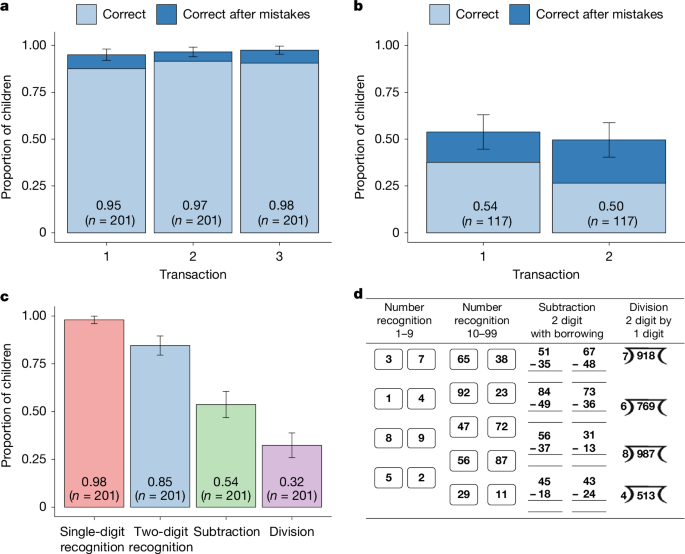
There is no list of all informal (wholesale and retail) markets that employ children in India because child labour is illegal. Therefore we drew a convenience sample of markets in all studies. In study 1, we identified potential markets and then visited them to verify that they employed children. This process identified 92 markets. We drew a convenience sample of working children at each market. An enumerator walked around each market and noted where children were located. We only approached children who appeared to be 16 years of age or younger, were selling goods and sold more than one good. We did, however, stop the survey if we discovered that the child was 18 years of age or older. This led us to include some children who were 17 years of age. In study 1, 201 out of 285 working children whom we approached agreed to participate. Given that the vast majority of children consented to participate, selection on who consents is unlikely to be driving our results, although we cannot rule this out entirely. Of these children, 141 were enrolled in school (average grade attained at the time of testing, 6.24) and 60 were not (average grade attained, 3.67) (Supplementary Table 3).
Survey structure
For study 1, our survey consisted of the following sections: (1) market transactions; (2) consent; (3) ASER written assessment; (4) oral abstract and anchored assessment; (5) hypothetical transactions; and (6) demographics.
Market transactions
In the market transactions section, each working child was approached by two enumerators dressed as regular buyers who purchased two goods (for example, 300 g of beans and 200 g of peas). When goods were sold by the unit (for example, bananas), enumerators bought them by the unit. When they were sold by the kilogram (for example, tomatoes), enumerators bought them by the kilogram or gram. In both cases, enumerators avoided purchasing common quantities (for example, 1 kg or 500 g or 1–2 units) to minimize the probability that children had memorized the prices of the quantities requested.
When a child told the enumerators the amount due, they were asked how they had arrived at that total (for example, by an enumerator who said, ‘I expected it to be less’), which prompted the child to explain their calculation. If the calculation was correct, the enumerators paid and left. If it was incorrect, the enumerators asked the child to verify their calculation (for example, saying ‘Are you sure? How did you get that? Do it again and see’). Regardless of whether the child’s calculation of the amount due was correct, the enumerators offered more money than was due, took the change and left. The use of calculators, paper aids and help from adults was permitted but the enumerator kept a record of each.
In studies 1 and 2a, two other pairs of undercover enumerators repeated the same process, resulting in three transactions per child. One of the three pairs of enumerators revealed their identity and invited the child to participate in the study.
ASER
The ASER is a survey of learning outcomes for school-aged children conducted annually by Pratham, a non-governmental organization in India. ASER is representative of rural India, although in some years, it was also conducted in select urban areas.
Study 2a
Sample
We followed a similar process for identifying children and markets as in study 1. In this study, we conducted the main survey after the first market transaction. We later returned with undercover enumerators to complete the second and third transactions. Of the 442 working children approached, 400 agreed to participate and 344 completed all three transactions (Extended Data Table 2)
Survey structure
The survey consisted of the following sections: (1) market transactions (as in study 1); (2) consent; (3) ASER written assessment (as in study 1); (4) oral abstract and anchored assessment (as in study 1); (5) hypothetical transactions; (6) roundable problems for a subsample of 85 children; and (6) demographics.
Rounding prices in the market
It is common practice for shopkeepers in markets in India to round prices up or down by one or to the nearest multiple of five. In studies 2 and 3, for all market transactions (for working children), pretend market transactions (for school children) and hypothetical transactions (for working and non-working children), we considered the price quoted for an individual good to be correct if it was rounded up or down by one from the exact answer, rounded up or down by five from the exact answer or the exact answer itself. For example, if the exact answer was 35.5 rupees, we would treat 30, 35, 35.5, 36 and 40 as correct answers. We did this because such rounding is common practice and does not reflect the inability of the child to solve problems.
For the combined price of goods 1 and goods 2, we considered any answer that adds the correct (rounded or unrounded) prices of individual goods to be correct. For example, if carrots cost 18 rupees and potatoes cost 32 rupees, we would consider a total price of 52 rupees to be a correct answer; 18 rupees can be correctly rounded to 20 rupees, and 20 rupees plus 32 rupees gives a total of 52 rupees.
For the change provided, we calculated the correct answer by subtracting the true cost of each good from the cash provided (not by subtracting the amount quoted by the child from the cash provided). For example, if we purchased 600 g of apples at 30 rupees per kg and 200 g of potatoes at 20 rupees per kg and gave the child 200 rupees, then we would calculate the exact answer as 200 – (0.6)(30) – (0.2)(20) = 200 – 18 – 4 = 178, irrespective of what the child quoted for the total amount due. We also allowed the same rounding as described for the combined price of goods 1 and goods 2. For example, we would also treat 200 – 20 – 5 = 175 to be correct.
Hypothetical transactions
In study 2a, there were five hypothetical transactions that varied one aspect of the transaction at a time. For example, for a child who sold carrots by the kilogram that day, the first would be a hypothetical problem focused on selling carrots at the familiar price by kilogram. The second problem would be selling carrots at a new price by kilogram, the third, selling carrots at the same new price by kilogram and a second unfamiliar good sold at a new price by kilogram. The fourth problem would be selling a new good, for example bananas, at a new price by units, and finally, selling bananas at the same new price by units and a second unfamiliar good at a new price by units (see Supplementary Methods, study 2a, for more details and examples of the problems). We provided children with pen and paper.
Incentive randomization
Each child was randomly assigned to two versions of the exercises: a version that offered them 10 rupees for every exercise that they answered correctly (in addition to the 200 rupees for participating) and a version that did not offer any incentives.
Roundable problems
In study 2, a subset of 85 working children were given four exercises explicitly designed to encourage the use of decomposition and repeated grouping. To give children maximum latitude to reveal their sensitivity to the base-ten structure, paper and pencil aids were made available to them. In all other respects, the problems mirrored those of the abstract and anchored arithmetic problems from the preceding test. They were not provided any hint that this was a possible strategy to follow. We present the results in Supplementary Table 23.
Solution methods
We collected all the sheets of paper that working children used during the written exercises, hypothetical transactions and roundable problems. We developed a coding system to characterize the calculation strategies used by these children (for example, the number of numbers that children wrote on the page, whether they used tallies or serial numbers, among others) and asked data-entry operators to use these codes to enter data on every sheet of paper. Every sheet was coded twice by two different data-entry operators to identify and correct any inconsistencies in data entry.
Study 2b
Sample
In study 2b, in July–August of 2017, we surveyed 200 children attending 20 government schools located in a 2-km radius of the markets we identified. We selected ten children at random from grade 8 and ten children from grade 9. All school children agreed to participate.
Survey structure
Study 2b consisted of the following sections: (1) consent; (2) pretend market transactions; (3) ASER written assessment (as in study 2a); (4) oral abstract and anchored assessment (as in study 2a); (5) hypothetical transactions (as in study 2a) and roundable problems (as in study 2a); and (6) demographics. We recorded solution methods as in study 2a.
Pretend market transactions
We set up a pretend market in classrooms with plastic goods and money. We told children to imagine they were selling items in a shop and that the surveyor was a customer. We randomized children to sell by kilograms or units. We asked the child to go to the desk at the front of the classroom and select any two items that they wanted to sell. We then checked the goods that they selected had different prices and explained to the child that the prices written were sold per kilogram or by unit. Children were then given plastic money of 300 rupees in small change and told that they could use pen and paper during the transaction if needed. We then followed the same process we used with working children, performing three separate transactions.
Study 3a, wave 1
Sample
We followed a similar sampling strategy to study 2a. Of the 489 working children who completed a market transaction with one of our surveyors, 372 agreed to participate and completed the full survey. We present the characteristics of our study 3 sample in Supplementary Table 24.
Survey structure
Study 3a, wave 1 consisted of the following sections: (1) market transactions (as in studies 1 and 2a); (2) consent; (3) hypothetical transactions and calculation explanations; (4) oral abstract subtraction and hints (with the order of (3) and (4) randomized); (5) market maths word problem; (6) market maths word problem with hints; (7) oral abstract division; and (8) demographics and stress measures.
Hypothetical transactions and calculation explanations
We asked children two hypothetical transaction questions. They were allowed to attempt the question twice if they were initially incorrect. After each question, we asked children how they solved the problem. We audio-recorded their response, transcribed it and then categorized the solution method they used.
Market maths word problem
We gave children a problem that was presented in a format that was familiar to school children but mimics the activity that working children do. Rounding could be used to simplify the cost of both goods. We did not allow pen and paper. The problem read: “Vishal went to the market with 200 rupees. He bought 450 grams of peas at 100 rupees a kilogram, and 200 grams of tomatoes at 90 rupees a kilogram. How much money does he have left?”.
Confidence treatments
In previous work, we found that children who performed well in arithmetic operations in the course of their job did not do well when solving standard arithmetic calculations when presented in a school-maths formulation. Two possible reasons for this are that children become stressed or lose confidence when they are presented with problems in a setting they are not familiar with. To test this hypothesis, we introduced two cross-randomized treatment variations. The first treatment varied whether oral abstract subtraction problems were presented before or after the hypothetical market maths problems. If abstract problems cause stress and stress impairs performance, then children who completed the abstract problems first will be more stressed while completing the abstract and hypothetical market maths problems and perform less well. The second treatment attempted to vary the level of self-confidence of the children by having the surveyor use more or less encouraging language during the survey. Specifically, we began by telling children we were interested in how children who work in markets ‘manage to be so exceptionally good at doing mental calculations’ versus ‘manage to do mental calculations in the course of their work, but often do poorly in school’.
Stress measures
As a first-stage measure for the confidence treatments, we measured children’s stress, confidence and attitudes to maths at the end of the survey.
Study 3a, wave 2
Sample
We returned to 34 out of the 38 markets we visited in study 3a, wave 1. We did not conduct a real market transaction with children in this study. However, we used a similar strategy to recruit children to ensure a comparable sample. As in previous studies, surveyors spent time observing children to determine whether they were handling transactions at their shop (calculating prices and providing change). If they appeared to be doing so, surveyors approached the child and enquired about the price of a good at a specific quantity. For example, asking ‘How much do 300 g of apples cost?’. If the child did not answer the question and had someone else in the shop answer on their behalf, we assumed that the child did not handle transactions and did not begin the survey with them. As a final check, we also directly asked children at the beginning of the survey whether they handled transactions and screened them out of the study if they did not. Of the 566 working children who were approached by one of our surveyors, 463 passed these screens, agreed to participate and completed the full survey.
Survey structure
Our survey consisted of the following sections: (1) consent; (2) simple arithmetic and confidence building; (3) hypothetical transaction; (4) warm-up abstract and anchored addition and multiplication arithmetic calculations; (5) oral abstract subtraction with anchoring hints; (6) oral abstract and anchored multiplication with rounding hints; (7) process hints; and (8) demographics.
Warm-up abstract and anchored addition and multiplication arithmetic operations
We asked children a series of oral addition and multiplication problems. Some of the problems were abstractly framed whereas others were anchored to a concrete context. This section served several purposes. First, it put children further at ease before they began the hint sections of the survey. Second, we randomized children into five groups who were given differing numbers of problems (ranging from two problems to six problems). This provided random variation for the position that questions appeared within the survey, which controlled for question order effects in our subsequent hint experiments. Finally, we compared performance on abstract and anchored problems. We randomized children into two versions of the test to exactly balance problem difficulty on abstract and anchored problems. We also provided a mix of roundable and non-roundable problems of similar difficulty.
Hint experiments
We include a detailed summary of the anchoring, rounding and process hint experiment methods in the Supplementary Methods (study 3a), with results in Extended Data Table 8, Extended Data Fig. 2 and Supplementary Tables 21, 22 and 25.
Study 3b
Identification of schools
We followed a similar sampling strategy to study 2b. We surveyed a total of 300 children, half in grade 7 and half in grade 8. All children we approached agreed to participate. Our main analysis focused on the 271 school children with no market-selling experience.
Survey structure
For study 3b, our survey consisted of the following sections: (1) consent; (2) ASER (as in studies 1 and 2; Supplementary Table 26); (3) written abstract, oral abstract and oral anchored assessment; (4) market maths word problem (as in study 3a, wave 1); (5) pretend market problem (as in study 3a, wave 1); and (6) market maths word problem with hints.
Written abstract, oral abstract and oral anchored assessment
We tested how school children’s arithmetic performance changed depending on how questions were delivered by asking questions in written abstract, oral abstract and oral anchored forms. For each of these sections, we tested children on one addition, subtraction, multiplication and division question. Other than the key feature, we balanced the complexity of the problems across these sections by randomizing children into one of four versions of the survey. For example, across the versions, children were tested on oral abstract and oral anchored problems with the exact same numbers. We also balanced the difficulty of roundable and non-roundable problems by ensuring they had similar numerical quantities and the same requirements to carry over numbers.
Pretend market transactions
We again set up a pretend market in children’s classrooms but made several changes relative to study 2 to test children’s performance in a setting that most closely parallels selling in a market. In particular, we designed the problem to be of comparable difficulty to the real-world market transactions, did not allow children to use pen and paper and required children to respond in 4 min or less.
Market maths word problem with hints
We tested whether providing a hint to use rounding strategies improves performance for non-working children, who may underutilize flexible arithmetic algorithms. There were two treatment groups: one received a hint to break down the problem; the other received a hint to both break down the problem and to use rounding strategies. Finally, the control group could re-attempt the problem without a hint.
Incentives
All children received tokens on the basis of whether they correctly answered the questions. We randomized whether children could exchange these tokens for non-financial gifts (incentives treatment) or whether children received a fixed gift (no incentives treatment).
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.