Central pattern generator control of a vertebrate ultradian sleep rhythm

Animals

Adult lizards (P. vitticeps) of either sex, weighing 150–300 g (around 1.5–3 years old), were obtained from our institute colony and selected for size, weight and health status. The lizards were housed in our state-of-the-art animal facility. All experimental procedures were approved by the relevant animal welfare authority (Regierungspräsidium Darmstadt, Germany) and conducted following the strict federal guidelines for the use and care of laboratory animals (permit nos. V54-19c20/15-F126/1005_1011 and F126/2006).

Lizard surgery for chronic recordings

Lizard surgery and electrode implantation was performed as described previously⁹. On the day before surgery, lizards were administered analgesics (butorphanol, 0.5 mg kg^−1 subcutaneously; meloxicam, 0.2 mg kg^−1 subcutaneously) and antibiotics (marbofloxacin, marbocyl, 2 mg kg^−1). On the day of surgery, anaesthesia was initiated with 5% isoflurane, and maintained with isoflurane (1–4 vol%) after intubation. Body temperature was maintained at 30 °C using a heating pad and an oesophageal temperature probe. Heart rate was monitored throughout the surgery using a Doppler flow detector. The skin covering the skull was disinfected using 10% povidone-iodine solution and subsequently removed with a scalpel. Cranial windows were cut to reach the claustrum bilaterally, dura and arachnoid were removed with fine forceps and scissors, and the pia overlaying the dorsal cortex was removed carefully to expose the site of electrode implantation. The exposed skull was covered with ultraviolet-hardening glue and stainless steel wires were secured subdurally to serve as reference and ground.

Silicon probes were mounted on Nanodrives (Cambridge Neurotech) and secured to the skull bilaterally using a stereotactic adaptor. The probes were slowly lowered into both claustra or adjacent anterior dorsal ventricular ridges on the day(s) following the surgery and to a final depth of 0.7–1.3 mm.

The brain was covered with sterile saline, followed by Duragel (Cambridge Neurotech) and Vaseline. The lizards were allowed to recover fully from anaesthesia on a heating pad set to 30 °C before being released into their home terraria.

In vivo electrophysiology

Before surgery, lizards were habituated for two to three nights to a sleep arena, which was itself placed in a 3 × 3 × 3 m³ electromagnetic-shielded experimental room. An infrared light source was placed on top of the arena and remained switched on for the entire duration of the experiment, allowing continuous monitoring of the animals’ behaviour and eye movements using infrared cameras. Around an hour before lights off, the lizards were placed into the arena and left to sleep and behave naturally overnight. They were returned to their home terraria the next day, when they received food and water. Experiments were performed at room temperature of around 21.5 °C. Lizards were entrained to a 12 h/12 h light/dark cycle (t_off = 18:00/19:00, winter/summer and t_on = 06:00/07:00, winter/summer). Light intensity during the artificial day, measured at the eye, was 15.5 lx (same intensity as for the light pulses).

Electrodes were either 32-channel silicon probes (catalogue no. ASSY-116 H7b, CambridgeNeurotech) and A1x32-Poly2-10mm-50s-177-H32_21mm (Neuronexus) or Neuropixel 1.0 probes. Experiments using 32-channel probes were performed using a Cheetah Digital Lynx SX system, and signals were sampled at 32 kHz. Neuropixel data were acquired nominally at 30 kHz using SpikeGLX software.

IronClust with manual curation was used for spike sorting (https://github.com/flatironinstitute/ironclust#readme) with MATLAB (MathWorks) v.R2021a and v.R2018a.

Electromyographic recordings

To quantify the difference in muscle tone of sleeping animals under light stimulation and awake animals, we estimated the integral of the electromyographic recording (EMG) (integrated EMG (iEMG), Extended Data Fig. 3) recorded in the animal’s neck. The EMG was recorded together with the LFP, sampled at 32 kHz using a Cheetah Digital Lynx SX system, and using a break-out wire (PFE-coated stainless steel Type-316, 125 µm bare) from a 32-channel silicon probe (catalogue no. ASSY-116 H7b, CambridgeNeurotech), insulated except at the tip and inserted into the neck muscle. We band-pass filtered (100–225 Hz) the signal, rectified it (absolute value) and calculated its time integral in a sliding window of 20 s (in steps of 1 ms).

Light-pulse experiments

Ambient light pulses were applied using LED lights (40 lx measured facing the bulb, 15.5 lx measured as from the eyes of the animal) located above the lizards’ sleeping arena and controlled via a USB-to-analogue interface sequence control v.2.0 connected to a personal computer. Pulse protocols started 2–3 h into the dark period, when animals were sleeping deeply and REM_P/SW periods alternated regularly (Fig. 1).

In all non-entrainment, single-pulse experiments during sleep (Figs. 1, 2 and 5 and Extended Data Fig. 4), light pulses were delivered between hours 2 and 10 of the recording (between around 20:00 and 04:00). We manually inspected and discarded the few instances in which the sleep rhythm preceding the light pulse was particularly irregular, because it affected our capacity to estimate the phase of the pulse. Hence, 9.15% (or 66 out of 721 in all) of the pulses (all durations) were excluded. No additional criteria (time of night, phase of the pulse or length of the cycle) was used for this selection.

Sleep entrainment

Light pulses of 1 s were applied at IPIs ranging from 80 to 240 s, 10–17 times in a row. The beginning of each pulse train was separated from the end of the preceding one by at least 30 min.

Awake entrainment

Experiments took place in the late morning or early afternoon, usually between 10:30 and 13:30, and thus several hours after awakening and during continuous exposure to light. Animals were upright and attentive, with an angled mirror facing the left eye and an infrared camera facing the other, such that movements could be monitored for both eyes (Supplementary Video 2). Each experimental session lasted 30–50 min, and consisted of alternating periods of ambient light OFF and ON (as described above), 9–13 times in a row, before the lights were kept OFF until the end of the experiment.

Monocular stimulation experiments

For monocular stimulation experiments, a black, three-dimensional printed plastic cup was secured to either left or right eye using silicon (Kwik-Sil). Eye cups were attached around 30 min before starting an overnight recording, and removed the following morning. To pool all unilateral cup experiments (Fig. 5), we use the colour red to indicate the side contralateral to the cupped eye (blind claustrum) and the colour blue to indicate the ipsilateral side to the cupped eye (seeing claustrum), independently of whether they correspond to true right or left.

Beta power and REM_P/SW detection

Note that the nomenclature (REM_P and SW) is descriptive, and does not necessarily imply, for lack of knowledge at this point, functional or mechanistic identity with mammalian sleep states.

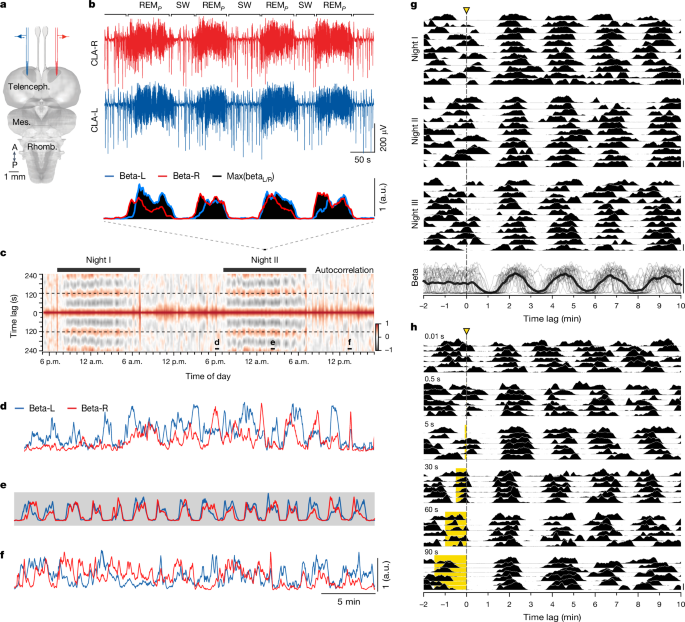
We extracted the power of the LFP signal in the beta band (12–30 Hz) for both hemispheres independently with a 10 s sliding window (in 1 s steps) using the Welch method^7,9. We then combined powers from both hemispheres by taking the maximum value of the beta power at any one time (Fig. 1b, bottom). To pool diverse recordings while accommodating for rare LFP artifacts, we normalized the beta power so that 0 corresponded to its bottom 5th percentile and 1 to its top 95th percentile. All scale bars for beta correspond to this 0–1 range. Because the timing of the light pulses did not always align with the 1 s sampling of the beta power, we resampled beta around the time of the pulse through linear interpolation with a period of 100 ms.

To define periods of REM_P and SW sleep, we took the log₁₀ of the combined beta and fitted a Gaussian mixture model to extract the two peaks of the resulting beta distribution. To avoid over-fragmentation resulting from the noisy crossing of this threshold, we ignored detours that left and re-entered the same state for a short duration (less than 15 s). We used the same method to determine REM_P-like and SW-like periods in awake experiments. However, awake experiments were much shorter because the animals generally tolerated only one round of light-pulse entrainment per session; the quality of the Gaussian mixture model fitting was thus reduced. Thus we instead selected thresholds of beta (0.2 for 60 s pulses and 0.4 for 90 s pulses) visually and allowed for shorter detours (less than 5 s).

For the summary in Fig. 5e, we used the above method to define SW (represented in grey) and coloured REM_P in blue or red to identify the claustrum that displayed the highest beta power at any one time. The side with highest beta power dominates the other (SNs are larger and occur 20 ms earlier than on the other side⁹).

To calculate the duration of the cycle, we calculated lagged auto-correlations of the combined beta and determined the lag within the range of 1–3 min that resulted in peak correlation.

To determine when the two hemispheres resynchronized (Fig. 5g), we defined periods of REM_P and SW on the combined beta as described above and determined the beginning of the first REM_P episode after the light pulse that followed a long period of SW (≥40 s).

Auto-correlations

To compute beta auto-correlations (Fig. 1 and Extended Data Figs. 1 and  3) we calculated Pearson’s correlation coefficient from our discrete signal (see ‘Beta power and REM_P/SW detection’ section). For lagged auto-correlations in Fig. 1 we used a sliding window of 20 min and 1 min steps. For Fig. 3 we use a 4 min window and 1 s steps. Formally,

where \(\beta (t)\) is the beta time series, \(w\) is the size of the window, \({\mu }_{{\beta }_{\tau }}\) and \({\mu }_{\beta }\) are the means of the lagged and non-lagged beta within the window, and \({\sigma }_{{\beta }_{\tau }}\) and \({\sigma }_{\beta }\) are the s.d. values within the window. The resulting value always falls in the range [−1, 1].

SN and SWR detection

We detected SNs and SWRs as described in ref. ⁹. In brief, for SNs, we low-pass filtered (40 Hz) the LFP and extracted its first and second derivatives. We then detected triplets of peaks corresponding to the start, middle and end of an SN. To remove false positives, we estimated the distribution of the noise and took only those SNs with a low probability (P < 0.025) in the noise distribution of amplitude and duration. For SWRs, we low-pass filtered (30 Hz) the LFP and detected negative peaks using the function scipy.find_peaks. We only considered peaks that were at least 500 ms from one another and that occurred within SW periods (see REM_P detection above).

Phase analyses and phase response curves

We extracted the phase of either combined (Figs. 2 and  3) or unilateral (Fig. 5 and Extended Data Fig. 6) beta-power (see ‘Beta power and REM_P/SW detection’ section) as described here. We first filtered the beta time series in the band 0.00277–0.16666 Hz using a Butterworth filter. This band preserves the range of timescales relevant to the beta cycle (0.00277 Hz = 6 min^−1, 0.16666 Hz = 1 min^−1). We then extracted the Hilbert transform, using the scipy.signal.hilbert function in Python. We next extracted the angle from the complex values of the analytic signal. This process would map the trough, peak and following trough of an ideal sine wave to −π, 0 and π, respectively. As the trough and peak of the band-pass filtered beta correspond to the middle of SW and REM_P, respectively, we phase-shift the angles by −π/2 to align −π and π to the beginning of REM_P. We then normalized the phase by mapping the range (−π, π] to (0, 1]. The resulting time series maps the beginning and end of SW sleep to 0 and 0.5 and the beginning and end of REM_P to 0.5 and 1. Owing to the properties of the Hilbert transform applied to the smoothened (band-passed) signal, this mapping of 0.5 to the transition of low to high beta remains true even when the duty cycle is not 50%.

Phase is a circular variable. We unwrapped this variable sequentially in Figs. 2e and 5b,c and Extended Data Fig. 6b. We used the function numpy.wrap in Python to detect large deltas that jump from 1 to 0 and added +1 from that point on. If applied to an ideal sine wave with no phase changes, the resulting series moves in a perfect monotonically increasing diagonal (similar to the averages in Fig. 5c and Extended Data Fig. 6b).

For the phase response curves (insets in Figs. 2e and 5b,c and Extended Data Fig. 6b), we calculated the difference of actual phase minus expected phase:

where \({\varphi }_{1}\) is the unrolled phase taken one natural period after the stimulus, and \({\varphi }_{0}\) is the phase at the time of the stimulus. The expected phase is the same as the phase of the pulse +1 due to the unwrapping. We obtained the duration of a natural period as described in ‘Beta power and REM_P/SW detection’ and took the actual phase value (\({\varphi }_{1}\)) from the unwrapped phase series. Because the Hilbert transform involves an integral from both directions in time, our estimation of the phase at which a light pulse fell (\({\varphi }_{0}\)) was influenced by the outcome of that pulse. To mitigate this effect, we always took the phase 5 s before the actual time of the pulse.

In Fig. 2d–f and Fig. 5b–e, we define the phase (\(\varphi \)) of the pulse as ‘early SW’ (blue) if \(\varphi \in [{\rm{0,0.25}})\), ‘late SW’ (green) if, \(\varphi \in [{\rm{0.25,0.5}})\) ‘early REM_P’ (orange) if \(\varphi \in [{\rm{0.5,0.75}})\), and ‘late REM_P’ (red) if \(\varphi \in [0.75,\,1)\), where \(\varphi =0\) is the onset of SW.

Tract tracing of retinal projections

The lizards were anaesthetized as described above (in vivo electrophysiology). Scales covering the skin above the eyeballs were removed carefully, and neurobiotin (20% dissolved in phosphate buffer) was injected intravitreally through a small incision using glass micropipettes, at a rate of 80–120 nl min^−1. Lizards recovered from anaesthesia on a heating pad and were subsequently returned to their home terraria. Ten days later, the animals were deeply anaesthetized with ketamine (60 mg kg^−1), midazolam (2 mg kg^−1) and isoflurane. After loss of the corneal reflex, the lizards were decapitated and their heads perfused with ice-cooled paraformaldehyde (4% in PBS). The brains were extracted and post-fixed with 4% paraformaldehyde–PBS for 24–48 h, and subsequently immersed in 30% sucrose for at least 48 h at 4 °C. Transverse sections were obtained at a thickness of 70 μm, using a cryostat, and neurobiotin was detected with streptavidin, Alexa Fluor 568.

Statistics

The data were processed using Python (v.3.11.5) and the standard Python packages numpy (v.1.24.3) and xarray (v.2023.6.0). Statistical tests were performed using the standard Python packages scipy (v.1.11.4) and pandas (v.2.0.3).

For the paired two-sided t-tests in Fig. 3e,f, we compared the median duration of REM_P (or SW) during the train of light pulses with their median duration in the preceding 25 min. For the Wilcoxon signed-rank paired two-sided tests and Mann–Whitney two-sided U-tests of Extended Data Fig. 3, we took the mean value of the iEMG (see ‘Electromyographic recordings’ section) in data segments of 6 min.

Detection of eye opening

To quantify eye openings in our awake experiments (Fig. 4f,g) and during sleep (Extended Data Fig. 3b), we used DeepLabCut (https://github.com/DeepLabCut) to track four points of each eye (midpoint of upper eyelid, midpoint of lower eyelid, left corner and right corner) from our continuous infrared camera recordings. We calculated the Euclidean distance in pixels between the upper and lower eyelids and then normalized them to their 5th and 95th quantiles. Note that, because our video recordings extended throughout each experiment, we tracked the eyes also before sleep started and after it ended, such that a value of 2 or more corresponded to a clear eye opening in awake animals. For Fig. 4g, we considered the eye to be open if this distance was above 0.25.

Data reporting

No statistical methods were used to predetermine sample size. The experiments were not randomized and the investigators were not blinded to allocation during experiments and outcome assessment.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.