Calving-driven fjord dynamics resolved by seafloor fibre sensing

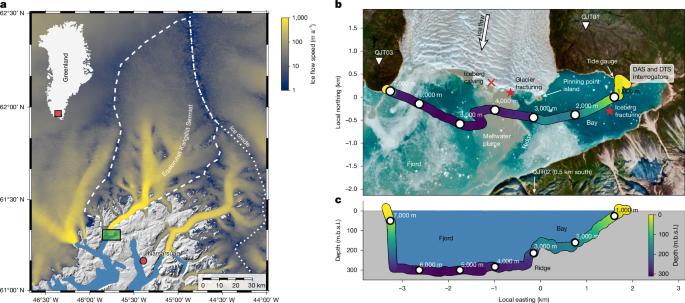
Study site

Eqalorutsit Kangilliit Sermiat (EKaS; also known as Qajuuttap Sermia) is, to our knowledge, the only major Greenlandic tidewater outlet glacier that has continuously gained mass over the past three decades⁵². At the calving front, the Eqalorutsit Kangilliit fjord is 280–300 m deep and filled with sediments, resulting in a flat bathymetry across the fjord. At the eastern part of the calving front, a pinning point bedrock island with about 100 m in diameter emerges from a subsea ridge that separates the deep fjord from a shallower bay (Fig. 1b). Calving at EKaS mainly consists of smaller collapses with infrequent rotational events as large as about 10⁶ m³. Between November and June, the fjord is usually covered with dense ice mélange near the calving front. Subglacial discharge is in summer of the order of 200 m³ s⁻¹ and is at times visible through the upwelling of turbid meltwater plumes at the calving front. Episodic outburst floods from subglacial and marginal lakes originate at the confluences of EKaS with its northwestern tributary glaciers.

Fibre-optic cable deployment

The deployed fibre-optic cable is a 10-km-long Universal Cable from the supplier NBG. It has a diameter of 4 mm and is armoured by 12 steel wire stands. Two single-mode (SM) and two multi-mode (MM) fibres are guided in a gel-filled steel tube. The cable has a mass of 40 g m⁻¹ (3,200 kg m⁻³ density) and was spooled onto a wooden cable drum with a total weight of 500 kg. We deployed the cable by hand from the stern of the ice-strengthened vessel Adolf Jensen (Extended Data Fig. 1a,b) and synchronized the cable output with the travelled GNSS track distance. Cable sections in shallow water near the eastern shore were deployed from a small, motorized landing boat. The 250-m-long cable section on land leading to the interrogators was trenched in about 20 cm depth. By contrast, the entire 7-km-long submarine cable section was deployed without trenching, by letting the cable sink to the seafloor.

A strong optical loss in both SM fibres at approximately 960 m OD along the cable occurred already during the cable deployment (Extended Data Fig. 2b), forcing us to operate our DAS measurements atypically on one of the two MM fibres. These only experienced a co-located loss of 3 dB. During our 3-week-long fibre-optic measurements, the cable suffered multiple damages. From 10 August 05:41 UTC and 17 August 04:40 UTC onwards, we were not able to measure any backscattered light from farther than 5,435 m and 4,135 m OD, respectively, which effectively shortened our cable to terminate at the centre of the calving front eventually. From 10 August 12:10 UTC onwards, a substantial 3.5 dB loss in the MM fibre was present at 681 m OD. We attribute these losses, on one hand, to kinks in the fibre-optic cable formed by seafloor currents dragging the cable and tightening loops that formed from too much slack. On the other hand, we attribute the losses to bends in the fibre because of icebergs becoming stranded on the cable in the shallow bay waters during low tide.

DAS interrogator setup

We deployed a Sintela ONYX v.1.0 interrogator for DAS at the northern shore of the bay east of the calving front (Fig. 1b). The interrogator was situated in a waterproof aluminium box together with 12× Yuasa 65 Ah 12 V gel batteries powered by 4 × 300 Wp Goal Zero Ranger solar panels (Extended Data Fig. 1c). We continuously recorded strain along one of the two available MM fibres in our cable at 2 kHz sampling rate, 4.79 m gauge length and identical channel spacing between 9 and 29 August (1,587 initial seismo-acoustic sensing sections). A data gap occurred between 20 August 13:55 UTC and 21 August 13:00 UTC (23 h) because of an unexpected laser shutdown of the interrogator that was detected only a day later during maintenance. While recording, we additionally saved directly downsampled data at 100 Hz, 10 Hz and 1 Hz sampling rates, creating a dataset of 13 TB in total. Each time the effective cable length diminished, we adjusted the interrogator settings to record only the functional cable length.

DTS interrogator setup

Co-located with the DAS interrogator, we deployed a Silixa XT-DTS M interrogator for DTS. Similar to the DAS setup, the interrogator was situated in a waterproof aluminium box with 6× Yuasa 65 Ah 12 V gel batteries powered by 1 × 300 W Goal Zero Ranger and multiple smaller solar panels (33–68 W) mounted around the box for stand-alone operation (Extended Data Fig. 1c). We operated the DTS in single-ended configuration on one of the two MM fibres with a channel spacing of 25 cm and an integration time of 5 min (34,448 initial sensing sections). As a first temperature reference, we spooled up 25 m of cable inside a styrofoam box that was placed inside the larger aluminium box on top of the batteries. As a second temperature reference, we spooled up 25 m of cable inside another insulated box and buried it at 50 cm depth in the soil. Both temperature reference sections were equipped with a PT100 thermometer directly connected to the DTS interrogator. Moreover, we used an RBRduet³ temperature and pressure sensor at the eastern cable landing location to measure near-surface water temperature. On the west shore, we spooled up the remaining cable and put it into an insulated aluminium box together with a Geoprecision M-Log 5 W temperature logger. As for the DAS setup, we adjusted the DTS interrogator settings each time the effective cable length diminished.

Additional instrumentation

In July 2022, we installed three Nanometrics Trillium Compact broadband seismometers with a flat response between 120 s and 100 Hz on the hilltops east, south and west (QJT01, QJT02 and QJT03) of the calving front of EKaS and sampled them at 200 Hz. Owing to fox bite damage, the sensors were only running continuously from 2 August 2023 12:25 UTC (QJT03), 11 August 2023 17:20 UTC (QJT01) and 14 August 2023 17:20 UTC (QJT02). On 5 August, we measured 22 vertical CTD (conductivity, temperature and depth) profiles with an RBRconcerto³ profiler from the R/V Adolf Jensen along the fibre-optic cable deployment route parallel to the calving front. A weather station (Decagon) co-located with the interrogators collected air temperature, solar irradiation, precipitation and relative humidity in 10-min intervals starting from summer 2022. For the first days of our fibre-optic measurements until 15 August, a terrestrial radar interferometer (Gamma Portable Radar Interferometer, TRI) situated on the hill south of the calving front was scanning the calving front of EKaS in 1-min intervals and monitoring ice-flow speed and calving activity (timing, volume and locations)⁵³. A time-lapse camera co-located with the radar took images of the calving front in 2-min intervals until 15 August, and in 20-min intervals subsequently. Where the fibre-optic cable enters the bay, a combined temperature and pressure sensor (RBRduet³) recorded tides, wave heights and surface water temperature at a 3-s interval.

DTS calibration

We use the Python package dtscalibration (ref. ⁵⁴) for calibration of the raw Raman Stokes and anti-Stokes backscattering recordings from the Silixa XT-DTS M. We corrected for the optical losses in the fibre that occurred during the deployment, by applying a correction factor to fibre sections after the loss such that the corrected Stokes and anti-Stokes intensity in a 30-m region around the optical loss is linear. The 3.5-dB loss that occurred on 10 August 12:10 UTC altered the recorded backscattered light for multiple tens of metres nonlinearly. We corrected for this particular optical loss by multiplying all measurements and fibre sections before and after the loss by the ratio of the last measurement before and the first measurement after the loss occurred, assuming only small fluctuations in temperature over the 5-min measurement interval. This procedure results in Stokes and anti-Stokes data, as would be expected without optical losses along the fibre.

After this preprocessing, we followed a single-ended calibration procedure in ref. ⁵⁴ to derive the differential loss Δα along the fibre, the sensitivity of the Stokes and anti-Stokes scattering to temperature γ, which depends on the fibre material, and a lumped factor C accounting for sensitivity of the detector, the number of molecules involved in scattering and the wavelength dependency backscattered light. The temperature for each fibre section is then obtained with the measured Stokes P_S and anti-Stokes P_AS intensity by

We solve for γ and Δα by fitting the DTS temperatures at reference sections (1) inside an insulated box within the aluminium box that houses the interrogator; (2) inside an insulated box 50 cm deep in the soil; and (3) a cable coil in shallow water at the shore with co-located temperature probes. Furthermore, we require the cable sections close to the shore east and west of the fjord to match while the full fibre-optic cable length is operational. We then calibrate the temperature for the entire 3-week-long measurement with fixed γ and Δα values. Residuals of the calibration are shown in Extended Data Fig. 11.

DAS phase to strain conversion

We convert raw phase ΔΦ (units of radians) recordings of the Sintela ONYX interrogator to units of strain using

with the vacuum wavelength of the laser λ = 1,550.12 nm, the effective refractive index of the fibre n_eff = 1.4682, the gauge length x_g = 4.79 m, and the strain-optic coefficient ψ = 0.78. The internal data flow of the interrogator applies a leaky frequency filter at 0.1 Hz. For frequencies ≲10 mHz, this filter acts as a differentiator, which results in phase measurements proportional to strain rate, instead of strain. Therefore, we show the DAS data in units of strain, raw phase record or normalized per channel, depending on the frequency of interest.

DAS temperature response

In the DAS recordings, a temperature increase at a given segment of the fibre-optic cable will become evident as a positive strain-rate signal (red in Figs. 5c,d and 6b,d). This signal has two origins: (1) the thermal expansion of the fibre-optic cable with increasing temperature; and (2) the increase of the refractive index with temperature will be sensed by a positive phase change:

with the thermal expansion coefficient α_T = 5 × 10⁻⁷ K⁻¹, the thermo-optic coefficient ξ = 6.8 × 10⁻⁶ K⁻¹ (ref. ⁵⁵). As for frequencies ≲10 mHz, our DAS recordings are proportional to strain rate (see previous section), our interrogator’s response is then about \(\Delta \phi =\,\frac113\times 1^-3(\rmK\,s^-1)\times \frac\rmdT\rmdt(\rmK\,s^-1)\), meaning that a temperature change by 13 mK s⁻¹ will result in a 1 rad signal. Δϕ ≳ 100 over less than a minute caused by the seafloor temperature drops associated with internal wave wakes resulted in faulty phase unwrapping and, therefore, subsequently wrong phase measurements⁵⁶ (Fig. 6b,d). For the maximum seafloor temperature drop of 0.8 K over less than 100 s (interrogator response is proportional to strain), the expected phase change would be Δϕ ≈ 330.

Cable location

We expect the cable to sink to the seafloor in about 15 min. The cable sinking speed is approximately determined from the force balance between the drag force per unit length

acting on the cable during sinking with the density of water ρ_water, the sinking velocity v, the drag coefficient c_d = 1.0, the cable diameter d = 4 mm and the gravitational force on the cable

with the gravitational acceleration g, and the mass density per unit cable length m_cable = 0.04 kg m⁻¹, resulting in a sinking speed of v ≈ 0.4 m s⁻¹. Currents in the fjord are expected to be strongest at the water surface and up to 1 m s⁻¹ (ref. ⁵⁷). We, therefore, expect the cable to not be farther off the vessel deployment track than a few hundred metres in the deep fjord sections and virtually underneath the vessel track to within a couple of ten metres in the bay in which strong surface currents are absent.

To further constrain the location of individual cable sections in the deep fjord (Extended Data Fig. 2a), we pick the Scholte wave arrivals from a calving event at 10 August 01:30:45 UTC (Fig. 3d) with a short-term-average/long-term-average (STA/LTA) trigger of 1 s/10 s in the data band-passed filtered between 1 Hz and 10 Hz (Extended Data Fig. 10a). The TRI located the origin of the tsunami caused by this event at 61.310, −45.783 (latitude, longitude; Extended Data Fig. 10c). From the picked arrival times and the event location, we then run a Bayesian inversion using a Markov-chain Monte-Carlo algorithm for locating individual cable sections in the deep fjord section of our fibre-optic cable installation⁵⁸. Therefore, we follow the steps below:

1. 1.

   We pick the calving front location at 40 points from Sentinel 2 imagery and interpolate linearly between the picks to get a continuous one-dimensional function of the calving front location (longitude as a function of latitude).

2. 2.

   Interpolate the cable deployment track west of the pinning point island, resulting in a coordinate for every DAS channel and consecutively resample this curve to only 11 anchor points—one at the west shore, one where the cable enters the deep fjord and nine equally spaced (OD) in between. These nine anchor points (x, y) will be what we will invert for later (2 × 9 = 18 parameters). We leave the boundary anchor points to be fixed, as we know the location at the west shore, and we assume that the cable sits directly below the deployment track in the bay.

3. 3.

   Our observations are the relative arrival times of the Scholte wave at the cable, which we automatically picked from the DAS data (Extended Data Fig. 10a).

4. 4.

   Our model (M) calculates the two-dimensional travel time between the calving event location and the DAS channel coordinates for a given velocity.

5. 5.

   We define a prior for our Bayesian inversion, assigning an a priori probability to the parameters that we will invert for and which are the 9 anchor points with x and y coordinates each (x_n, y_n), a Scholte wave velocity v, the East–West coordinate of the calving event location dx (North–South coordinate is derived from the shape of the calving front in (1)), and an absolute time offset dt for when calving event happened p(x_n, y_n, v, dx, dt). We assign a zero probability to the set of inverted parameters if the Euclidean distance between the anchor points is larger than the OD along the cable. We further assign a Gaussian probability distribution to the anchor point locations with a width of 1,000 m and centred around the initial position from the cable deployment track. Last, we allow for small shifts of the calving event location and assign it a Gaussian weighting with a width of 100 m around the radar-derived calving location.

6. 6.

   For calculating the likelihood of the chosen parameters (anchor points, Scholte wave velocity, calving event location and event time), we do a cubic interpolation of the anchor points, resulting in a location for each channel. We then run the arrival time model for the chosen parameters and define the likelihood as the absolute difference between the modelled and the picked arrival times p(t_k|x, y, x_n, y_n, v, dx, dt), with arrival times t_k and the interpolated locations for each DAS channel x, y.

7. 7.

   We calculate the logarithmic posterior probability as the sum of the logarithmic prior and the logarithmic likelihood

   $$p(x_n,y_n,v,\rmdx,\rmdt| t_k)\propto p(x_n,y_n,v,\rmdx,\rmdt)\,p(t_k| x,y,x_n,y_n,v,\rmdx,\rmdt).$$

   (6)

8. 8.

   We now initialize a Markov-chain Monte-Carlo sampler with 64 walkers for each inversion parameter, randomly distributed around the initial cable location using the affine invariant Markov-chain Monte-Carlo (MCMC) ensemble sampler emcee⁵⁷ for maximizing the logarithmic probability function from (6). We run the MCMC for 50,000 steps while checking for convergence. We select only the last 10,000 steps, resulting in a posterior probability distribution estimate of the parameters we inverted for—in particular, for our nine free anchor points.

9. 9.

   We again do a cubic spline interpolation between the nine free and two constrained anchor points to retrieve a cable geometry for each accepted inversion. From this cable geometry set, we calculate the median and the standard deviation, corresponding to the most likely cable layout given the calving event picks as well as the Scholte wave speed (Extended Data Fig. 10a,b).

An accurate assignment of absolute depths to cable sections leading from the submarine ridge between the fjord and the bay down into the deep fjord was unsuccessful. An attempt to match DTS recordings on cable sections between 2,820 m and 3,150 m OD from 9 to 10 August to the CTD temperature profiles close to the ridge from 6 August resulted in an unphysical cable layout with depth differences between adjacent DTS channels larger than the channel spacing of 25 cm. The reason for this discrepancy is probably the daily temperature variability of up to 0.5 K for a given depth as well as the long-term variability of several 100 mK day⁻¹ that impedes a direct comparison of the DTS and the non-simultaneously recorded CTD profiles (Extended Data Fig. 5).

Locating fracturing and detachment events

Our cable layout along the calving front spans an approximately linear array of sensors. For such a linear array, hyperbolic-shaped first wave arrivals are expected from point sources (see section 7.4.2 of ref. ⁵⁹). In the case of a perfectly linear array, the point source origin is ambiguous and can be located on a plane that is perpendicular to the linear array. Our imperfectly linear cable layout resolves this ambiguity, allowing for event location in three dimensions. For locating both iceberg detachment and fracturing events, we fit synthetic travel time curves to the wave arrivals of the recorded DAS signal (Fig. 3a,b,d). In the case of acoustic arrivals from glacier and iceberg fracturing events, we assume a constant three-dimensional wave speed of 1,500 m s⁻¹ in water, and locate the event origin for the shown events at the ice front, the bay and the fjord (Figs. 1b and 3a,b and Extended Data Fig. 2a). In the case of Scholte wave arrivals from iceberg detachments, we assume a two-dimensional propagation along the water–sediment interface with an unknown constant wave speed. We then invert simultaneously for the event location and the wave speed, identifying the wavefield origin at the calving front (Fig. 3d and Extended Data Fig. 2a).

Detachment event sensitivity estimate

The interferometrically derived subaerial calving volume integrated over 10 min from the TRI does not fully resolve the single calving events observed with DAS, thus hampering an unambiguous assignment of calving volumes to DAS observations. As a result, a TRI-derived calving-volume catalogue comprises 133 events in 10 days, compared to about 30,000 events observed with DAS over a similar 10-day time span (observational times do not fully overlap). Calving is expected to represent a self-organized criticality, in which the calving event rate R follows a power-law relationship with calving event volume R ∝ V^−b (refs. ^18,60) and, therefore, allows us to estimate a detection threshold for our subsea DAS. An exponent b = 0.79 ± 0.06 fits our TRI-derived calving volume number statistics, indicating that large calving events dominate mass loss (exponent <1). Extrapolating the cumulative volume number statistics from the TRI catalogue to the 200-fold event rate, we derive the calving event detection threshold of our DAS recordings as about 100 m³, much below the TRI threshold of about 5,000 m³ (Extended Data Fig. 4). The expected total calving volume observed with DAS then calculates to be around 40% larger than the total volume observed with TRI, because of the TRI missing small events. Comparing the ice flow based on a satellite-derived mean ice-flow velocity across the calving front of 4.5 m day⁻¹, a front width of approximately 3,500 m and an average height of about 80 m, and accounting for changes in the front position, the TRI detects only around 35% of the actual calved-off ice volume. However, owing to smoothing, 50% of the measured volume may get lost in the TRI detection process, increasing the TRI sensitivity up to about 70% of the actual calved-off volume. Now, considering the estimated cumulative calving volume detected with DAS is 40% larger than with the TRI, this means that DAS may detect up to about 98% of all solid frontal ablation. Note that, unlike the TRI, DAS is also able to detect submarine calving events.

Calving location from tsunami dispersion

Calving-induced tsunamis propagate as linear SGWs. We apply a frequency–wavenumber (f–k) transform to the DAS data (Fig. 4b) and find good agreement between the observed f–k energy distribution and the SGW dispersion relation

with angular frequency ω, wavenumber k, gravitational acceleration g and water depth h (ref. ⁶¹). We dominantly observe eastward tsunami propagation (that is, energy with positive wavenumber). The tsunamis mainly occur in the SGW deep-water limit (h > 0.5λ), where the group velocity

is independent of water depth. In the 300-m-deep fjord, this relation holds for wave numbers k > 0.01 m⁻¹.

Calving event spectrograms (Fig. 4c) show the arrival of low-frequency energy (about 30 s period) approximately 2 min earlier than higher-frequency energy (around 10 s period). By relating the rate of frequency shift to the distance D of the wavefield origin⁶²,

and fitting it to the spectrogram, we locate the calving event that caused the recorded tsunami 750 m west of the pinning point island, which agrees with TRI backscatter imagery (latitude, longitude: 61.3088, −45.7740; Fig. 4d,e). From this location, we simulate the tsunami arrivals in Fig. 4a using the Python package pykonal⁶³ based on the bathymetry and the general formula for the group velocity at 30 mHz:

Fjord stratification stability analysis

Cold and fresh water overlying warm and salty water, as we observe, are preconditions for convective salt and heat transporting processes. The Turner angle

is a measure of the strength of the convection process^42,64.

is the density ratio with the thermal expansion coefficient α, the haline contraction coefficient β and the vertical temperature and salinity gradients \(\frac\partial T\partial z\) and \(\frac\partial S\partial z\). Turner angles of T_u = 50 ± 6° (Extended Data Fig. 6a), calculated from our CTD casts, show that weak diffusive convection is present, particularly below the subglacial discharge intrusion at about 100 m depth, explaining the staircase pattern that we observe in the CTD casts (Extended Data Fig. 5).

IGW analysis

We observe a typical triangular pattern with reversing polarity in the DAS records as propagating IGWs impinge on the steeply sloping seafloor cable (Fig. 5d). IGW frequencies of about 0.5–1.0 mHz (15–30 min period) are close to and slightly below the buoyancy frequency N, calculated from CTD casts (Extended Data Fig. 6b), representing the free oscillation mode of a stratified fluid (see equation 2.243 of ref. ⁶⁵),

with reference fluid density ρ₀ and density gradient \(\partial \rho (z)/\partial z\) with depth z. The mean buoyancy frequency below 150 m depth calculated from the CTD profiles is N = 1.4 ± 0.4 mHz with a peak of N = 2.3 mHz at 193 m depth, at which a thermohaline step is located. With DAS and DTS, we predominantly measure the vertical displacement of the thermohaline steps. Along with the simplified IGW dispersion relation

observed IGW frequencies ω < 0.5N at the thermohaline steps imply θ > 60° with the vertical, and thus we can determine predominantly horizontal wave propagation. During the passage of an internal wave, the temperature change ΔT(z) at a given depth z is assumed to be adiabatic, with variations only due to heaving of isotherms (vertical advection),

with vertical displacement w(z). For our thermohaline staircase, we observe salinity to scale linearly with temperature, and to dominate the water density (Extended Data Fig. 7b), implying that the IGW signal measured with DTS and DAS will be strongest at temperature steps.

DAS sensitivity to internal waves

The 5-min sampling of our DTS just barely samples the IGWs with a 15–30 min periodicity. Vastly improved resolution is offered by our DAS data with its 2 kHz sampling rate. For frequencies lower than 10 mHz, as is the case for the internal waves, our DAS phase recordings are proportional to strain rate (see previous sections). IGWs become evident by the vertical displacement of the temperature steps (Fig. 5b), as well as the horizontal propagation of IGWs along the cable (Fig. 5d). An upward heaving of the thermohaline staircase (increasing temperature at fixed depth) will be recorded as a positive strain rate, a downward motion as a negative strain rate⁵⁵. The DAS record of IGWs, therefore, allows an independent measurement of the thermocline evolution that does not suffer from an absolute temperature calibration as the DTS record requires. As DAS accurately resolves the IGW frequency, which we observe to be close to the buoyancy frequency, temporal variations in the density gradient can be resolved.

Calving-induced submarine melt

We calculate the submarine melt rate at the calving front due to turbulent heat transfer from calving-induced IGWs following the commonly used three-equation model⁴⁴. The first equation relates the freezing temperature in the boundary layer T_b along the ice–ocean interface to salinity S_b and pressure p_b

with empirical coefficients a = −5.73 × 10⁻² °C psu⁻¹, b = 9.39 × 10⁻² °C and c = −7.53 × 10⁻⁸ °C Pa⁻¹ (ref. ⁴⁴). The second equation is the heat balance at the interface

with the melt rate \(\dotm\), the density of ice ρ_i and water ρ_w, the specific heat capacities of ice c_i and water c_w, the drag coefficient C_D = 0.01, the turbulent transfer coefficient for heat Γ_T = 0.01, the absolute ice-parallel speed outside of the boundary layer |u|, the ice temperature T_i, and the water temperature outside of the boundary layer T (measured by DTS). The third equation is the salt balance at the interface

with the turbulent transfer coefficient for salt Γ_S = 3 × 10⁻⁴, and the salinity outside the boundary layer S (ref. ⁶⁶).

We solve the three equations for the melt rate by using the linear relationship between the temperature and salinity from the CTD casts S = 0.5 psu °C⁻¹ × T + 32.6 psu (Extended Data Fig. 7b) and assuming that the ice temperature equals the boundary layer temperature T_i = T_b, and meaning that all available heat is used for melting, which introduces only a minor uncertainty. From the DTS data, we calculate vertical water velocities at the fibre-optic cable and assume these to be identical adjacent to the ice. With these, we calculate melt rates of up to 1.3 cm during a 3-h-long IGW wave train (0.07 mm min⁻¹) and peak values of up to 0.2 mm min⁻¹ (Extended Data Fig. 9). For IGW with amplitudes comparable to the water depth, we expect the horizontal flow component to contribute equally to the melt rate. Appreciating the effects of surface roughness, turbulence induced by released air bubbles from melted glacier ice, as well as the uncertainty in the turbulent heat transfer, and underestimations in the velocity field derived from the DTS data due to the finite temperature resolution, we expect melt rates of more than 1 mm min⁻¹ (refs. ^67,68,69).

Calculating seafloor currents from vortex-induced vibrations

During the passage of IGW wakes⁷⁰, we observe harmonic oscillations of the cable typically coherent over 20–50 m and strain signals about 10 times higher than for the rest of the cable. Two different types of vibrational modes with a distinct spectral signature are present. The first type constitutes tension-dominated cable modes with closely spaced frequencies (grey lines in Fig. 6f) following a linear sequence, with the nth harmonic frequency following

with the suspended cable length L, the horizontal tension in the cable T and the cable mass per unit length m = 0.04 kg m⁻¹ (refs. ^46,71). These first-kind cable modes are associated with lock-in vortex-induced vibrations (VIVs), establishing the natural frequencies of the suspended cable section.

The second mode type is characterized by widely spaced frequencies, also following a linear sequence f_k ∝ k. They result from multiple lock-in harmonics f_n, excited sequentially as the lock-out VIV frequencies

pass each of the lock-in frequencies f_n. Here \(v_\perp \) is the ocean current speed normal to the cable axis, St ≈ 0.2, the Strouhal number describing the flow regime, and the cable diameter d = 4 mm. From the lock-out frequencies f_k, we determine the ocean current speed perpendicular to the cable (along the fjord) (Fig. 6e,f). During IGW wake passage, the fundamental mode lock-out VIVs (k = 1) at the flanks of the wake range between about 2 Hz and 12 Hz (region between dashed white lines in Fig. 6f), which translates to seafloor current speed between 0.05 m s⁻¹ and 0.2 m s⁻¹. Lock-in frequencies, in turn, vary only slightly over time (fundamental mode: about 2.5 Hz in Fig. 6f), as with increasing current, the cable tension T increases, on which the lock-in frequency f_n is only weakly dependent \(f_n\propto \sqrtT\) (ref. ⁷²).