Broadband transient full-Stokes luminescence spectroscopy

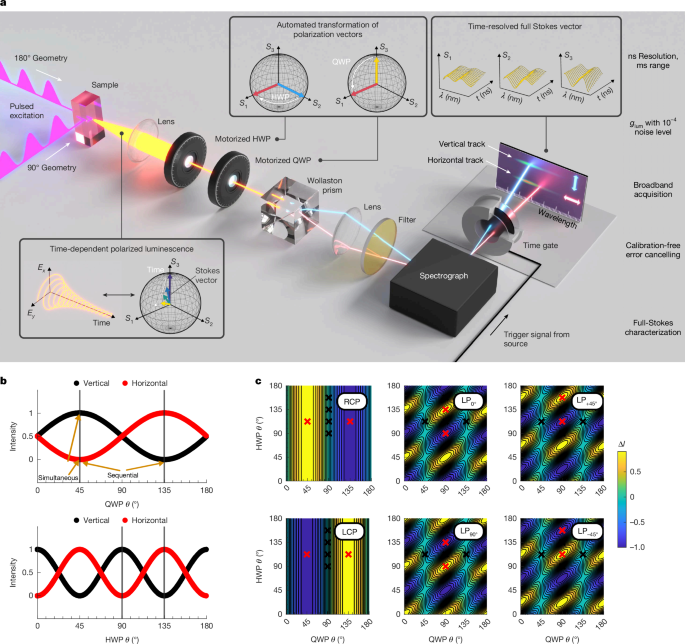
Separation of polarization components of sample luminescence

A schematic of the setup with specifications and part numbers of the main components are provided in Supplementary Fig. 1 and Supplementary Information section 1.1.

Sample luminescence is collected by a lens and passed through a set of polarization optics consisting of a superachromatic HWP, a superachromatic QWP and a 1° Wollaston prism. The HWP and QWP are placed in motorized rotation mounts, whereas the Wollaston prism remains fixed. After the polarization optics, the luminescence is focused onto a (vertical) spectrograph slit by a lens. The result is a free-space configuration with no fibre coupling or mirrors between the sample and spectrograph.

Polarization tracks are spatially separated (vertically) from the single luminescence beam by the fixed Wollaston prism. Therefore, one track will always correspond to a vertical polarization and the other to a horizontal polarization (which we will call horizontal and vertical tracks accordingly). Tracks are passed to a grating and focused onto an intensified CCD 2D-array detector (ICCD).

An illustration of how the various Stokes components produce intensity differences between the tracks in the ideal case with both a HWP and QWP present is presented in Fig. 1c. Waveplate orientations are defined about the fast axis relative to the table plane. Rotation of waveplates results in projecting the luminescence polarization components of interest (0°/90°, +45°/−45°, LCP/RCP for S₁, S₂ and S₃, respectively) onto the horizontal or vertical tracks. The other waveplate orientation (varied by 45°/90° from the first for the HWP/QWP, respectively) is then used to swap the polarization components between the tracks. This combination of simultaneous (orthogonal polarizations measured at the same time on different tracks) and sequential (orthogonal polarizations measured on the same track after waveplate rotation) measurements allows for cancellation of major errors due to different transmissions along the two beam paths and time instability as previously described³¹.

We note that it is in principle possible to only use an HWP for conducting an S₁/S₂-only measurement and to only use a QWP for an S₃-only measurement. Yet, for a faster, fully automatable full-Stokes measurement, it is advantageous to have both waveplates in place for all measurements. In all cases, the waveplate angles for measuring a given S_n component are such that the other two components are split evenly across the two channels and, therefore, are not measured as a false polarization signal in the ideal case. Importantly, for CPL measurements, the HWP orientation in principle does not matter, but in all orientations, the HWP will act to transform LCP to RCP and vice versa, which must be accounted for in processing.

Imperfections in real-life optics can produce polarization artefacts, including the well-known false CPL signals when substantial linear polarization is present¹⁸. It is, therefore, advisable in polarization measurements to take care when interpreting small polarization components in the presence of other, larger polarization components.

Excitation/collection geometry and excitation polarization

Sample excitation is possible in various configurations, defined by the relative angle and polarization of the excitation beam with respect to the collection optics. In general, artefact-free CPL measurements are possible in two configurations: (1) with 90° excitation/collection geometry and horizontal excitation polarization or (2) with 180° excitation/collection and unpolarized excitation polarization¹⁹.

All data presented in this work were collected from solution samples, for which the 90° excitation/collection geometry with square-based four-window cuvettes was found to be the most straightforward approach (more details in Supplementary Information section 4.1). In this geometry, photoselection effects in collected luminescence (affecting the degree of induced linear polarization) can be minimized by using a horizontal excitation polarization and maximized by a vertical excitation polarization.

Horizontally polarized excitation was used for artefact-free CPL measurements. Vertically polarized excitation was used to intentionally induce photoselection and linear components in luminescence.

Excitation beam polarization states were set using a HWP and linear polarizer after the excitation light source.

Sample preparation and measurement conditions

Eu[(+)-facam]₃ was used as received from the supplier (Sigma-Aldrich). Rhodamine B was used as received from the supplier (Radiant Dyes). (R/S)-BINOL-phthalonitrile-tBuCz was synthesized according to previously described methods⁴⁷.

Solution concentrations were 0.5 mM (non-polarization-resolved measurements) and 11 mM (polarization-resolved measurements) for Eu[(+)-facam]₃ in DMSO, 0.6 mM for (R/S)-BINOL-phthalonitrile-tBuCz in toluene, 37 μM for rhodamine B in water, 33 μM for rhodamine B in a water:sucrose mixture.

Solution samples were prepared using anhydrous solvents in a nitrogen-filled glovebox, except for aqueous solutions of rhodamine B, which were prepared under ambient conditions. Aqueous solutions were prepared using distilled water. For high-viscosity solutions, sucrose was dissolved in water near the solubility limit (approx. 2 g ml⁻¹). The Eu[(+)-facam]₃ solution in ‘wet’ DMSO was prepared by adding 0.5% v/v deionized water to the 11 mM Eu[(+)-facam]₃ solution, in which the solution was measured 5 h after the addition of water, similar to the methodology described in ref. ¹⁶.

Solutions were placed in screw-top four-windowed quartz cuvettes with a 1-cm square base. Air ingress to cuvettes was reduced by further sealing with PTFE tape and parafilm within the glovebox, where appropriate. Solutions were measured at ambient temperature in a laboratory with controlled and monitored temperature, recorded as 21 ± 0.3 °C for all measurements.

Sample excitation

For time-resolved measurements, samples were optically excited using the output of a Light Conversion PHAROS laser (Yb:KGW lasing medium, 1,030 nm, pulse energy 400 μJ, pulse width duration 200 fs and repetition rate of 50 kHz). The pump beam was generated from the seed in a harmonic generation unit (Light Conversion HIRO) by nonlinear crystals (beta-barium borate and lithium triborate) with residual fundamental removed by dichroic mirrors within the unit. Second and third harmonics can be generated, giving pump wavelengths of 515 nm or 343 nm, respectively. Other excitation wavelengths were generated using an optical parametric amplifier (Light Conversion ORPHEUS-NEO). Pump pulse energy at the sample was 10–70 nJ, with the pump focused down to a beam diameter of approximately 1 mm on the sample. The laser repetition rate is controllable by a pulse picker, and repetition rates in the range of 0.5–50 kHz were used as specified, where data are presented.

For continuous wave excitation at 405 nm, a laser diode (ThorLabs DL5146-101S mounted in a ThorLabs LDM9T temperature-controlled mount) was used, with a constant output power of 5–50 mW.

Signal collection and time ranges

The ICCD sensor has 2,048 × 512 pixels, enabling simultaneous recording of multiple tracks. Horizontal and vertical polarization components, spatially separated (on the vertical axis) by a Wollaston prism, are simultaneously recorded. The spectrograph grating splits the wavelengths in both tracks horizontally across the sensor. Vertical pixel binning is used to produce two effective vertical pixels for each wavelength pixel, giving I_h(λ) and I_v(λ) for the horizontal and vertical channels, respectively.

The intensifier of the ICCD only passes through a signal when a gate pulse is applied across it. Setting gate pulse values allows for adjusting the time over which luminescence is measured. For time-resolved measurements, the quantities recorded during a single acquisition are I_h(λ, t) and I_v(λ, t), where t is defined by the gate pulse applied. Time series are built up by repeating the measurement with modified gate delays and widths.

Accessible time bins range from approximately 2 ns to 2 ms for the described setup, with the lower limit arising from the intensifier specifications. The upper limit is practically limited by the laser repetition rate, as very long gate pulse values are achievable. In our setup, the laser operates at 50 kHz and can be pulse-picked for a lower frequency operation at the same per-pulse fluence (and lower time-averaged power). The practical limit for sufficient luminescence for measurements was found to be approximately 500 Hz, corresponding to a maximum time range of 2 ms; extending this would be reasonably straightforward by increasing per-pulse power at the sample, in principle.

For time-averaged values, comparable to steady-state measurements, a bin size spanning the entire time period between excitation pulses (or at least the time period during which luminescence is present) can be used with a pulsed excitation. Alternatively, the setup can be switched to a continuous wave excitation source, in which case only a time-averaged value is measured regardless of detector time gating.

Data processing

Error cancellation and changing the Stokes polarization component measured require repeating the measurement with rotated waveplates. Subsequent data processing to remove dark background signals and obtain error-corrected polarization spectra and related quantities was carried out with simple scripts. Algorithms for measurement automation are presented in Supplementary Information section 5.

To denote the orientations of the HWP and QWP, we will call the recorded intensities I_{v,QWPθ,HWPθ} and I_{h,QWPθ,HWPθ} and drop the wavelength/time label for conciseness. The exact series of performed measurements depends on the specific experiment.

A simple S₃ measurement measures I_LCP and I_RCP, recorded as

From this, we may calculate the quantities

with analogous processing steps for the linear components S₁ and S₂ for different waveplate angles and LCP/RCP replaced by the appropriate linear polarization axes (0°/90° and +45°/−45°, respectively). These are shown in Supplementary Information section 2.

Where appropriate, the transmission curve of long-pass filters used was measured and corrected for in data processing. Transmission characters of other optical components were not corrected for.