Arousal as a universal embedding for spatiotemporal brain dynamics

Datasets and preprocessing

Dataset 1: WashU

Animal preparation. All procedures described below were approved by the Washington University Animal Studies Committee in compliance with the American Association for Accreditation of Laboratory Animal Care guidelines. Mice were raised in standard cages in a double-barrier mouse facility with a 12–12-h light–dark cycle and ad libitum access to food and water (22 °C ambient temperature and 40–60% humidity). Experiments used n = 7 12-week-old mice hemizygous for Thy1-jRGECO1a (JAX 030525) on a C57BL/6J background, enabling optical imaging of the jRGECO1a fluorescent calcium sensor protein primarily expressed in excitatory neurons of cortical layers 2/3 and 5 (ref. ⁷³). Before imaging, a cranial window was secured to the intact skull of each mouse with dental cement under isoflurane anaesthesia according to previously published protocols⁷².

Data acquisition. Widefield imaging was conducted on a dual fluorophore optical imaging system; details of this system have been presented elsewhere^5,74. In brief, sequential illumination was provided at 470 nm, 530 nm and 625 nm; reflected light in each channel was collected by a lens (focal length = 75 mm; NMV-75M1, Navitar), split by a 580-nm dichroic (FF580-FDi02-t3-25 × 36, Semrock) into two channels, one filtered by 500-nm long pass (FF01-500/LP-25, Semrock; blocks FAF excitation, passes FAF emission and 530-nm Hb reflectance), and the other by a 593-nm long pass (FF01-593/LP-25, Semrock; blocks jRGECO1a excitation, passes jRGECO1a emission and 625-nm Hb reflectance). The two channels were detected separately via two CMOS cameras (Zyla 5.5, Andor). Data were cropped to 1,024 × 1,024 pixels, and binned to 512 × 512 to achieve a frame rate of 100 Hz in each camera, with all contrasts imaged at 25 Hz. The light-emitting diodes (LEDs) and camera exposures were synchronized and triggered via a data acquisition card (PCI-6733, National Instruments) using MATLAB R2019a (MathWorks).

Mice were head fixed under the imaging system objective using an aluminium bracket attached to a skull-mounted Plexiglas window. Before data acquisition in the awake state, mice were acclimated to head fixation over several days.

The body of the mouse was supported by a felt pouch suspended by optical posts (Thorlabs). Resting-state imaging was performed for 10 min in each mouse. Before each imaging run, dark counts were imaged for each mouse for 1 s with all LEDs off to remove background sensor noise.

Preprocessing. Images were spatially normalized, downsampled to 128 × 128 pixels, co-registered and affine transformed to the Paxinos atlas, temporally detrended (fifth order polynomial fit) and spatially smoothed (5 × 5 pixel Gaussian filter with standard deviation of 1.3 pixels)⁷⁵. Changes in 530-nm and 625-nm reflectance were interpreted using the modified Beer–Lambert law to calculate changes in oxy-haemoglobin and deoxy-haemoglobin concentration⁵.

Image sequences of fluorescence emission detected by CMOS1 (that is, uncorrected FAF) and CMOS2 (that is, uncorrected jRGECO1a) were converted to percent change (dF/F) by dividing the time trace of each pixel by its average fluorescence over each imaging run. Absorption of excitation and emission light for each fluorophore due to haemoglobin was corrected as outlined in ref. ⁷⁶. From the face videography, we derived scalar indices of pupil size via DeepLabCut software⁷⁷ and whisker motion via the Lucas–Kanade optical flow method⁷⁸ applied to and subsequently averaged across five manually selected data points on the whiskers. The resulting pupil diameter, whisker motion and widefield time series were bandpass filtered between 0.01 < f < 0.2 Hz to distinguish the hypothesized spatiotemporal process from distinct phenomena occurring at higher frequencies (for example, slow waves)⁵⁵, and to accommodate finite scan duration for 10 min. For visualization only—namely, to view the Allen atlas boundaries in register with cortical maps—we manually aligned the Paxinos-registered data from one mouse to a 2D projection of the Allen Mouse Common Coordinate Framework (v3)⁷⁹ using four anatomical landmarks: the left, right and midline points at which the anterior cortex meets the olfactory bulbs, and an additional midline point at the base of the retrosplenial cortex^3,80. Coordinates obtained from this transformation were used to overlay the Common Coordinate Framework boundaries onto the Paxinos-registered cortical maps for all mice.

Dataset 2: Allen Brain Observatory

We additionally analysed recordings obtained from awake mice and publicly released via the Allen Brain Observatory Neuropixels Visual Coding project⁸. These recordings include eye-tracking, running speed (estimated from running wheel velocity), and high-dimensional electrophysiological recordings obtained with Neuropixels probes⁸¹. We restricted analyses to the ‘functional connectivity’ stimulus set, which included a 30-min ‘spontaneous’ session with no overt experimental stimulation. Data were accessed via the Allen Software Development Kit (https://allensdk.readthedocs.io/en/latest/). From 26 available recording sessions, we excluded four with missing or compromised eye-tracking data, one lacking local field potential (LFP) data, and five with locomotion data indicating a lack of immobile periods or appearing otherwise anomalous, thus leaving a total of n = 16 recordings for downstream analyses.

Preprocessing. From the electrophysiological data, we derived estimates of population firing rates and several quantities based on the LFP. We accessed spiking activity as already extracted by Kilosort2 (ref. ²). Spikes were binned in 1.2-s bins as previously described², and a mean firing rate was computed across all available units from neocortical regions surpassing the default quality control criteria. Neocortical LFPs were used to compute BLP within three canonical frequency bands: gamma (40−100 Hz), ‘alpha’ (3−6 Hz) and delta (0.5−4 Hz). Specifically, we downsampled and low passed the signals with a 100-Hz cutoff, computed the spectrogram (scipy.signal.spectrogram⁸²) at each channel in sliding windows of 0.5 s with 80% overlap, and averaged spectrograms across all channels falling within ‘VIS’ regions (including primary and secondary visual cortical areas). BLP was then computed by integrating the spectrogram within the frequency bands of interest and normalizing by the total power. A similar procedure was applied to LFP recordings from the hippocampal CA1 region to derive estimates of hippocampal theta (5−8 Hz) and delta (0.5−4 Hz) BLP. Hippocampal SWRs were detected on the basis of the hippocampal CA1 LFP via an automated algorithm⁸³ following previously described procedures⁸⁴. In general, extreme outlying values (generally artefact) were largely mitigated through median filters applied to all observables, whereas an additional thresholding procedure was used to interpolate over large negative transients in running speed. Finally, all time series were downsampled to a sampling rate of 20 Hz and filtered between 0.01 < f < 0.2 Hz to facilitate integration with dataset 1.

Data analysis

State-space framework

Formally, we considered the generic state-space model:

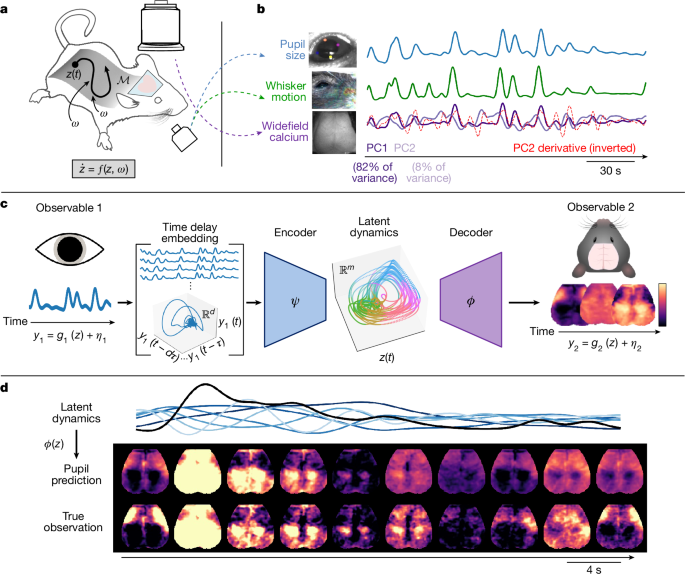
where the nonlinear function f determines the (nonautonomous) flow of the latent (that is, unobserved), vector-valued arousal state \(\bfz=[z_1,z_2,\ldots ,z_m]^\rmT\) along a low-dimensional attractor manifold \(\mathcalM\), whereas ω(t) reflects random (external or internal) perturbations decoupled from f that nonetheless influence the evolution of z (that is, ‘dynamical noise’). We consider our N observables \(\\bfy_i\_i=1^N\) as measurements of the arousal dynamics, each resulting from an observation equation g_i, along with other contributions η_i(t) that are decoupled from the dynamics of z (and in general are unique to each observable). Thus, in this framing, samples of the observable y_i at consecutive time points t and t + 1 are linked through the evolution of the latent variable z as determined by f. Note that f is presumed to embody various causal influences spanning both brain and body (and the feedback between them), whereas measurements (of either brain or body) y_i do not contribute to these dynamics. This framework provides a formal, data-driven approach to parsimoniously capture the diverse manifestations of arousal dynamics, represented by the proportion of variance in each observable y_i that can be modelled purely as a time-invariant mapping from the state-space of z.

State-space reconstruction via delays

Our principal task was to learn a mapping from arousal-related observables to the multidimensional space where the hypothesized arousal process evolves in time. To do this, we took advantage of Takens’ embedding theorem from dynamical systems theory, which has been widely used for the purpose of nonlinear state-space reconstruction from an observable. Given p snapshots of the scalar observable y in time, we began by constructing the following Hankel matrix \(\bfH\in \mathbbR^d\times (p-d+1)\):

for p time points and d time delays. Each column of H represents a short trajectory of the scalar observable y(t) over d time points, which we refer to as the delay vector h(t). These delay vectors represent the evolution of the observable within an augmented, d − dimensional state-space.

We initially constructed H as a high-dimensional (and rank-deficient) matrix to ensure it covered a sufficiently large span to embed the manifold. We subsequently reduced the dimensionality of this matrix to improve conditioning and reduce noise. Dimensionality reduction is carried out in two steps: (1), through projection onto an orthogonal set of basis vectors (below), and (2) through nonlinear dimensionality reduction via a neural network (detailed in the next section).

For the initial projection, we note that the leading left eigenvectors of H converge to Legendre polynomials in the limit of short delay windows⁸⁵. Accordingly, we used the first r = 10 discrete Legendre polynomials as the basis vectors of an orthogonal projection matrix:

(polynomials obtained from the special.legendre function in SciPy⁸²). We applied this projection to the Hankel matrix constructed from a pupil diameter timecourse. The resulting matrix \(\mathop\bfY\limits^ \sim \in \mathbbR^r\times (p-d+1)\) is given by:

Each column of this matrix, denoted \(\widetilde\bfy=\bfP^(r)\rmT\bfh\), represents the projection of a delay vector h(t) onto the leading r Legendre polynomials. The components of this state vector, \(\widetilde\bfy(t)=[y_(t),\ldots ,y_r-1(t)]^\rmT\), are the individual r Legendre coordinates⁸⁵, which form the input to the neural network encoder.

The dimensionality of H is commonly reduced through its singular value decomposition (SVD; for example, see refs. ^43,86). In practice, we found that projection onto Legendre polynomials yields marginal improvements over SVD of H, particularly in the low-data limit⁸⁵. More importantly, the Legendre polynomials additionally provided a universal, analytic basis in which to represent the dynamics; this property was exploited for comparisons across mice and datasets.

Choice of delay embedding parameters was guided on the basis of autocorrelation time and attractor reconstruction quality (that is, unfolding the attractor while maximally preserving geometry), following decomposition of H. The number of delay coordinates was guided based on asymptoting reconstruction performance using a linear regression model. For all main text analyses, the Hankel matrix was constructed with d = 100 time delays, with each row separated by Δt = 3 time steps (equivalently, adopting H as defined in equation (3), we set d = 300 and subsampled every third row). As all time series were analysed at a sampling frequency of 20 Hz, this amounts to a maximum delay window of 100 × 3 × 0.05 = 15 s.

For all modelling, pupil diameter was first shifted in time to accommodate any physiological delay between the widefield signals and the pupil. For each widefield modality, this time shift was selected as the abscissa corresponding to the peak of the cross-correlation function between the pupil and the mean widefield signal. For the leave-one-out pipeline, we used the median time shift across the six mice in the training set.

State-space mappings via VAE

To interrelate observables through this state-space framework (and thus, through arousal dynamics), we ultimately sought to approximate the target functions

where h_i(t) represents the delay vectors (columns of the Hankel matrix constructed from a scalar observable y_i), \(\bfz(t)\in \mathbbR^m\) is the low-dimensional representation of the latent arousal state, and y_j(t) is a second observable. Various linear and nonlinear methods can be used to approximate these functions (for example, see ref. ⁸⁷). Our primary results were obtained through a probabilistic modelling architecture based on the variational autoencoder (VAE)^88,89.

In brief, a VAE is a deep generative model comprising a pair of neural networks (that is, an encoder and decoder) that are jointly trained to map data observations to the mean and variance of a latent distribution (via the encoder), and to map random samples from this latent distribution back to the observation space (decoder). Thus, the VAE assumes that data observations y are taken from a distribution over some latent variable z, such that each data point is treated as a sample \(\widehatz\) from the prior distribution p_θ(z), typically initialized according to the standard diagonal Gaussian prior, that is, \(p_\theta (z)=\mathcalN(z| 0,\bfI)\). A variational distribution q_φ(z∣y) with trainable weights φ is introduced as an approximation to the true (but intractable) posterior distribution p(z∣y).

As an autoencoder, q_φ(z∣y) and p_θ(y∣z) encode observations into a stochastic latent space, and decode from this latent space back to the original observation space. The training goal is to maximize the marginal likelihood of the observables given the latent states z. This problem is made tractable by instead maximizing an evidence lower bound, such that the loss is defined in terms of the negative evidence lower bound:

where the first term corresponds to the log-likelihood of the data (reconstruction error), and the Kullback–Leibler (KL) divergence term regularizes the distribution of the latent states q_φ(z∣y) to be close to that of the prior p_θ(z). Under Gaussian assumptions, the first term is simply obtained as the mean squared error, that is, \(\parallel y-\widehaty\parallel _2^2\). The KL term is weighted according to an additional hyperparameter β, which controls the balance between these two losses^90,91. Model parameters (φ and θ) can be jointly optimized via stochastic gradient descent through the reparameterization trick⁸⁸.

In the present framework, rather than mapping back to the original observation space, we used the decoder p_θ(y∣z) to map from z to a new observation space. In this way, we used a probabilistic encoder and decoder, respectively, to approximate our target functions ψ(h) (which is partly constituted by the intermediate projection P^(r), via equation (5)) and ϕ(z). Of note, VAE training incorporates stochastic perturbations to the latent representation, thus promoting discovery of a smooth and continuous manifold. Such a representation is desirable in the present framework, such that changes within the latent space (which is based on the delay coordinates) are smoothly mapped to changes within the observation spaces⁹². After training, to generate predicted trajectories, we simply fed the mean output from the encoder (that is, q(μ_z∣y)) through the decoder to (deterministically) generate the maximum a posteriori estimate.

Model architecture and hyperparameters

VAE models were trained with the Adam optimizer⁹³ (see Supplementary Table 1 for details specific to each dataset). Across datasets, the encoder comprised a single-layer feedforward neural network with \(\tanh \) activations, which transformed the vector of leading Legendre coordinates \(\widetilde\bfy\) (equation (5)) to (the mean and log variance of) an m-dimensional latent space (m = 4 unless otherwise stated). The latent space Gaussian was initialized with a noise scale of σ = 0.1 to stabilize training. The decoder from this latent space included a single-layer feedforward neural network consisting of 10 hidden units with \(\tanh \) activations, followed by a linear readout layer matching the dimensionality of the target signal. During training, the KL divergence weight was gradually annealed to a factor of β over the first approximately 15% of training epochs to mitigate posterior collapse^90,94. Hyperparameters pertaining to delay embedding and the VAE were primarily selected by examining expressivity and robustness within the training set of a subset of mice. Within each modelling pipeline or dataset, hyperparameters were kept fixed across all mice and modalities to mitigate overfitting.

Model training pipeline

For all main analyses, we implemented an iterative leave-one-out strategy in which candidate models were trained using 10-min recordings concatenated across six of the seven mice, and subsequently tested on the held-out 10-min recording obtained from the seventh mouse. To make model training efficient, we used a randomized SVD approach^95,96. Thus, for each iteration, we began by pre-standardizing (to zero mean and unit variance) all datasets (‘standardization 1’) and aligning in time following delay embedding of the pupil measurements (thus removing the initial time points of the widefield data for which no delay vector of pupil values was available). Next, we lag adjusted the (delay embedded) pupil and widefield time series from each mouse according to the median lag (across the six training mice) derived from the cross-correlation function of each training mouse between their pupil time series and their mean widefield signal. Next, we concatenated the six training datasets and computed the SVD of the concatenated widefield time series (\(\bfY_\rmcat=\bfU_\rmcat\bfS_\rmcat\bfV_\,\rmcat^\rmT\)) to obtain group-level spatial components V_cat. Data were projected onto the leading ten components (that is, the first ten columns of V_cat) and standardized once more (‘standardization 2’), and training proceeded within this reduced subspace. Note that this group-level subspace excluded data from the test mouse, such that V_cat differed for each iteration of the leave-one-out pipeline.

For the held-out mouse, the pre-standardized pupil diameter (that is, having undergone ‘standardization 1’ above) was standardized once more using the training set parameters (‘standardization 2’), and used to generate a prediction within the group-level 10-dimensional subspace. This prediction was then inverse transformed and unprojected back into the high-dimensional image space using the standardization and projection parameters of the training set. All model evaluations were performed following one final inverse transformation to undo the initial pre-standardization (standardization 1), enabling evaluation in the original dF/F units. The pre-standardization parameters were not predicted from the training data; including the pre-standardization as part of the model would make model performance sensitive to the robustness of the relationship between dF/F values and raw pupil units, which is not scientifically relevant in this context. Finally, any subsequent projections used to evaluate model performance in terms of principal components (as in Fig. 2b) utilized mouse-specific SVD modes (denoted simply as V), rather than the group modes (V_cat) used during training.

In addition to the leave-one-out pipeline, we implemented a separate, within-subject pipeline in which we trained models on the first 5 min of data for each mouse and report model performance on the final 3.5 min of the 10-min session. This training pipeline involved prediction of the full-dimensional images, without the intermediate SVD used in the leave-one-out pipeline. All results pertaining to this modelling pipeline are contained in Supplementary Fig. 2.

Model evaluation

For analyses reporting ‘total variance’ explained (Figs. 2a and 3c, top), we report the R² value over the full 128 × 128 image, computed across all held-out time points. R² was computed as the coefficient of determination, evaluated over all pixels n and temporal samples t (that is, the total variance):

where y_n,t and \(\widehaty_n,t\) are, respectively, the true and predicted values of y at the n-th pixel and t-th time point, and \(\bary\) is the global mean. In practice, this value was computed as the pixel-wise weighted average of R² scores, with weights determined by pixel variance (computed using the built-in function sklearn.metrics.r2_score, with ‘multioutput’ set to ‘variance weighted’).

To examine variance explained beyond the first principal component (Figs. 2b and 3c, bottom), we computed the (randomized) SVD of the widefield data for each mouse (Y = USV^T) and, after training, projected the original and reconstructed widefield data onto the top N = 200 spatial components excluding the first (that is, YV_2:N) before computing R² values. The matrices from this SVD were used for all analyses involving projection onto the leading principal components.

For the shuffled control analysis (Extended Data Fig. 7), we examined total variance explained in widefield data from the test set (as in Fig. 2a), except that for each mouse, we swapped the original pupil diameter timecourse with one from each of the other six mice (that is, we shuffled pupil diameter and widefield calcium data series across mice).

Dynamic mode decomposition

Dynamic mode decomposition (DMD)^97,98,99 is a data-driven method to dimensionally reduce time series measurements into a superposition of spatiotemporal modes. Given the time series matrix Y = y(t₁), y(t₂), …, y(t_p), where y(t_i) represents the system state vector at the i-th time point, the data are split into two matrices, Y⁽¹⁾ = y(t₁), …, y(t_p−1) and Y⁽²⁾ = y(t₂), …, y(t_p). DMD seeks an approximate linear mapping A such that

Theoretically, the operator A represents a low-rank approximation to an infinite-dimensional linear operator—namely, the Koopman operator—associated with nonlinear systems^42,99, motivating the use of DMD even in the context of nonlinear dynamics. This low-rank approximation is obtained via SVD of Y⁽¹⁾ and Y⁽²⁾. The measurement data can thus be approximated in terms of the spectral decomposition of A:

where the eigenvectors v_k give the dominant spatial modes, the eigenvalues ω_k give the dominant temporal frequencies and the coefficients b_k determine the amplitudes.

For each mouse, we applied DMD separately to three data matrices: the original widefield calcium images, and the predictions generated through both the no embedding model and the latent model. Here again, for numerical efficiency, we incorporated randomized SVD as part of the randomized DMD algorithm¹⁰⁰ implemented in pyDMD^101,102.

Following application of DMD, we constructed spatial phase maps from the leading eigenvector of each A matrix. Specifically, given the leading eigenvector \(\bfv_1=[v_1,v_2,\ldots ,v_n]^\rmT\in \mathbbC^n\), we computed the phase at each pixel i as \(\theta _i=\arg (v_i)\), where \(\arg (\,\cdot \,)\) denotes the complex argument of each entry, and v_i represents the value of the eigenvector v₁ at the i-th pixel. Note that the no embedding model predictions yielded exclusively real-valued eigenvectors, as these model predictions were fundamentally rank-one (that is, they reflect linear transformations of the scalar pupil diameter). Accordingly, as the complex argument maps negative real numbers to 0 and positive real numbers to π, phase maps obtained from the no embedding model predictions were restricted to these two values.

We used the circular correlation coefficient to quantify the similarity between the phase map obtained from the original dataset and the phase map obtained from either of the two model predictions. Specifically, let θ_i and \(\widehat\theta _i\) represent the phase at spatial location i in the phase maps of the original and reconstructed datasets. The circular correlation ρ_circ between the two phase maps was computed as¹⁰³:

where \(\bar\theta \) and \(\bar\widehat\theta \) are the mean phase angles (that is, the mean directions) of the respective maps. The circular correlation is bounded between −1 and 1, where 1 indicates perfect spatial phase alignment between the datasets, and −1 indicates an inverted pattern. However, because the eigenvectors are only determined up to a complex sign, Fig. 2c reports the absolute value this quantity, that is, ∣ρ_circ∣.

Clustering and decoding analysis

We used GMMs to assign each (variance-normalized) image frame to one of k clusters (parameterized by the mean and covariance of a corresponding multivariate Gaussian) in an unsupervised manner. This procedure enables assessment of the spatial specificity of cortical patterns predicted by arousal dynamics, with increasing number of clusters reflecting increased spatial specificity.

In brief, a GMM models the observed distribution of feature values x as coming from some combination of k Gaussian distributions:

where μ_i and Σ_i are the mean and covariance matrix of the i-th Gaussian, respectively, and π_i is the probability of x belonging to the i-th Gaussian (that is, the Gaussian weight). We fit the mean, covariance and weight parameters through the standard expectation-maximization algorithm as implemented in the GMM package available in scikit-learn¹⁰⁴. This procedure results in a posterior probability for each data point’s membership to each of the k Gaussians (also referred to as the ‘responsibility’ of Gaussian i for the data point); (hard) clustering can then be performed by simply assigning each data point to the Gaussian cluster with maximal responsibility.

Images were spatially normalized such that the (brain-masked) image at each time point was set to unit variance (thus yielding a ‘spatial sign’¹⁰⁵), followed by projection onto the top three principal components to regularize the feature space. Then, for each mouse and each number of clusters k, a GMM with full covariance prior was fit to the normalized, dimensionally reduced image frames to obtain a set of ‘ground-truth’ cluster assignments. After training, this GMM was subsequently applied to the reconstructed rather than the original image frames to obtain maximum a posteriori cluster assignments associated with the no embedding or latent model predictions. These cluster assignments were compared with the ground-truth assignments, with accuracy computed as the proportion of correctly identified cluster labels.

The preceding algorithm effectively clusters the dimensionally reduced image frames on the basis of their cosine distance (technically, their L₂-normalized Euclidean distance). Because the first principal component tends to explain the vast majority of the variance, this Euclidean-based distance is largely determined by distance along the leading dimension. This analysis choice suffices for the primary purpose of the analysis—namely, to assess correspondence between the original and reconstructed data at the level of individual time points. However, in the context of multivariate data, it is common to also normalize the data features before clustering, thus equally weighting each (spatial) dimension of the data. To examine this clustering alternative, we performed feature-wise normalization of each spatial dimension following projection of the (sample-wise) normalized image frames onto the top three principal components. This essentially constitutes a whitening transformation of the image frames, with Euclidean distance in this transformed space effectively approximating the Mahalanobis distance between image frames. Clustering results from this procedure are shown in Extended Data Fig. 9. For these supplementary analyses, which we also extend to higher cluster numbers, we used a spherical (rather than full) covariance prior as additional regularization.

Hidden Markov model

We additionally used hidden Markov models (HMMs) to capture the temporal dynamics within the original and reconstructed widefield calcium measurements. In brief, under a Gaussian HMM, the observations y(t₁), y(t₂), …, y(t_p) are assumed to be generated by a sequence of latent discrete states z_t ∈ 1, …, K, with the full generative model including:

1. (1)

   A transition matrix \(\bfA\in \mathbbR^K\times K\), where A_ij = P(z_t + 1 = j∣z_t = i) represents the probability of transitioning from state i to state j.

2. (2)

   An initial state distribution, represented as a vector of state probabilities \(\boldsymbol\pi \in \mathbbR^K\) (with π_i = P(z₁ = i)).

3. (3)

   Emission distributions, such that each observation y_t is modelled as a multivariate Gaussian conditioned on the latent state z_t—that is, \(\bfy_t \sim \mathcalN(\boldsymbol\mu _z,\boldsymbol\Sigma _z)\), where μ_z and Σ_z denote the state-specific mean and covariance, respectively.

The model is thus parameterized by \(\boldsymbol\theta =\{\bfA,\boldsymbol\pi ,\\boldsymbol\mu _z,\boldsymbol\Sigma _z\_z=1^K\}\). We estimated these parameters via an expectation-maximization algorithm (Baum-Welch), as implemented in hmmlearn¹⁰⁶.

Before HMM fitting, the widefield images were projected onto the three leading principal components and normalized along each dimension (similar to preprocessing for the GMM with whitening above, but without the initial normalization of each individual image frame). HMMs were fit to these data for a range of state numbers (K = 2, 3, 4, 5, 6).

To ensure a robust fit, we initialized the state probabilities to be uniform, \(\rm\pi _i=\frac1K\), and initialized the transition matrix with probabilities of 0.8 along the diagonal (that is, within-state transitions or ‘stay’ probabilities) and 0.2/K for all off-diagonal elements (that is, between-state transitions).

An HMM was first fit to the original data (yielding a ground-truth model), and then separate HMMs were fit to the reconstructions. In the latter cases, the emission parameters \(\\boldsymbol\mu _z,\boldsymbol\Sigma _z\_z=1^K\) were fixed to the values obtained from the ground-truth model, so that only the transition matrix A and the initial state probabilities π were updated.

For each mouse and each choice of K states, we computed three evaluation metrics:

1. (1)

   The log-likelihood of the observed data under the fitted HMMs.

2. (2)

   Decoding accuracy, computed as the agreement between the latent states inferred from the ground-truth HMM and those predicted by the HMMs fit to the reconstructed datasets.

3. (3)

   Transition matrix similarity, which we computed as the row-wise KL divergence between the ground-truth and the reconstructed transition matrices:

   $$\mathbbKL(\bfA_\rmtrue\parallel \bfA_\rmmodel)=\frac1K\mathop\sum \limits_i=1^K\mathop\sum \limits_j=1^KA_ij^\rmtrue\log \fracA_ij^\rmtrueA_ij^\rmmodel.$$

   (14)

   For numerical stability in computing KL divergence, transition probabilities below a threshold of ϵ = 10⁻⁶ were set to zero and each row was renormalized to maintain stochasticity, that is,

   $$\mathop\sum \limits_j=1^KA_ij=1\quad \,\rmfor\; all\,i.$$

   (15)

Multi-dataset integration

To extend our framework to an independent set of observables, we trained our architecture on concatenated time series from the Allen Institute Brain Observatory dataset (n = 16 mice). For visualization purposes, we sought to learn a group-level two-dimensional embedding (that is, \(\bfz\in \mathbbR^2\)) based on delay embedded pupil measurements. After group-level training, we froze the weights of the encoder and retrained the decoders independently for each mouse, enabling individual-specific predictions for the Allen Institute mice from a common (that is, group-level) latent space. We additionally applied these encoder weights to delay embedded pupil observations from the original ‘WashU’ dataset, once again retraining mouse-specific decoders to reconstruct observables from the common latent space.

Once trained, this procedure results in the generative model p(y_i, z), which we used to express the posterior probability of each observable y_i as a function of position within a common 2D latent space (note that this formulation does not seek a complete generative model capturing all joint probabilities among the observables). This allowed us to systematically evaluate the conditional expectation (\(\mathbbE(\bfy_i| \bfz)\)) for each observable over a grid of points in the latent space, which was regularized to be continuous (roughly, an isotropic Gaussian⁸⁹). Figure 4 represents this expectation, averaged over decoder models trained for each mouse.

To visualize a vector field over the manifold, we applied a data-driven nonlinear equation discovery method—sparse identification of nonlinear dynamics (SINDy)^61,107—to the dynamics represented in the 2D latent coordinates, treating data from each mouse as an independent trajectory. We obtained a simple nonlinear oscillator:

with α = 0.384, β = −0.251 and γ = −0.193. This system was evaluated over a grid of evenly spaced sample points within the latent space, enabling a visual approximation of the true underlying vector field.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.