Analogue speech recognition based on physical computing

RNPU fabrication and room-temperature operation

A lightly n-doped silicon wafer (resistivity ρ ≈ 5 Ω cm) is cleaned and heated for 4 h in a furnace at 1,100 °C for dry oxidation, producing a 280-nm thick SiO₂ layer. Photolithography and chemical etching are used to selectively remove the silicon oxide. A second, 35 nm SiO₂ layer is needed for the desired dopant concentration. Ion implantation of B⁺ ions is performed at 9 keV with a dose of 3.5 × 10¹⁴ cm⁻². After implantation, rapid thermal annealing (1,050 °C for 7 s) is carried out to activate the dopants. The second oxide layer is removed by buffered hydrofluoric acid (1:7; 45 s) and then the wafer is diced into 1 cm × 1 cm pieces. E-beam lithography and e-beam evaporation are used, respectively, for creating the (1.5 nm Ti/25 nm Pd) electrodes. Finally, reactive-ion etching (CHF₃ and O₂, (25:5)) is used to etch (30–40 nm) the silicon until the desired dopant concentration is obtained.

We have consistently realized room-temperature functionality for both B-doped and As-doped RNPUs using a fabrication process that is slightly different from the previous work³. The main difference is that we do not hydrofluoric acid-etch the top layer of the RNPU after reactive-ion etching, which we expect to lead to an increased role of P_b centres⁵⁴. The observed activation energy of roughly 0.4 eV for both B-doped and As-doped devices agrees with their position in the Si bandgap and their ambipolar electronic activity. Depending on the relative concentration of intentional and unintentional dopants, and the voltages applied, we argue that both trap-assisted transport and trap-limited space-charge-limited-current⁵⁵ transport mechanisms can play a role and contribute to the observed nonlinearity at room temperature. A detailed study of the charge transport mechanisms involved will be presented elsewhere.

RNPU measurement circuitry

We use a National Instruments C-series voltage output module (NI-9264) to apply input and control voltages to the RNPU. The NI-9264 is a 16-bit digital-to-analogue converter with a slew rate of 4 V μs⁻¹ and a settling time of 15 μs for a 100-pF capacitive load and 1 V step. As shown in Fig. 2a, a small parasitic capacitance (roughly 10–100 pF) to ground is present at the RNPU output. In contrast to the previous study³, we do not measure the RNPU output current but the output voltage, without amplification. In refs. ^3,4,31, the device output was virtually grounded by the operational amplifier used for current-to-voltage conversion (Extended Data Fig. 1). Thus, the external capacitance was essentially short-circuited to ground, and no time dynamics was observed. In the present study, we directly measure and digitize the RNPU output voltage with the National Instruments C-series voltage input module (NI-9223; input impedance greater than 1 GΩ). A large input impedance, that is, more than ten times the RNPU resistance, is necessary to ensure that the time dynamics of the RNPU circuit is measurable.

Recurrent fading memory in RNPU circuit

In an RNPU, the potential landscape of the active region, which is dependent on the potential of the surrounding electrodes, determines the output voltage. In the static measurement model, the output electrode is virtually grounded. In the dynamic measurement mode (this work), however, the output electrode has a finite potential that we read with the ADC. This potential is the charge stored on the capacitor divided by the capacitance \(\left({V}_{{\rm{out}}}=\frac{Q}{{C}_{{\rm{ext}}}}\right)\). The charge on the capacitor, and hence V_out, depends on the previous inputs. The short-term (fading) memory of the circuit is therefore recurrent in nature, that is, previous inputs influence the present physical characteristics of the circuit over a typical timescale given by the time constant. More specifically, as shown in Fig. 3, an RNPU circuit is a stateful system in which the current behaviour is influenced by past events within a range of tens of milliseconds.

Extended Data Fig. 2a shows an input pulse series with a magnitude of 1 V (orange) and the output measured from the RNPU (blue). Extended Data Fig. 2b,c zoom in on the RNPU response. For each panel, we fit an exponential to extract the time constant. The time constant changes over time for the same repetitive input stimulus. We explain this by the output capacitor holding some charge from previous input pulses when the next input pulse arrives. On its turn, the potential landscape of the device is affected by the stored charge, resulting in different intrinsic RNPU impedance values.

Extended Data Fig. 3 emphasizes the nonlinearity of the RNPU response, which affects the (dis)charging rate of the RNPU circuit. A series of step functions are fed to the device (orange), and the output is measured and normalized to 1 V for better visualization (blue). Each step function has a 200 mV larger magnitude compared with the previous one. The charge stored on the capacitance, read as ADC voltage, is different for each step function, indicating that the RNPU responds to the input nonlinearly, and thus, the time constant for each input step is different. In summary, these two experiments show that the RNPU behaviour is nonlinear, dependent on both the input at t = t₀ and on preceding inputs.

TI-46-Word spoken digit dataset

The audio fragments of spoken digits are obtained from the TI-46-Word dataset¹, available at https://catalogue.ldc.upenn.edu/LDC93S9. To reduce the measurement time, we use the female subset, which contains a total of 2,075 clean utterances from 8 female speakers, covering the digits 0 to 9. The audio samples have been amplified to an amplitude range of −0.75 V to 0.75 V to match the RNPU input range and trimmed to minimize the silent parts by removing data points smaller than 50 mV (again for reducing measurement time). We used stratified randomized split to divide the dataset into train (90%) and test (10%) subsets.

GSC dataset

The GSC² dataset (available at https://www.tensorflow.org/datasets/catalog/speech_commands), is an open-source dataset containing 65,000 1-s audio recordings spoken by more than 1,800 speakers. Although the dataset comprises thousands of audio recordings, to reduce our measurement time, we selected a subset of 6,000 recordings (100 min of audio, total 64 × 100 ≈ 106 h of measurement), comprising 200 recordings per class (total 30 classes). Then, we used 11 classes as keywords and the rest as unknown (shown in Fig. 4f). No preprocessing, such as trimming silence or normalizing data, was applied to this subset before RNPU measurements. The dataset was divided into training (90%) and testing (10%) sets to assess the performance of our system. It is worth mentioning that the GSC dataset is commonly used to evaluate KWS systems that are tuned for high precision, that is, low false-positive rates. The analysis of our HWA trained model reveals that in addition to the high classification accuracy of roughly 90% (shown in Fig. 3e), the weighted F1-score for false-positive detections is roughly 91.3%.

RNPU optimization

The RNPU control electrodes are used to tune the functionality for both the linear and nonlinear operation regimes. Applying control voltages greater than or roughly equal to 500 mV pushes the RNPU into its linear regime. Furthermore, higher control voltages make the device more conductive, leading to a faster discharge of the external capacitor and, thus, a smaller time constant. In this work, we randomly choose control voltages between −0.4 V and 0.4 V except for the end-to-end training of neural networks with RNPUs in the loop (Extended Data Fig. 4). For electrodes directly next to the output, we reduce this range by a factor of two because these control voltages have a stronger influence on the output voltage.

Software-based feedforward-neural network training and inference

To evaluate the RNPU performance in reducing the classification complexity, we combined the RNPU preprocessing with two shallow ANNs: (1) a one-layer feedforward, and (2) a one-layer CNN. We trained these two models for the TI-46-Word spoken digits dataset with both the original (raw) dataset and the 32-channel RNPU-preprocessed data. For all evaluations, we used the AdamW optimizer⁵⁶ with a learning rate of 10⁻³ and a weight decay of 10⁻⁵ and trained the network for 200 epochs.

• Linear layer with the original dataset. Each digit (0 to 9) in the dataset consists of an audio signal of 1 s length sampled at a 12.5 kS s⁻¹ rate. Thus, 12,500 samples have to be mapped into 1 of 10 classes. The linear layer, therefore, has 12,500 × 10 = 125,000 learnable parameters followed by 10 log-sigmoid functions.

• Linear layer with the RNPU-preprocessed data. A 10-channel RNPU preprocessing layer with a downsampling rate of 10× converts an audio signal with a shape of 12,500 × 1 into 1,250 × 10. Then, the linear layer with 1,250 × 10 × 10 = 125,000 learnable parameters is trained. This model gives roughly 57% accuracy, which is 2% less than the 32-channel result reported in Fig. 3.

• CNN with the original dataset. The CNN model contains a 1D convolution layer with one input channel and 32 output channels, kernel size of 8, with a stride of 1, followed by a linear layer and log-sigmoid activation functions mapping the output of the convolution layer into 10 classes. The 1-layer CNN with 32 input and output channels has roughly 4,500 learnable parameters.

• CNNs with the RNPU-processed data. The CNN models used with RNPU-preprocessed data contain 1 (or 2) convolution layers with 16, 32 and 64 input channels and 32 output channels followed by a linear layer. Similar to the previous model, we used a kernel size of eight with a stride of one for each convolution kernel. The 1-layer CNN with 16, 32 and 64 channels has roughly 4,500, 8,600 and 16,900 learnable parameters, respectively.

Comparison with filterbanks and reservoir computing

Low-pass and band-pass filterbanks

The RNPU circuit of Fig. 2a would behave like an ordinary low-pass filter if the RNPU is assumed to be an adjustable linear resistor. If so, RNPUs with different control voltages could be used to realize filters with different cut-off frequencies, thus forming a low-pass filterbank. However, as argued above, the RNPU cannot be considered merely a simple linear resistive element.

Figure 2b shows the time constant of the voltage output of the circuit when the input stimulus is a voltage step of 1 V. When converting the time constants into frequency assuming a linear response, the cut-off frequency of corresponding low-pass filters can be calculated as \({f}_{{\rm{cut}}-{\rm{off}}}=\frac{1}{2{\rm{\pi }}RC}\), where R and C are the values of the device resistance and the capacitance, respectively. Given the range of the time constants in Fig. 2b, the highest and lowest cut-off frequencies of such filters are

which are below the lowest frequency the human ear can detect (20 Hz). We used this cut-off frequency range to evaluate the classification accuracy when using a linear low-pass filterbank as feature extractor (Extended Data Table 1). However, the simulation results give roughly 75% classification accuracy. This indicates that the RNPU circuit does not simply construct a linear low-pass filter with the control voltages only changing the cut-off frequency, but rather a nonlinear filterbank that mimics biological cochlea by generating distortion products.

Nonlinear low-pass filterbanks

To study the effects of nonlinear filtering on the feature extraction step, and consecutively, on the classifier performance, we have introduced biologically inspired distortion products to the output of a linear filter, more specifically, distortion products of progressively higher frequency and lower magnitude. These properties are similar to the nonlinear properties of the RNPUs. Note that we only intend to qualitatively describe the effect of distortion products on the classification accuracy here, and not to quantitatively represent the RNPU circuit.

The nonlinear filterbanks are constructed by adding nonlinear components to the output of a linear time-invariant (LTI) filter. These nonlinear components include (1) harmonic or subharmonic addition and (2) delayed input. In the frequency domain, we progressively decrease the magnitude of the nonlinear components as their frequency increase (Extended Data Table 3).

1. (1)

   Harmonic or subharmonic: given the input audio signal of x_in(t), first, we calculate the Fourier transform of the output of the LTI low-pass filter F(LPF(x_in(t))). Then, for a specific range of frequencies, for example, from the first to the hundredth frequency bin ([f₀, f₁₀₀]), we add that frequency component to the frequency harmonic at the harmonic or subharmonic position (2 × f₀, 3 × f₀, …) divided by the order of the harmonic (1/n for n × f₀). The pseudo-code of this approach is shown in Extended Data Table 3.

2. (2)

   Delayed inputs: the second nonlinear property of this nonlinear filtering is to add the delayed output of each filter (with 30% of the magnitude) to the next filter channel for a channel greater than one. Although this nonlinear inter-channel crosstalk does not occur in the RNPU circuit, our experiments have shown that this nonlinearity can help improve the classification accuracy. The time delayed has been chosen to be 10 samples, given the 1,250 S s⁻¹ sampling rate (which is the rate after downsampling the filtered signal).

To evaluate the capability of linear and nonlinear low-pass filterbanks in acoustic feature extraction, we used a similar pipeline for RNPU-processed data, that is, a 1-layer CNN with a kernel size of 3, a tanh activation function trained for 500 epochs with the AdamW⁵⁷ optimizer and a learning rate and weight decay of 0.001. We have also used the OneCycleLR scheduler⁵⁸ with a maximum learning rate of 0.1 and a cosine annealing strategy. The classifier model has been intentionally kept simple to limit its feature-extraction capabilities so that we can better evaluate different preprocessing methods.

We examined linear low-pass filterbanks under two scenarios: (1) setting the cut-off frequencies according to the RNPU circuit time constants, that is, 4 Hz and 13 Hz, for lower and higher limits, respectively, and (2) setting a wider range of cut-off frequencies, that is, 20 and 625 for the lower and higher limits, respectively. The higher limit for the latter case is based on the Nyquist frequency given the 1,250 S s⁻¹ sampling rate. The inference accuracy results for the same TI-46-Word benchmark test are summarized in Extended Data Table 1.

Nonlinear band-pass filterbanks

The hair cells of the basilar membrane in the cochlea convert acoustic vibrations into electrical signals nonlinearly, in which small displacements cause a notable change in the output at first. However, as the displacements increase, this rate slows down and eventually approaches a limit. It has been proposed that this with nonlinearity (CN) can be modelled as a hyperbolic tangent (tanh) function. Similar to nonlinear low-pass filterbanks, we implemented a nonlinear band-pass filterbank as a model for auditory filters in the mammalian auditory system. The model is constructed by an LTI filterbank of band-pass filters (fb_band-pass) initialized with gammatone within 20 Hz to 625 Hz followed by the tanh nonlinearity described as follows:

where X represents the input audio signal. For simulations with this nonlinear band-pass filterbank, we use the same classifier model (1-layer CNN) with the same hyperparameters described before. The performance of this nonlinear filterbank is summarized in Extended Data Table 1. Adding the tanh nonlinearity increases the overall classification accuracy to more than 93%, which is notably higher than the LTI band-pass filterbank but still less than the value obtained with RNPU preprocessing.

Reservoir computing

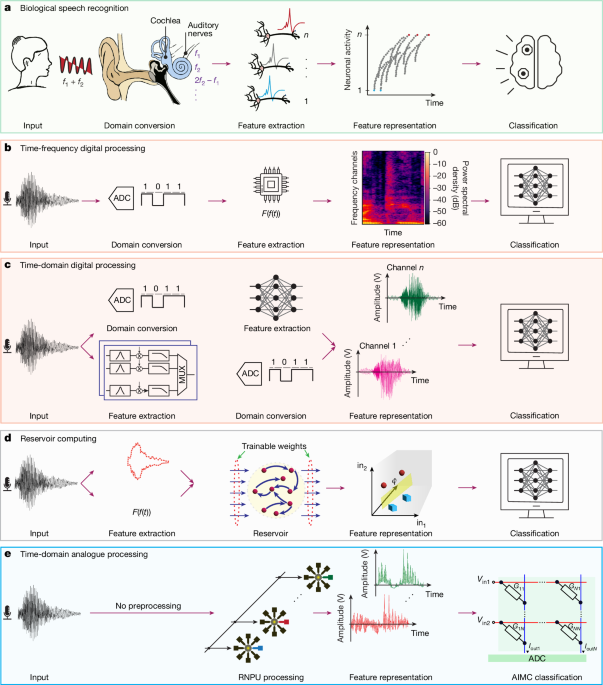
Here we make a comparison with reservoir computing, in particular with echo state networks (ESNs). ESNs are reservoir computing-based frameworks for time-series processing, which are essentially randomly initialized recurrent neural networks⁵⁹. ESNs offer nonlinearity and short-term memory essential for projecting input data into a high-dimensional feature space, in which the classification of those features becomes simpler. As reported in the main text, most reservoir computing solutions for speech recognition rely on frequency-domain feature extraction. More specifically, a reservoir is normally used to project pre-extracted features into a higher-dimensional space and then a classifier, often a linear layer, is used to perform the classification.

Here, we compare the efficacy of ESNs for acoustic feature extraction to RNPUs and filterbanks. Using the ReservoirPy Python package⁶⁰, we modelled 64 different reservoirs initialized with random conditions for neuron leak rate (lr), spectral radius of recurrent weight matrix (sr), recurrent weight matrix connectivity (rc_connectivity) and reservoir activation noise (rc_noise). Then, the same dataset as described in the main text is fed to all these reservoir models, and the output is used for classification. The reservoir maps the input to output with a downsampling rate of ten times, the same as for RNPUs and filterbanks. The performance of using reservoirs as feature extractors is summarized in Extended Data Table 1. Notably, this approach performs the poorest among other feature extractors. We attribute this low classification rate to the absence of bio-plausible mechanisms for acoustic feature extraction in the reservoir system. More specifically, although a reservoir projects the input into a higher-dimensional space, the lack of compressive linearity, a recurrent form of feedback from the output, and frequency selectivity make acoustic feature extraction with reservoirs less effective compared with other solutions.

AIMC CNN model development

We implemented two CNN models for classification of the TI-64-Word spoken digits dataset on the AIMC chip with 2-layer and 3-layer convolutional layers, trained with 32 and 64 channels of RNPU measurement data, respectively. Extended Data Fig. 3 illustrates the architecture of the 3-layer convolution layer with 64 RNPU channels (roughly 65,000 learnable parameters). The first AIMC convolution layer receives the data from the RNPU with dimensions of 64 × 1,250. To implement this layer with a kernel size of 8, 64 × 8 = 512 crossbar rows are required. To optimize crossbar array resource use, this layer has 96 output channels. Thus, in total, 512 rows and 96 columns of the AIMC chip are used (Fig. 4c) to implement this layer. The second and third convolution layers both have a kernel size of three. Considering the 96 output channels, each layer requires 96 × 3 = 288 crossbar rows (Fig. 4c). Finally, the fully connected layer is a 36 × 10 feedforward layer.

AIMC training and inference

The AIMC training, done in software, consists of two phases: a full-precision phase and a retraining phase, each performed for 200 epochs. The retraining phase is performed to make the classifier robust to weight noise arising from the non-ideality of the PCM devices and the 8-bit input-quantization. During this second phase, we implement two steps: (1) in every forward pass, random Gaussian noise with a magnitude equalling 12% of the maximum weight is added to each layer of the network, as well as Gaussian noise with a standard deviation of 0.1 is added to the output of every MVM to make the model more robust to noise, and (2) after each training batch, weights and biases are clipped to 1.5 × σ_W implementing the low-bit quantization, where σ_W is the standard deviation of the distribution of weights.

RNPU static power measurement

To estimate the RNPU energy efficiency, we measured the static power consumption, P_static, for ten different sets of random control voltages and averaged the results. In every configuration, a constant d.c. voltage is applied to each electrode, and the resulting current through every electrode is measured sequentially using a Keithley 236 source measure unit. P_static is calculated according to

where N = 8 is the number of electrodes of the device.

As illustrated in Extended Data Fig. 2, the average static power consumption <P_static> of the measured RNPU is roughly 1.9 nW. For an estimate of the RNPU power efficiency, we use a conservative value of 5 nW, leading to 320 nW for 64 RNPUs in parallel, which is roughly 3 times lower than realized with analogue filterbanks reported in ref. ²⁵. However, it is worth emphasizing that the advantage of RNPU preprocessing extends beyond this improvement by simplifying the classification step, as illustrated in Fig. 2.

System-level efficiency analysis

The 6-layer CNN model for the GSC dataset, implemented on the IBM HERMES project chip, possesses roughly 470,000 learnable parameters and requires 120 M MAC operations per RNPU-preprocessed audio recording (all audio recordings have a duration of 1 s). On deployment of the AIMC chip, the model occupies 18 out of the available 64 cores (28% of the total number of cores), as depicted in Fig. 4e. Since the present chip is not designed and optimized for the studied tasks, but rather serves a general purpose, in each core some memristive devices remain unused causing the efficiency to drop.

In this regard, it is necessary to mention that we use experimental measurement reports from ref. ⁵ when the chip operates in one-phase read mode, although the reported inference accuracies are for the four-phase mode. The latter approach reduces the chip’s maximum throughput and energy efficiency by roughly four times, while accounting for circuit and device non-idealities. Our decision to report the results based on the one-phase read mode is recently supported by the literature⁵⁷, as evidenced by the experimental demonstration of a new analogue or digital calibration procedure on the same IBM HERMES project chip. This procedure has been shown to achieve comparable high-precision computations in the one-phase read mode as those achieved in the four-phase model.

Convolution layers 0 to 3 in Fig. 4d of the main text require 1977, 492, 121 and 28 MVMs per number of occupied cores, respectively. Therefore, the total number of MVMs (including two fully connected layers) is \(\mathop{\sum }\limits_{l=0}^{5}{{\rm{MVMs}}}_{l}\times {\rm{num}}\_{\rm{cores}}={\rm{5,861}}\). The IBM HERMES project chip consumes 0.86 µJ at full use (for all 64 cores) for MVM operations with a delay of 133 ns. Consequently, the classifier model consumes \(\frac{5,\,861}{64}\times 0.86\,{\rm{\mu }}{\rm{J}}=78.7\,{\rm{\mu }}{\rm{J}}\). Similarly, the end-to-end latency can be calculated as \(\mathop{\sum }\limits_{l=0}^{5}{{\rm{MVMs}}}_{l}\times 133\,{\rm{ns}}=2,\,619{\rm{\times }}133\,{\rm{ns}}=348.3\,{\rm{\mu }}{\rm{s}}\). Note that a layer (weight) matrix is typically partitioned into submatrices to be fitted on the AIMC crossbar core⁵⁷. In our calculations, we assume that these submatrices are mapped to different cores and, therefore, the partial block-wise MVMs are executed in parallel.

Our evaluation approach stands on the conservative side for MVM energy consumption; for instance, we assume energy consumption of one core for linear layers with 17,152 learnable parameters (out of 262,144 memristive devices of a core, which is only 6.5% use). However, we assume negligible energy consumption due to (local) digital processing, which rounds for roughly 7% of the total energy consumption (28% core use × 27% local digital processing unit’s part out of total static power consumption). Further, because of batch-norm and maximum-pooling layers, we buffered MVM results of each layer on memory, which introduces extra delay to the computations. However, for real-world tasks, we can avoid CNNs but rather use large multilayer perceptrons or recurrent neural networks instead.

Comparing energy consumption and latency with state of the art

We conducted a comparative analysis of the system-level energy consumption and latency of our architecture with other state-of-the-art speech-recognition systems, summarized in Extended Data Table 2. Dedicated digital speech-recognition chips consume the lowest amount of energy per inference. Nevertheless, because of the long latency of computations, their energy-delay product) is markedly high. A recent KWS task implemented on an AIMC-based chip has shown classification latency reduction, specifically, 2.4 μs compared with a 16-ms delay of digital solutions. However, this approach is based on extensive preprocessing that includes extracting mel-frequency cepstral coefficient features and pruning the features to increase the classification accuracy. Furthermore, not reporting the energy consumption, and only considering the classification latency (excluding preprocessing) are the reasons that make a direct comparison impossible.

It is worth mentioning that our energy estimate for the AIMC classification stage is based on experimental measurements from a prototype AIMC tile⁵. Similar to any emerging technology, we anticipate that these energy figures will notably improve as the technology matures beyond the prototyping stage³⁹. These improvements are expected to occur at not only the peripheral circuitries, but also at the PCM device level: active efforts are already underway in both areas.

In AIMC, integration time and the ADC power consumption are major sources of the total energy consumption. In the AIMC chip used in this work, clock transients and the bit-parallel vector encoding scheme limit the MVM latency to roughly 133 ns. However, bit-serial encoding scheme and increasing the clock frequency is now being explored to reduce the integration time below around 50 ns. Furthermore, ADCs at the moment account for up to 50% of the total power consumption⁵. Efforts are underway to adopt time-interleaved, voltage-based ADCs, potentially in a design that avoids power-hungry components, such as operational transimpedance amplifiers. These design improvements will substantially reduce power consumption while also further improving conversion speeds through a single ADC conversion for signed inputs. Furthermore, introducing power gating techniques, which are not implemented at present, can further reduce ADC energy usage during idle periods.

At the PCM device level optimization, research is being conducted to reduce the conductance values of the programmable non-volatile states. Recent experimental measurements have shown that a more than ten times reduction in the conductance values can be achieved⁶¹, which can lead to proportional improvements in energy efficiency at the crossbar level. Taking all these enhancements into account, a conservative future estimate places the energy per inference in the range of roughly 10 μJ, which would also make AIMC systems competitive with state-of-the-art ASR processors in terms of energy efficiency.