Analog optical computer for AI inference and combinatorial optimization

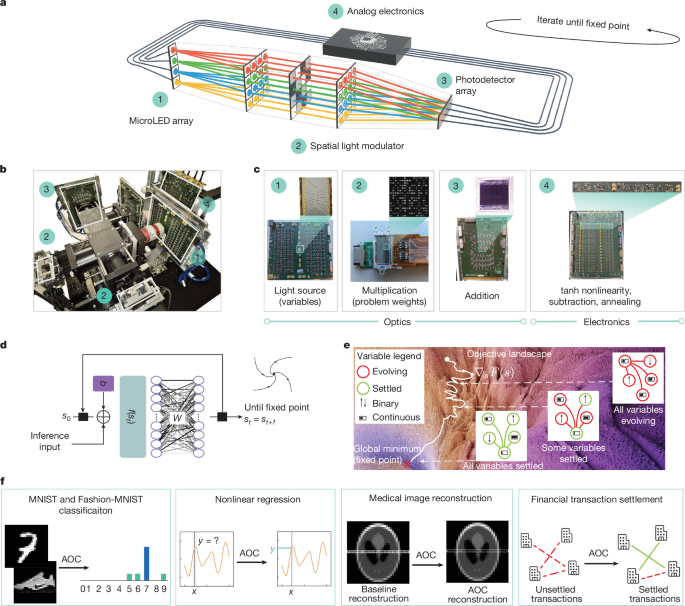
Experimental set-up

The key components of our experimental set-up are shown in Fig. 1a and Extended Data Fig. 1.

Optical subsystem

The optical subsystem performs matrix–vector multiplication. The basic components are the optical sources (input vector), a system of fan-out optics to project the light onto the modulator matrix and a system of fan-in optics to project the light onto a photodetector array (output vector). The corresponding schematic is shown in Extended Data Fig. 2.

The incoherent light sources are an array of 16 independently addressable microLEDs. Each microLED is driven with a bias current and an offset voltage. The variable value is encoded by the light intensity, with a value of zero corresponding to the microLED bias point. Mathematical positive values are represented by microLED drive currents greater than the bias value. Negative values are represented by drive currents less than the bias value. The diameter of each emitter is 50 μm and the pitch is 75 μm. The sources are fabricated in gallium nitride wafers on a sapphire substrate and the die is wire-bonded onto a printed circuit board (Fig. 1c). The emission spectrum is centred at 520 nm with a full-width of half-maximum of 35 nm and the operational −3-dB bandwidth is 200 MHz at 20 mA, see Supplementary Fig. 1.

After the sources, there is a polarizing beamsplitter (PBS). From this point, there are two equivalent optical paths in this set-up. Each path performs two functions: first, they allow us to use both polarizations of the unpolarized light output; second, they allow us to perform non-negative and non-positive multiplications with only intensity modulation. Each path contains one amplitude modulator matrix and one photodetector array. The modulator matrix is a reflective parallel-aligned nematic liquid-crystal SLM. We refer to the first part of the optical system as the fan-out system. The task of this fan-out system is to image the microLEDs onto the SLM, where the weights are displayed, and to spread the light horizontally into lines. The microLEDs are arranged in a one-dimensional line (let this be the y axis) and are imaged onto the SLM using a 4F system composed of a high-numerical-aperture (Thorlabs TL10X-2P, numerical aperture 0.5, ×10 magnification, 22-mm field number) collection objective and a lower-numerical-aperture lens group composed of 2 achromatic doublets with combined focal length 77 mm. There is a cylindrical lens, Thorlabs LJ1558L1, in infinity space of this 4F system. This lens adds defocus to the image of the source array on the SLM but only in the x direction, so that the projected light pattern is a set of long horizontal lines, one per microLED. Each matrix element occupies a patch of 12 (height) × 10 (width) pixels of the modulator array. An 8-bit look-up table is used to linearize the SLM response as a function of grey level.

The SLM is imaged onto the photodetector array using a 4F system (the fan-in system). The first lens group of the fan-in is the same as the second lens group of the fan-out system as this is in double pass. From here, the light is directed towards the intended photodetector array through a second PBS. The light from each column of the SLM is collected by an array of 16 silicon photodetectors to perform the required summation operation. The active area of each element is 3.6 × 0.075 mm². The photodetectors are on a pitch of 0.125 mm. The operation bandwidth is 490 MHz at −10 V measured at 600 nm.

Analog electronic subsystem

After the photodetector array, the signals are in the analog electronic domain. The photocurrents from each photodetector element are amplified by a linear trans-impedance amplifier (Analog Devices MAX4066). Each trans-impedance amplifier provides 25-kΩ gain and is characterized by an input referred noise of \(3\,\rmpA\,\sqrt\textHz\) and has differential outputs. The corresponding 2 sets (1 per photodetector board) of 16 differential pairs of signals are fed to the main boards where the per-channel nonlinear operation and other analog electronic processing is carried out. Each of the 16 signals sees the following circuitry: (1) a variable gain amplifier (VGA; Texas Instruments VCA824) to allow the input signal range to be set and equalized across channels; (2) a difference amplifier to perform the operation of subtracting the negative input signal from the positive one and achieve signed voltages (signed multiplications); (3) a VGA that adds and subtracts signals from the described path, referred to as gradient term, to the annealing and momentum terms, as per equation (1), while providing a common gain control to all these paths; (4) an electronic switch (ADG659) to open and close the loop to set and reset the solving state; (5) a buffer amplifier to distribute the signal to the gradient, annealing and momentum paths; (6) a bipolar differential pair to implement the tanh nonlinearity; (7) a VGA to adjust the signal level between the nonlinearity and the required voltage and current onto the microLED alternating-current input circuit. Both the annealing and momentum paths have VGAs with a common external control so that we can implement time-varying annealing and momentum schedules.

Each channel also has an offset to the common control signal added to allow minor adjustment or correction of channel-to-channel variations. The other VGAs are set with digital-to-analog converters controlled over an inter-integrated circuit (I2C) bus. This allows slower control at per-experiment timescales.

Nonlinearity

The per-channel nonlinear function is an approximation to a tanh. This is shown in Supplementary Fig. 5d. The system is designed so that all signals follow the same path through the solver. For ML workloads, the input domain of the tanh function is unrestricted by hardware; there are no gain variations across channels. The trained weights and equilibrium model input ensure that signals evolve accurately. For optimization workloads, binary and continuous variables require different handling in hardware. Here we set the gain after the trans-impedance amplifier and before the tanh nonlinearity to be lower for continuous variables than for binary variables. This adjustment ensures that the input domain of the nonlinearity results in a more linear output for continuous variables than for binary variables.

Evaluation of matrix–vector multiplication accuracy

We characterized and calibrated the key opto-electronic and electronic components to equalize the gain of each AOC path. For example, we calibrate the optical paths by applying a set of 93 reference matrices and for each we digitally compute the result of the vector–matrix product. We then adjust the gain per channel slightly so that, averaged over the set of 93 computed vectors, the AOC result is as close as possible to the digital result.

Following this, the accuracy of the matrix–vector multiplication is characterized using the same 93 reference matrices on each SLM and measuring the output of the system, shown in Supplementary Fig. 3a. For each reference matrix in the set, we calculate the MSE between the known and the measured output. The mean MSE across all dot products is 5.5 × 10⁻³, and the matrix–vector multiplication MSE as a function of matrix (instance) is shown in Supplementary Fig. 3b. For these experiments, we configure the system in open-loop mode without feedback and turn off the annealing and momentum paths.

ML methods

Training and digital twin

In commercial deployments, training consumes less than 10% of the energy and, hence, is not targeted by the AOC. The equilibrium models are trained through our digital twin, which is based on equation (2). In the digital domain during training, the convergence criterion is set to ∣∣s_t+1 − s_t∣∣ < ε, with ε = 10⁻³. The AOC-DT models up to seven non-idealities measured on the AOC device; each non-ideality can be switched on and off (Supplementary Fig. 5). The AOC-DT is implemented as a Pytorch module with the weight matrix W and bias terms b, as well as the gain β as trainable parameters. The weight matrix is normalized to fulfil ∥W∥_∞ = 1 throughout training to simulate the passive SLM. The numeric scale of the matrix is instead modelled by the gain β. This separation of scale is necessary as several nonlinear non-idealities occur between the matrix multiplication and the gain in equation (2), as discussed in Supplementary Information section D.

The weight matrix is initialized with the default Pytorch initialization for a 16 × 16 matrix, the bias term is initialized to 0 and β is initialized at 1. We trained all models with a batch size of B = 8, at a learning rate of η = 3 × 10⁻⁴ for MNIST and Fashion-MNIST and η = 7 × 10⁻⁴ for regression tasks. We used the Adam optimizer⁵⁰. In all cases, models are trained end-to-end, with the equilibrium-section trained through our AOC-DT using the implicit gradient method¹⁷, which avoids storing activations for the fixed-point iterations. This decouples memory cost from iteration depth as intermediate activations do not need to be stored. In all experiments, the α gain in equation (2) is set to 0.5 to strike a balance between overall signal amplitude and speed of convergence. Low α values cause the signal to be too weak, resulting in a low signal-to-noise ratio (Supplementary Information section D).

Inference and export to the AOC

Once training has completed, the weight matrix W is quantized to signed 9-bit integers using

with the rounded and clamped matrix on the right-hand side being the quantized weight matrix W_Q. Whenever we report AOC-DT results, we report results obtained with the quantized matrix.

Exporting trained models to the AOC requires several further steps. First, the model inputs x and the bias term b need to be condensed into a single vector b_AOC = b + x followed by clamp to ensure the values fit into the dynamic range of the AOC device (Supplementary Information section D). Second, as the optical matrix multiplication is implemented using SLMs, elements of the weight matrix are bounded by one such that all quantization-related factors disappear. However, the original maximum element of the matrix max(W) needs to be re-injected, which we achieve via the β gain in equation (2), approximately restoring the original matrix W.

The quantized matrix is split into positive and negative parts, \(W_\rmQ=W_\rmQ^+-W_\rmQ^-\), and each part is displayed on its respective SLM.

AOC sampling and workflow

Each classification instance (that is, MNIST or Fashion-MNIST test image) is run once on the AOC, and the fixed point is sampled at the point marked in Extended Data Fig. 3 after a short 2.5–μs cooldown window after the switch is closed, as shown in Extended Data Fig. 5a,b. The sampling window extends over 40 samples at 6.25 MHz, corresponding to 6.4 μs. This ensures that the search of fixed points for the equilibrium models happens entirely in the analog domain. Once sampled, we digitally project the vector into the output space. For classification, the input is projected from 784 to 16 dimensions, the output is projected from 16 to 10 classes. The label is then determined by the index of the largest element in the output vector (argument-max). For regression tasks, the IP and OP layers transform a scalar to 16 dimensions and back, respectively. The MSE results in Fig. 2c were obtained by averaging over 11 repeats for each input. This means that we restart the solution process 11 times, including the sampling window, and average the resulting latent fixed-point vectors. Importantly, the solve-to-solve variability appears to be centred close to the curve produced by the AOC-DT, enabling us to average this variability out (Supplementary Fig. 6).

The 4,096-weight ensemble model

We can expand the model sizes supported by the hardware by using an ensemble of small models that fit on it. These smaller 256-weight models are independent at inference time but are trained jointly by receiving slices 16-sized slices of a larger input vector and stacking their outputs before the OP. To scale to a 4,096-weight equilibrium model, we expand the input space from 16 to 16 × 16 = 4,096 dimensions and the output space from 10 to 10 × 16 = 160 dimensions. The IP matrix is consequently a 784 × 4,096-shaped matrix and the OP matrix is shaped 160 × 10. MNIST or Fashion-MNIST images are scaled to the range [−1, 1] and, projected to 4,096 dimensions and split into 16 slices of 16 dimensions. Each of the 16 equilibrium models then runs its respective slice of input vectors to a fixed-point. Once all 16 models are run on the AOC, we concatenate outputs and project them into the 10-dimensional output space where the largest dimension determines the predicted cipher.

Nonlinear regression

The first curve (I) is a Gaussian rescaled such that the Gaussian curve approximately stretches from −1 to 1, \(f_\rmI(x)=2\rme^-x^2/2\sigma ^2-1\) for σ = 0.25 and x ∈ [−1, 1]. The second curve (II) is given by \(f_\rmII(x)=\sqrt x\,\sin (3\rm\pi x)\). For training sets, we choose 10,000 equidistant points x_i in the range [−1, 1] whereas for test regression datasets, we choose 200 points randomly x_i ≈ U([−1, 1]).

Error estimation

For regression tasks, we concatenate the 40 samples from all 11 repeats and calculate the standard deviation per point on the curve.

Classification datasets

We trained the MNIST and Fashion-MNIST models on 48,000 images from their respective training set, validated on a set of 12,000 images and tested them on the full test set comprising 10,000 images.

Error estimation

For experimental results, the error bars in Fig. 2d were estimated using a Bayesian approach for the decision variable c_t ∈ 0, 1, …, 9 for each sample t along the sampling window per image. We assume an uninformative prior p(c_t) = beta(1, 1), which we then update with the observed number of correct decisions n_success and failures n_failure over the sampling window. The variance of the conjugate posterior of a beta distribution is given by \(\mathrmVar(c_t| n_\mathrmsuccess,n_\rmfailure)=\frac(1+n_\mathrmsuccess)(1+n_\mathrmfailure)(2+n_\mathrmsuccess+n_\mathrmfailure)^2(3+n_\mathrmsuccess+n_\mathrmfailure)\). We use this to estimate the variance and, by taking the square root, the standard deviation per input image. The dataset error bars are then estimated as the mean of the standard deviations over all members of the dataset.

Optimization methods

Positive and negative problem weights

To address optimization problems involving positive and negative weights on the AOC hardware, QUMO instances without linear terms can have up to eight variables, which applies to both transaction-settlement scenarios and reconstruction of one-dimensional line of the Shepp–Logan phantom image. The weight matrices are unsigned in synthetic QUMO and QUBO hardware benchmarks; hence the AOC hardware can accommodate up to 16-variable instances in the absence of linear terms. Such instance size difference arises because, when both positive and negative weights are present, non-idealities in the dual-SLM configuration reduce the accuracy of matrix–vector multiplication. To mitigate this, a single SLM is used to process both positive and negative weights, effectively halving the number of variables per instance.

Industrial optimization problems

For the transaction-settlement scenario and the Shepp–Logan phantom image slice, their 41-variable and 64-variable QUMO instances are decomposed into smaller 7-variable QUMO instances. For each of these subinstances, the 7 variables are connected with the rest of the variables via a linear vector b, which is incorporated into the quadratic matrix W via an additional binary variable. This decomposition is repeated for each subinstance and the linear vector b is updated at the end of each BCD iteration to create the next QUMO instance. Such an approach yields 8-variable QUMO instances and a single SLM is used to represent their positive and negative matrix elements, with analog electronics handling their subtraction, which effectively utilizes the full 16-variable capacity available in hardware. The required number of BCD iterations varies depending on factors such as the initial random state of the optimization instance variables, the selection of variable blocks among subinstances, and the order in which they are optimized.

For the one-dimensional Shepp–Logan phantom image, 12 out of 32 measurements are omitted, corresponding to a 37.5% data loss or a 1.6 undersampling (acceleration) rate. Although typical MRI acceleration ranges from 2 to 8, this rate is used here owing to the image’s non-smoothness at a 32-pixel resolution.

Binary and continuous variables

In the AOC, binary variables are encoded using a hyperbolic tangent function, whereas continuous variables utilize the near-linear region of the function, connecting optimization variables to state variables via x = f(s). In simulations at scale with the AOC-DT, linear and sign functions are used for continuous and binary variables, respectively.

Hardware QUMO instances

To ensure that some variables take indeed continuous values in the global optimal solution, we plant random continuous values and generate synthetic 16-variable QUMO instances. As the number of continuous variables increases for a given problem size, the problem instances become computationally easier to solve. Consequently, we consider instances with up to eight continuous variables.

Hardware QUBO instances

We generate up to 8-bit dense and sparse instances. The sparse instances belong to the QUBO model on three-regular graphs that are NP-hard⁵¹, although NP-hardness does not imply that every random instance is difficult to solve. To make these instances more challenging to solve, we verify that their global objective minimizer is distinct from the signs of the principal eigenvector of the weight matrix⁵².

QPLIB benchmark

The QPLIB is a library of quadratic programming instances²³ collected over almost a year-long open call from various communities, with the selected instances being challenging for state-of-the-art solvers. As described in the main part of the paper, we consider only the hardest instances within the QPLIB:QBL class of problems, which contains instances with quadratic objective and linear inequality constraints. The QPLIB:QCBO class of problems, which contains instances with quadratic objective and linear equality constraints, and the QPLIB:QBN class of problems, which contains QUBO instances, are considered in Supplementary Information section G.5.

AOC-DT operation and parameters

The distinction of the AOC-DT algorithm is the simultaneous inclusion of both momentum and annealing terms, which markedly improves the performance of the standard steepest gradient-descent method on non-convex optimization problems. Typically, multiple hyperparameters need to be calibrated for heuristic methods to achieve their best performance in solving optimization problems. We consider \(\alpha (t)=1-\widehat\alpha (t)\), where \(\widehat\alpha (t)\) is a linearly decreasing function from some initial value α₀ to 0 over time. From the hardware perspective, such an annealing schedule provides an explicit stopping criteria, which is an advantage for an all-analog hardware implementation as it avoids the complexity of multiple intermediate readouts that stochastic heuristic approaches suffer from⁵³. In principle, the three main parameters α₀, β, γ of the AOC fixed-point update rule need to be adjusted for each optimization instance. In our simulations, we notice that the algorithm is less sensitive to the momentum parameter value, whereas the α₀ and β values substantially affect the solution quality. We further perform a linear stability analysis of the algorithm to evaluate reasonable exploration regions for these two parameters and find that by scaling the β parameter as β = β₀/λ_largest, where λ_largest is the largest eigenvalue of the weight matrix W, we get scaled parameters β₀ and α₀ being in a similar optimal unit range across a wide range of problems.

We design a two-phase approach for the AOC-DT to operate similar to a black-box solver that can quickly adjust the critical parameters within the given time limit. During the ‘exploration’ phase, we evaluate the relative algorithm performance across a vast range of parameters (α₀, β₀). A subset of ‘good’ parameters is then passed for more extensive investigation in the ‘deep search’ phase (Supplementary Information section G.1).

We note that for two QPLIB:QUMO instances, namely, 5,935 and 5,962, we developed a pre-processing technique that greedily picks variables with the highest impact on the objective functions and considers their possible values, which is accounted in the reported time speed-up of the AOC-DT.

Competing solvers

For a fair comparison, we ensure that all methods use similar computing resources. Although the implementation of GPU- or central-processing-unit-based solvers can require highly varying engineering efforts, we try to estimate the cost of running solvers on the hardware, on which they are designed to run, and vary the time limit across solvers accordingly to ensure similar cost per solver run. In what follows, the Julia-based AOC-DT runs on a GV100 GPU for 5–300 s per instance across all benchmarks. In the case of Gurobi, our licence allows us to use only up to eight cores, and its time to achieve the best solution for the first time is used (not the time to prove its optimality).

More details about the AOC hardware and the AOC-DT performance on different optimization instances are provided in Supplementary Information section G.5.