Abyssal seafloor as a key driver of ocean trace-metal biogeochemical cycles

Particle scavenging

We quantitatively partitioned scavenged Nd into fractions associated with each particle type. First, we estimated the particle-specific partition coefficients of Nd. Assuming reversible scavenging, the concentration of scavenged Nd (Nd_s) is:

where i is the index of particle type, including Mn oxide, Fe oxide, POM, calcium carbonate (CaCO₃), opal and lithogenic particle, \({K}_{{\rm{d}}}^{i}\) and Cⁱ are the apparent partition coefficient and particle concentration of the ith particle type, and Nd_d is the total dissolved Nd concentration. Here we assume that \({K}_{{\rm{d}}}^{i}\) is a constant, a standard practice in the literature^24,39. When using the total dissolved concentration in equation (1), \({K}_{{\rm{d}}}^{i}\) is an apparent constant, as in principle it should depend on metal speciation⁵⁹. Given the relative uniformity of deep-ocean properties, it is reasonable to assume that speciation in seawater is roughly the same and treat \({K}_{{\rm{d}}}^{i}\) as a constant. However, in pore water, speciation can strongly differ from seawater and changes with sediment depth; it is thus preferable to model \({K}_{{\rm{d}}}^{i}\) as a variable (see below).

Equation (1) is rewritten following refs. ^24,39:

where TP is the total particle concentration, \({K}_{{\rm{d}}}^{{\rm{TP}}}\) is the total particle partition coefficient and fⁱ is the mass fraction of the ith particle type.

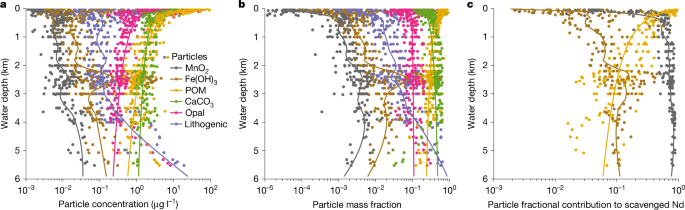
We used data from the GEOTRACES Pacific GP16 and Atlantic GA03 cruises to characterize the particle scavenging of Nd (refs. ^25,38,60,61). These are so far the only cruises reporting both dissolved and particulate Nd data, as well as necessary bulk particulate data to carry out this analysis. The particulate data were size-fractionated (small particle, about 1–51 μm; large particle, >51 μm). Here we assume that K_d is not size specific. The GEOTRACES dissolved and particle samples were collected using Niskin bottles and McLane pumps, respectively, and thus are from slightly different depths. To create a paired dataset, we interpolated the dissolved Nd concentration at the depths of the particulate data.

The concentration of scavenged Nd is calculated by removing the lithogenic background from the measured total particle Nd concentration. In the original studies^25,60, titanium (Ti) and aluminium (Al) were used for detrital correction of the Atlantic GA03 and Pacific GP16 data, respectively, to estimate the concentrations of lithogenic particle and authigenic Fe oxide and Mn oxide. To be consistent, we also used Ti and Al for detrital correction of Nd at the GA03 and GP16 sites, respectively, assuming that the detrital Nd/Ti or Nd/Al ratio is the same as the upper continental crust⁴¹.

Equation (2) forms a system of equations that we solved for \({K}_{{\rm{d}}}^{i}\) using least-square estimation. To ensure the non-negativity of \({K}_{{\rm{d}}}^{i}\), the estimation was performed in terms of \({\log }_{10}{K}_{{\rm{d}}}^{i}\). We used a global black-box optimization method with constraints (ranges of \({\log }_{10}{K}_{{\rm{d}}}^{i}\) were set to −10 to 10) from the Julia package BlackBoxOptim.jl⁶². To account for data heterogeneity and provide error estimates, we performed the estimation 1,000 times by randomly sampling 75% of the data each time. When all particle data were used, the estimation gave \({\log }_{10}{K}_{{\rm{d}}}^{i}\) values of 8.66 (median, 8.63 to 8.72 interquartile range), 7.21 (7.17 to 7.26), 5.55 (5.10 to 5.81), 6.12 (5.92 to 6.22), −2.33 (−9.53 to 5.38) and −9.53 (−9.79 to −9.24) for Mn oxide, Fe oxide, POM and CaCO₃, lithogenic particles and opal, respectively. This shows that lithogenic particles and opal are negligible scavengers of Nd, consistent with the observation that \({K}_{{\rm{d}}}^{{\rm{TP}}}\) has no statistically significant (P > 0.1) relationship with lithogenic particles and opal fⁱ. However, if we restrict the particle data to below the surface (>200 m), our estimate shows that \({\log }_{10}{K}_{{\rm{d}}}^{i}\) of Mn oxide, Fe oxide and POM still have narrowly defined distributions overlapping with the aforementioned estimates, but \({\log }_{10}{K}_{{\rm{d}}}^{i}\) of CaCO₃ has a bimodal distribution with a wide interquartile range of −8.93 to 6.07 (median of 5.74), consistent with the observation that the correlation of \({K}_{{\rm{d}}}^{{\rm{TP}}}\) with \({f}^{{{\rm{CaCO}}}_{3}}\) is statistically insignificant (P > 0.1) below the surface. This result shows that CaCO₃ may be an important scavenger of Nd in the surface ocean but not at depth. Alternatively, this disparity may be the result of neglecting aqueous speciation when estimating \({K}_{{\rm{d}}}^{i}\), considering that seawater Nd exists mainly as carbonate complex and the carbonate speciation differs between the surface and deep⁵⁹. We are mainly interested in particle scavenging beneath the surface. Thus, we ignore the contribution of CaCO₃ to Nd scavenging in Fig. 1. However, to be comparable with previous reversible scavenging models, we included model sensitivity experiments where we allowed scavenging onto opal and CaCO₃, as discussed later. Finally, we performed an estimation including only oxides and POM. The estimated \({\log }_{10}{K}_{{\rm{d}}}^{i}\) and associated uncertainty of this final analysis are reported in the main text.

Our result of the varying affinity of Nd with particle types are consistent with previous field and laboratory studies. Chemical extractions of the labile proportion of marine particles have REE patterns that resemble that of the Mn oxide^11,63. Aqueous and surface complexation modelling have suggested that in the deep ocean, the dissolved seawater REE patterns are most likely explained by scavenging onto Mn oxide⁵⁹. In contrast, it has long been known that pristine biogenic carbonate contains little REE⁶⁴, and the REE associated with planktic foraminifera are predominantly hosted by oxides attached to the shell rather than within biogenic carbonate⁶⁵. Moreover, sediment-trap studies have found that settling biogenic opal does not contain a resolvable amount of LREE (although it may contain some HREE)⁶⁶. The evidence all points to Mn oxide as the dominant REE scavenger, particularly in the deep ocean, whereas the roles of biogenic carriers, especially carbonate and opal, are negligible.

Pacific cruise

We collected water-column, sediment and porewater samples during the KM2012 cruise (October 2020) onboard R/V Kilo Moana at 3 sites from the equatorial North Pacific along 152° W (Station 3, 11° N, 5,388 m; Station 4, 3° N, 5,050 m; Station 5, 7° N, 5,502 m). Sampling procedures followed ref. ⁴⁴ and are briefly summarized here. Water-column samples were collected and filtered (<0.45 μm) from Niskin bottles on a CTD Rosette. Sediment cores were collected using an MC800 multi-corer and sectioned at 1.2-cm intervals. Porewater aliquots for REE concentration and ε_Nd were collected by centrifuge and filtration (<0.45 μm). The REE aliquots were extracted from one core, and the ε_Nd aliquots combined extractions from corresponding layers of 20 to 25 cores. The REE aliquots include porewater samples from the top 20 cm and all seawater samples from each station, whereas the ε_Nd aliquots are fewer, having only porewater samples from the top 10 cm and the 3 bottom-most seawater samples at each station. Porewater aliquots for nutrient analyses were extracted using Rhizon samplers and filtered (<0.2 µm). Porewater aliquots for dissolved organic carbon (DOC) analysis were extracted via Rhizon, filtered (<0.45 μm with GFF filter), and poisoned with mercuric chloride and stored in a glass vial. Porewater dissolved oxygen (O₂) concentration was measured using a fibre-optic oxygen microsensor inserted into pre-drilled holes through the core into the sediments. The sensor readings were converted to O₂ concentration by linearly calibrating against the published bottom-water O₂ concentration at the study sites. Porewater pH was measured on unfiltered samples using a portable pH sensor post-extraction via centrifugation. Analysis of pH in pore waters is notoriously difficult owing to the changes in pressure upon recovery, and thus the pH data have finite utility. Sediment samples were frozen onboard and freeze-dried in the lab.

Elemental concentrations of the REE aliquots were analysed at Oregon State University using an Elemental Scientific seaFAST-pico offline pre-concentration technique, and the procedure has been extensively documented as part of the GEOTRACES intercalibration effort⁶⁷. Elemental concentrations of the ε_Nd aliquots (approximately 10 ml) were analysed at ETH Zurich using Nobias Chelate-PA1 resin in a manual column procedure⁶⁸. The measured REE concentration and pattern from the two labs agree well (Fig. 2 and Extended Data Fig. 3), and the small differences are expected given that the REE and ε_Nd aliquots represent samples extracted from different cores. The porewater REE concentration of the REE aliquots measured at Oregon State University shows a deep peak between 10 cm and 15 cm, but the scatter in observations of this peak is large among the 3 sites (Fig. 2), despite similarities in the REE pattern between all samples analysed (Extended Data Fig. 3). Unfortunately, the ε_Nd aliquots did not extend to this interval and thus we were not able to confirm this feature at ETH Zurich. While inherently interesting, this deeper peak does not affect our estimation of the benthic flux, which depends on only the REE concentration data at the sediment–water interface. Thus, for the intention of this paper, we have omitted interpretation of this feature. Also, we do not discuss cerium (Ce) in this study, because of the large inter-lab disagreement shown in the GEOTRACES intercalibration effort⁶⁷, and its fractionation from other REE owing to redox sensitivity.

Isotope analysis of the ε_Nd aliquots (about 400–700 ml of pore water or about 1.5 l of seawater) were done at ETH Zurich. Samples were buffered to a pH of 5.5 ± 5 and pre-concentrated using an in-house extraction manifold containing Nobias Chelate-PA1 resin. The procedure has been extensively used for trace-metal isotope analysis at ETH Zurich^69,70. After pre-concentration, separation of Nd from the matrix elements and other REE was done using Eichrom RE and LN spec resins. Ultimately, about 5–10 ng of Nd was available for isotope measurements. Procedural blanks were <3 pg. Isotope analysis was done on a Neptune Plus multi-collector inductively coupled plasma mass spectrometer (Thermo Fisher) following the procedure of ref. ⁷¹. Internally normalized sample data were renormalized to the ¹⁴³Nd/¹⁴⁴Nd ratio of La Jolla⁷². Repeated analysis of 8-ppb La Jolla solutions results in a long-term external reproducibility of 0.27 ε (2σ). Nd isotope analysis was also quality-controlled by repeated measurements of the US Geological Survey reference materials BCR-2 (ε_Nd = −0.11 ± 0.25, 2σ) and BHVO-2 (ε_Nd = 6.70 ± 0.24, 2σ) at the same concentration (about 5–10 ppb) as the porewater samples in agreement with literature results⁷³.

Nutrients were analysed at Oregon State University using a Technicon AutoAnalyzer II (phosphate and ammonium) and an Alpkem RFA 300 (silicic acid, nitrate + nitrite). The method and data processing follow ref. ⁷⁴. DOC was analysed with a V-CSN/TNM-1 (Shimadzu) at the Scripps Institution of Oceanography following ref. ⁷⁵. Sediment samples were analysed for total organic carbon contents using a GVI (now Elementar) Isoprime 1000 with Eurovector EA at Bigelow Laboratory for Ocean Sciences. Samples were measured for the total carbon (organic plus inorganic) and a separate sample split was acidified to remove carbonate and then measured for the organic fraction. Freeze-dried bulk sediments were digested in a concentrated HCl–HNO₃–HF mixture at high pressure, using a microwave-assisted system (CEM MARS-6), and sediment elemental concentrations were measured using inductively coupled plasma optical emission spectroscopy and an inductively coupled plasma mass spectrometer at Oregon State University⁷⁶. X-ray diffraction of freeze-dried raw samples were made at K/T GeoServices, using a Siemens D500 automated powder diffractometer equipped with a Cu X-ray source (40 kV, 30 mA) and a scintillation X-ray detector. Semi-quantitative determinations of whole-sediment mineral amounts were done using Jade Software (Materials Data) with the Whole Pattern Fitting option. Estimation of sedimentation rate was done by radiocarbon dating planktic foraminiferal shells from Station 4 (W. M. Keck Carbon Cycle AMS Facility, UC Irvine), where enough carbonate is available.

Abyssal Pacific sediment

Save for the presence of considerable biogenic carbonates at Station 4 (30% to 73% calcite based on X-ray diffraction) compared with Station 5 (0%) and Station 3 (about 0–1.6%), the sediment mineralogy is similar at all sites, being composed of quartz (about 4–11%), plagioclase (about 3–10%) and illite + mica (about 6–15%), with lesser components of K-feldspar (about 0.7–4%) and chlorite (about 0.7–3%), assuming halite and gypsum reflect dried pore water. There is a large fraction of a semi-quantifiable amorphous phase at all sites (about 40%).

Dissolved oxygen and nitrate + nitrite indicate that aerobic respiration dominates organic-matter remineralization and that diffusion from seawater is sufficient to keep the sediment package oxygenated with no sign of denitrification or more reducing conditions within the upper 20 cm (Fig. 2). Consequently, porewater Fe and Mn was below our detection limits (0.1 μM) in all cores. This diagenetic setting is consistent with previous work in the area⁷⁷. The relatively low organic-matter rain rate⁷⁷ (about 0.1–0.4 mmol m⁻² d⁻¹) combined with aerobic respiration result in low concentrations of particulate (POC, about 0.4 wt% in the mixed layer and about 0.15 wt% below) and dissolved (DOC, about 200–400 μM close to the interface and about 100 μM below) organic matter (Fig. 2).

Authigenic enrichment of metals at the study sites were estimated using detrital correction with Ti assuming that the element/Ti ratio is the same as the upper continental crust⁴¹. Whether using Al or Ti for this correction makes little difference. For example, the estimated mean authigenic Nd concentration is 53 ppm using Al versus 51 ppm using Ti. There is little vertical change of elemental concentrations in the upper-sediment package because of bioturbation. The means of estimated authigenic Nd concentration in the upper 30 cm at Stations 3, 4 and 5 are 49 ± 5 ppm (1σ), 33 ± 7 ppm and 73 ± 9 ppm respectively, and the mean of all samples combined is 51 ± 18 ppm. This inter-site difference is entirely attributed to dilution by biogenic materials (mainly carbonate which is much higher at Station 4). The relative authigenic enrichment of Nd, expressed as the ratio of authigenic to total Nd, is nearly identical at all sites, and the mean ratio of all samples combined is 0.76 (±0.09, a relative standard deviation of about 10% which is comparable to analytical precisions). The result demonstrates a high degree of homogeneity of the authigenic sediments in the study region despite the strong surface-productivity gradient, consistent with biogenic particles contributing little to the particulate REE flux.

REE carriers

Geochemical data of water-column particles and oxide-rich sediment phases were compiled and compared with our abyssal authigenic sediments. The paired particle Nd, Mn and Fe data shown in Extended Data Fig. 1a are available only from the GEOTRACES studies^25,38,60. However, because few sites in the GEOTRACES dataset reported the full REE data, the particle REE data shown in Extended Data Fig. 1c mainly come from other literature sources^{11,63,78,79,80}. In these studies, water-column particulate authigenic REE concentrations were either reported using chemical extraction^11,63, or estimated here using detrital correction based on Al (ref. ⁷⁹) or Th (refs. ^38,78,80), depending on which measurement was available. The Mn–Fe crust and nodule data are from the National Oceanic and Atmospheric Administration and Minerals Management Service Marine minerals geochemical database⁸¹. The data of dispersed Mn–Fe oxides in marine sediments extracted by leaching sediments or foraminifera are compiled by ref. ⁴⁷. The K_d of water-column particles were computed using the estimated authigenic REE concentration and paired seawater dissolved REE concentration from the same study. When computing K_d for crusts and nodules, we used the REE concentrations of our Pacific bottom water to represent deep-ocean seawater in general. When computing K_d for the authigenic sediment, we used the estimated authigenic REE concentrations and bottom-water dissolved REE concentrations from our study sites. Finally, we also compared our data with the Pacific sediment compilation of ref. ⁸² when showing the correlation between Nd and Mn concentrations in abyssal sediments (Extended Data Fig. 1d).

Previous studies have shown that phosphate is also an important host of REE in abyssal sediments^82,83. This observation does not contradict our conclusion that oxides are the main carriers of REE in the water column and surface sediments. As pristine biogenic phosphates contain negligible amounts of REE⁶⁴, the association of REE with phosphates can only happen post-deposition. Studies have demonstrated the diagenetic transfer of REE from oxides to phosphates on the Oregon margin using diagenetic modelling¹⁵, and on the abyssal seafloor using geochemical and mineralogical analysis⁸⁴. Because this kinetic mass transfer is slow on the abyssal seafloor (>10⁴ years according to ref. ⁸⁴), the association with phosphate manifests more strongly in the deeper sediment package, and in regions of lower sedimentation rate⁸³. However, this mass transfer has little effect on the total solid sediment budget, and the total (oxide plus phosphate) authigenic REE burial flux remains similar to that of the oxide-carried particle rain rate¹⁵. For example, a much higher authigenic Nd concentration up to 300 ppm hosted in phosphate-rich abyssal sediments has been found in locations with a much lower sedimentation rate (<0.05 cm kyr⁻¹)⁸³, yet the implied burial rate is <40 pmol cm⁻² yr⁻¹, no more than at our sites and entirely supportable by the Mn oxide-hosted particle rain rate. Thus, we conclude that this diagenetic transfer reconciles the apparent dichotomy that scavenged REE reaching the abyssal seafloor is mainly hosted by Mn oxide, yet in deeply buried sediments phosphate can be the main carrier.

Water-column and sediment mass fluxes

Given the uniformity of authigenic enrichment and detrital mineralogy, we assume that the fluxes of the non-biogenic (detrital and authigenic) materials are similar at the three sites. Our estimation of sediment burial flux uses data from Station 4 where radiocarbon dating is possible. The data here show a bioturbated depth of about 9 cm and a burial velocity of 0.53 cm kyr⁻¹. The burial rate is computed as

where ϕ is porosity (0.85 ± 0.04, 1σ, assuming 5% uncertainty), ρ is sediment grain density (2.65 ± 0.13 g cm⁻³, assuming 5% uncertainty), w is the burial velocity (0.53 ± 0.077 cm kyr⁻¹), and M is the total (42 ± 1 ppm Nd) or authigenic (36 ± 1 ppm Nd) concentration in the mixed layer. Errors are propagated into the results.

To estimate the particle Nd rain rate, we combine the GEOTRACES particle concentration data²⁵ with the Joint Global Ocean Flux Study (JGOFS) particle flux data^85,86,87 based on sediment traps. The rain rate is computed as

where F_p is the particle flux and Nd_p is the total or authigenic Nd concentration in particles. The JGOFS equatorial Pacific traps were deployed along approximately 140° W (15° S–15° N), slightly eastwards of our study sites (152° W, 3° N–11° N). The particle mass flux measured by the traps below 3,000 m at 5° N (between our Stations 4 and 5) is 64 ± 16 mg m⁻² d⁻¹. The GEOTRACES GP16 Station 36 (152° W, 10.5° S) is the closest site with particulate data available that has an oceanographic setting similar to our sites²⁵. The total and authigenic Nd concentrations below 2,500 m (excluding the benthic nepheloid layer) in the sinking particles are 4.2 ± 1.3 ppm and 3.4 ± 1.2 ppm, respectively. The relative enrichment of authigenic Nd in the deep-ocean particles (about 80%) is similar to that in our abyssal sediments (about 76%).

Diagenetic model

We performed diagenetic modelling using SedTrace⁸⁸, a tool that automates the generation and simulation of trace-element diagenesis. The diagenetic equations of biogeochemical tracers and REE have been reported in our previous study of REE diagenesis on the Oregon margin¹⁵ as well as in the model description paper of SedTrace⁸⁸. The model includes the following biogeochemical tracers: POC, DOC, CaCO₃, O₂, NO₃, NH₄⁺, TCO₂ and H⁺. POC is modelled using a 2-G model, including a labial component (POC₁) and a refractory component (POC₂) suggested by previous works in the study region⁷⁷. We assumed that the POC components are first converted to DOC (DOC₁ and DOC₂ respectively), which subsequently undergo aerobic remineralization⁸⁹. We also included nitrification and carbonate dissolution in the model¹⁵. The pH model follows the standard construction in SedTrace⁸⁸.

The biogeochemical model is tuned to fit the average sediment biogeochemistry represented by Station 5 (Fig. 2). To capture the high concentration of DOC at the sediment–water interface (Fig. 2d), the labial DOC₁ (Extended Data Fig. 2b) needs to be a high-molecular-weight compound with low molecular diffusivity⁹⁰ relative to the refractory DOC₂, consistent with the conceptual model of POC remineralization in marine sediments⁸⁹. Because the abyssal sediment is poorly buffered, modelled pH decreases from 7.7 at the sediment–water interface to 7.2 at 20 cm, qualitatively consistent with the measured values (about 7.2–7.3 at Station 5, although we note the limited utility of this data because of the sampling issue mention above; Extended Data Fig. 2c).

Three processes affect porewater REE in the model: complexation with dissolved ligands, release during POM remineralization and sorption onto oxides. Complexation of REE with inorganic ligands and the related stability constants follow that of refs. ^59,91. We also include REE complexation with the two types of DOC, and the stability constants are tuned within the range of organic ligands reported in literature⁹² (Extended Data Fig. 3c). To model Nd by POM remineralization, we derive a reasonable estimate of the Nd/C ratio released by POM. We start from the water-column K_d of POM estimated above, and find a value that is consistent with this K_d and reasonably fits the porewater Nd profile. The release of the other REE is scaled to Nd, the REE pattern of which is tuned following the pattern of K_d of POM reported in the literature^93,94,95 (Extended Data Fig. 3b). Finally, we implement pH-dependent sorption of REE onto Mn–Fe oxides following refs. ^59,96,97, which was derived using laboratory adsorption experiments using synthetic oxides in ionic media similar to seawater. We assume that only the free REE ions are adsorbed, and use the pH-dependent free-ion-based \(\genfrac{}{}{0ex}{}{{\rm{f}}}{}{K}_{{\rm{d}}}\), which is related to the total concentration-based K_d:

where ^fα is the fraction of free ion. K_d is an apparent constant that depends on the speciation of REE. We estimated \(\genfrac{}{}{0ex}{}{{\rm{f}}}{}{K}_{{\rm{d}}}^{{\rm{N}}{\rm{d}}}\) using the \(\genfrac{}{}{0ex}{}{}{}{K}_{{\rm{d}}}^{{\rm{N}}{\rm{d}}}\) derived from the GEOTRACES particle data and seawater speciation results, and found that it is about three orders of magnitude higher than the experimental values measured using synthetic Mn–Fe oxides in the lab, a known discrepancy⁹⁸ that is likely attributed to the difference in the surface chemistry between natural and synthetic oxides and the uncertainty in the aqueous speciation of REE in seawater⁵⁹. In an ad hoc approach, we used the lab-based REE pattern of \(\genfrac{}{}{0ex}{}{{\rm{f}}}{}{K}_{{\rm{d}}}\) in the model, but scaling them such that the value of \(\genfrac{}{}{0ex}{}{{\rm{f}}}{}{K}_{{\rm{d}}}^{{\rm{N}}{\rm{d}}}\) is consistent with the field data. That our model can successfully reproduce the porewater data REE pattern suggests that although the lab-based values of synthetic oxide \(\genfrac{}{}{0ex}{}{{\rm{f}}}{}{K}_{{\rm{d}}}\) may not apply to natural oxides, their REE pattern appears like natural oxides. This implies that the discrepancy is caused by factors common to all REE, and thus most likely related to particle surface chemistry rather than REE speciation. To model porewater ε_Nd we added ¹⁴⁴Nd and the radiogenic ¹⁴³Nd as two individual tracers to the model¹⁵, both of which are subject to the same processes.

The decrease of pH reduces \(\genfrac{}{}{0ex}{}{{\rm{f}}}{}{K}_{{\rm{d}}}\), whereas the increase of organic ligand concentration lowers ^fα, thus decreasing K_d in sediment (Extended Data Fig. 2d), promoting relative desorption of REE from Mn–Fe oxides. Modelled REE speciation is shown using Nd and Lu to represent LREE and HREE, respectively (Extended Data Fig. 2e,f). K_d computed using equation (5) is shown in Extended Data Fig. 3a where the ribbon indicates the range of K_d in the sediment package. Modelled porewater REE patterns are shown by normalizing to either the local bottom water or Post-Archaean Australian Shale (PAAS) (Extended Data Fig. 3).

Benthic fluxes

The benthic flux of REE is calculated as:

where i is the index of REE species, including the inorganic species and complexes with DOCs, \({D}_{{\rm{sw}}}^{i}\) is the molecular diffusivity and ∂Cⁱ/∂z is the concentration gradient. The benthic flux is computed by summing over the individual species because the organic and inorganic ligands have different molecular diffusivity⁸⁹. This calculation is straightforward in the model as the individual species are modelled directly. For data-based estimates, we distinguish the low-diffusivity DOC₁ from the other species that have the same diffusivity in the model. The porewater concentration profiles of REE can be considered as the superposition of a shallow peak (DOC₁ complex) onto a slowly increasing background (DOC₂ and inorganic species) concentration. We use the concentration immediately below the shallow peak to represent the background concentration, and the concentration of the DOC₁ complex is calculated by subtracting the background from the measured profiles. ∂Cⁱ/∂z was then computed using the decomposed profiles. Given the small role of DOC₁ complexation in the speciation of LREE, Nd is negligibly affected by this decomposing compared with HREE Lu. The data-based estimate was done using the mean concentration profile averaged over the three sites, and the errors are propagated throughout the calculation to give an overall estimate of benthic flux and its uncertainty in the study region.

Aside from measured and modelled benthic REE fluxes, in Extended Data Fig. 3 we also show the following sedimentary fluxes: data-based total sediment and authigenic REE burial fluxes, and POM-associated REE rain rates used in the model.

Water-column model

We model the 3D distributions of Nd concentration using the transport matrix method^34,99:

where Nd_T is the total Nd concentration, and the dissolved (Nd_d) and scavenged Nd (Nd_s) are computed using equation (1) assuming reversible scavenging; T_c and T_w are the transport matrices for 3D ocean circulation and vertical particle sinking respectively; and F_river, F_dust and F_benthic are the per volume sources of Nd due to river input, dust deposition and benthic flux, respectively. Other sources are considered minor and not included^9,13,34,100. We create and solve the steady-state model using the Julia language package AIBECS.jl⁹⁹, which is similar to the popular AWESOME OCIM framework of ocean biogeochemical modelling¹⁰¹. Our model is inspired by previous models of marine Nd cycles^3,13,100,102, especially GNOM³⁴, but diverge from them in the implementation of the particle scavenging and benthic fluxes, as described in this study. We give a brief description of our model construction and experiments here.

The Ocean Circulation Inverse Model (OCIM)^43,103 has been widely used as the circulation matrix T_c in OBMs of trace elements^34,101. Here we use the OCIM2-48L version (2° horizontal resolution, 48 vertical layers), which updates the previous versions by adding more depth layers and implementing bottom-intensified mixing following the state-of-the-art parameterization of ref. ¹⁶. The result is a better representation of the abyssal Pacific circulation strongly shaped by seafloor topography⁴³, making this model version ideal for studying the bottom-up control on the marine Nd cycle.

Dissolved, scavenged and total Nd concentrations are related via K_d (equation (1)). In our model, we only include biogenic particles and MnO₂. We obtained a 3D field of POM from previous OBMs¹⁰¹ and mapped it onto the model grid. We obtained 3D fields of carbonate and opal concentrations using satellite-derived surface export flux and depth-dependent attenuation laws following previous models (remineralization length scales were set to 3,500 m for carbonate and 10,000 m for opal)^13,104.

We currently lack a faithful reconstruction of the 3D field of MnO₂ by OBMs owing to the challenge of modelling the marine Mn cycle⁵⁴. Instead, we use an artificial neural network (ANN) to interpolate the GEOTRACES particle data (IDP 2021 Version 2)³⁸ onto our model grid, as previous studies have done for other ocean biogeochemical fields^31,105. The data are mainly from the Pacific (GP16) and Atlantic (GA01, 03, 06), with minor contributions from Arctic (GN01, 02, 03) and Southern Ocean (GA10) cruises. This ANN is a perceptron consisting of 2 hidden layers with 50 neurons and rectified linear unit activation function. We train with the following predictors: sampled water depth and latitude; temperature, salinity, oxygen, phosphate and silicate concentrations from World Ocean Atlas⁵⁶; mixed-layer depth, Δ¹⁴C, POM concentration and ³He/⁴He ratio from previous OCIM studies^43,101,103; and transmissometer-derived nepheloid-layer particle concentration^101,106. These predictors are selected to account for potential locational, physical and biogeochemical factors controlling the distribution of MnO₂, as well as the influence of a hydrothermal source and sediment resuspension. The gridded data products of these predictors are interpolated at the GEOTRACES sample locations and model grid points. We randomly selected 80% of the data from each ocean basin to create a training dataset, and the residual 20% was used for testing. In this way, the ANN results are less biased towards any individual ocean basin. Such data partitioning was repeated to generate a 500-member ensemble. We trained the ANN with the Adam optimizer and L₂ regularization using the Julia machine-learning package MLJ.jl¹⁰⁷. The model misfit generally stops changing after about 50 epochs, and we terminate the training after 100 epochs. The correlation coefficients between the predicted and observed MnO₂ are 0.92 and 0.90 (in the log-transformed space) for the training and testing sets, respectively (Extended Data Fig. 6). The root mean square errors are 0.25 µg l⁻¹ for both sets. The generated MnO₂ field correctly captures the main features in the GEOTRACES observation³⁸ including, for example, the hydrothermal plume, nepheloid layers and oxygen minimum zones in the Pacific GEOTRACES transect GP16²⁵, and the strong benthic nepheloid layer in the Northwest Atlantic^60,106 (Extended Data Fig. 6).

The river discharge in the model is derived from a global discharge model¹⁰⁸, and the river dissolved Nd concentration is from the observational dataset of ref. ¹⁰⁹. We assume a 30% removal of river Nd flux in the estuary^9,110. Dust depositional flux in the model is derived from a global dust model¹¹¹. We assigned a dust Nd concentration of 27 ppm (similar to the upper continental crust) and solubility of 2%, as in previous models^9,13.

We treated the benthic flux per unit area as a function of water depth (Fig. 3e) and tuned it within the range of the observations in the model experiments. The published benthic flux data are derived using porewater profiles^44,68 and generally consider only the diffusive fluxes, which may underestimate the total benthic flux by ignoring other transport mechanisms such as bio-irrigation and advection^15,68. Ocean models, even the improved OCIM2-48L, generally cannot entirely capture ocean bathymetry owing to limited resolution. We use the ETOPO 2022 global relief model to derive a subgrid bathymetry that better captures the distribution of the area-to-volume ratio in the real ocean⁹⁹, and allows the conversion of benthic flux per unit area to benthic flux per unit volume (Fig. 3e,f and Extended Data Fig. 7).

Through sensitivity tests (Fig. 3 and Extended Data Figs. 4 and 5), we evaluated the potential impact of particle scavenging and benthic flux on the distribution of Nd concentration in the Pacific. In the first experiment, we do not consider benthic flux and only include POM as a scavenger. We use a K_d of 10^5.8 for POM, within the range of our data-derived values, and a settling velocity of 2.0 m per day similar to Th-based estimates^{2,112,113,114,115}. Although our analysis of the GEOTRACE particle data do not support opal and carbonate as important Nd scavengers, we still chose to perform model tests to be comparable with previous reversible scavenging models. In these tests, we set the K_d to 10^7.0 and 10^5.6 for opal and carbonate, respectively, and these values were chosen to fit the surface Nd concentrations (Extended Data Fig. 4). In the second experiment, we further added MnO₂ scavenging with a K_d of 10^8.7 (Extended Data Fig. 6), according to our data-derived value, while keeping other parameters the same. In the last experiment, we further added a benthic flux while keeping other parameters the same. We used a vertical profile of benthic Nd flux per area that is consistent with observations, which is converted to flux per volume using the seafloor-area-to-volume ratio in the model subgrid bathymetry (Fig. 3e,f and Extended Data Fig. 7).

The model equation for radiogenic ¹⁴³Nd is similar to that of total Nd (equation (9)), except that the sources on the right-hand side are converted to sources of ¹⁴³Nd according to their isotope compositions. We obtain the ε_Nd of river input according to the gridded continental rock ε_Nd dataset of ref. ¹³. We map the ε_Nd of dust based on dust provenance^13,111.

Previous studies often used the gridded global sediment detrital ε_Nd map⁹ to represent benthic flux ε_Nd. However, it is well recognized that detrital sediment ε_Nd do not always represent the ε_Nd of benthic flux^9,13,33,47, which is sometimes dominated by a small fraction of reactive detritus, such as volcanic materials in the Pacific^14,15,33. Consequently, such models have difficulty in explaining Pacific seawater ε_Nd data¹³. Other studies have attempted to modify the detrital ε_Nd map to solve this problem³⁴, but such modifications are generally arbitrary, and not constrained by studies of sedimentary Nd cycling.

Here we parameterize the benthic flux ε_Nd following our present and previous^{8,15,33,47,116} observational and modelling studies of sediment diagenesis. In the Pacific, we partition the benthic flux used in the Nd concentration model above into a recycled component and a new component. The ε_Nd of the recycled flux is set to be the same as seawater ε_Nd at the bottom-most water-column grid above the seafloor. The ε_Nd of the new flux is set to be pure volcanic (+10 ε). We use this value for sedimentary volcanics as a starting point for our sensitivity test. Our model choice of the proportion of the new source (0–30%) was based on porewater and authigenic sediment data^15,116 (Fig. 4b). If we set the new source ε_Nd to lower (higher) values, the porewater and authigenic sediment data would simply require a greater (lower) proportion of the new source, but the net effect of the new flux would remain the same. There is no observational study of benthic flux ε_Nd in other ocean basins, so outside of the Pacific we set the benthic flux ε_Nd to be the same as detrital sediment ε_Nd compiled by ref. ⁹ (Extended Data Fig. 8). Previous research has shown that using detrital ε_Nd to represent benthic flux ε_Nd works reasonably well in the other basins¹³. Our model results that the Southern Ocean ε_Nd can be reproduced (Fig. 4) shows that this approach is adequate given our focus on the Pacific Ocean, and we leave the study of benthic fluxes for the future.

In a set of sensitivity tests, we set the new component to be 0%, 10%, 20% and 30% of total benthic flux, respectively (Extended Data Fig. 9). We use the modelled total Nd concentration from the third experiment in the concentration sensitivity test (Fig. 3b). We model the concentration of radiogenic ¹⁴³Nd, and compute the ε_Nd letting ¹⁴³Nd and ¹⁴⁴Nd sum to the modelled total Nd.

We also tested model sensitivity to where the new benthic flux is applied. In the test shown in Fig. 4, the new flux is added to all seafloor areas in the Pacific. In Extended Data Fig. 10a–c, we limit the new benthic flux to the margins up to water depths of 1,000 m, 2,000 m and 3,000 m, respectively. In Extended Data Fig. 10d–f, we restrict the new flux to the abyssal seafloor below 3,000 m, either in the entire Pacific, or only in the South Pacific, or everywhere except the dust province in the North Pacific where detrital sediment is predominantly composed of Asian dust⁴⁸. The areal extent of the North Pacific dust province is delimited by the contour of detrital sediment ε_Nd of −8 (Extended Data Fig. 8).

Finally, we model the water-mass age (that is, ideal age) following the original OCIM2_48L study⁴³. The modelled circulation age is used to show the impact of benthic exposure time³³ on the distribution of seawater ε_Nd.

Bottom-intensified mixing

The diapycnal diffusivity κ_ρ in Extended Data Fig. 7c is computed using the state-of-the-art parameterization of topographic mixing driven by internal tide dissipation from ref. ¹⁶, which has been validated against microstructure observations. The horizontal mean depth profile is:

where B is buoyancy flux, N is buoyancy frequency, ε is turbulence production and ⟨⟩ denotes these are horizontally averaged. The diapycnal diffusion length of Nd is then:

The diffusion length L_Nd (Extended Data Fig. 7d) should be interpreted as the length scale that a source of Nd can be of influence by turbulent diffusion alone in the water column on the timescale of Nd residence time (τ_Nd). Literature reports of τ_Nd are in the range of about 350–750 years^{3,9,34,44,102,117}, and we use a value of 400 years as a first-order estimate.

Nd data compilation

We compiled literature data of seawater, core-top authigenic and detrital sediment ε_Nd, and seawater Nd concentration previously⁹, which is updated here to include recent GEOTRACES results^23,38,118 (Extended Data Fig. 8). The paired authigenic and seawater data shown in Fig. 4b were created by binning the Pacific data into boxes that have 10° latitudinal, 20° longitudinal and 300 m (about 0–1,500 m) or 1,000 m (below 2,000 m) vertical resolutions. Data that fall into the same box were averaged and the standard deviations are reported (Fig. 4b).

We also compiled Nd concentration data in organic-rich sediments from the literature^{55,116,119,120,121} to complement other trace-metal data from ref. ⁴⁹, shown in Fig. 5d.