A population code for spatial representation in the zebrafish telencephalon

Experimental set-up

Simultaneous behavioural and neural imaging by tracking microscopy

Tracking microscopy was performed as described in our previous study⁷. Motion cancellation was performed by a custom three-axis motorized system, to be described elsewhere (Mohan et al., manuscript in preparation). To enable animal tracking, the behavioural chamber is illuminated by four custom light strips consisting of narrow-angle, 850 nm infrared light-emitting diodes (LEDs; no. SFH4655-Z, Osram) that deliver infrared light to the chamber by total internal reflection. Ambient white-light illumination in the behavioural chamber is provided by an array of wide-angle white LEDs (no. GW PSLM31.FM).

For recording of neural activity, we used DIFF microscopy to image a brain area of 1,013 × 764 × 150 µm³ at cellular resolution, a volume rate of 2 Hz and frame rate of 200 Hz, as described in our previous study⁷. The performance and characteristics of the imaging system have been characterized in depth in our previous study⁷.

Chamber construction and experiment design

Several constructions for the chamber wall were used depending on the complexity of the experiment. The top and bottom of all behavioural chambers are made of glass to allow optical access from above and below⁷. Between the glass plates, 1-mm-thick, gas-permeable PDMS walls (Sylgard 184, Dow Corning) were used to create a watertight rigid body as described previously⁷. PDMS chambers were cut using a computer-controlled blade and finished by manual cutting. The chamber was filled with E3 water before fish loading (‘Fish loading, removal and reloading’). Following fish loading we gently closed the chamber by sliding on a top coverslip. Excess fluid was removed to create a watertight seal between the PDMS and the two glass surfaces. Each imaging session lasted 45–100 min to ensure sufficient spatial coverage of the arena (each experiment is described in more detail below). We did not include any fish in our analysis that was quiescent for more than 20 min during the experiment. If not specified explicitly, all chambers were initially new to the fish.

For whole-chamber-rotation experiments (Fig. 4m) and rectangle-to-circle experiments (Fig. 6a), the outer wall (1 mm thick) is made of translucent white PDMS cut into the desired chamber shape. Landmarks are constructed from black PDMS pieces embedded into the outer wall. A clear PDMS inner wall (0.5 mm thick, 1.5 mm wide) placed alongside the outer wall prevents the fish from direct interaction with the outer wall or landmarks. For chamber-rotation experiments, animals were first imaged for 90 min in the rectangular chamber (S1) and then the entire chamber was slowly rotated over 10–20 s as a rigid body without removing the animal (that is, the chamber walls, ceiling, floor and fish all rotated together). Animals were then imaged for a further 60 min (S2).

For experiments that required rotation of the chamber wall without removal of the animal or disassembly of the chamber (Fig. 5m), an outer PDMS wall with a central square cut-out of 60 × 60 mm² was used only for water-sealing the chamber. An inner chamber wall (of distinct size and shape from the outer PDMS wall) was constructed from laser-etched plastic with embedded stainless steel pieces (grade 430), which enabled remote repositioning of the plastic chamber wall using small magnets (3–5 mm in diameter) below the bottom glass of the chamber. Landmarks (when used) were painted onto the wall of the plastic chamber. The plastic chamber wall was placed inside the square cut-out of the outer PDMS wall. Animal movement was restricted to within the plastic chamber walls. Given the flexibility of this chamber design, we also used it for the experiments shown in Fig. 5a,e,i and Extended Data Fig. 9a.

In the wall-rotation experiments we first recorded the animal for 45–90 min (S1) and then the entire chamber assembly was removed from the microscope. Using small magnets underneath the bottom glass of the chamber, we then carefully rotated the chamber walls by 180° before replacing the chamber assembly on the microscope. During this manipulation only the walls rotate but not the fish. Following wall rotation the animal was recorded for a further 45–75 min (S2).

For wall-morphing experiments (Fig. 4i) we constructed a morph chamber consisting of eight pieces of stainless steel (12 × 2 × 1 mm³) linked by a flexible ring of silicone (1 mm wide and 0.5 mm tall). The stainless steel pieces can be remotely repositioned using small magnets below the bottom glass of the chamber (as described above), allowing flexible and gradual morphing of the chamber wall. As described above, an outer PDMS wall with a central square cut-out of 60 × 60 mm² was used only for water-sealing the chamber, and the morph chamber was placed inside the square cut-out. Animal movement was restricted to within the morph chamber. We first arranged the morph chamber into a radially near-symmetric octagon and recorded the animal for 45–65 min (S1). Using small magnets underneath the bottom glass of the chamber, we then morphed the chamber wall into an ellipse. During this manipulation we ensured that the walls did not make strong physical contact with the fish. Following morphing, the animal was recorded for a further 45–70 min (S2).

For border-insertion and -removal experiments (Extended Data Fig. 3b) we used a PDMS chamber with an 84 × 15 mm² central cut-out in which the animal was free to move. At the midpoint of the long axis of the chamber we created a hidden rectangular pocket (21.5 × 2 mm²) containing a stainless steel rectangular bar (20 × 1.5 × 0.5 mm³). Using a small magnet, the stainless steel bar can either be inserted into the chamber (creating an extra border wall) or hidden from the chamber. In S1 (45–95 min) the movable wall was hidden from the animal. Following S1, the movable wall was inserted into the interior of the chamber and the animal recorded for 45–95 min (S2). Following S2, the movable wall was again retracted and hidden from the animal, and the animal recorded again for 45–90 min (S3).

For the landmark-removal experiment (Fig. 4e) we used a PDMS chamber with a 25 × 25 mm² central cut-out. On one edge of the chamber we created two additional PDMS pockets (100 × 2.5 mm²) that each contained a 70 × 2 × 0.5 mm³ white (acrylic painted), stainless steel, rectangular bar. Landmarks (vertical black stripes) were painted on a portion of one of the stainless steel bars (Fig. 4e) whereas the opposing stainless bar was completely white. In S1 (75–90 min), landmarks were positioned so as to be visible to the fish. Following S1, by applying small magnets to the bottom glass of the chamber, the stainless steel piece with landmarks was remotely moved into the PDMS pocket, effectively hiding the landmarks from the animal within the chamber; the opposing stainless steel bar was not moved. The animal was then recorded again for 60–100 min (S2).

Fish loading, removal and reloading

For all experiments, fish were loaded into the chamber using a glass or plastic pipette. For experiments with fish removal between S1 and S2 (Figs. 5a,e,i and 6a) we used the following procedure. Following the first 60–90 min recording (S1) the chamber was removed from the microscope. The top coverslip of the chamber was loosened and then either partially or completely removed. The fish was then removed from the chamber with a glass or plastic pipette. In between sessions, the chamber was thoroughly cleaned with soap and isopropanol and then pressure-rinsed for 2–5 min. For two fish (Extended Data Fig. 8g) we rotated the bottom glass relative to the chamber walls without cleaning, to scramble any potential olfactory cues. We reloaded the fish into the chamber at a different heading and position from those at which the animal was removed. Following fish loading, the chamber was again sealed with its top glass coverslip and transferred to the microscope for a second imaging session (45–100 min). For the ABA experiment (Extended Data Fig. 9a) the same procedure was carried out to load the fish into the B chamber for S2, and to subsequently load the fish into the A chamber for S3.

Lights-on/off experiment

To study how PFs are influenced by the luminance of the environment we designed a light/dark protocol. Following 60 min of recording fish exploring the circular PDMS chamber we turned off the white LEDs, providing visible illumination to the chamber. Turning off the white LEDs resulted in a luminance change from 7.05 to under 0.01 µW mm^−2, measured at the centre of the chamber. To ensure that the transition to lights off did not generate an aversive response, luminance was changed gradually over 1 min. Recording was then resumed for an additional 60 min.

We note that a small blue spotlight with a radius of 0.5 mm is always centred on the brain of the fish under all conditions, due to its requirement for neural imaging. We measured the light scattering from this spotlight to be 0.14 µW mm^−2 within 5 mm of the source.

Light intensity measurements were performed using a photodiode-based optical power sensor with a known detector area (no. S130C, Thorlabs).

Image registration

High-resolution offline registration of fluorescent brain volumes for each animal

Each fluorescent image from the tracking microscope was registered to a high-resolution reference brain volume collected from the same animal. An in-depth description and characterization of the registration pipeline was published in our previous study⁷. Briefly, an initial coarse registration is obtained by optimization of a three-dimensional rigid transformation that maps the moving image to a (possibly tilted) plane within the reference brain volume. This planar surface is then finely subdivided into a deformable surface that is locally adjusted within the reference volume using a regularized piecewise affine transform.

Registration to a common reference brain across animals

We use the Computational Morphometry Toolkit (CMTK)⁵¹ to register each animal to a common reference fish. An atlas fish⁵² was selected to serve as the common reference brain. Each brain was registered onto the reference brain in a series of steps: initialization, rigid, full affine, warp. The coordinate transformation for each individual cell was then saved. The command line commands are listed below:

cmtk make_initial_affine –centers-of-mass moving_image fixed_image initial.list

cmtk registration –initial initial.list –nmi –dofs 6 –dofs 12 –nmi –exploration 8 –accuracy 0.8 -o affine.list moving_image fixed_image

cmtk warp –nmi –threads 160 –jacobian-weight 0 –fast -e 18 –grid-spacing 100 –energy-weight 1e-1 –refine 4 –coarsest 10 –ic-weight 0 –output-intermediate –accuracy 0.5 -o warp.list affine.list

cmtk reformatx –pad-out 0 -o out_image –floating fixed_image moving_image warp.list

cmtk streamxform warp.list <cell_coordinates.txt > cell_coordinates_registered.txt

Image analysis

Extraction of neural activity by NMF

Non-negative matrix factorization (NMF) separates each cell into two components—a spatial footprint and a time-varying activity component—as described in our previous study²⁷. Briefly, following registration, we applied constrained NMF³² to our whole-brain datasets with nuclear localized fluorescence. NMF was performed for each axial section of a given brain volume. Our axial sections of the reference volume are separated by 2 µm and the average diameter of a zebrafish cell is approximately 5 µm; thus there can be double counting of centroids if a cell spans more than one axial plane. Cell centroids were detected throughout the entire reference brain volume but were included in downstream analysis only if they were sampled in at least 30% of time points throughout the imaging session. We merged these cell centroids belonging to the same cell based on close spatial proximity (horizontal distance 1.4 µm or less, vertical distance 2 µm or less) and highly correlated activity (over 0.7). Following merging, the number of cells was 73,621 ± 10,558 (mean ± s.d.), decreasing by 28.4 ± 2.6% (mean ± s.d.) across animals (n = 6 fish).

The fluorescence baseline for each merged cell was estimated using the tenth percentile within a 30 min sliding window. Baseline-corrected fluorescent traces ΔF(t) were then obtained by subtraction of the estimated baseline from raw fluorescent traces.

Identification of PCs

For identification of PCs we first generate a spatial activity map for each neuron (see below), use this map to compute spatial information and specificity⁸ (see below), generate shuffled data by circular permutation to obtain a null distribution for spatial specificity (see below) and, finally, compare the spatial specificity of each cell to the null distribution from shuffled activity and to the distribution of spatial specificity across the brain (see below). The spatial information/specificity criteria for PC identification were originally defined by Skaggs et al.⁸. The criteria we use are similar to those in the existing literature in both mammals and birds, for both electrophysiological and calcium imaging data^16,53.

A spatial activity map was generated for each neuron, representing the mean neural activity at each spatial location. To calculate the spatial activity map the chamber was divided into square bins (side length 1.2 mm) and then the summed neural activity and occupancy time were calculated for each bin. This resulted in two matrices: a summed neural activity matrix and an occupancy matrix (matrix entries correspond to spatial bins). We then applied a boundary-constrained Gaussian filter (standard deviation one bin, with the boundary defined by the chamber boundary) to these two matrices. The spatial activity map was calculated by dividing the filtered summed neural activity matrix by the filtered occupancy matrix to obtain the filtered average activity in each spatial bin. When the fish was stationary (speed below 0.1 mm s^−1), the corresponding frames were not included in the calculation of the spatial activity map. For all experimental spatial activity maps (for example, for comparison of spatial maps across sessions) we exclude the first 15 min following initial exposure to the environment in S1. For within-session control (comparison between the first and second halves of S1) we separately generated spatial activity maps for the first and second halves of S1. The first 15 min were not excluded in the within-session control, to ensure sufficient coverage of the environment by the fish trajectory.

From the spatial activity map of each cell, spatial information can be used to quantify how much information is contained by that cell about the location of the animal, in units of bits per second⁸. For each cell, spatial information I was calculated as

where x is a spatial bin, P(x) is the probability that the fish is in spatial bin x, λ(x) is the mean activity of the cell when the fish is in spatial bin x and λ is average neural activity, computed as \(\lambda ={\sum }_{x}\lambda (x)P(x)\).

Based on the equation above, cells with high average neural activity tend to have higher spatial information. To normalize for this we calculate specificity s as

In other words, specificity is spatial information divided by average neural activity, resulting in units of bits per activity unit.

Due to our baseline correction, bins occasionally have negative average activities. Such bins, as well as those with less than 1 s total occupancy time following Gaussian filtering, were not included in the calculation of spatial information and specificity.

To test the significance of the specificity of each cell we use circular permutation to construct a null distribution. For each cell we define the set of valid timepoints as the frames in which neural activity was recorded and fish movement speed was above 0.1 mm s^−1. A null distribution for specificity is then estimated by measurement of specificity after circularly permuting the neural activity vector within the valid time points by 1,000 offsets (each offset is 0.5 s, so it covers from −250 to +250 s). The specificity of a given cell is converted to a specificity z-score by subtracting the mean specificity of the null distribution and dividing by the standard deviation of the null distribution. To test the significance of the specificity of a cell at the population level, a population specificity z-score is also calculated by subtracting the mean specificity of all recorded cells and dividing by the standard deviation of the specificity of all recorded cells.

To be classified as a place-encoding cell, a cell is required to have a specificity z-score larger than or equal to 5, a population specificity z-score larger than or equal to 3 and a specificity value of over 0.01 bits per activity unit.

Defining place fields

The place field (PF, or firing field) of each neuron is defined as the set of spatial bins with activity above 80% of peak activity (with peak defined as the 95th percentile) of the spatial activity map. A more in-depth and systematic analysis of unimodal and multimodal PFs is described in Extended Data Fig. 1i–k, in which the activity threshold was swept from 50 to 80%. The location of the PF is represented by its COM for cells with a single PF. For cells with multiple PFs (as distinct components in the map) we use the COM of the component (over 20 bins, to avoid spurious PFs due to noise), with the highest peak activity (defined as the 95th percentile of the component) as the location of its primary PF. Only PCs with a PF size of less than 30% of chamber size are included in maps of the distribution of PFs and in the analysis of PF shift. PFs are used only for analysis of PF shift and visualization of PF location across an environment. All other analyses of PC activity, such as PF correlation, PV correlation, change in specificity and positional decoding, use the spatial activity map directly.

Rigid and non-rigid registration of spatial activity maps across sessions

Experiments were conducted with various chambers, sometimes in varying orientations, sometimes before and after morphing the chamber into different shapes. For comparison of spatial activity maps across these chambers we developed methods to register maps across sessions. When there was no change in chamber wall geometry (for example, whole-chamber rotation), registration was performed by rotation and translation of the S2 activity map (that is, a rigid transformation) so that activity in both sessions was represented in terms of the spatial bins of S1, thus facilitating comparisons (‘PV correlation, PF correlation and PF shift’).

Otherwise we performed non-rigid transformation to register spatial activity maps across sessions. Our strategy was first to establish a correspondence between the chamber walls of both sessions, then to map each spatial bin of S2 to a set of spatial bins in S1 according to their distance to the wall anchor points, and finally to represent the activity of S2 in terms of the spatial bins of S1. Each of these steps is described in greater detail below.

First we detected the walls of the chambers in both sessions and defined a set of anchor points on the chamber walls. Because the precise number of detected wall points could differ between sessions, we used linear interpolation to upsample the wall points of the session with fewer points, such that the number of anchor points was the same across sessions. The correspondence between anchor points across sessions was established based on either landmarks (for example, the wall-morphing experiment with fish removal; Fig. 5i) or the polar angle of the wall within the microscope reference frame in experiments with no clear match between geometry or landmarks (for example, rectangle-to-circle remapping (Fig. 6a) and ABA remapping (Extended Data Fig. 9a)), or by systematic consideration of every rotation of the anchor points in S2 relative to S1 (Extended Data Figs. 8c,d and 10; ‘Non-rigid transformation with the best rotation angle’).

Next, for each spatial bin centre (x,y) in S2 we compute a corresponding location \(({x}^{{\prime} }\,,{y}^{{\prime} })\) in S1 using a COM procedure. Specifically, for each anchor point \(({x}_{a},{y}_{a})\) in S2 we associate a weight \(1/{d}^{2}\), where d is the distance between the anchor point \(({x}_{a},{y}_{a})\) and the spatial bin centre (x,y) in S2. We then use the previously established wall correspondence between both sessions to transfer these weights to the anchor points in S1. The corresponding location \(({x}^{{\prime} }\,,{y}^{{\prime} })\) in S1 is then defined as the COM of the S1 anchor points (that is, the weighted sum of the S1 anchor points divided by the sum of the weights).

Finally we represent the activity of S2 in terms of the spatial bins of S1. The computed location \(({x}^{{\prime} }\,,{y}^{{\prime} })\) in S1 is generally between the spatial bin centres of the S1 activity map, so we identify the 4 × 4 spatial bins with bin centres (x,y) with \({\rm{floor}}({x}^{{\prime} })-1\le x\le {\rm{ceil}}\,({x}^{{\prime} })+1\) and \({\rm{floor}}(\,y)-1\le y\le {\rm{ceil}}\,(\,y{\prime} )+1\). In this way we associate each S2 spatial bin with 4 × 4 spatial bins in S1. This procedure ensures that each S1 spatial bin is associated with at least one S2 bin. We then average the activity of all S2 bins that are associated with a given spatial bin in S1, yielding a representation of the activity of S2 in terms of the spatial bins of S1.

Non-rigid transformation with the best rotation angle

Non-rigid transformation of the S2 maps described above is generally applied assuming a rotation angle of 0° between sessions (for example, Figs. 4i, 5i and 6a). For systematic investigation of whether a coherent map rotation had occurred between sessions (Extended Data Fig. 8d), 72 incremental rotations (covering 360°) were applied to the S2 anchor points followed by non-rigid registration as described above. The best rotation angle is identified by the maximum PF correlation (‘PV correlation, PF correlation and PF shift’) across sessions. We refer to this procedure as ‘non-rigid transformation with the best rotation angle’. Note that this is also done for the early–late control in Extended Data Fig. 8c,e.

To test whether the improvement in PF correlation, from ‘non-rigid registration assuming an angle of 0°’ to ‘non-rigid transformation with the best rotation angle’, is significant, we shuffle the cell identity in S2. Post shuffle, we then compare the improvement in PF correlation from non-rigid registration assuming an angle of 0° with non-rigid transformation with the best rotation angle. This was repeated 1,000 times to generate a null distribution. The P value in Extended Data Fig. 10 is calculated by counting the percentage of shuffles in which the real data improve by less than the shuffle control.

PV correlation, PF correlation and PF shift

For comparison of population-level activity across sessions, a population vector correlation (that is, PV correlation) was computed for each spatial bin that is shared across sessions. For each neuron we first compute a ΔF/F spatial activity map for each session. To do this we estimate a baseline fluorescent signal for each map by taking the mean of spatial bins with fluorescent signal below the 20th percentile. The ΔF/F of each spatial bin is then computed as follows:

where A is the mean fluorescent signal for a spatial bin. A pseudocount c is added when the baseline is below 10. For each spatial bin we obtained two vectors of population activity (one for each session). The length of the vector is equal to the total number of telencephalic PCs identified from either session. Correlation between the two activity vectors yields the PV correlation for a given spatial bin.

To determine the similarity of spatial activity maps we computed the correlation between spatial activity maps (that is, PF correlation or spatial correlation). Correlation was performed on spatial bins that are shared across both maps and normalized by the mean and variance of each map. All telencephalic cells identified as PCs in either session were used.

To measure the extent of PF shift across sessions, for each neuron we identified the COM of its PF in each session. We define PF shift as the distance between the COM of the cell’s PF in S1 and S2. Only cells with confined PFs (firing field size less than 30% of chamber size; section ‘Defining place fields’) in both sessions are included for this analysis.

For the within-session control we generate two separate spatial activity maps corresponding to the early and late halves of S1. PV correlation, PF correlation and PF shift are computed from the within-session control spatial activity maps using the procedure described above. For comparison with control we ensure that the same set of neurons (for PV correlation, PF correlation and PF shift) and spatial bins (for PV correlation and PF correlation) are used. One-sided Wilcoxon signed-rank tests are used to measure whether PF correlation and PV correlation are significantly lower than control, and whether PF shift is significantly higher than control.

Blurring of the spatial activity map

Blurring is the broadening of a PF at a given point on its boundary in the radially outward direction. For estimation of this blurring effect of PFs due to the speed of the fish, combined with calcium indicator dynamics, we compute an upper and a lower bound. The lower bound is computed by assuming a 10 Hz firing rate and a speed of the mean minus standard deviation; the upper bound assumes a firing rate of 100 Hz with a speed of the mean plus standard deviation. Speed distribution consists of pooled speed data from seven fish (Extended Data Fig. 1f). The data for the half-decay times for different firing rates are taken from ref. ⁵⁴. The half-time of temporal fluorescence decay is multiplied by the speed value to obtain the half-distance for spatial fluorescence decay (Extended Data Fig. 1g). Of this exponential spatial decay, the distance needed for a decay down to 80% of starting value is computed (Extended Data Fig. 1h); this matches our definition of PF and is used as a blurring estimate. Based on the behavioural data (Extended Data Fig. 1f) and calcium indicator kinetics, which both depend on firing rate⁵⁴, we estimate the radius of the PFs to be spatially blurred by 0.17–1.31 mm.

Isomap and quantification

Isomap³⁷ embedding was performed using Scikit-learn⁵⁵ with ‘n_neighbors = 100’. A rectangular matrix representing the population activity of all telencephalic PCs in a span of 30 min was constructed, an Isomap manifold was fit to the data (with each point in the manifold representing the population activity at one time point) and finally a two-dimensional embedding was extracted for visualization in Fig. 3a and computation in Fig. 3b. Because the implementation does not handle missing data, we filled in missing values in the activity trace for individual cells with the nearest preceding available value. In the case of missing values at the beginning of the experiment, a backwards filling is applied. For Fig. 3a,b the early (0–30 min) and late (60–90 min) windows of population activity data were fit separately and therefore have different two-dimensional embeddings. For Supplementary Video 2 we fit an Isomap manifold to the final 30 min of imaging S1 (before chamber rotation; Fig. 4m) to establish stable axes for two-dimensional embedding, and then repeatedly transformed each window of 30 min of population activity data into this embedding. Standard exclusion criteria based on movement were applied (spatial activity map in ‘Identification of PCs’).

To quantify the relationship between the two-dimensional manifold and the physical position of the fish we use neighbour distance, which quantifies the degree to which local neighbours in the manifold space are also local neighbours in the physical space of the chamber. In a given 30 min time window we analyse each time point in the two-dimensional manifold space (the ‘seed point’) by selecting its 30 nearest neighbours in the manifold space, then measuring the physical distance in the chamber between those 30 points and the seed point and averaging to obtain the mean physical neighbour distance of the seed point. We then compute the overall average physical neighbour distance by averaging this across all time points in the manifold. As a baseline, for each seed point, 30 random neighbours in the manifold are chosen and then physical neighbour distance is computed as before.

For analyses comparing between two sessions, or between the early and late intervals of a session (Fig. 3), the occupancy of each spatial bin was equalized by subsampling. That is, for each spatial bin, we identified the session or time interval having a lesser number of time points and randomly subsampled from the session or time window with more time points, so that both time windows had the same number of time points in each spatial bin.

Direct basis decoder

The direct basis decoder³⁶ is a linear decoder with no free parameters that predicts the animal’s position at each individual time point by a linear combination of the spatial activity maps, weighted with the activity of the corresponding place-encoding cell. All decoding and map construction was performed only at those time points at which the fish was moving (fish speed greater than 0.1 mm s^−1). Even though no parameters had to be learned, it is still necessary to compute the spatial activity map of each cell. To avoid circularity between computing the spatial activity map and testing the decoder we used a cross-validation scheme in which the neural data were divided into non-overlapping 1 min chunks. To test the decoder on each 1 min chunk we first computed the spatial activity map without including the test chunk or its two neighbouring chunks. The predictions of all 1 min chunks were concatenated as the prediction of the whole dataset. Decoder error was then computed as the mean distance between the predicted and actual position of the fish across the dataset.

Spatial activity maps were constructed as described above using spatial bins (side length 1.2 mm) and boundary-constrained Gaussian smoothing. Apart from the analysis shown in Extended Data Fig. 5c, the activity used in this map construction is time shifted by 2 s relative to the location of the fish, to counteract potential calcium lag dynamics. All maps were standardized by mean and standard deviation. To prepare the decoder, a 7.5 s boxcar average filter was applied to the activity and then maps of the most active 30% of cells were weighted by their respective activity and summed to form the decoder map. This nonlinear thresholding step was designed to omit low-intensity signals that would contribute noise to the decoding. The decoder map was then normalized for density differences in representation. To this end we calculated a representation histogram across all spatial bins, defined for each spatial bin as the number of PCs containing that bin in their primary PF (Defining place fields). Because we found that the effect of representation density on decoding error was sublinear, we normalized the decoder map by the third root of the representation histogram. The position estimate for each time point was then calculated by the COM of the 99th percentile of the decoder map. If not specified differently, 1,000 telencephalic cells of the highest spatial tuning per animal were used for all decoding analyses. For selection of the top spatially tuned cells we ranked each telencephalic place-encoding cell according to its specificity z-score and also according to its population specificity z-score, and then assigned its final rank according to the worse of the two ranks (Fig. 2f). This allows for a fair comparison between fish that may have varying numbers of PCs (Fig. 1g). For selection of the minimum number of cells needed for good decoding, an iterative, greedy algorithm was used (Fig. 2g). Starting with zero neurons, we find the single best neuron to add to the decoding set to minimize the resulting decoder error and then iteratively repeat this same greedy selection procedure to grow the decoding set, one neuron at a time.

For the analysis of decoder error by brain region (Fig. 2e), the 1,000 top spatially tuned cells were chosen for each defined region (whole brain, telencephalon, mes- and rhombencephalon). The random cell population was randomly selected from cells with a population z-score less than 1, to explicitly contain no PCs. We defined two baselines for evaluation of the decoder performance. For the uniform random baseline we measured the average decoder error of a decoder that outputs random positions sampled uniformly from the chamber. This procedure was repeated 1,000 times, with the mean decoder error taken as the uniform random baseline. For the behaviour-informed baseline we measured the average decoder error of a decoder that outputs the COM of fish positions in the chamber.

For all analyses, if not specified differently, only the final 75 min of each experiment were used for decoding. In the analysis of the decoder error as a function of number of cells included (Fig. 2f), the threshold for spatial tuning was gradually lowered until 10,000 cells were obtained (n = 7 fish). The two fish with fewer than 10,000 recorded cells in the telencephalon were hence excluded from this analysis. To avoid circularity, for Fig. 3d the shuffled specificity z-score and population z-score were calculated separately for the first and last 30 min of the experiments. Decoding for these two time windows was therefore based on the respective top-ranked PCs within each window.

We find that the non-redundant decoder starts to outperform the decoder using all cells from 17 cells onwards. The worse performance of the decoder using all cells is a consequence of the simple linear decoder design, which values the information of all cells equally; hence, less specific neurons can influence the decoder and slightly worsen the results. The advantages of this decoder, however, are the limited assumptions of the model, easy interpretability and impossibility of overfitting.

Regression and prediction of neural activity

We used ordinary least-squares regression to measure how much of the variance in place-encoding cell activity can be explained by different behavioural variables, including physical location, heading and speed. This is a much simpler model compared with previous work using a generalized linear model⁵⁶. The behaviour variables were discretized into bins, and an indicator function for each bin was added as a regressor in the model. The regression model can be summarized by the following formula:

where \({\lambda }_{n}\left(t\right)\) is the baseline-corrected neural activity for cell n at time t, \({\mu }_{n}\) represents baseline activity, \({w}_{i,n}^{(x)}{x}_{i,t}\) represents the contribution from the physical location of the fish, \({x}_{i,t}\) is the activity for spatial bin i at time t, L is the number of spatial bins (15 × 8 = 120), \({w}_{j,n}^{\left(h\right)}{h}_{j,t}\) represents the contribution from the heading of the fish, \({h}_{j,t}\) is the activity for heading bin j at time t, H is the number of heading bins (24), \({w}_{k,n}^{(s)}{s}_{k,t}\) represents the contribution from the speed of the fish, \({s}_{k,t}\) is the activity for speed bin k at time t and S = 24 is the number of speed bins. For comparison of contributions from spatial location, heading and speed, both individually and together, we tested ordinary least-squares regression in four cases: \({\lambda }_{n}(t)={\mu }_{n}+{\sum }_{i=1}^{L}{w}_{i,n}^{(x)}{x}_{i,t}\) (that is, with only spatial indicator functions), \({\lambda }_{n}(t)={\mu }_{n}+{\sum }_{j=1}^{H}{w}_{j,n}^{(h)}{h}_{j,t}\) (that is, with only heading indicator functions), \({\lambda }_{n}(t)={\mu }_{n}+{\sum }_{k=1}^{S}{w}_{k,n}^{(s)}{s}_{k,t}\) (that is, with only speed indicator functions) and, finally, the complete equation shown above. All models included a weak L2 regularization on the parameters with a penalty coefficient of 1^−10. For each regression model we report the resulting distribution of R² values across the telencephalic PCs shown in Extended Data Fig. 1b. Similarly, the distribution of R² values across other telencephalic cells is shown in Extended Data Fig. 1c. Standard exclusion criteria based on movement speed were applied (see spatial activity map in ‘Identification of PCs’).

Whole-brain PC maps

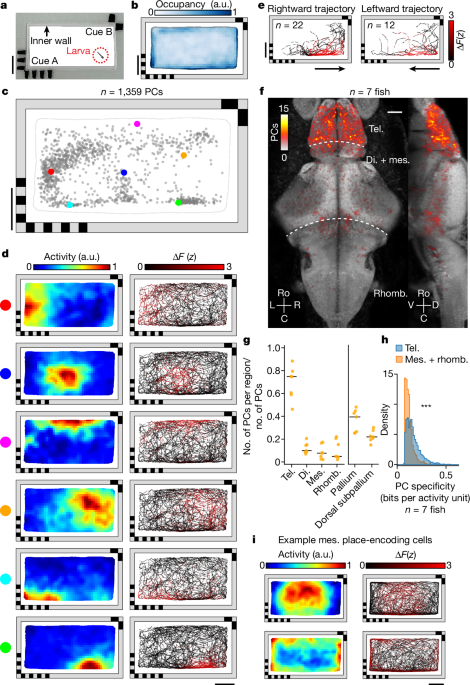
Following projection of the location of PCs from all fish to the same reference fish⁵², we accumulated all PCs into a three-dimensional histogram representing how many PCs were detected in each three-dimensional bin within the reference volume. We then convolved the three-dimensional histogram with a spherical convolution mask of radius 5 µm, such that each place-encoding cell contributes an increment of one count to all bins within a 5 µm radius. Maximum-intensity projections were then computed to visualize the anatomical distribution from multiple views (Fig. 1f).

BVC model

To search for cells whose firing properties follow the BVC model³⁴ we fitted a BVC model (see below) to candidate neurons in the telencephalon. The model predicts that the activity of these cells, f, integrates each boundary point (represented in polar coordinates r and θ relative to the animal) according to

where \(g(r,\theta )\) represents the firing rate relative to a preferred firing orientation ϕ and distance d from the boundary:

Here, \({\sigma }_{{\rm{rad}}}\) and \({\sigma }_{{\rm{ang}}}\) are the width of radial and angular tuning, respectively. Compared with the original model³⁴, which treats \({\sigma }_{{\rm{rad}}}\) as a variable that linearly depends on d, we treat \({\sigma }_{{\rm{rad}}}\) as a constant to be fit. A is a scaling factor and c is the baseline. Note that the bin size for spatial activity maps for this experiment is slightly smaller (side length 1.1 mm), to ensure sufficient resolution for accurate detection and representation of the inserted wall. When fitting the model to spatial activity maps, we first normalize the map by its standard deviation. During the fitting we constrain d to be between 0 and 10 bins (assuming BVCs fire close to the boundary), ϕ between −π and π, both \({\sigma }_{{\rm{rad}}}\) and \({\sigma }_{{\rm{ang}}}\) between 0 and 10, A between 0 and 100 and c between −10 and +10 activity units.

To test whether the activity of a given neuron is predicted by the BVC model we performed a three-session experiment—after a baseline session (45–95 min), an interior wall was introduced for S2 (45–95 min) and removed for S3 (45–95 min) (Extended Data Fig. 3b). We first identified all cells passing a minimum specificity criterion (over 0.01 bits per activity unit for all three sessions). Given the orientation of the inserted wall, only cells with PFs parallel to the inserted wall (from −45 to 45° or 135 to 225° in both S1 and S3) are suitable candidates for BVC analyses. We then fit the BVC model to the spatial activity maps of these candidate cells in S1 and then used the fitted model to generate predicted activity maps across sessions (with or without wall insertion).

We computed the Pearson correlation coefficient between the observed spatial activity map of each session with the predicted activity map generated by the fitted model. To test the significance of the Pearson correlation coefficient we circularly permuted the observed spatial activity maps approximately 1,100 times (same as the number of bins in the map) and recalculated the Pearson correlation coefficient for each permutation to construct the null distribution for a one-sided shuffle test.

Crucially, the BVC model predicts a duplication of PFs in S2. This duplicated firing field is expected to be absent in S1 and S3, which are predicted to have the same spatial activity map. Thus, to be classified as a BVC, a cell has to be consistent with the BVC model in all three sessions:

1. 1.

   For S1, Pearson correlation between the observed spatial activity map and model-predicted activity should be significantly higher relative to shuffle (P < 0.05, one-sided shuffle test as described above).

2. 2.

   For S2, Pearson correlation between the observed spatial activity map and model-predicted activity should be significantly higher relative to shuffle (P < 0.05, one-sided shuffle test) and the observed spatial activity map should have higher Pearson correlation with model-predicted activity with wall insertion than model-predicted activity without wall insertion.

3. 3.

   For S3, the spatial activity map should return to the map observed in S1 (PF correlation between S1 and S3 should be significantly higher relative to shuffle; P < 0.05, one-sided shuffle test).

Neighbourhood analysis

To quantify the degree to which potential clustering of PFs is maintained across sessions, we performed a neighbourhood analysis for each neuron (Fig. 6e). First, for each neuron we ranked all other neurons by their PF correlation to the neuron of interest in S1. We define neurons with the highest PF correlation as neighbours, with a systematically varied inclusion threshold from top 2% to top 100%. We define neighbour retention % as the number of neurons that remain neighbours in S2 divided by the number of original neighbours in S1. The mean neighbour retention % across all telencephalic PCs from either session is then plotted. This analysis is also carried out separately for cells whose PF is close to the edge (nearest distance of COM to edge 3 mm or less) and for cells whose firing field is away from the edge (nearest distance to edge greater than 3 mm). To avoid any potential contribution from imperfect cell merging we restricted this analysis to pairs of cells with a minimum anatomical distance of over 20 µm. A one-sided Wilcoxon signed-rank test was used to quantify whether neighbour retention % in the experiment was significantly worse than a within-session positive control (comparison between the early and late periods of S1). As a negative control we shuffled the cell indices in the second session 1,000 times to randomize relationships between neurons. Post shuffle, we calculated mean neighbour retention % across all telencephalic PCs from either session to generate a null distribution (that is, a shuffle control). A P value is calculated by counting the percentage of shuffles in which the mean neighbour retention % is higher than the shuffle control. For these significance tests we fixed the number of top correlated neighbours to 10%.

Significance tests for sample comparison

Wilcoxon signed-rank tests were used for paired location comparisons with equal sample size. Mann–Whitney U-tests were used for unpaired location comparison.

Animal care and transgenic lines

Experiments were carried out in accordance with the Animal Welfare Office at the University of Tübingen and the Regierungspräsidium. All experiments in rectangular chambers, and ABA experiments, used Tg(elavl3:H2B-GCaMP6s^+/+) with nacre (mitfa^{−/−}) at 6–9 days postfertilization. The remainder of the experiments used Tg(elavl3:H2B-GCaMP8s^+/+ or GCaMP8s^+/−) with nacre (mitfa^{−/−}) at 6–13 days postfertilization. In three of the rectangle-to-circle experiments the fish expressed an additional allele of Tg(elavl3:GCaMP6s). Fish were reared on a 14/10 h light/dark cycle at 25 °C. They were maintained in sets of 30 in E3 water and fed dry food daily.

Computer hardware for data acquisition and analysis

The tracking microscope was controlled by a rack-mounted, 12-core workstation with a Geforce RTX 3080 Ti graphics processing unit. Offline data analysis was performed using eight rack-mounted, 8- to 16-core Linux servers with four graphics processing units each (Geforce RTX 3080 Ti, RTX 2080 Ti or GTX 1080 Ti), or at the Max Planck Computing and Data Facility (Raven, A100-SXM4).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.