A neutral-atom Hubbard quantum simulator in the cryogenic regime

Lattice potential

In this work, the lattice potential is formed by three retro-reflected laser beams. Two beams are overlapped and mode-matched, propagating in the x-direction, and are referred to as the X and \(\barX\) beams, respectively. The third beam is propagating along the y-direction, orthogonal to the other two, and is referred to as the Y beam. As described in previous works^12,57, the X and Y beams are phase stabilized to form an interfering lattice. The frequency of the \(\barX\) beam is detuned by about 1.6 GHz from X and Y (Extended Data Fig. 1d,e). The frequency offset is converted to a lattice phase shift of π upon reflection from the retro-reflecting mirror, shifting the \(\barX\) lattice by half a site relative to the X lattice. This allows the \(\barX+Y\) lattice to split each unit cell in the X + Y lattice symmetrically into two sites. All three beams are reflected from a super-polished substrate in the z-direction at an angle of θ = 69.2(1)° before being retro-reflected¹², which forms a three-dimensional lattice potential. The lattice potential in the z-direction provides confinement with a trapping frequency much larger than all relevant energy scales in the xy plane lattices, and the tunnelling along the z-direction is negligible during the experimental sequences. This allows for a near-ideal realization of a 2D system in the xy plane after the atoms are selectively loaded into a single layer of the z lattice. The potential of the 2D lattice can be written as

Here, \(\barr=8.27(1) \% \) denotes the Fresnel loss present at the surface of the glass cell, k_x = k_y = 2π sin θ/λ are the lattice vectors in the xy plane, and λ = 1,064 nm. Owing to loss, the four interference terms cannot be combined except when the interference time phase ϕ between X and Y is 0 or π. Note that the lattice depths \(V_x,\barx,y\) do not directly correspond to the lattice depths in an ideal retro-reflected square lattice, because of the finite incident angle in the z-direction and losses due to the presence of the glass cell.

Experimental methods

As in previous work¹², we prepare an ultracold, spin-balanced Fermi gas of ⁶Li atoms in the lowest two hyperfine states by evaporative cooling in a crossed optical dipole trap. Spin balance is achieved through a microwave mixing process⁵⁸ with a duration of 300 ms, ensuring the SU(2) symmetry of the Fermi gas. The ultracold ⁶Li atoms are then loaded from the optical dipole trap into the interfering (long-spacing) lattice. The interfering lattice is a square lattice with √2 larger spacing than the non-interfering (short-spacing) lattice and is formed by the actively phase-stabilized X and Y beams¹² using equal intensity. This initial lattice loading is performed in 100 ms, and the final lattice depths after loading are V_X = V_Y = 2.88(1)E_R. Here, E_R = h²/(8ma²) = 25.49(4) kHz denotes the recoil energy and a denotes the lattice spacing. We set the magnetic field to 550 G, resulting in an s-wave scattering length of a_s ≃ 84a₀, and ensure that the applied field settles before lattice loading. At the start of lattice loading, we turn on a blue-detuned confining potential formed by one of two DMDs, which we refer to as DMD0 and DMD1. DMD0 is turned on for 60 ms (see section ‘Characterization of BI’) and, together with the harmonic confinement provided by the lattice, controls the density profile of the atoms. This redistributes the entropy in the system, creating a BI that is in thermal contact with a dilute metallic reservoir (see section ‘Characterization of BI’). Once the loading is complete, we turn on a second blue-detuned DMD potential projected using DMD1 in 5 ms (ref. ³¹), which acts as a wall to separate the BI from the reservoir in subsequent steps in the experiment.

Experimental sequence for the half-filling data

As described in ref. ¹⁵, the phase transition from a BI to a half-filled Mott insulator with long-range antiferromagnetic correlations can be tuned by adjusting the ratio between inter- and intra-dimer tunnelling amplitudes. In the Hubbard model, the intra-dimer tunnelling t_d is proportional to the band gap Δ_g in the BI limit. The large band gap of Δ_g ≃ 100 kHz allows for a fast ramp of the \(\barX\) and Y beams in 2 ms, while remaining adiabatic relative to motional energy scales. The final Y and \(\barX\) lattice depths are 9.29(3)E_R and 6.28(2)E_R, respectively. These values satisfy the relation \(V_X+V_\barX\approx V_Y\), ensuring that the harmonic confinement induced by the Gaussian intensity profile of the lattice beams is approximately rotationally symmetric. Next, we ramp the depth of X to 0.19(1)E_R in 15 ms, and simultaneously increase the depth of \(\barX\) to 9.06(3)E_R. This compensates for the decrease of V_X, and maintains \(V_X+V_\barX\approx V_Y\). During this ramp, each site in the long-spacing lattice is split into a dimer, as shown in Extended Data Fig. 1d. In quasimomentum space, this corresponds to reducing the band gap Δ_g between the ground band and the first excited band, while keeping the gaps from the ground band to higher bands nearly unchanged. The ramp needs to be slower than the band gap Δ_g between the ground and first excited bands to be adiabatic. This gap decreases with decreasing X lattice depth. We separate the ramp into two segments with a duration of 3 ms before and 10 ms after depths of \(V_X=0.52(1)E_\rmR,V_\barX=8.74(3)E_\rmR\). The slower ramp at lower X depths helps to accommodate the requirement of adiabaticity.

The set point of V_X is further reduced to 0.032E_R, and \(V_\barX\) increased to its final value of 9.22(3)E_R. Note that there is a systematic uncertainty in V_X below 0.1E_R because of residual leakage from the retro-reflected \(\barX\) lattice onto the X lattice intensity regulation photodiode. This causes an offset as large as 0.01E_R and decreases the actual X lattice depth. During the above ramp, the phase transition from spin singlets to antiferromagnetic order is expected to occur. The ramp speed is 50 ms, which is a balance between adiabaticity and heating from the optical lattice. Despite the presence of long-range antiferromagnetic correlations, the resulting state still exhibits dimerized spin correlations due to the imbalanced inter- and intra-dimer tunnelling along the x-direction (see section ‘Calibration of tunnelling and lattice parameters’). We further decrease the set point of the X lattice over 30 ms to 0.016E_R, which is the lowest depth that allows us to maintain phase stabilization between the X and Y lattices. The depth of V_X = 0.016E_R is not sufficient to remove the dimerization of the tunnelling, and so we further ramp the setpoint of the phase stabilization from ϕ = 0 to π/2. Note that the contribution from phase noise to intensity noise is negligible at these low values of V_X. Although this step is supposed to eliminate the interference lattice⁵⁹, loss in the retro-reflected lattice beam (see section ‘Lattice potential’) results in imperfect suppression of the interference term⁶⁰, and thus a potential offset between the A and B sublattices of the square lattice. We use numerical simulations to confirm that this sublattice offset does not alter the relevant physics at half-filling (see section ‘Lattice potential calibration’).

To carry out the experiments shown in Fig. 4 (see section ‘Experimental sequence for doped data’) on the doped Hubbard model, we upgraded the apparatus with a non-reciprocal attenuator (see section ‘Non-reciprocal attenuator’). This allows us to decrease V_X to a depth of 3.2(3) × 10⁻⁵E_R, corresponding to negligible tunnelling dimerization. With this upgrade, we can avoid ramping the phase stabilization setpoint ϕ and simply trigger the attenuator at the beginning of the dimerized lattice ramp. As a verification, we repeat the experiments at half-filling with the attenuator while keeping ϕ = 0. Under these conditions, we obtain a temperature of T/t ≃ 0.1, as shown in Extended Data Fig. 2. These measurements were performed without careful optimization and obtained over a 12-h period without realignment. The achieved temperature is consistent with those obtained without the attenuator for similar data taking durations without realignment. We therefore attribute the slight increase in temperature compared to the data shown in Fig. 3 to lattice drifts (see section ‘Effects of alignment’).

In the short-spacing square lattice, the harmonic confinement imposed by the Gaussian intensity envelope is not compensated. As a result, the final density profile is not flat except in a radius r = 5 region near the lattice centre at half-filling. If all of the atoms in the initial BI are kept inside the DMD0 confining potential, the harmonic confinement will increase the chemical potential μ. According to DQMC simulations at the Hubbard interaction studied in most parts of this work of U/t ≃ 8, |μ| > t will lead to non-negligible doping δ > 1%. Therefore, harmonic confinement may introduce particle dopants into the system. If the DMD0 potential had arbitrarily fine spatial resolution, allowing for an infinitely sharp wall, then as long as the DMD0 potential V_D remains smaller than the band gap and V_D ≫ U, the system would have a well-defined open boundary. However, the resolution of the DMD0 potential is limited by the numerical aperture (NA = 0.7) of the microscope objective, and the wavelength of 650 nm used to create the DMD potentials. The excess atoms residing on the finite slope of the DMD0 potential will further increase the chemical potential μ of the central system as a function of the strength of the DMD0 potential, causing additional particle doping. This doping leads to charge transport through the system at strong Hubbard interaction, which we suspect leads to substantial heating. To minimize charge transport and heating, as described in the main text, the potential strength of DMD0 is scanned and optimized for each ramp. We find the lowest temperatures are realized when the DMD0 potential is set to maintain μ ≃ 0 in the lattice centre, such that no transport occurs at this location throughout the entire ramp. Close to the boundary of the DMD0 potential, the decreased local chemical potential causes excess atoms to flow out of the central region and form a secondary reservoir. This could be beneficial for reducing the final temperature by realizing a secondary entropy redistribution step. We start to ramp the magnetic field to its final value of 620 G after the dimerized lattice has mostly been formed, and where the density distribution matches that of the short-spacing square lattice. We find this is important to reach low temperatures, which we ascribe to interaction-induced heating in transport at large U/t and to interaction-driven changes in the density profile.

The tunnelling amplitudes for all datasets are summarized in Extended Data Table 1. Once the lattice and DMD0 ramp finishes, we immediately quench the lattice potential to \(V_\barX,Y > 60E_\rmR\) within 50 μs to freeze the dynamics before imaging. We confirmed that this quench is faster than doublon–hole dynamics and slower than band excitations. The probed singlon density starts to increase once the quench time is slower than 100 μs because of the combination of virtual doublon–hole excitations and starts to decrease once the quench time is faster than 20 μs because of excitation to higher bands.

Experimental sequence for doped data

The transport described in section ‘Experimental sequence for the half-filling data’ is necessary only because of imperfections of the potential, including finite optical resolution and harmonic confinement. Splitting a BI in the long-spacing lattice naturally gives a half-filled state in the short-spacing lattice with μ ≃ 0. To reach a final state with finite doping, coherent redistribution of atom density across the entire system is required, which poses more challenges to suppress heating during atom transport.

After isolating the BI, we first reduce the lattice depth to V_X = V_Y = 0.50(1)E_R in 30 ms, which increases the kinetic energy scale and further reduces the interaction strength before splitting into a Fermi liquid. This depth corresponds to around 20% of the original lattice depth and is chosen to maximize the tunnelling energy in the lowest band to enhance adiabaticity and reduce lattice-induced heating, while still maintaining a bandwidth smaller than the height of the DMD0 potential. The latter constraint is important because otherwise the atoms would have enough kinetic energy to move out of the confining potential, leading to uncontrolled transport. Another heuristic intuition is to maintain a finite band gap such that the Fermi surface before and after splitting are approximately matched. In the non-interacting limit, the quasimomenta of the atoms are conserved in a homogeneous lattice, and deformation of the occupation in quasimomentum space leads to diabatic transfer of atoms to excited states. In an ideal tight-binding model with only nearest-neighbour tunnelling, the full first Brillouin zone of the long-spacing lattice matches the Fermi surface of the half-filled first Brillouin zone of the short-spacing lattice (Fig. 4c). The approximate match between the occupied states before and after splitting may minimize the deformation of the Fermi surface, and therefore the heating process above. A finite band gap also suppresses diabatic excitation into higher bands. The reduced lattice depths before splitting weaken the confinement in the z-direction, potentially leading to tunnelling in the z-direction. To avoid this, we turn on a vertical lattice to allow the system to always be treated as 2D.

Unlike at half-filling, where the Mott insulating state is robust against potential variations, doped Hubbard systems are compressible and sensitive to potential offsets. We, therefore, upgraded the lattices with a non-reciprocal attenuator that allows us to almost completely turn off the X lattice, while maintaining phase stabilization between the X and Y lattices at ϕ = 0 (see section ‘Non-reciprocal attenuator’). An interference phase setpoint of ϕ = 0 ensures no potential offset, and therefore no density offset between the A and B sublattices. We ramp on \(\barX\) to 0.50(1)E_R, and ramp X to 3.2(3) × 10⁻⁵E_R in 30 ms. Owing to its low value, the X depth is directly calibrated using a power meter (PM100D and S121C from Thorlabs). We trigger the attenuator at the beginning of this ramp to maintain phase stabilization while ramping X. At the end of this ramp, the lattice has negligible tunnelling dimerization. At this stage, the splitting sequence is complete, and the first Brillouin zone doubled.

Expansion of the atom cloud is achieved by lowering the DMD0 potential in 50 ms, accompanied by a ramp of the magnetic field from 550 G to 590 G. This expansion time is chosen to allow the magnetic field to settle. Decreasing the DMD0 potential allows atoms to flow out of the confining potential, forming a dilute secondary reservoir confined by the DMD1 wall. The DMD0 potential is chosen to adjust the central density to the desired value in the final state, which will minimize transport during lattice reloading. As expansion corresponds to a reduction of the Fermi momentum, a change in quasimomenta is necessary. As a result, it is possible that increased scattering lengths due to the higher magnetic field may facilitate thermalization during expansion.

The prepared state is a weakly interacting Fermi gas in equilibrium, which is similar to the state used to load the lattice in previous works¹¹, but at a much lower temperature. We then load the non-interfering lattice by ramping the \(\barX\) and Y lattice depths up to \(V_\barX=11.0(1)E_R,\)\(V_Y=11.0(1)E_R\). Here, the lattice depths are deeper than in the half-filling protocol to allow us to reach an interaction strength of U/t ≃ 8 at a lower magnetic field of 590 G (see section ‘Choice of lattice depths and magnetic field’) to maintain the atom density profile, and minimize transport in the regime in which U/t is large, we lower the DMD0 potential and the DMD1 wall to accommodate reduced tunnelling energies at higher lattice depths during the above ramp. After lattice reloading, we freeze the dynamics within 50 μs before imaging.

Potentials of DMD0

We use an incoherent light source at 650 nm to illuminate the DMDs, which is blue detuned of the D1 and D2 transitions in Li, and forms a repulsive potential. For experiments at half-filling, the volcano-shaped potential created by DMD0 is composed of a paraboloid, which is chosen to compensate the harmonic confinement imposed by the lattice beams^11,31, and a circular central cutout region that we will refer to as the crater (Extended Data Fig. 1). The transition from the paraboloid to the crater is sharp (within 1 pixel) on DMD0, which induces diffraction fringes on the potential due to the finite resolution of the imaging system.

To allow expansion for doped systems, we create the flattened volcano-shaped potential (see section ‘Adiabaticity of expansion after splitting’) by applying a cutoff on the maximum amplitude of the volcano potential (Extended Data Fig. 1g). This forms a flat ring-shaped region surrounding the crater. As described in section ‘Characterization of BI’, the flattened volcano-shaped potential may result in worse BI fidelity than without flattening. We choose to work with the largest flattened region for which we do not detect a reduction in BI fidelity.

Non-reciprocal attenuator

As described in section ‘Experimental sequence for doped data’, even when ϕ = 0, the intensity of the X lattice needs to be reduced by more than that in the half-filled case to avoid sublattice offsets. This is challenging because of the reciprocal nature of most optical attenuators, including acousto-optical modulators or ND filters, which act on the beam both in the forward direction (towards the atoms) and in the reverse direction (on retro-reflection, returning to the detection photodiode). A 50-dB attenuation of the X lattice beam, therefore, leads to a 100-dB attenuation of the laser intensity on the phase stabilization photodiode, resulting in greatly decreased gain and signal-to-noise ratio, making it impossible to perform effective stabilization. We solve this problem by introducing a non-reciprocal attenuator⁶⁰, which applies variable and differing levels of attenuation to the forward and reverse beams. This allows us to reduce the X lattice depth by five orders of magnitude, while keeping the interference phase actively stabilized. Under these conditions, we detect no tunnelling dimerization or potential offset (see section ‘Experimental verification’).

Effects of alignment

We find that the main source of instability in the experiment is the drift of the lattice positions (especially of the \(\barX\) lattice relative to the X lattice). This results in drifts in the lattice harmonic confinement and corresponding shifts in the position of the peak atom density in the cloud. The lattice position is affected by temperature and humidity fluctuations in the lab and remains stable for about 0.5 h, which is the typical duration of a contiguous scan. We observe drifts in lattice position on longer timescales, which may lead to heating due to excess transport during the lattice ramps. Empirically, we find the strongest effects of heating due to lattice drifts at half-filling.

For the doped data presented in Fig. 4, we average over ROIs at the centre of the trap with different radii, in which the effects of harmonic confinement are minimized. However, the lattice drifts shift the atom distribution relative to the DMD0 potential, which introduces a potential gradient within the ROI. Therefore, for data presented in Figs. 3 and 4, we re-centre the lattice beam positions about every 1 h by maximizing the light back-coupled into the lattice optical fibres.

The drifts of the DMD potentials along the x- and y-directions are strongly suppressed by the magnification of the high NA objective used to project them. We find that focus drifts along the z-direction occur over the course of weeks, which is convenient to correct.

Choice of lattice depths and magnetic field

The Hamiltonian of ultracold fermionic atoms moving and interacting in optical lattices naturally realizes the Hubbard model, with corrections in the form of beyond-nearest-neighbour tunnelling, density-assisted tunnelling, off-site interactions and higher bands effects⁶¹. Shallow lattices are preferred from an experimental perspective because, at a fixed target value of U/t, larger tunnelling energies make all energy scales higher. Harmonic confinement is reduced in shallower lattices too, which, combined with the increased tunnelling energies, results in a more homogeneous density distribution. However, once the lattices are too shallow, longer-range tunnelling grows appreciably, and the band gap decreases. These effects lead to deviations from the Hubbard Hamiltonian and a breakdown of the tight-binding and single-band approximation. As lattice depth increases the band gap increases, the Wannier function are more localized, a smaller scattering length a_s is needed to achieve the same value of U/t, and the above corrections are exponentially suppressed compared with nearest-neighbour tunnelling t and on-site interaction U. Deep lattices are, therefore, preferred from a theoretical perspective, and a tradeoff between experimental performance and asymptotic realization of the Hubbard model in an exact manner needs to be made. In the non-interfering (short-spacing) lattice, in the half-filled case with \(V_\barX=9.22(3)E_\rmR,V_Y=9.29(3)E_\rmR\), which yields a radial band gap of Δ_xy,g ≃ 83 kHz and a vertical band gap Δ_z,g ≃ 42 kHz, we find the next-nearest-neighbour d = (2, 0), (0, 2) tunnelling to be t″ ≃ 0.042t. In the doped case with \(V_\barX=V_Y=11.0(1)E_\rmR\), which yields a radial band gap of Δ_xy,g ≃ 93 kHz and a vertical band gap Δ_z,g ≃ 47 kHz, we find the next-nearest-neighbour tunnelling to be t″ ≃ 0.029t. Note that the radial lattice is nearly separable in the x– and y-directions, resulting in vanishing tunnelling along directions other than x or y. Therefore, for the experimental parameters in this work, the single-band, 2D and tight-binding approximations are well satisfied. Note that the lattice depths provided here take Fresnel loss and the angle of polarization in the apparatus into account. The quoted depths are, therefore, higher than those of an idealized retro-reflected square lattice with the same band properties.

In practice, we find that the maximum s-wave scattering length a_s available to achieve the targeted Hubbard parameter U/t sets the limit on the magnitude of tunnelling amplitudes. This is because shallower lattices yield larger tunnellings and smaller integrals of the Wannier functions, which requires increased a_s to achieve a targeted U/t. In the vicinity of the Feshbach resonance, the universal scaling of the fermion three-body recombination rate is \(\kappa \propto a_\rms^6\) (ref. ⁶²). Increasing the s-wave scattering length will eventually lead to excessive three-body loss and thus heating. We find that if the atoms are kept in a lattice with a depth of about 10E_R, as applies to the half-filling data, a_s = 512a₀ at 620 G is the highest scattering length that does not lead to noticeable excess heating. To achieve U/t = 8, we set the lattice depths to 9.2E_R. To obtain the doped data, the lattices are ramped down to 0.5E_R for expansion. Here, the lack of protection against three-body recombination from the lattice leads to significant heating at 620 G magnetic field. We, therefore, choose to work at a_s = 294.5a₀ at 590 G and set the final lattice depth after reloading to 11E_R. Details of the lattice parameters are listed in Extended Data Table 1.

Imaging procedure and fidelities

We perform site-resolved fluorescence imaging in the short-spacing square lattice as described in ref. ⁶³. The fidelity of correctly determining the occupation of a lattice site is F_i = 99.4(6)%.

Imaging in the long-spacing lattice differs from imaging in the short-spacing lattice and is described in ref. ¹². To image the BI with parity projection, we set the frequency detuning between \(\barX\) and X to 850 MHz using a radiofrequency synthesizer, which ensures good overlap with the X–Y and imaging lattices. This allows for deterministic atom transfer between the physics and imaging lattices, despite the fact that the imaging lattice contains twice as many sites as the physics lattice. As described in ref. ⁶⁰, doublons are converted into molecules by ramping through a narrow Feshbach resonance at 543 G and are subsequently lost because of light-assisted collisions. We report a combined imaging fidelity, including detection fidelity and physics-imaging transfer fidelity, of 99% (ref. ⁵⁷).

Imaging with full charge resolution in the long-spacing and dimer lattices is described in ref. ⁵⁷. The dimer lattice is adiabatically connected to the long-spacing lattice before the gap between the ground band and the first excited band closes. We set the frequency detuning of \(\barX\) relative to X to 1,552 MHz, which sets the position of the potential minimum of the \(\barX+Y\) lattice to be symmetric with respect to each unit cell in the long-spacing lattice formed by X + Y, and in the dimer lattice formed by \(X+\barX+Y\). Each site in the long-spacing and dimer lattice is symmetrically split into two, with a negligible potential offset between the two minima of \(\barX+Y\). Moreover, we ramp the magnetic field to 610 G to generate strong on-site interactions between the atoms on doubly occupied sites. This facilitates adiabatic transfer of doubly occupied sites in the long-spacing and dimer lattice to singly occupied sites in the \(\barX+Y\) lattice. We find the doublon detection fidelity to be 98% after image reconstruction.

Data analysis

In Figs. 2 (excluding Fig. 2b), 3 and 4, two-point spin correlation functions are spatially averaged over all pairs of sites within a circular ROI centred on the atomic cloud. Atomic density decreases away from the centre as a result of the confining potential imposed by the lattice beams and the DMDs. A large potential gradient would enhance the effective superexchange interaction J for a site-to-site potential offset of Δ_V < U and suppress magnetic interactions with a kinetic origin⁵⁷. We, therefore, chose an ROI radius of r = 6 sites in Fig. 2, r = 5 sites in Fig. 3, and r = 3, 4 and 5 sites in Fig. 4, to limit the potential variation. This limits the variation of the radially averaged singlon density to about 2% within the ROI. The correlation maps for r = 4 and 5 of the doped data are shown in Extended Data Fig. 3a,b. For large dopings, for which only short-range antiferromagnetic correlations are present, the sign-corrected, radially averaged spin correlations \((-)^C_d^zz\) may become negative at certain long bond distances. This could be induced by harmonic confinement or residual disorder of the lattice potentials and will be explored in future works.

In bipartite dimerized lattices (Fig. 2), we separately average the spin correlation function \(\langle S_\bfr^zS_\bfr+\bfd^z\rangle _\mathcalS\) over reference sites \(\bfr\in \mathcalS\) belonging to one of the two sublattices \(\mathcalS=\mathcalA,\mathcalB\) and for all bond vectors d. Assuming inversion symmetry, we obtain and plot the sublattice-averaged spin correlation function \(\langle S_\bfr^zS^z\bfr+\bfd\rangle =(\langle S_\bfr^zS_\bfr+\bfd^z\rangle _\mathcalA+\langle S_\bfr^zS_\bfr-\bfd^z\rangle _\mathcalB)/2\). All error bars indicate the 1σ confidence interval obtained using bootstrap sampling across all experimental snapshots of a given dataset with 500 randomly selected samples. The number of experimental realizations for each dataset is reported in Extended Data Table 1.

To convert the experimentally measured singlon density \(n_\rms,det\) to doping δ in Fig. 4, we first correct for imaging fidelity to extract \(n_\rms,\rmcorrected=n_\rms,\det /F_i\). We then use the doublon density n_d as a function of density n obtained from CP-AFQMC simulations at T/t = 0 to reconstruct the doublon density as a function of singlon density n_d(n_s) = n_d(n − 2n_d). Finally, we compute the density \(n_\exp =n_\rms,\rmcorrected\,+\) \(2n_\rmd(n_\rms,\rmcorrected)\) and doping \(\delta _\exp =1-n_\exp \) of the experimental data.

In Extended Data Fig. 4b, we plot the temperature dependence of the doublon density up to n = 0.85. Similar to half-filling, the temperature dependence is negligible compared with the statistical errors in our detected densities for T/t < 0.15. Although in these CP-AFQMC calculations, the n_d results are not as accurate at higher densities of n ∈ (0.85, 1), interpolating between n = 0.85 and half-filling suggests that the temperature dependence of the doublon density is still negligible for T/t < 0.15. This is supported by the fact that the energy scale associated with doublons is the interaction strength of U ≫ t ≫ T. Therefore, using the ground-state doublon density leads to negligible systematic errors in the reported quantities.

Discrepancy between experimentally measured spin correlations and CP-AFQMC results

To better understand the discrepancy between the experimental measurements of beyond-nearest-neighbour spin correlations in the presence of doping and CP-AFQMC simulations in Fig. 4, we explore a few possible sources of similar deviations.

As described in section ‘Calibration of Hubbard interaction U’, we calibrate U/t using the singlon density at half-filling, where n_s reaches its maximum. We also compare experimentally measured spin correlations as a function of the measured singlon density n_s to T = 0 data from CP-AFQMC. The singlon density is directly measured in the experiment and does not involve converting n_s to doping using numerical data. We confirmed that a miscalibration of U/t seems insufficient to explain the observed discrepancy. However, higher-order corrections to the experimental Hamiltonian, including density-dependent terms, may lead to systematic deviations at finite doping from the calibration performed at half-filling. A complete comparison between experimental and numerical data requires a comprehensive characterization of the experimental Hamiltonian and the development of calibration techniques that directly probe the doped regimes.

The constrained-path approximation used in the numerical simulations may also introduce systematic errors. To explore this possibility, we compare experimental and CP-AFQMC data at elevated temperatures with numerically exact DQMC simulations. When simulating the doped Hubbard model, the sign problem in DQMC leads to an exponential overhead with decreasing temperature. Given accessible computational resources, we first perform DQMC at T/t = 0.25 and U/t = 8 in an 8 × 8 system and compare the results to those obtained with CP-AFQMC with the same parameters but in a 12 × 12 system (Fig. 4). Both the DQMC and CP-AFQMC simulations use periodic boundary condition (PBC). For these DQMC simulations, we used the QUEST package⁶⁴ with a time step of δτ = 0.02, 5,000 thermalization sweeps and 200,000 measurement sweeps, which are repeated with random seeds for up to 4,000 runs for values of the density with severe sign problems. The experimental data are obtained with U/t = 8.2(2) and using the standard loading sequence (without engineering the DMD potential) in refs. ^12,63. The harmonic confinement due to the lattice intensity profile leads to a slow variation of the filling from the centre to the edge of the trap. We tune the atom number such that it reaches half-filling at the centre of a region of radius r = 6. This allows us to perform accurate thermometry of the entire atom cloud by comparing with numerically exact simulation results at half-filling without the need for numerical results in the doped regime. At larger distances from the trap centre of r > 6, the filling slowly decreases. Radially binning the data allows us to probe spin correlations as a function of varying singlon density and, therefore, doping at the calibrated temperatures.

We focus on the short-range spin correlations \(C_d^zz\) up to \(d=\sqrt5\) in Extended Data Fig. 5a,b. Given the short correlation lengths at this elevated temperature, and at finite doping, finite-size effects are expected to be negligible. At a density of n = 0.995 and chemical potential of μ/t = −1.0, in which the correlation lengths are expected to be longer than at larger doping, we find that the DQMC and CP-AFQMC simulations are in good agreement for all short-range correlations. Moreover, at T/t = 0.33, we confirm that there is no difference between DQMC simulations performed in 8 × 8 and 12 × 12 lattices.

We find that good agreement between experimental data, DQMC and CP-AFQMC on the nearest-neighbour correlation \(C_1^zz\) holds for all doping values at which we performed measurements or simulations. However, for a doping range of δ ∈ [5%, 10%] and bond distances \(d=\sqrt2,2,\sqrt5\), the results obtained from DQMC suggest stronger correlations, with which experimental data show good agreement (Extended Data Fig. 5a). This trend is consistent with the behaviour shown in Fig. 4. The large statistical error bars in the DQMC data make it difficult to draw a definitive conclusion, especially because the estimated errors are themselves unreliable because of the vanishing average signs.

At even higher temperatures of T/t = 0.33, the sign problem is less severe, and we can compare DQMC and CP-AFQMC in a 12 × 12 system. We find smaller, but qualitatively similar, discrepancies in which spin correlations \(C_\sqrt2^zz,C_2^zz\) computed from DQMC are stronger than CP-AFQMC for doping below 15% (Extended Data Fig. 5b). Owing to the reduced magnitude of the spin correlations, experimental data performed at this temperature seem to be statistically consistent with both numerical simulations. Future work should be able to address this by using a better trial density matrix or an improved form of the self-consistent constraint in CP-AFQMC and more systematic studies.

Lattice potential calibration

To measure the lattice trapping potential, we measure the density profile of a non-interacting spin-polarized Fermi gas loaded into the lattice, and, by taking the local density approximation, invert the non-interacting equation of state to obtain the local chemical potential. The spin-polarized Fermi gas is prepared by performing evaporative cooling with states 1 and 2 at 321 G, followed by a magnetic gradient-assisted spill-out of state 1 at 27 G, where state 2 is magnetically insensitive and therefore remains trapped. Pauli exclusion in a spin-polarized Fermi gas prevents double occupancy (and associated parity projection during imaging), meaning that the measured density can be mapped unambiguously to a particular value of the chemical potential. The uncertainty in the above calibration procedure is dominated by statistical errors and is not strongly dependent on the assumed temperature of the Fermi gas. We take a conservative estimate of T/t = 0.5 based on independent calibrations of the spin-polarized Fermi gas, but the results do not change significantly when assuming a temperature in the range T/t ∈ [0, 1].

Using the above procedure, the harmonic confinement of doped data (Fig. 4) is measured as V_H = 0.0152(6)t/(site)²r², where r denotes the radial distance measured in sites from the lattice centre.

The half-filled data at U/t = 8.3(2) (Fig. 3) was taken before the addition of the non-reciprocal attenuator; so an offset between the A and B sublattices is present. Using the procedure described above, we find that the difference in the mean local potential in the A and B sublattices is Δμ = 0.75(3)t. This is in good agreement with the expected offset of 0.8(4)t given the geometry of the lattice. The uncertainty in the expected offset is primarily because of uncertainty in the applied X lattice depth at very low values.

To investigate the effects of sublattice offsets on spin correlations, we perform DQMC simulations at T/t = 0.15, 0.3 on an 8 × 8 system and CP-AFQMC simulations at T/t = 0 on a 12 × 12 system. DQMC simulation at T/t ≥ 0.15 show that an offset as large as Δμ = 2t (defined as a symmetric sublattice offset about mean μ = 0) has little effect on spin correlations (Extended Data Fig. 4a). At T/t = 0, CP-AFQMC shows no effects on the spin correlations for Δμ = t and a small decrease in spin correlations for Δμ = 2t. This decrease is smaller than the statistical error in the experimental data; so we conclude that sublattice offsets are not a concern for the above dataset.

Characterization of BI

BI fidelity

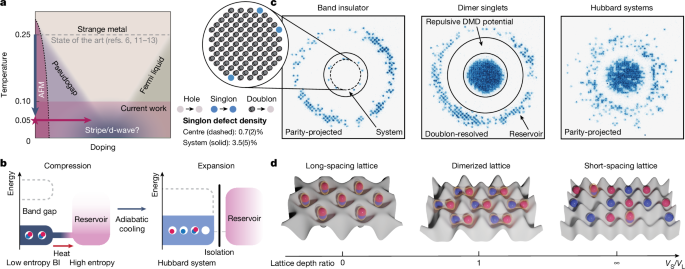
We characterize the fidelity of the BI using the singlon density F_BI = 1 − n_s, assuming that a perfect BI has a doublon on every site. We can image the BI state with parity projection in the long-spacing lattice, in which doublons are lost because of light-assisted collisions⁶³ (Fig. 1c, left). Alternatively, we can directly image the doublon population by splitting each long-spacing site into two after freezing the dynamics to reconstruct the population with full density resolution⁵⁷ (Fig. 1c, middle).

Using density-resolved imaging, we measure the doublon density to be n_d = 98.2(5)%, the singlon density to be n_s = 1.8(5)%, and the hole density n_h to be consistent with zero within a central ROI that does not include the boundary of the crater. The ROI covers a circular region with a radius of r = 6 sites in the long-spacing lattice (about r = 9 in the short-spacing lattice), which is one site (two sites) smaller than the radius of the crater. Note that given the fidelity of doublon detection in the experiment, the above numbers are consistent with a doublon fraction of unity. The total number of atoms detected in the crater is N_r=10 = 342(1).

The above measurements confirm that the empty sites appearing in the parity-projected images are doublons instead of holes. Given this observation, parity-projected imaging offers better sensitivity to the doublon population because it is immune to atom loss during fluorescence imaging. The remaining errors in parity-projected imaging of doublons include the fidelity of removing doublons through light-assisted collisions and atoms hopping to a different 2D layer during imaging. At present, we do not have an independent calibration of these errors; so the measurements of the BI fidelity below constitute a lower bound.

Using parity-projected imaging, we find that most of the singly occupied sites occur at the edge of the crater. We note that the crater is not aligned to the optical lattice in a site-resolved manner. When combined with the finite resolution of the imaging system, this results in imperfectly controlled local potentials on the sites falling along the edge of the crater. The equation of state on these sites may not favour doublons. Moreover, the local density approximation may not hold in the presence of this abrupt potential variation. We minimize the population of singlons on the edge by increasing the lattice depths and DMD0 potential strengths, such that the tunnelling energy t is small compared with the site-to-site potential difference at the crater edge. We also set the magnetic field at 550 G to lower the Hubbard interaction U, which prevents the formation of a wide Mott plateau. The detected singlon density is n_s,r=4 = 0.5(3)% in a central disk with r = 4, and n_s,r=6 = 0.7(2)% in a disk with r = 6. Including the edge, the singlon population in the crater is N_r=10 = 11.9(7). However, the presence of singlons on the edge obscures the estimation of entropy in the BI because these singlons are not necessarily excitations. By contrast, because the density of states along the crater edge can be finite, these singlons can host a significant amount of entropy. Taking this into account, we choose to define the BI fidelity F_BI = 1 − n_s,r=6 in the central region with r = 6 as a figure of merit to optimize the entropy redistribution procedure.

To optimize the initial loading of the BI, the DMD0 potential ramp is split into a linear ramp and a holding phase. Once the lattice depths are high and the tunnelling energy correspondingly small, the atoms may not redistribute for continued changes in the DMD0 potential (that is, the ramp is not adiabatic). We also limit the initial ramp rate to avoid creating band excitations in shallow lattices.

The volcano-shaped DMD0 potential allows the formation of a BI that is in thermal contact with a reservoir when the lattice is shallow, and isolated when the lattice is deep. When using the flattened volcano-shaped potential, we find that the quality of the separation between system and reservoir deteriorates if the plateau surrounding the crater becomes too large, because some atoms may remain in the region with no potential gradient.

Heating in the BI

Heating processes in a BI are strongly suppressed because of the vanishing density of states, and the only active processes must excite atoms into higher bands. Relevant heating mechanisms include incoherent light scattering from the optical lattice, intensity and position noise of the optical lattice, and background gas collision. To quantify the loss, we hold the BI for a variable duration of up to 1,600 ms and measure the total density n using both parity-projected imaging and full charge-resolved imaging as a probe of BI fidelity. In the parity-projected imaging, we measure the defect singlon density in the long-spacing lattice. In the full charge-resolved imaging, we measure the density after splitting the doublons into singlons in the short-spacing lattice. We find that the loss rate of density in the lattice centre is dn_r=6/dt = 5.1(3)% s⁻¹ using full charge-resolved imaging, and dn_r=6/dt = 4.8(4)% s⁻¹ using parity-projected imaging, assuming that the detection of a singlon corresponds to the loss of a single particle (Extended Data Fig. 3c,d). The zero-time intercept extracted from charge-resolved imaging is n = 1.983(3). The intercept from parity-projected imaging is n = 0.008(4), which is consistent with the directly measured singlon density. The difference between the parity-projected measurement and the charge-resolved measurement is consistent with the limitations imposed by imaging fidelity. Given the loading time of 100 ms, the above loss rate is consistent with the measured BI fidelity of F_BI,r=6 = 99.3(2)%.

Calibration of Hubbard interaction U

Owing to light-assisted collisions, in the short-spacing lattice, we can only perform parity-projected density imaging, and therefore detect the density of singly occupied sites \(n_\rms,det\) (ref. ⁶³). We correct the detected singlon density by the imaging fidelity to estimate the actual singlon density n_s. At half-filling (Figs. 2 and 3), the singlon density is a function of interaction and temperature: n_s(U, T). We rely on numerical simulations using DQMC to obtain the doublon density n_d(U, T) and compute the singlon density as n_s(U, T) = 1 − 2n_d(U, T). We find that n_d(U, T) is sensitive to interaction strengths but has only a weak dependence on temperature for 0.15 < T/t ≤ 0.25 and saturates for T/t ≤ 0.15 (Extended Data Fig. 4c). Using both the singlon density and spin correlations \(C_\bfd^zz\), we estimate the possible ranges for interaction and temperature as 8 < U/t < 9 and T/t ≤ 0.15. The fact that n_d is insensitive to temperature, and therefore effectively becomes a function of only interaction, allows us to invert this equation of state to calibrate U/t using only the measured singlon density n_s. With U/t calibrated, we can then estimate the temperature using spin correlations (see section ‘Calibration of temperature T at half-filling’).

To obtain the doped data shown in Fig. 4, the lattice depths and magnetic fields are slightly different from the ones used to obtain the half-filling data shown in Fig. 3 (see section ‘Experimental methods’). Therefore, interaction strength U/t needs to be recalibrated for the doped systems. We adjust the amount of expansion to prepare a sample with half-filling n = 1 in the centre, which can be identified as the maximum of singlon density n_s as filling n is increased. We then apply the same calibration protocol described above to this half-filled state to obtain the Hubbard interaction U/t given by the lattice and scattering length parameters used for the doped systems.

There is no available numerical simulation for the large U/t Hubbard model at low temperatures, so a different approach is required to calibrate the interaction strength U/t for the data taken in the Heisenberg limit. We first perform measurements at 580 G in the same lattice configuration as the final data, and with T/t ≤ 0.15 such that the temperature dependence of the singlon density is negligible. The resulting measured value of the singlon density is n_s(580 G) = 0.898(7), corresponding to U/t = 8.3(4). Next, using a_s(620 G)/a_s(380 G) = 312/233 ≈ 2.18, we obtain U/t = 18.6(8). If we ignore the temperature dependence of the singlon density and compare with numerical linked cluster expansion data at T/t = 0.2 (ref. ⁶⁵), our measured singlon density of n_s(620 G) = 0.976(3) gives 19.4(1.7), which is consistent with the above measurement.

Estimation of doping

To convert singlon density n_s to density n, we rely on numerical simulations using CP-AFQMC to obtain the doublon density n_d(n, U, T) as a function of density, interaction strength and temperature. From this, we can compute the singlon density n_s(n, U, T) = n − 2n_d(n, U, T). Similar to half-filling, the variation of doublon density reduces with temperature T and becomes negligible for T/t ≤ 0.15 (Extended Data Fig. 4b).

We plot the experimentally measured spin correlations as a function of singlon density n_s together with numerically simulated spin correlations as a function of computed singlon density n_s(n, U, T) in Extended Data Fig. 3f. CP-AFQMC simulation data of n_d is not shown in the density range 0.85 < n < 1 because of poor convergence. Based on comparisons of the nearest-neighbour spin correlations, the data are consistent with temperatures of T/t ≤ 0.15 for all values of the doping for which CP-AFQMC is performed.

Taken in combination, the above observations allow us to invert the equation of state and estimate the doping δ = 1 − n(n_s, U, 0) using numerical simulations performed at T/t = 0, which have been studied systematically in previous works¹⁷.

Calibration of temperature T at half-filling

For the half-filled data taken at U/t = 8.3(2), good agreement between experimental and numerical data (Fig. 3) allows us to measure temperature using a physically motivated observable that aggregates information from spin correlations beyond nearest neighbours. Specifically, we consider the staggered magnetization m^z, which is defined as a sign-corrected average of the spin correlation function up to a cutoff d in bond distance:

We estimate the value of \(m_\textexp^z\), as well as the 1σ error \(\delta m_\textexp^z\) in this estimate, from bootstrapping, and compute the expected value of \(m_\rmnum^z\) as a function of temperature using the DQMC.

We check the effect of boundary conditions by obtaining DQMC numerical data on 12 × 12 and 16 × 16 square systems with open boundary conditions and PBCs (Extended Data Fig. 7a). PBCs tend to overestimate spin correlations \(C_d^zz\) at long range, whereas the difference between 12 × 12 and 16 × 16 data is not substantial for d ≤ 6. This motivates our choice of performing subsequent calculations using open boundary conditions and a 12 × 12 system.

Spin correlations are computed at U/t = 8 and U/t = 9 (Extended Data Fig. 7b), converted into magnetization \(m_\rmnum^z\) and interpolated to produce a continuous function of temperature and interaction strength \(m_\rmnum^z=f_U(T)\) (using cubic splines along T and linear functions along U). At a fixed value of U based on experimental calibrations, we convert our knowledge of the true experimental magnetization, which we model as a Gaussian random variable \(\widetildem^z \sim \mathcalN(m_\textexp^z,(\delta m_\textexp^z)^2)\), into temperature by computing the probability distribution function of \(\widetildeT=g(\widetildem^z)\), where g is the inverse of the interpolated numerical data, \(g(m^z)=f_U^-1(m^z)\) if m^z ≤ f_U(0), and g(m^z) = 0 if m^z > f_U(0). We report the mean value and the ±1σ confidence interval of the temperature distribution.

Experimental and numerical magnetizations and their associated temperature estimates are shown in Extended Data Fig. 7c,d. At the experimentally calibrated value of U/t = 8.3, increasing the bond cutoffs from d = 3 to d = 6 (Extended Data Fig. 7a, vertical dashed lines) does not change the inferred mean temperature of T = 0.05. This indicates a good agreement between numerical and experimental data at all ranges and confirms the calibrated interaction strength (Extended Data Fig. 7c). With a cutoff d = 3 on bond distance, below which numerical data only weakly depends on boundary conditions (Extended Data Fig. 7a), the inferred mean value of T/t varies by about 0.01 within the reported uncertainty on interaction strength U/t = 8.3 ± 0.2, with again a weak variation of the confidence interval. We report in the main text a temperature and asymmetric errors of \(T/t=0.05_-0.05^+0.06\) obtained with a cutoff d = 6, and a single notable digit capturing the overall magnitude of the systematic errors related to interaction calibration and finite-size simulation effects.

Calibration of tunnelling and lattice parameters

As described in section ‘Experimental methods’, the key step to ramp from a dimerized lattice to the short-spacing lattice is to ramp down the long-spacing lattice by reducing the X lattice depth and to ramp up the short-spacing lattice by increasing the \(\barX\) lattice depth. Ramping the interference time phase ϕ from 0 to π/2 eliminates tunnelling dimerization but introduces a potential offset between the A and B sublattices. The non-reciprocal attenuator allows for ϕ to be stabilized over a much larger range of X lattice depths, allowing us to suppress tunnelling dimerization without introducing potential offsets. We use the calibrated lattice depths and interference parameters^12,57 to numerically compute the band structure of the 2D lattices. The absolute amplitudes of tunnellings (in Hz) can then be computed by constructing maximally localized Wannier orbitals⁶⁶ or by fitting the band structure with a tight-binding model. We find that the two methods give consistent results for our lattice geometry (Extended Data Fig. 6a) and report the resulting tunnelling amplitudes in Extended Data Table 1.

The tunnelling dimerization is given by the interference term in the lattice potential, which scales as \(\sqrtV_x\). It is important to quantitatively determine the dependence of intra- and inter-dimer tunnelling energies t_d, t_i and the perpendicular tunnelling energy t_p on V_X. With lattice depths V_Y and \(V_X+V_\barX\) fixed, the variation of the different tunnelling energies with V_X is shown in Extended Data Fig. 6a. At the end of the ramp V_X = 3.2(3) × 10⁻⁵E_R, and the tunnelling energies are all balanced within systematic uncertainties. To obtain the doped data, the X is ramped down to V_X = 3.2(3) × 10⁻⁵E_R in the shallow lattice condition and kept the same for the rest of the experimental sequence.

Experimental verification

Adiabaticity of splitting at strong interaction

In the strong interaction limit U/t = 18.6(8), the adiabaticity is decided relative to the many-body spin gap for an ideal finite-size system with sharp open boundaries and homogeneous potentials. The gap separating the ground state and the Anderson tower of states scales as 1/L², whereas the gap for spin wave excitations scales as 1/L, where L is the linear system size^15,48. In the absence of heating, slower ramp speed results in more adiabatic evolution.

Experimentally, as we increase the ramp duration from 20 ms to 80 ms, crossing the critical point predicted by previous numerical works⁴⁷, we find the spin correlations in the final state reach saturation and do not increase (Extended Data Fig. 6g). We suspect that for longer ramp durations heating competes with the improvement of adiabaticity. Holding during or after the ramp results in strong heating, which manifests as a reduction of spin correlations. We also find that heating is related to the magnetic bias field. When holding in the middle of the ramp, the heating is much stronger at 620 G, where we operate to achieve U/t = 18.6(8), than at 550 G, where the BI is prepared. This hints at heating due to three-body processes, which are strongly enhanced as the scattering length a_s is increased.

The saturation of spin correlations with increasing ramp time is measured at the same DMD potential strengths as when the BI is formed. We find that with weaker DMD potentials, 20 ms ramps are no longer adiabatic and result in reduced singlon density and spin correlations (Extended Data Fig. 6g). This suggests that atoms are leaving the crater region. However, we do not have a complete understanding of this dynamical process because the time dependence of the magnetic field ramp also plays an important part. Higher magnetic bias fields lead to stronger interaction strengths, which compete against the confining potential and may alter the physics of the transport process.

Adiabaticity of splitting compared with tunnelling dimerization ramp

In a homogeneous Hubbard system at half-filling, or in a Heisenberg spin system, the adiabaticity criterion is determined by the speed of the ramp compared with the energy gap of spin excitations¹⁵. In our case the relevant ramp is of the tunnelling dimerization, which is controlled by the interference phase. Experimentally, at U/t = 18.6(8), we find that a ramp time longer than 5 ms is sufficiently adiabatic and allows intra- and inter-dimer spin correlations to equalize. Ramps with a duration of less than 1 ms are diabatic and result in clear deviations. This ramp has no detectable effects on longer-range correlations, which is probably decided by the rate of the previous ramp across the quantum critical point. For longer ramp times, we find significant heating when the DMD0 potential is not optimized, leading to atom transport. The coldest reported temperatures are, therefore, obtained by dynamically balancing the confinement of the DMD0 potential, the tunnelling energy and interaction strengths. At U/t = 8.3(2), we find that heating is much less problematic and choose a ramp time of 25 ms to ensure adiabaticity. A systematic study of the phase transition and the resulting requirements on adiabaticity would require proper flattening of the potential and site-resolved preparation of the initial BI.

Characterization of tunnelling dimerization in doped systems

The lattice phase stabilization is kept active between consecutive experimental sequences, and the interference time phase is maintained. The optical lattice position is, therefore, tracked at the single-site level in fluorescence atom images. This allows us to probe spin correlations in a bond-resolved manner (see section ‘Data analysis’). Different y, intra-dimer and inter-dimer tunnelling energies t_y, t_d, t_i lead to different superexchange interactions \(J_y,J_\rmd,J_\rmi=4t_y^2/U,4t_\rmd^2/U,4t_\rmi^2/U\) on the respective bonds, and thus different spin correlations. In Fig. 2, we show how ramping the interference time phase ϕ = π/2 eliminates the tunnelling dimerization and correlation imbalance in the Heisenberg limit. To obtain the doped data, at the end of the ramp to V_X = 3.2(3) × 10⁻⁵E_R (using the non-reciprocal attenuator), we observe that the y, intra-dimer and inter-dimer spin correlations agree to within statistical errors (Extended Data Fig. 6d). The density profile also shows no offset between the A and B sublattices, confirming the absence of potential offsets even with ϕ = 0 (Extended Data Fig. 6b,c).

Tunnelling dimerization has striking effects on the doped Hubbard systems. In contrast to the half-filled case, in which long-range correlations are negligibly affected by dimerization under the conditions V_X = 0.016E_R, ϕ = 0, the doped systems show only correlations within the dimers. This suggests that dimerization will lead to different physics in the doped Hubbard systems, so it is crucial to remove this dimerization to observe the physics of the isotropic doped Hubbard model.

Adiabaticity of expansion after splitting

Splitting a band insulating state naturally gives rise to a half-filled state. To obtain doped Hubbard systems, we decrease the DMD0 potential such that the atoms can expand out of the crater. The boundary of the expansion is set by the wall formed by the DMD1 potential. Expansion in this ring-shaped region can be strongly affected by the shape of the DMD0 potential. We find that a volcano-shaped DMD0 potential (Extended Data Fig. 1f) with a sharp, outward slope (in which the potential decreases as distance from the centre increases) optimizes the separation between the BI and the reservoir. However, it is more difficult to expand the atoms adiabatically with this potential. The sharp slope acts as a potential barrier separating the crater and the region closer to the DMD1 wall potential, which forms two potential minima in the radial direction. This is similar to the broken symmetry state in a double-well system. The initial BI state is elevated from the true ground state with a small gap given by the tunnelling amplitude between the double well, which is exponentially suppressed with increasing strength of the potential barrier created by DMD0. An alternative, classical picture is that as the atoms flow out of the crater, they will accelerate downhill on the sharp slope, which is not a reversible process and therefore not adiabatic. A bowl-shaped potential that increases until reaching the DMD1 wall as the radial distance from the centre increases alleviates the above issues but will trap additional atoms during the BI preparation leading to increased entropy of the initial state. To balance these considerations, we choose the flattened volcano-shaped potential as a compromise (Extended Data Fig. 1g). We confirmed that the energy gap during expansion is similar to the case in which the potential has an inward slope using exact diagonalization in one dimension.

Larger tunnelling and smaller U/t leads to more adiabatic expansion for fixed expansion duration, suggesting that shallow lattices are favourable. However, we find this does not hold true in the limit for which the lattices are almost fully extinguished. We perform round-trip measurements of the BI fidelity by first decreasing the lattice depths to the values used in expansion and then increasing the lattice depths back to those used to obtain the BI state. Excitations created during the ramp will manifest as singlon defects in the BI. We find a significant increase in the number of these defects when lattice depths are decreased to below 0.5E_R during expansion. As a result, we opt to use a lattice depth of 0.3E_R during expansion, which corresponds to about 20% of the lattice depth used to load the BI. We believe this behaviour is because of band gaps becoming smaller than the tunnelling energy, allowing diabatic excitations to higher bands. After ramping to these conditions, we start the splitting procedure, which merges the two lowest bands in the long-spacing lattice into a single band in the short-spacing lattice.

We experimentally investigate the dynamics during expansion by varying the duration of the expansion step. We measure the final spin correlations after reloading for the expansion times of τ_exp = 1 ms, 15.5 ms and 30 ms. No statistically significant variation is observed in these measurements (Extended Data Fig. 6e), suggesting that 1 ms is sufficient for the expansion to be adiabatic. This is consistent with the large bandwidth and Fermi energy of around 10 kHz during expansion. To further facilitate thermalization during expansion, and to allow the field to settle before reloading happens, we ramp the magnetic field from 550 G to 590 G during the expansion step, which increases the scattering length a_s from around 86a₀ to 295a₀, and set the expansion time to a much longer duration of 50 ms.

Adiabaticity of expansion with fixed duration

In Fig. 5, we show the adiabaticity of expansion in the long-spacing lattice with fixed duration in units of the tunnelling time ħ/t. The temperatures are obtained by comparing the d = 1 and d =  \(\sqrt2\) spin correlations \(C_d^zz\) averaged in the central half-filled region to DQMC simulations. The goal is to probe adiabaticity as a function of interaction strengths, independent of the absolute value of tunnelling amplitudes. Although expansion in deeper lattices may lead to more lattice heating because of the increased laser intensity and smaller tunnelling amplitudes, little heating was observed in previous work⁵⁷ involving measurements performed at similar lattice depths and ramp times as for the deepest lattice explored in Fig. 5 (η = 1). The increased kinetic energy scales at shallower lattices may also reduce the effects of potential disorder, whose contribution to expansion adiabaticity requires future studies. We also measured the adiabaticity of expansion with a fixed duration of τ = 120 ms as shown in Extended Data Fig. 3e, which corresponds to 18.5ħ/t for η = 1. We find similar heating as in Fig. 5a despite the holding time being about four times shorter. This suggests that diabatic heating and dissipative heating are occurring on a similar scale. According to Fig. 5b, however, 120 ms should be slow enough to incur only about 0.2t increase in temperature, even at η = 1 (it would correspond to roughly 4 ms in Fig. 5). This indicates that interactions probably play a part in inhibiting transport at τ = 120 ms by placing more stringent requirements on adiabaticity.

Thermalization of splitting at half-filling

To check whether the half-filled state in Fig. 3 has equilibrated, we added a hold time of τ_h = 0 ms, 10 ms, and 20 ms after ramping into the final antiferromagnetic state. During this measurement, the lattice alignment relative to the DMD potentials was not optimized, which may explain the higher resulting temperatures. We find no change in the singlon density as a function of radial distance r from the trapping potential centre, or in the overall profile of the spin correlations as a function of bond distance d (Extended Data Fig. 6h). However, we observe a slight decrease of the nearest-neighbour correlation, which may be attributed to heating during the hold time. This suggests that the ramp to split a BI into a half-filled system realizes a state in thermal equilibrium.

Thermalization during reloading

After unloading the BI, splitting into a half-filled Fermi liquid, and expanding into a Fermi liquid with filling n < 1, the sample is in a similar state to previous works^11,63, but at lower entropy. We reload the lattice using a linear ramp-up of the lattice depth in 100 ms, which is chosen to balance adiabaticity and lattice heating. Moreover, we experimentally confirmed the final quantum state is in equilibrium by holding for τ_h = 0 ms, 20 ms and 40 ms, corresponding to 0ħ/t, 20ħ/t and 40ħ/t. No statistically significant variation is observed for these hold times (Extended Data Fig. 6f).

Furthermore, in the doped system, we can cross-check the thermalization throughout the sample by comparing temperature estimates obtained at different locations in the cloud. As described in section ‘Data analysis’, the temperatures shown in the main text are obtained in an ROI with radii r = 3, 4 and 5 in the centre of the cloud by including only pairs of sites within the ROI (which we refer to as strict binning). We can also obtain temperature estimates from the radially averaged spin correlations, although these estimates suffer from averaging over larger potential variations and different bin shapes. Nevertheless, in Extended Data Fig. 8, we reanalyse the data from Fig. 4f to plot \(C_\rmbin^zz(d)\) against the measured singlon density n_s,bin. \(C_\rmbin^zz(d)\) denotes the measured zz spin correlation at bond distance d for the corresponding bin. Note that the above analysis does not apply strict binning, so only one of the two sites used to compute a given correlation function must be contained within the bin. This leads to systematic deviations from the results obtained with strict binning. For example, the correlations with longer bond distances will be underestimated for the bin with the shortest distances, as sites at lower densities are involved. Nevertheless, this analysis offers a qualitative view that the atom cloud has thermalized across different densities.

Exact diagonalization of BI splitting

We use the QuSpin package⁶⁷ to compute the evolution of energy levels during splitting with exact diagonalization. For the Heisenberg model (Fig. 2), we choose a system size of 6 × 5, with a PBC in the long direction and twisted boundary condition in the short direction. The twisted boundary condition is defined as connecting (i, 5) → ((i + 1)%6, 1). The spin exchange coupling along the y-direction is fixed to J = 1, and \(\alpha =\sqrtJ_\rmd/J=\sqrtJ/J_\rmi\) are varied from 10 to 1.

Numerical simulations at half-filling

Our simulations at half-filling were performed with finite-temperature DQMC and ground-state AFQMC methods. AFQMC and DQMC are numerically exact formulations for studying quantum many-body systems. The approach begins with the Trotter decomposition, which breaks the original imaginary-time propagator into smaller pieces. To handle the on-site interaction, an auxiliary field is introduced using the Hubbard–Stratonovich transformation, transforming the interaction operator into a sum of one-body operators. These steps allow the partition function to be expressed as a sum over the products of two Slater determinants—one for spin-up electrons and one for spin-down electrons—whose matrix elements can be computed analytically. However, the product may take both positive and negative values, leading to a sign problem (except in specific cases, such as the half-filled 2D repulsive Hubbard model, in which particle–hole symmetry eliminates this issue).

In our simulations (Fig. 3), finite-temperature results are obtained using the DQMC method with 7,000 thermalization sweeps, 200,000 measurement sweeps and a time step of Δτ = 0.05. Ground-state data are generated with the AFQMC method, using the Metropolis algorithm with force bias updates⁶⁸, thousands of sweeps and a time step of Δτ = 0.02. We verify that the Trotter error at these values of Δτ is smaller than the statistical error, ensuring the robustness of our results. To mitigate ergodicity issues and fluctuations in spin correlations caused by the SU(2) symmetry breaking in the spin-z Hubbard–Stratonovich transformation, we adopt the charge Hubbard–Stratonovich transformation for both the finite-temperature and ground-state calculations. Additionally, the infinite variance problem⁶⁹ in spin correlation measurements is significantly reduced when using the charge decomposition instead of the spin decomposition.

CP-AFQMC simulation

For doped systems, we use both finite-temperature^16,70 and ground-state⁷¹ CP-AFQMC methods to compute the properties of the system at zero and finite temperatures, respectively. The finite-temperature CP-AFQMC method shares several of the building blocks from the standard DQMC method, including the use of Trotter decomposition and the Hubbard–Stratonovich transformation. However, it introduces two key differences. First, in systems suffering from the sign problem, an exact condition is derived for the paths in auxiliary-field space that cause the sign problem⁷⁰. It is shown that only a small subset of paths in the auxiliary-field space contribute to the partition function. The remaining paths are symmetrically distributed and cancel each other, which adds noise to the computation of observables. To address this, the CP-AFQMC method imposes a constraint, acting as a gauge condition, to isolate and sample the relevant paths. This constraint is exact when the many-body Hamiltonian is used in the constraint. Second, to implement the constraint and sample configurations efficiently, the algorithm uses a branching random walk with importance sampling to construct complete paths. In practical applications, an effective Hartree–Fock Hamiltonian is used as a trial Hamiltonian to define the constraint¹⁶. The parameters U_eff and β_eff are tuned so that the spin correlations obtained by the effective Hamiltonian closely match those of the many-body system¹⁸.

Ground-state CP-AFQMC⁷¹ is a projection-based quantum Monte Carlo method that leverages the principle that the ground state can be accessed by applying an imaginary-time evolution operator to an initial wave function, provided the trial wave function has a nonzero overlap with the ground state. Similar to the finite-temperature algorithm, ground-state CP-AFQMC also combines the Trotter decomposition with the Hubbard–Stratonovich transformation to reformulate the imaginary-time evolution as a stochastic process—a random walk through the space of Slater determinants. Ground-state properties are calculated as statistical averages over the configurations sampled during this random walk. To address the fermion sign problem, an unrestricted Hartree–Fock solution is used as a trial wave function, introducing a constraint that ensures each Slater determinant in the random walk maintains a positive overlap with the trial wave function. Extensive benchmarks in the literature^21,23,27,28 demonstrate that CP-AFQMC delivers high accuracy for studying ground-state and finite-temperature properties of quantum many-body systems. Our ground-state AFQMC calculations followed similar procedures to ref. ¹⁷ (although at half-filling we applied the charge decomposition as discussed earlier). In our simulations (Fig. 4), the Trotter time step is typically 0.05 and 0.01 in finite temperature and ground-state calculations, and we verify that the Trotter errors are limited. The population of random walkers is around 5,000 in these calculations.

Quantum Monte Carlo for Heisenberg model

Finite-temperature numerical simulations of the Heisenberg model in Fig. 2 and Extended Data Fig. 9 are performed with the SpinMonteCarlo.jl package (www.juliapackages.com/p/spinmontecarlo), using a loop quantum Monte Carlo algorithm with 1,024 warmup updates and 8,192 measurement updates, over 16 × 16 dimerized lattice unit cells (512 sites) with PBCs. Individual spin correlators \(\langle S_z(\bfr)S_z(\bfr^\prime )\rangle \) are grouped by pairs of sites \((\bfr,\bfr^\prime )\) with the same bond vector \(\bfr-\bfr^\prime \), distinguishing pairs that belong to the same sublattice from those that do not. These correlators are averaged at each measurement update, resulting in a relative statistical error of the order of 10⁻³. The resulting correlation maps are shown in Extended Data Fig. 9a for representative values of the coupling parameter α at temperature T/J = 0.5. We estimate that the systematic errors due to finite-size effects are at most 5 × 10⁻³ in the square lattice at this temperature, based on a comparison to a 32 × 32 system.

Staggered magnetization m^z is obtained by averaging the sign-corrected spin correlations over bond distance (Extended Data Fig. 9b), in this case truncated to a square 13 × 13 region (Extended Data Fig. 9a), and matching the ROI used in the analysis of experimental data. We observe a distinct increase and temperature dependence of m^z at couplings above α = 0.65, which we attribute to the existence of a quantum phase transition to an antiferromagnetic phase at zero temperature. This critical value is comparable to ground-state Heisenberg simulations performed in similar dimerized lattice geometries⁴⁷—note that the parameter α in our work is defined as a ratio of tunnel couplings and is related to ratios of antiferromagnetic spin couplings in the equivalent Heisenberg model by a square root.

After normalizing experimental data by the square spin moment \(n_\rms^2\), where n_s = 0.95 is the averaged singlon density in this dataset, we observe good agreement between numerical Heisenberg data compared with bond distance and experimental spin correlations \(| \bfr-\bfr^\prime | \) in the square lattice at U/t = 18.6(8) (Extended Data Fig. 9c). A least-squares fit of correlations up to \(| \bfr-\bfr^\prime | \le 8\) results in an estimated temperature of T/J = 0.458(3).

Effective temperature in Hubbard systems compared with cuprates

The single-band Hubbard model can be related to the high-T_c superconducting cuprates through a few steps of reduction and approximation. A more realistic approximate model for the cuprates is the three-band Hubbard model, in which tunnelling t and interaction strength U can be correspondingly related to energy scales in cuprates². Therefore, it is not straightforward to relate the temperatures in the one-band Hubbard model with doping to an effective temperature in cuprates.

However, at half-filling, the physics is well understood in the Hubbard model³ and cuprates^2,19,20 and can be described by an antiferromagnetic Heisenberg model. In this regime, the characteristic energy scale is the exchange energy J, which can be readily probed in cuprates and is J = 4t²/U in the one-band Hubbard model. This correspondence allows us to convert the temperature in the half-filled Hubbard model using T/J to an effective temperature in cuprates. Taking J = 125(5) meV in yttrium barium copper oxide^19,20 and U/t = 8, a temperature of T/t = 0.25 corresponds to about 725 K, and a temperature of T/t = 0.05 corresponds to around 145 K.