Description of the zoster vaccine rollout in Wales
The live-attenuated zoster vaccine (Zostavax) was made available to eligible individuals in Wales through a staggered rollout system starting on 1 September 2013. Under this system, individuals aged 71 years or older were categorized into three groups on 1 September of each year: (1) an ineligible cohort of those aged 71 to 78 years (or 77 years, depending on the year of the program), who became eligible in the future; (2) a catch-up cohort, consisting of individuals aged 79 years (or 78 years, again depending on the year of the program); and (3) those who were ineligible as they were aged 80 years or older and who never became eligible.
Our analysis focused on adults born between 1 September 1925 (88 years old at program start) and 1 September 1942 (71 years old at program start). Those born between 1 September 1925 and 1 September 1933 never became eligible, whereas those born between 2 September 1933 and 1 September 1942 became progressively eligible in a catch-up cohort. Specifically, the vaccine was offered to those born between 2 September 1933 and 1 September 1934 in the first year of the program (1 September 2013 to 31 August 2014); those born between 2 September 1934 and 1 September 1936 in the second year (1 September 2014 to 31 August 2015); those born between 2 September 1936 and 1 September 1937 in the third year (1 September 2015 to 31 August 2016); and those born between 2 September 1937 and 1 September 1938 in the fourth year (1 September 2016 to 31 August 2017). As of 1 April 2017, individuals become eligible for the vaccine on their 78th birthday and remain eligible until their 80th birthday. Our analysis principally compared individuals born on or shortly after 2 September 1933, to individuals who never became eligible as they were born shortly before 2 September 1933. We show in Supplementary Figs. 26–28 that most eligible individuals, especially in the first two eligibility cohorts, which are the focus of our analysis, took up the vaccination during their first year of eligibility (as opposed to during later years) and that vaccination uptake in these first two eligibility cohorts was of a similar magnitude.
Data source
Healthcare in Wales is provided through the Welsh National Health Service (NHS), which is part of the United Kingdom’s single-payer single-provider healthcare system59. NHS Wales and Swansea University created the SAIL Databank26,60,61,62,63,64, which includes full electronic health record data for primary care visits linked to information on hospital-based care as well as the country’s death register data.
SAIL generates a list of all individuals who have ever been registered with a primary care provider in Wales (which is the case for over 98% of adults residing in Wales27) from the Welsh Demographic Service Dataset65. SAIL then links this universe of individuals to each of the following datasets. Electronic health record data from primary care providers is made available in SAIL through the Welsh Longitudinal General Practice dataset66, which contains data from approximately 80% of primary care practices in Wales and 83% of the Welsh population. These electronic health record data use Read codes, which provide detailed information on patients and their care encounters, including diagnoses, clinical signs and observations, symptoms, laboratory tests and results, procedures performed and administrative items67. Zoster vaccination was defined using both codes for the administration of the vaccine as well as product codes (Supplementary Table 1). Diagnoses made and procedures performed in the hospital setting (as part of inpatient admissions or day-case procedures) are provided in SAIL through linkage to the Patient Episode Database for Wales68, which begins in 1991 and contains data for all hospital-based care in Wales as well as hospital-based care provided in England to Welsh residents. Procedures are encoded using OPCS-4 codes69 and diagnoses using ICD-10 codes70. Attendance information at any NHS Wales hospital outpatient department is provided through linkage to the Outpatient Database for Wales71, which starts in 2004. ICD-10-encoded diagnoses of cancers are identified through linkage to the Welsh Cancer Intelligence and Surveillance Unit72, which is the national cancer registry for Wales that records all cancer diagnoses provided to Welsh residents wherever they were diagnosed or treated. This dataset begins in 1994. Finally, cause-of-death data are provided for all Welsh residents (regardless of where they died in the United Kingdom) through linkage to the Annual District Death Extract73, which begins in 1996 and includes primary and contributory causes of death from death certificates. Dates for deaths were those on which the death was registered, as opposed to when it occurred. Cause-of-death data use ICD-9 coding until 2001 and ICD-10 coding thereafter.
When testing for any discontinuities in educational attainment across the date-of-birth eligibility threshold, we used a dataset provided by the Office for National Statistics (ONS)74. This dataset was generated by the ONS from the 2011 UK Census for all usual residents aged 16 or over, born in Wales between January 1925 and December 1950, regardless of their employment status. The data were categorized by the ONS by sex, month and year of birth (January 1925 to December 1950), highest level of qualification and occupation.
Ethics approval was granted by the Information Governance Review Panel (IGRP, application number, 1306). Composed of government, regulatory and professional agencies, the IGRP oversees and approves applications to use the SAIL databank. All analyses were approved and considered minimal risk by the Stanford University Institutional Review Board on 9 June 2023 (protocol number, 70277).
Study cohort, follow-up period and loss to follow-up
Our study population consisted of 296,603 individuals born between 1 September 1925 and 1 September 1942 who were registered with a primary care provider in Wales on the start date of the zoster vaccine program rollout (1 September 2013). As we only had access to the date of the Monday of the week in which an individual was born, we were unable to determine whether the individuals born in the cut-off week starting on 28 August 1933 were eligible for the zoster vaccine in the first year of its rollout. We therefore excluded 279 individuals born in this particular week. Among the remaining individuals, 13,783 had a diagnosis of dementia before 1 September 2013 and were therefore excluded from the analyses with new diagnoses of dementia as outcome. The size of our final analysis cohort for all primary analyses for new dementia diagnoses was therefore 282,541. This analysis cohort was used for all analyses except those with incidence of dementia before zoster vaccination program start, shingles and postherpetic neuralgia as outcomes; analyses for which we did not exclude individuals with a dementia diagnosis before 1 September 2013.
We followed individuals from 1 September 2013 to 31 August 2021, which allowed for a maximum follow-up period of 8 years. In our primary specification, we selected a follow-up period of 7 years (that is, until 31 August 2020) because this enabled us to include grace periods of up to 12 months while still keeping the follow-up period constant for individuals on either side of the date-of-birth eligibility cut-off. However, we also show all results for follow-up periods from one to eight years in one-year increments. Owing to the unique anonymized NHS number assigned to each patient, we were able to follow individuals across time even if they changed primary care provider. Patients were therefore only lost to follow-up in our cohort if they emigrated out of Wales or changed to one of the approximately 20% of primary care practices in Wales that did not contribute data to SAIL. Over our seven-year follow-up period, this was the case for 23,049 (8.2%) of adults in our primary analysis cohort, with no significant difference in this proportion between those born just before versus just after the 2 September 1933 eligibility threshold. In total, 92,629 (37.8%) of adults in our primary analysis cohort died during the seven-year follow-up period. Our primary analysis approach does not adjust for any competing risk of death for three reasons. First and foremost, in the absence of a zoster vaccination program, there is no reason that the competing risk of death should differ across the 2 September 1933 date-of-birth eligibility threshold. Second, not adjusting for competing risk of death in our setting is a conservative choice because eligibility for zoster vaccination may reduce (but is very unlikely to increase) all-cause mortality10,75. Thus, those eligible for zoster vaccination will, on average, be exposed to a longer time period during which they could become newly diagnosed with dementia. Third, to date, no well-established approach exists for survival analysis in a regression discontinuity framework, including the ability to determine the CACE and optimal bandwidth76.
Definition of outcomes
Owing to the neuropathological overlap between dementia types and difficulty in distinguishing dementia types clinically77,78,79, we chose to define dementia as dementia of any type or cause. Dementia was defined as a diagnosis of dementia made either in primary care (as recorded in the primary care electronic health record data), specialist care or hospital-based care, or dementia being named as a primary or contributory cause of death on the death certificate. The date of the first recording of dementia across any of these data sources was used to define the date on which the patient was diagnosed with dementia. Similarly, all other outcomes were defined using a diagnosis made in any care setting or mentioning as a primary or contributory cause of death. For chronic conditions, the date of the first recording across any of these data sources was used to define the date on which the chronic condition occurred. For non-chronic conditions or events (that is, shingles, postherpetic neuralgia, stroke, lower respiratory tract infections, falls, lower back pain, medication prescriptions, influenza vaccination and breast cancer screening), the date of first recording after the program date across any of these data sources was used for defining the occurrence of the outcome during the follow-up. The Read and ICD-10 codes used to define all outcomes are detailed in the Supplementary Codes.
Statistical analysis
The two authors who analysed the data (M.E. and M.X.) have coded all parts of the analysis independently. Occasional minor differences, resulting from different data coding choices, were resolved through discussion.
Our regression discontinuity approach
We used a regression discontinuity design to analyse our data, which is a well-established method for causal inference in the social sciences80. Regression discontinuity analysis estimates expected outcome probabilities just left and just right of the cut-off, to obtain an estimate of the treatment effect. We used local linear triangular kernel regressions (assigning a higher weight to observations lying closer to the date-of-birth eligibility threshold) in our primary analyses and quadratic polynomials in robustness checks. This is the recommended and most robust approach for regression discontinuity analyses even in situations in which the relationship between the assignment variable (here, date of birth) and the outcome is exponential81. An important choice in regression discontinuity analyses is the width of the data window (the bandwidth) that is drawn around the threshold. Following standard practice, we used an MSE-optimal bandwidth82, which minimizes the MSEs of the regression fit, in our primary analyses. We determined this optimal bandwidth separately for each combination of sample and outcome definition. In robustness checks, we examined the degree to which our point estimates vary across different bandwidth choices ranging from 0.25 times to two times the MSE-optimal bandwidth. We used robust bias-corrected standard errors for inference83.
Estimating the effect of being eligible for the zoster vaccine
In the first step, we determined the effect of being eligible for the zoster vaccine (regardless of whether the individual actually received the vaccine) on our outcomes. To do so, we estimated the following regression equation:
$${Y}_{i}=\alpha +{\beta }_{1}\times {D}_{i}+{\beta }_{2}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{o})+{\beta }_{3}\times {D}_{i}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{0})+{{\epsilon }}_{i},$$
(1)
where Yi is a binary variable equal to one if an individual experienced the outcome (for example, shingles or dementia). The binary variable Di indicates eligibility for the zoster vaccine and is equal to one if an individual was born on or after the cut-off date of 2 September 1933. The term (WOBi − C0) indicates an individual’s week of birth centred around the cut-off date. The interaction term Di × (WOBi − C0) allows for the slope of the regression line to differ on either side of the threshold. The parameter β1 identifies the absolute effect of being eligible for the vaccine on the outcome. Wherever we report relative effects, we calculated these by dividing the absolute effect estimate β1 by the mean outcome just left of the date-of-birth eligibility threshold, that is, the estimate of α.
Estimating the effect of actually receiving the zoster vaccine
In the second step, we estimated the effect of actually receiving the zoster vaccine on our outcomes. This effect is commonly referred to as the complier average causal effect (CACE) in the econometrics literature84. As is standard practice84, we used a fuzzy regression discontinuity design to estimate the CACE. Fuzzy regression discontinuity analysis takes into account the fact that the vaccine is not deterministically assigned at the week-of-birth cut-off. Instead, a proportion of ineligible individuals still received the vaccine and a proportion of eligible individuals did not receive the vaccine. To account for this fuzziness in the assignment, the fuzzy regression discontinuity design uses an instrumental variable approach, with the instrumental variable being the binary variable that indicates whether or not an individual was eligible to receive the vaccine, that is, is born on or after 2 September 1933. As we verify in our plot of vaccine receipt by week of birth (Fig. 1a), individuals who were born immediately after the date-of-birth eligibility threshold had a far higher probability of receiving the zoster vaccine compared with those born immediately before the threshold. Other than the abrupt change in the probability of receiving the zoster vaccine, there probably is no other difference in characteristics that affect the probability of our outcomes occurring between those born immediately after versus immediately before the date-of-birth eligibility threshold. Thus, the indicator variable for the date-of-birth eligibility threshold is a valid instrumental variable to identify the causal effect of receipt of the zoster vaccine on our outcomes. To compare the probability of experiencing the outcome between those who actually received the zoster vaccine versus those who did not, the instrumental variable estimation scales the effect size for being eligible for the zoster vaccine by the size of the abrupt change in the probability of receiving the vaccine at the date-of-birth eligibility threshold. The size of the jump is estimated through the following first-stage regression equation:
$${V}_{i}=\gamma +{\theta }_{1}\times {D}_{i}+{\theta }_{2}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{o})+{\theta }_{3}\times {D}_{i}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{0})+{{\epsilon }}_{i},$$
(2)
where Vi is a binary variable indicating whether the individual received the zoster vaccine and θ1 identifies the discontinuous increase in vaccine receipt at the date-of-birth eligibility threshold. All other parameters are the same as in regression (1).
The CACE estimated by rescaling the effect of eligibility with the first-stage effect from equation (2) can be represented as an IV estimate for μ1 from the following second-stage regression:
$${Y}_{i}=\varphi \,+\,{\mu }_{1}\times {\hat{V}}_{i}+{\mu }_{2}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{o})+{\mu }_{3}\times {D}_{i}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{0})+{{\epsilon }}_{i},$$
(3)
where \({\hat{V}}_{i}\) is the predicted probability of zoster vaccine receipt obtained from the first-stage estimation from equation (2). This CACE, μ1, represents the (absolute) average causal effect of receiving the vaccine among compliers, that is, patients who take up the vaccine if and only if they are eligible.
To compute relative effect sizes, we first introduce some notation. Let R0,c be the mean outcome among unvaccinated compliers and R1,c the mean outcome among vaccinated compliers just at the threshold. By definition, the absolute CACE is μ1 = R1,c − R0,c and the relative effect is \(\frac{{\mu }_{1}}{{R}_{0,c}}\). To estimate the relative effect, we need an estimate for R0,c. While it is impossible to identify compliers individually, we can estimate means of their observable characteristics, including R0,c (ref. 85). Let R1 denote the mean outcome among all vaccinated individuals (including compliers) at the cut-off. Assuming no defiers exist (patients who get vaccinated if and only if they are not eligible), all vaccinated people are either compliers or always-takers (patients who get vaccinated irrespective of their eligibility). Thus, R1 is equal to the population-weighted average of the mean outcomes among vaccinated compliers and always-takers: R1 = Pc × R1,c + Pa × R1,a, where Pc and Pa are the population share of the compliers and always-takers and R1,a is the mean outcome among always-takers at the cut-off. Solving for R1,c yields \({R}_{1,c}=\frac{{R}_{1}-{R}_{1,a}\times {P}_{a}}{{P}_{c}\,}\). All right-hand-side quantities in this equation can be estimated from data. First, R1 and R1,a can be estimated, respectively, as α + β1 and α from re-estimating regression (1) only among vaccinated individuals. Second, Pa and Pc can be estimated, respectively, as \(\frac{\gamma }{{\theta }_{1}+\gamma }\) and \(\frac{{\theta }_{1}}{{\theta }_{1}+\gamma }\) from regression (2). Finally, we estimate R1,c by the above formula and R0,c = R1,c − μ1. The relative effect is estimated as \(\frac{{\mu }_{1}}{{R}_{0,c}}\). All regressions involved in these steps can be stacked and jointly estimated, so that the relative effect is expressed as a differentiable function of known estimators a 95% confidence interval of the relative CACE can be estimated using the delta method86.
Analyses to investigate whether another intervention used the identical date-of-birth eligibility cut-off
Our analysis can only be confounded if the confounding variable changes abruptly at the 2 September 1933 date-of-birth eligibility threshold such that individuals very close to either side of this threshold would no longer be exchangeable with each other. The most plausible scenario of such a confounding variable would be the existence of an intervention that used the exact same date-of-birth eligibility threshold as the zoster vaccine rollout and that also affected the probability of a dementia diagnosis during our follow-up period. We conducted five analyses to demonstrate that the existence of such an intervention is unlikely, by establishing that measures of outcomes and behaviours that would be affected by such an intervention are smooth across the date-of-birth eligibility cut-off.
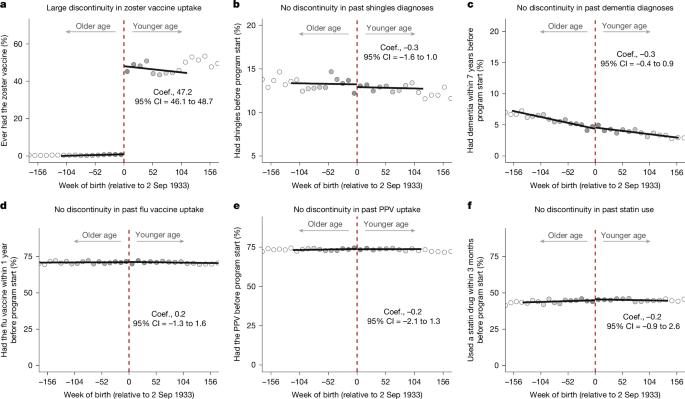
First, across a range of birthdates around the 2 September 1933 eligibility threshold, we plotted the probability of having received the following diagnoses or interventions before the start of the zoster vaccine program (on 1 September 2013): diagnosis of shingles, influenza vaccine receipt in the preceding 12 months, receipt of the pneumococcal vaccine as an adult, current statin use (defined as a new or repeat prescription of a statin in the 3 months preceding program start), current use of an antihypertensive medication (defined as a new or repeat prescription of an antihypertensive drug in the 3 months preceding the program start), participation in breast cancer screening (defined as the proportion of women with a record of referral to, attendance at or a report from breast cancer screening or mammography), each of the ten leading causes of disability-adjusted life years and mortality for Wales in 2019 as estimated by the Global Burden of Disease Project33, and all comorbidities (except for AIDS, which falls under privacy-protected diagnoses not made available by the SAIL database) that are included in the widely-used Charlson Comorbidity Index34. Moreover, we used each of these conditions, gender, decile of Welsh Index of Multiple Deprivation56, as well as all input variables to the Dementia Risk Score (as recorded before 1 September 2013)32, to predict the probability (while imputing a fixed age) of a new dementia diagnosis for each patient in the MSE-optimal bandwidth in our primary regression discontinuity analysis for dementia. In addition to plotting these predicted probabilities across a range of birthdates around the 2 September 1933 eligibility threshold, we also plotted the distribution of these predicted probabilities for patients who were eligible versus patients who were ineligible for zoster vaccination. The Read codes for each of these variables are provided in Supplementary Tables 1 and 2. As is the case for balance tables in clinical trials, these plots provide reassurance that individuals close to either side of the 2 September 1933 eligibility threshold are likely to be exchangeable with each other.
Second, we conducted the same analysis as we did for individuals with birthdays on either side of the 2 September 1933 threshold also for people with birthdays around 2 September of each of the three years of birth preceding and succeeding 1933. For example, when moving the start date of the program to 1 September 2011, we started the follow-up period on 1 September 2011 and compared individuals around the 2 September 1931 eligibility threshold. To ensure the same length of follow-up in each of these comparisons, we had to reduce the follow-up period to 5 years for this set of analyses. Thus, as an additional check, we shifted the start date of the program to 1 September of each of the six years preceding (but not succeeding) 2013, which enabled us to maintain the same seven-year follow-up period as in our primary analysis. If another intervention that affects dementia risk also used the 2 September threshold to define eligibility, we may then expect to observe effects on dementia incidence for these comparisons of individuals just around the 2 September thresholds of other birth years.
Third, we conducted the identical comparison of individuals around the 2 September 1933 date-of-birth threshold as in our primary analysis, except for starting the follow-up period 7 years before the start of the zoster vaccine program rollout. If there was an intervention that used the 2 September 1933 date-of-birth eligibility threshold but was implemented before the rollout of the zoster vaccine program, then we may expect to see an effect of the September 1933 threshold on dementia incidence in this analysis.
Fourth, we verified that the effects that we observed in our analyses for dementia incidence appear to be specific to dementia. If an intervention that used the exact same date-of-birth eligibility threshold as the zoster vaccine program indeed existed, it would be unlikely to only affect dementia risk without also having an influence on other health outcomes. We therefore conducted the same analysis as for when using dementia incidence as the outcome but for each of the ten leading causes of disability-adjusted life years and mortality in Wales in 2019 for the age group 70+ years33, as well as all conditions that are part of the Charlson Comorbidity Index34.
Fifth, we tested for discontinuities in educational attainment at the 2 September 1933 date-of-birth threshold using data from the 2011 census in Wales74. If an educational policy had used a 2 September (or specifically 2 September 1933) date-of-birth threshold and the policy was effective in increasing educational attainment, we would then expect discontinuities at the 2 September 1933 threshold in the attained education level between eligible and ineligible individuals. We used the identical analysis approach for this balance test as for our primary analyses in the SAIL database, except that we computed ‘honest’ confidence intervals based on the approach by Armstrong and Kolesár because the assignment variable (month of birth) in these data was monthly, and therefore coarser than the assignment variable (week of birth) in our analyses in the SAIL database87,88. This approach guards against potential vulnerability to model misspecification and resulting under-coverage of confidence intervals computed with more standard methods. These honest confidence intervals are conservative in the sense that they have good coverage properties irrespective of whether the functional form in the regression discontinuity analysis is misspecified, provided that the true functional form falls within a certain class of functions. For this class, we considered a function class defined by bounds on the second derivative of the conditional expectation function mapping date of birth to the probability attaining a certain educational level. We used conservative bounds of the respective curvatures by relying on global estimation of higher-order polynomials as proposed by Armstrong and Kolesár88.
Robustness to a different analytical approach
We additionally used a difference-in-differences instrumental variable approach (DID-IV) to confirm the findings from our regression discontinuity design because, in contrast to the regression discontinuity analysis, this approach does not rely on the continuity assumption (that is, the assumption that potential confounding variables do not abruptly change at precisely the date-of-birth eligibility threshold for the zoster vaccine program). To do so, we restricted our sample to patients born between 1 March 1926 and 28 February 1934. This sample consists of 96,767 adults, of whom 7,752 (8.0%) were eligible for, and 3,949 (4.1%) actually received, zoster vaccination. We then divided our sample into yearly cohorts centred around 1 September (that is, a cohort is all patients born between 1 March of one year and 28 February of the following year). Finally, we divided each yearly cohort into a pre-September birth season and a post-September birth season. Using a difference-in-differences approach, we then compared the outcome (new diagnoses of dementia) between patients born in pre- and post-September birth seasons and across yearly cohorts. More precisely, we tested whether the difference in outcomes across birth seasons is different for the 1933/1934 cohort than for the other cohorts. In doing so, we exploit the fact that zoster vaccination eligibility only differs between the two birth seasons in the 1933/1934-cohort but not in other cohorts, while accounting for the possibility that pre-September and post-September birth seasons may be systematically different for other reasons.
Our difference-in-differences setup implies that the interaction between the post-September birth season indicator and the 1933/1934-cohort indicator constitutes an instrumental variable for receipt of the zoster vaccine, enabling us to estimate the CACE (that is, the effect of actually receiving the vaccine among the compliers). This DID-IV approach relies on two important assumptions. As per the standard exclusion restriction assumption of IV analyses, the IV component of our DID-IV approach assumes that vaccine eligibility affects the outcome solely through a change in actual vaccine receipt. The DID component of our DID-IV approach assumes that, in the absence of the vaccine eligibility rule, the between-birth-season difference in vaccine uptake and in dementia incidence would have been the same in the 1933/1934 cohort as in the other cohorts. To investigate the validity of this assumption, we plotted the mean vaccine uptake and dementia incidence with 95% CIs by birth cohorts and birth seasons (Supplementary Fig. 29). As expected, we find that the between-birth-season differences in vaccine uptake diverge only in the 1933/1934 birth cohort. The absence of a between-birth-season difference in other birth cohorts supports the validity of our DID assumption.
To estimate the CACE in this DID-IV framework, we used two-stage least-squares regression. In the first stage, we identify the vaccine uptake due to the exogeneous change in vaccination eligibility by the following regression equation:
$${V}_{i}=\theta +\gamma \times {S}_{i}\times {C}_{i}+{\eta }_{m}+{\eta }_{c}+{{\epsilon }}_{i}$$
(4)
where Vi is a binary variable indicating patient i actually received the zoster vaccine. Si and Ci are binary variables indicating that patient i is born in the post-September birth season and in the 1933/1934 birth cohort, respectively. γ identifies the vaccine uptake due to the change in eligibility. θ, ηm and ηc are the constant term, birth month (January, February, …, December) and birth cohort (1926/1927, 1927/1928, …, 1933/1934) fixed effect, respectively. ϵi is the error term.
In the second stage, we estimate the effect of vaccine receipt by the following regression:
$${Y}_{i}=\alpha +{\beta \times \hat{V}}_{i}+{\eta }_{m}+{\eta }_{c}+{{\epsilon }}_{i}$$
(5)
where Yi is the outcome of patient i. \({\widehat{V}}_{i}\) is the probability of vaccine receipt predicted from the first-stage regression (4). The coefficient β identifies the CACE. α, ηm and ηc are the constant term, birth month and birth cohort (1926/1927, 1927/1928, …, 1933/1934) fixed effect, respectively. ϵi is the error term.
Robustness checks to different analytical specifications
We conducted a series of additional robustness checks. First, instead of starting the follow-up period for all individuals on 1 September 2013, we adjusted the follow-up period to account for the staggered rollout of the program by beginning the follow-up period for each individual on the date on which they first became eligible for the zoster vaccine (as described in the ‘Description of the zoster vaccine rollout in Wales’ section) (Supplementary Fig. 30). We controlled for cohort fixed effects in these analyses to account for the one- to two-year (depending on the year of the program) differences between cohorts in the calendar year in which this moving follow-up window started. That is, we defined one cohort fixed effect for ineligible individuals and the first catch-up cohort and then included additional cohort fixed effects for each group of patients who became eligible at the same time. Second, we varied our definition of a new diagnosis of dementia by implementing our analysis when defining dementia as a new prescription of donepezil hydrochloride, galantamine, rivastigmine or memantine hydrochloride. Third, we tested whether our results for the effect of being eligible for zoster vaccination on new diagnoses of dementia, shingles and postherpetic neuralgia hold across grace periods (that is, time periods since the index date after which follow-up time is considered to begin to allow for the time needed for a full immune response to develop after vaccine administration) of 0, 2, 4, 6, 8, 10 and 12 months (Supplementary Fig. 31). Fourth, we show our results with bandwidth choices of 0.25, 0.50, 0.75, 1.00, 1.25, 1.50, 1.75 and 2.00 times the MSE-optimal bandwidth (Supplementary Fig. 32). Fifth, we verified that our results are similar when using a local second-order polynomial specification instead of local linear regression.
Analyses to explore the effect mechanism
Changes in healthcare pathways as a result of a shingles episode
We conducted four analyses to examine this potential effect mechanism, the first three of which are described in detail in the main text. The fourth analysis was an event study that focused on the date of a shingles diagnosis during the follow-up period. Our event study compared the mean outcome in each month relative to the month before the date of the shingles diagnosis. Our regression model controls for changes over time (such as due to ageing of the study population or seasonal patterns in healthcare provider visits) using month-level fixed effects.
To implement our event study, we restricted our study population to those 56,098 individuals born within the MSE-optimal bandwidth of our primary regression discontinuity analysis for dementia. We then aggregated our event-level data into monthly longitudinal data, spanning September 2013 to March 2022. For each outcome of interest (as described in the main text), we then estimated the following event-study regression:
$$E[{Y}_{it}]={\beta }_{0}\sum _{k\ne -1}{\gamma }_{k}\times {D}_{k}\times {{\rm{shingles}}}_{i}+\,{\eta }_{i}+{\lambda }_{t},$$
(6)
where Yit is the outcome of interest for individual i in period t; shingles is a binary variable equal to one if the individual was diagnosed with shingles during the follow-up period; Dk are indicator variables for the k months before and after the shingles diagnosis (with k = −36, −35,…, 35, 36, and set to zero for individuals who were never diagnosed with shingles during the follow-up period); γk are the coefficients of interest, which capture the difference in the outcome in month k relative to the month before the shingles diagnosis; ηi is an individual-level fixed effect capturing time-invariant differences across individuals; and λt is a month-level fixed effect, capturing differences across periods. We used standard errors that allowed for clustering at the individual level, and therefore for autocorrelation.
Reduction in reactivations of the varicella zoster virus
We conducted four analyses to examine this potential effect mechanism. First, we implemented the identical regression discontinuity as in our primary analysis, except that we included a binary variable for being diagnosed with shingles during the follow-up period as a covariate. For the resulting estimate to be an unbiased measure of the degree to which the effect of zoster vaccination on dementia incidence is mediated by shingles diagnoses, there must be no variables that are related to both new dementia diagnoses and the probability of being diagnosed with shingles (that is, no confounding of the mediator-to-outcome relationship)89.
Second, to examine when during the follow-up period the dementia-delaying or dementia-preventing effect of zoster vaccination begins to emerge, we plotted Kaplan–Meier plots and (to account for competing risks) cumulative incidence curves among individuals born close to 2 September 1933. This analysis was based on the concept of local randomization28,29, which relies on exchangeability of individuals born immediately before versus immediately after 2 September 1933. To define the bandwidth for our analysis in which we could reasonably assume exchangeability across the threshold while maximizing statistical power, we used the widest bandwidth for which we achieved balance in baseline demographic and clinical characteristics of individuals eligible versus ineligible for zoster vaccination. We evaluated bandwidths ranging from 100% to 10% of the MSE-optimal bandwidth (90.6 weeks) in our primary regression discontinuity analysis in 10% decrements. The variables we used for our balance tests were the 14 variables listed in Supplementary Figs. 1 and 2 (except for the more sex-specific variables of past breast cancer screening, breast cancer and prostate cancer diagnoses) using a significance threshold of P < 0.05, while controlling for the false-discovery rate using the Benjamini–Hochberg procedure90. The largest bandwidth that achieved balance across all variables was 54.4 weeks.
Third, to investigate whether antiviral treatment during a shingles episode was associated with a reduction in the risk of dementia relative to not receiving treatment during a shingles episode, we restricted our study population to those individuals who received a diagnosis of shingles at any time after 1 January 2000 and had not received a diagnosis of dementia before 1 January 2000. Our exposure of interest in this analysis was whether or not an individual received a prescription of antiviral medication (acyclovir, famcyclovir, valacyclovir or inosine pranobex) within three months of the first shingles diagnosis. Individuals were followed up from the date of first shingles diagnosis until either the date of death, moving out of Wales, GP deregistration or end of data availability (1 March 2022). We then used a multivariable Cox proportional hazards model to regress diagnoses of dementia made after the date of the first recorded shingles episode onto whether or not the patient received an antiviral medication prescription for the first shingles episode. In a robustness check, we required that a new diagnosis of dementia must have been made at least 12 months after the date of the first shingles diagnosis. We adjusted our regressions for gender, restricted cubic splines (with three knots) of age at the first shingles infection, and the 12 variables in Supplementary Fig. 1 (excluding past breast and prostate cancer diagnoses).
Fourth, to explore whether experiencing recurrent shingles episodes was associated with a higher risk of dementia than having only a single episode, we used the same study population as in our analysis for treated versus untreated shingles. We matched individuals (via 1:1 propensity score matching) who had more than one shingles diagnosis (with the diagnosis dates having to be at least three months apart) after 1 January 2000 to individuals who only received a single shingles diagnosis after 1 January 2000. We matched individuals on proximity in the date of their first shingles diagnosis as well as the same list of baseline variables as for our analysis of treated versus untreated shingles, and forced an exact match on week of birth and gender. In each matched pair, we used the date of the second shingles diagnosis of the individual with more than one shingles diagnosis as the start date of the follow-up period. Using a Cox proportional hazards model, we then regressed new diagnoses of dementia made during the follow-up period onto whether or not the individual had received more than one shingles diagnosis. In a robustness check, we again required that a new diagnosis of dementia must have been made at least 12 months after the start date of the follow-up period.
VZV-independent immunomodulatory effect
To estimate the treatment effect heterogeneities described under this section in the main text, we fully interacted our fuzzy regression discontinuity model with a binary variable that indicates having the condition in question (for example, an autoimmune condition). Precisely, the fully interacted model was specified as:
$$\begin{array}{c}{Y}_{i}=\alpha +{\beta }_{1}\times {V}_{i}+{\beta }_{2}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{0})+{\beta }_{3}\times {D}_{i}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{0})\\ \,+{\beta }_{4}\times {V}_{i}\times {{\rm{H}}{\rm{E}}{\rm{T}}}_{i}+{\beta }_{5}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{0})\times {{\rm{H}}{\rm{E}}{\rm{T}}}_{i}\\ \,+{\beta }_{6}\times {D}_{i}\times ({{\rm{W}}{\rm{O}}{\rm{B}}}_{i}-{c}_{0})\times {{\rm{H}}{\rm{E}}{\rm{T}}}_{i}+{\beta }_{7}\times {{\rm{H}}{\rm{E}}{\rm{T}}}_{i}+{{\epsilon }}_{i}\end{array}$$
(7)
where the subscript i indexes individuals. Yi is a binary variable equal to 1 if an individual was newly diagnosed with dementia during the follow-up period. The binary variable Vi indicates receipt of the zoster vaccine. The binary variable Di indicates eligibility for the zoster vaccine (that is, born on or after 2 September 1933). The term WOBi − c0 indicates an individual’s week of birth centred around the date-of-birth eligibility threshold. The interaction term Di × (WOBi − c0) allows for the slope of the regression line to differ on either side of the date-of-birth eligibility threshold. The binary variable HETi is equal to one if an individual had the condition in question. Adding the terms (WOBi − c0) × HETi and Di × (WOBi − c0) × HETi allows the slopes to vary by this condition.
Vi and Vi × HETi are instrumented by Di and Di × HETi. Using the two-stage least-squares approach, the parameter β4 identifies the effect heterogeneity, that is, the difference in CACE on the outcome between patients with and without the condition. β1 and β1 + β4 identify the effect among compliers in the reference and comparison group, respectively. The estimates of the effects and heterogeneity are reported in absolute terms. To be consistent with our primary fuzzy regression discontinuity model (that is, without the HETi and interaction terms), we used local linear triangular kernel regressions and the MSE-optimal bandwidth from the primary model of the respective outcome.
For our analyses for autoimmune and allergic conditions, we used the 19 most common autoimmune conditions as defined previously91, and grouped the 11 least common conditions among them into a rare conditions category. We judged those conditions to be rare that had an incidence of less than 1% during the follow-up period in our cohort. These rare conditions included Addison’s disease, ankylosing spondylitis, Coeliac disease, Hashimoto’s thyroiditis, multiple sclerosis, myasthenia gravis, primary biliary cirrhosis, Sjögren’s syndrome, systemic lupus erythematosus, systemic sclerosis and vitiligo. For common allergic conditions, we used those defined previously92.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.