A map of the rubisco biochemical landscape

Strains

We cloned in a combination of E. coli TOP10 cells, DH5α and NEB Turbo cells. Protein expression was carried out using BL21(DE3). Δrpi was produced previously⁷ from the BW25113 strain. An rpiB knockout was obtained from the Keio collection. rpiA and the edd gene were knocked out through P1 transduction and subsequent curing of the kanamycin marker with pCP20 (ref. ³²). The result of these three knockouts, ΔrpiABΔedd, was Δrpi. The EDD deletion makes the strain rubisco dependent when grown on gluconate—a feature we did not make use of in this study.

Plasmids

Sequences and further details about plasmids used in this study can be found in Supplementary Data 3.

pUC19_rbcL

The rubisco mutant library was assembled in a standard pUC19 vector. This plasmid was used as a PCR template for each of the 11 sub-library ligation destination sites.

NP-11-64-1

Selections were conducted using a plasmid designed for this study with a p15 origin, chloramphenicol resistance, LacI controlling rubisco expression, TetR controlling PRK expression and a barcode.

NP-11-63

Protein overexpression in BL21(DE3) cells was conducted using pET28 with a SUMO domain upstream of the expressed gene⁶. pSF1389 is the plasmid that expresses the necessary SUMOlase, bdSENP1, from Brachypodium distachyon.

Primers

All primers were purchased from IDT and the oligonucleotide pool was purchased from Twist Bioscience. For sequences, see Supplementary Data 3.

Library design and construction

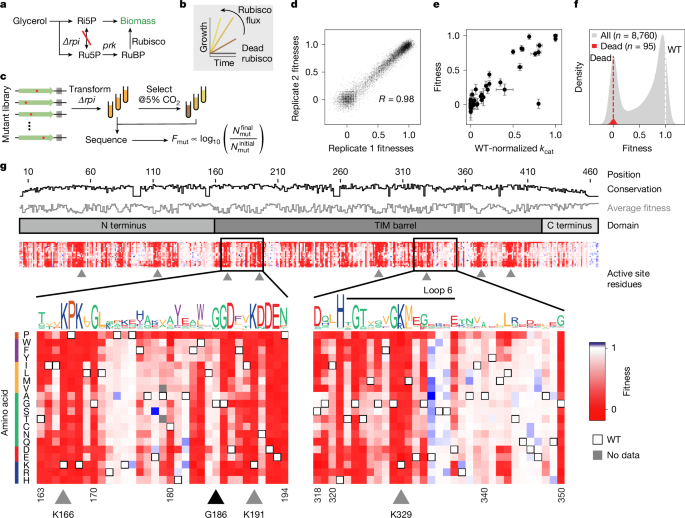
The R. rubrum rubisco sequence was codon-optimized for E. coli and mutated systematically by means of the scheme outlined in Extended Data Fig. 3. The rubisco gene was split into 11 pieces. For each of those pieces (around 200 base pairs (bp) each) all point mutants were designed and synthesized as oligonucleotide pools. Eleven oligo sub-library pools, containing all single mutants within their respective region of around 200 bp, were purchased from Twist Bioscience and each sub-library was amplified individually using Kapa Hifi polymerase with a cycle number of 15. Each rubisco gene fragment was inserted into a corresponding linearized pUC19 destination vector, containing the remainder of the rubisco sequence flanking the insert, through golden gate assembly. This assembly generated 11 sub-libraries of the full-length R. rubrum rubisco gene, with each sub-library containing a region of approximately 200 bp including all single mutants. Each of these 11 rubisco libraries were transformed separately into E. coli TOP10 cells and, in each case, more than 10,000 transformants were scraped from agar plates to ensure oversampling of the roughly 1,000 variants in each sub-library. Plasmids were purified from each sub-library and mixed together at equal molar ratios to generate the full protein sequence library.

To produce the final library for assay, a selection plasmid containing an induction system for rubisco and PRK (Tac- and Tet-inducible, respectively) was amplified with primers that included a random 30 nucleotide barcode. The linearized plasmid amplicon and the library were cut with BsaI and BsmBI, respectively, ligated together and transformed into TOP10 cells. Plasmid was purified by scraping around 500,000 colonies and transformed in triplicate into Δrpi cells. These transformations were grown in 2× yeast extract tryptone medium to log phase (optical density (OD) = 0.6) and frozen as 25% glycerol stocks.

Bacterial growth analysis

Bacterial strains were grown overnight in 2× yeast extract tryptone medium to saturation and then backdiluted. Once cultures reached exponential growth (0.3 < OD₆₀₀ < 0.8) they were diluted into 150 μl of M9 media in 96-well plates with 25 μg ml⁻¹ chloramphenicol and the indicated concentrations of anhydrotetracycline and IPTG to a final OD₆₀₀ of 0.005 or 0.0005. Growth was monitored in a Spark plate reader (Tecan) while maintaining 37 °C and the indicated O₂ and CO₂ concentrations. Shaking consisted of alternating 5 min of orbital and 5 min of double orbital modes and measurements were collected every 10 min. Growth yields were calculated up to 40 h and growth rates were calculated as the growth rate between OD₆₀₀ values of 0.001 and 0.01 (the most consistently exponential range in our curves).

Long-read sequencing analysis

The plasmid library was cut with SacII and sent for Sequel II PacBio sequencing. Reads were aligned and grouped by their barcodes. All reads of a given barcode were aligned and a consensus sequence was obtained using SAMtools³³. Consensus sequences were retained if they were WT or had one mutation that matched the designed library. Any mutation in the backbone invalidated a barcode. A lookup table was generated to link each barcode to its associated mutation. The data analysis methods described in this study are publicly available at https://github.com/SavageLab/rubiscodms.

Library characterization and screening

Selections were performed by diluting 200 μl of glycerol stock with an OD of around 0.25 into 5 ml of M9 minimal medium with added chloramphenicol (25 μg ml⁻¹), glycerol (0.4%), 20 μM IPTG and 20 nM anhydrotetracycline. These cultures were grown in 11 ml culture tubes at 37 °C in a Percival AR-22 growth chamber at different CO₂ concentrations on a New Brunswick Scientific Innova 2000 shaker at 250 rpm at an angle of 60°. Cultures were grown until they reached an OD at 5 ml of 1.2 ± 0.2. This corresponds to a 100-fold expansion of the cells, that is, between six and seven doublings.

Cultures before and after selection were spun down and we lysed the cells and performed a standard plasmid extraction protocol using QIAprep Spin Miniprep Kit (Qiagen). Illumina amplicons were generated by PCR of the barcode region. These amplicons were sequenced using a NextSeq P3 kit.

Calculation of variant enrichment

Variant enrichments were computed from the log ratio of barcode read counts. The enrichment calculations include two processing parameters: a minimum count threshold (c_min) and a pseudo-count constant (α_p). The count threshold is the minimum number of barcode reads that must be observed either pre- or post-selection for the barcode to be included in the enrichment calculation. The pseudo-count constant is used to add a small positive value to each barcode count to circumvent division by zero errors. We use a pseudo-count value that is weighted by the total number of reads in each condition. For the jth variant and the individual barcodes, i, passing the threshold condition the variant enrichment is calculated as,

To identify optimal values for these parameters, we computed the variant enrichments across a two-dimensional parameter sweep of c_min and α_p to find the combination that resulted in the maximum mean Pearson correlation coefficient across all replicates at each condition. These were c_min = 5 and α_p = 3.65 × 10⁻⁷ (average of 0.3 pseudo-counts after multiplying by the total number of reads in each experiment, N_0,tot or N_f,tot), leading to a correlation coefficient of 0.978. Variant enrichment, e_j, was then calculated for every mutant using equation (1).

The variant enrichments were then normalized such that wild type has an enrichment value of 1 in all conditions and catalytically dead mutants have a median enrichment of 0. For the ‘dead’ variant enrichment, we computed the median enrichment for all mutations at the catalytic positions K191, K166, K329, D193, E194 and H287. The normalized enrichments at each condition were computed as

where e_j is the enrichment of the jth variant as given in equation (1), e_WT is the wild-type enrichment and \({\widetilde{e}}_{{\rm{dead}}}\) is the median enrichment across all mutants of the catalytic residues listed above.

Michaelis–Menten fits to enrichment data

The DMS library enrichments across different CO₂ concentrations were used to estimate Michaelis–Menten kinetic parameters for every variant. Guided by the linear relationship between growth rate and k_cat observed in Fig. 1e, we assume that the cell growth rate is proportional to the rubisco enzyme velocity to derive the CO₂ titration fits (see ‘Derivation of Michaelis–Menten fit’, equation (S1))

\({\widetilde{V}}_{\text{max},{\rm{mut}}}/{\widetilde{V}}_{\text{max},{\rm{WT}}}\) is the ratio of mutant maximum velocity relative to wild type, \({\widetilde{K}}_{{\rm{C}},{\rm{WT}}}\) is the wild-type K_C for which we used the value 149 μM, and \({\widetilde{K}}_{{\rm{C}},{\rm{mut}}}\) is the mutant K_C. The titration curves in triplicate for each variant were fit to equation (3) using non-linear least squares curve fitting while requiring both V_max and K_C,mut to be positive.

We noted that the \({\widetilde{K}}_{{\rm{C}}}\) fits to certain variants—particularly ones with low \({\widetilde{V}}_{\max }\)—were sensitive to the choice of processing parameters c_min and α_p. Given the semi-arbitrary nature of these parameters, this is clearly an undesirable dependence and engenders low confidence in the inferred \({\widetilde{K}}_{{\rm{C}}}\) values. To account for this uncertainty we conducted a parameter sweep (with 11 different c_min values linearly spaced between 0 and 50, and 10 α_p values log spaced between 1 × 10⁻⁹ and 1 × 10⁻⁶), and computed the variant enrichments for all combinations of these parameters. We then performed ten subsamplings of the replicates for all parameter sets and performed the ratiometric Michaelis–Menten fit. From this set of 1,100 \({\widetilde{K}}_{{\rm{C}}}\) fit values for each variant we computed a quartile-based coefficient of variation that was used as a figure of merit for the \({\widetilde{K}}_{{\rm{C}}}\).

Multiple sequence alignment

A multiple sequence alignment (MSA) of the broader rubisco family beyond Form II rubiscos was created using the profile HMM homology search tool jackhmmer³⁴. Starting with the R. rubrum rubisco sequence, jackhmmer applied five search iterations with a bit score threshold of 0.5 bits per residue against the UniRef100 database of non-redundant protein sequences³⁵. To compute phylogenetic conservation at each position, for each possible amino acid we computed the fraction of the total sequences that had that amino acid at the corresponding position of the MSA. The phylogenetic conservation is the maximum fraction, where the maximum is taken over all possible amino acids. Thus, if a position has an alanine in 90% of the sequences of the MSA, the phylogenetic conservation will be 0.9.

Protein purification

E. coli BL21(DE3) cells were transformed with pET28 (encoding the desired rubisco with a 14× His and SUMO affinity tag) and pGro plasmids (Takara). Colonies were grown at 37 °C in 100 ml of 2× yeast extract tryptone medium under kanamycin selection (50 μg ml⁻¹) to an OD of 0.3–1. Arabinose (1 mM) was added to each culture, which was then incubated at 16 °C for 30 min. Protein expression was induced with IPTG (Millipore) at 100 μM and cells were grown overnight at 18 °C. Cultures were spun down (15 min; 4,000g; 4 °C) and purified as reported⁶. In brief, cultures were spun down and lysed using BPER II (Thermo Fisher). Lysates were centrifuged to remove insoluble fraction. Rubisco was purified by His-tag purification using Ni-NTA resin (Thermo Fisher) and eluted by SUMO tag cleavage with bdSUMO protease (as produced in ref. ⁶). Purified proteins were concentrated and stored at 4 °C until kinetic measurement (within 24 h). Samples were resolved by SDS–polyacrylamide gel electrophoresis to ensure purity.

Rubisco spectrophotometric assay

Both k_cat and K_C measurements use the same coupled-enzyme mixture wherein the phosphorylation and subsequent reduction of 1,3-bisphosphoglycerate—the product of RuBP carboxylation—was coupled to NADH oxidation, which can be followed through 340-nm absorbance. Following Kubien et al.³⁶ and Davidi et al.⁶, the reaction mixture (Extended Data Table 1) contains buffer at 100 mM, pH 8, 20 mM MgCl₂, 0.5 mM dithiothreitol, 2 mM ATP, 10 mM creatine phosphate, 1.7 mM NADH, 1 mM EDTA and 20 U ml⁻¹ each of phosphoglycerate kinase, glyceraldehyde-3-phosphate dehydrogenase and creatine phosphokinase. Reaction volumes are 150 μl and samples are shaken once before absorbance measurements begin. Absorbance measurements are collected on a SPARK plate reader with O₂ and CO₂ control (Tecan). The extinction coefficient of NADH in the plate reader was determined through a standard curve of NADH solutions of known concentration (determined by a Genesys 20 spectrophotometer with a standard 1-cm path length, Thermo Fisher). Absorbance decline over time gives a rate of NADH oxidation and therefore a carboxylation rate. Because rubisco produces two molecules of 3-phosphoglycerate for every carboxylation reaction, we assume a 2:1 ratio of NADH oxidation rate to carboxylation rate.

Spectrophotometric measurements of k
_cat

The carboxylation rate constant (k_cat) of each rubisco was measured using methods established previously⁶. In brief, rubisco was activated by incubation for 15 min at room temperature with CO₂ (4%) and O₂ (0.4%) and added (final concentration of 80 nM) to aliquots of appropriately diluted assay mix (Extended Data Table 1) containing different 2-carboxy-d-arabinitol-1,5-bisphosphate (CABP) concentrations pre-equilibrated in a plate reader (Infinite 200 PRO; TECAN) at 30 °C, under the same gas concentrations. After 15 min, RuBP (final concentration of 1 mM) was added to the reaction mix and the absorbance at 340 nm was measured to quantify the carboxylation rates. A linear regression model was used to plot reaction rates as a function of CABP concentration. The k_cat was calculated by dividing the y intercept (reaction rates) by the x intercept (concentration of active sites). Protein was purified in triplicate for k_cat determination.

Spectrophotometric measurements of K
_C

Purified rubisco mutants were activated (40 mM bicarbonate and 20 mM MgCl₂) and added to a 96-well plate along with assay mix (Extended Data Table 1, in this case the same concentration of HEPES pH 8 buffer was used but EPPS can be substituted). Bicarbonate was added for a range of concentrations (1.5, 2.5, 4.2, 7, 11.6, 19.4, 32.4, 54, 90 and 150 mM). Plates and RuBP were pre-equilibrated at 0.3% O₂ and 0% CO₂ at room temperature. RuBP was added to a final concentration of 1.25 mM with water serving as a control for each replicate. NADH oxidation was measured by A₃₄₀ as in the k_cat assay. Absorbance curves were analysed using a custom script to perform a hyper-parameter search to choose a square in which to take the slope as carboxylation rate that best represented most of the monotonic decrease in A₃₄₀. K_C was derived by fitting the Michaelis–Menten curve using a non-linear least squares method. Error bars were determined depending on replicates: (1) multi day replicates: Michaelis–Menten fits were made for each replicate, s.e. and median were calculated on the basis of these fits. (2) Triplicates: absorbance data were fit to extract initial rates using different hyper-parameters and the median of these fits was used subsequently. Three different sets of initial rates were calculated on the basis of the technical replicates: one based on the median absorbance values, one based on the median minus the s.d., and one based on the median plus the s.d. Michaelis–Menten fits to these three sets of calculated rates were made and error bars show the difference between the low boundary, median and high boundary set.

Spectrophotometric measurements of K
_M,RuBP

K_M,RuBP was determined in a similar manner to k_cat and K_C. A titration of RuBP concentrations was used to generate rate-saturation curves under an atmosphere of 5% CO₂ and 0.5% O₂. Simple linear regression was used to fit the absorbance decays. K_M,RuBP was derived by fitting the Michaelis–Menten curve using a non-linear least squares method. Error was determined from the square root of the diagonals of the covariance matrix during fitting. The values from spectrophotometric assays are reported in Fig. 3f and Extended Data Figs. 6b,d and 9b.

Radiometric measurements of K
_C and k
_cat

¹⁴CO₂ fixation assays were conducted as in ref. ⁶ with minor modifications. Assay buffer (100 mM EPPS-NaOH pH 8, 20 mM MgCl₂, 1 mM EDTA) was sparged with N₂ gas. Rubisco, purified as described above, was diluted to around 10 μM (quantified using ultraviolet absorbance) in the assay buffer. It was then diluted with one volume of assay buffer containing 40 mM NaH¹⁴CO₃ to activate. Reactions (0.5 ml) were conducted at 25 °C in 7.7-ml septum-capped glass scintillation vials (Perkin-Elmer) with 100 μg ml⁻¹ carbonic anhydrase, 1 mM RuBP and NaH¹⁴CO₃ concentrations ranging from 0.4 to 17 mM (which corresponds to 15–215 μM CO₂). The assay was initiated by the addition of a 20-μl aliquot of activated rubisco and stopped after 2 min by the addition of 200 μl 50% (v/v) formic acid.

The specific activity of ¹⁴CO₂ was measured by performing a 1-h assay at the highest ¹⁴CO₂ concentration containing 10 nmol of RuBP. Reactions were dried on a heat block, resuspended in 1 ml water and mixed with 3 ml Ultima Gold XR scintillant for quantification with a Hidex scintillation counter.

The rubisco active site concentration used in each assay was quantified in duplicate by a [¹⁴C]-2-CABP binding assay. A 10-μl sample of the roughly 10 μM rubisco solution was activated in assay buffer containing 40 mM cold NaHCO₃ (final volume 100 μl) for at least 10 min. Then, 1.5 μl of 1.8 mM ¹⁴C-carboxypentitol bisphosphate was added and incubated for at least 1 h at 25 °C. [¹⁴C]-2-CABP bound rubisco was separated from free [¹⁴C]-2-CPBP by size exclusion chromatography (Sephadex G-50 Fine, GE Healthcare) and quantified by scintillation counting.

The data were fit to the Michaelis–Menten equation using the concatenated data of three to four experiments performed on different days. This assay was used to determine the values in Fig. 4c and Extended Data Fig. 9c.

Membrane inlet mass spectrometry determination of rubisco specificity

The method described in ref. ³⁷ was adapted for a membrane inlet mass spectrometry (MIMS) instrument (Bay Instruments). The O₂ ion signal was calibrated by measuring the 32 m/z ion at atmospheric O₂ and at ‘zero’ O₂. An atmospheric O₂ calibrant was achieved by equilibrating the MIMS buffer (200 mM Hepes pH 8, 100 mM NaCl, 20 mM MgCl₂) with air for 1 h at 25 °C. The ‘zero’ O₂ ion signal was determined by then adding approximately 5 mg Na₂S₂O₆ to the cuvette. CO₂ was calibrated by adding various amounts of NaHCO₃ to a solution of 100 mM HCl and recording the 44 m/z ion signal. In both cases, linear fits of ion counts to gas concentrations provided a simple conversion to determine gas concentrations and consumption rates. These calibrations had to be performed on every day in which the assay was used.

Rubisco enzymes were activated in 20 mM Hepes pH 8, 100 mM NaCl, 20 mM MgCl₂ and 20 mM NaHCO₃. Activated enzyme was added to 630 μl of MIMS buffer equilibrated with air at a concentration of 1.2 μM. Bovine carbonic anhydrase (Sigma Aldrich) was added at a final concentration of 0.3 mg ml⁻¹ and NaHCO₃ was added to a final concentration of 4 mM. The reaction was stirred in the sealed MIMS reaction chamber for approximately 2 min to collect a pre-reaction signal. The reaction was initiated by the addition of 2 mM RuBP. O₂ and CO₂ consumption rates were background corrected and converted to reaction velocities through conversion using the coefficients determined during calibration. Specificities were determined in triplicate by the following equation: S_C/O = ν_C[O₂]/ν_O[DIC], where DIC is the dissolved inorganic carbon pool.

Quantification of soluble enzyme concentration by immunoblotting

The Δrpi strain with wild-type rubisco was grown under selective conditions (overnight at 37 °C in M9 medium with 0.4% glycerol and 20 nM aTc) with varying IPTG concentrations at 5% CO₂ for 24 h. Afterwards, turbid cultures were centrifuged (10 min; 4,000g; 4 °C) culminating in roughly 20 mg pellet per sample. Pellets were lysed with 200 μl of BPER II and supernatant was transferred into a fresh tube and mixed with SDS loading dye. A Bio-Rad RTA Transfer Kit for Trans-Blot Turbo Low Fluorescence PVDF was used in combination with the Trans-Blot Turbo Transfer System. The PVDF membrane was carefully cut between 50 and 70 kDa post-blocking using a razor blade. Primary anti-RbcL II Rubisco large subunit Form II Antibody from Agrisera (1:10,000) and DnaK Antibody from Abcam (1:5,000) were incubated separately. Secondary horseradish-peroxidase-conjugated antibodies Donkey anti-mouse for DnaK (Santa Cruz Biotechnology) and Goat pAB to RB IgG horseradish peroxidase (Abcam were both used at 1:10,000). Subsequently, Bio-Rad Clarity Max Western ECL substrates were applied and the final results were imaged using a GelDoc (Bio-Rad).

Mutant fitness outlier

I190T (Fig. 1e) was the only outlier in our comparison of in vitro k_cat measurements from the literature and our fitness data. Because the value was reported without error estimates³⁸, we re-measured the k_cat of this mutant and found it to be 4.24 s⁻¹, which is 52% of the wild-type value, down from 80% previously reported. Still, the value seems to be anomalous compared with the rest of the trend (Extended Data Fig. 6b). One potential explanation is that the mutation at that position has a strong negative effect on protein expression. Another possibility, given that I190T is adjacent to the key active site lysine, K191, is that I190T causes a negative effect on lysine carbamylation that is, for some reason, more pronounced in vivo than in vitro.

Derivation of Michaelis–Menten fit

Following Stiffler et al.²⁰ we assume that the differences in bacterial growth rate are proportional to the differences in growth-limiting enzymatic activity.

Under the presumption of log-phase growth, the expected log ratio of reads after elapsed time t and normalized to the wild-type reads is given by

(Note that equation (S2) would also contain a normalization factor to account for the total number of reads obtained for the pre- and post-selection conditions. It is, however, a common factor for both the mutant and wild-type counts and therefore cancels out. Furthermore, the real analysis also includes pseudo-counts, which are omitted here in the derivation of the fit equation for simplicity. Substituting in the condition of exponential growth, that is, \({N}_{i,f}={N}_{i,0}\,{e}^{{\mu }_{i}{t}}\), and simplifying yields,

To normalize the enrichments, we divide by the log enrichment of the wild-type counts relative to the median enrichment of variants with mutated catalytic residues (and thus catalytically dead rubisco). We then add one for the convention that dead variants be centred at an enrichment of 0 and that wild-type be at an enrichment of 1. Thus, the normalized mutant enrichment is,

Then substituting equation (S3) we obtain,

Using the assumption in equation (S1) and the fact that the enzyme velocity of dead mutants is 0, we obtain the expected normalized enrichment as a function of the rubisco velocities,

Finally, using the Michaelis–Menten equation we obtain the predicted enrichments as a function of CO₂ concentration and the enzyme kinetic parameters.

Thus, in practice, we use equation (S7) as the fit equation to the normalized enrichment values for each variant across a range of CO₂ concentrations. For each we have, as fit parameters, the ratio of maximum velocities between the mutant and wild type, V_max,mut/V_max,wt, and the mutant K_C with the wild-type K_C set to the literature value of 149 μM.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.