A Drosophila computational brain model reveals sensorimotor processing

The Drosophila melanogaster central brain connectome, comprising more than 125,000 neurons and 50 million synaptic connections, allows brainwide analyses of how the fly processes sensory information^{1,2,11,12,13,14,15,16}. Although the Drosophila brain is comparatively small, a single Drosophila neuron may be connected synaptically to hundreds of downstream neurons, and interpreting how this connectivity relates to behaviour is not straightforward.

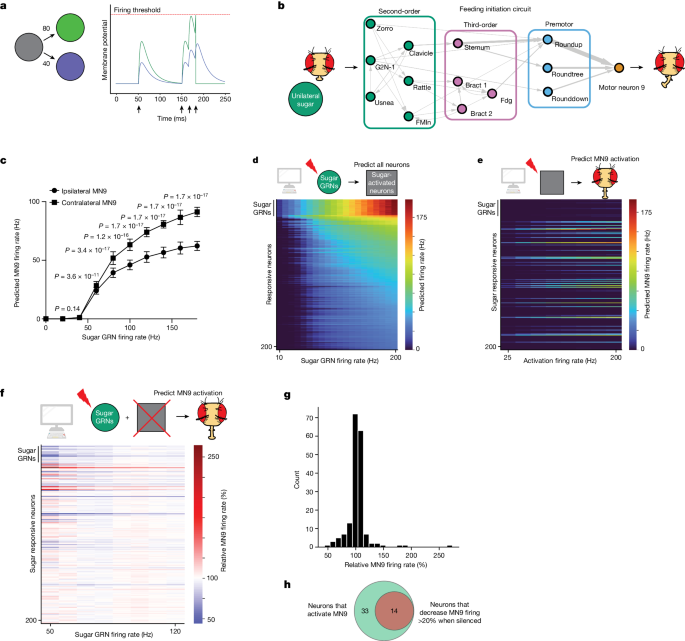
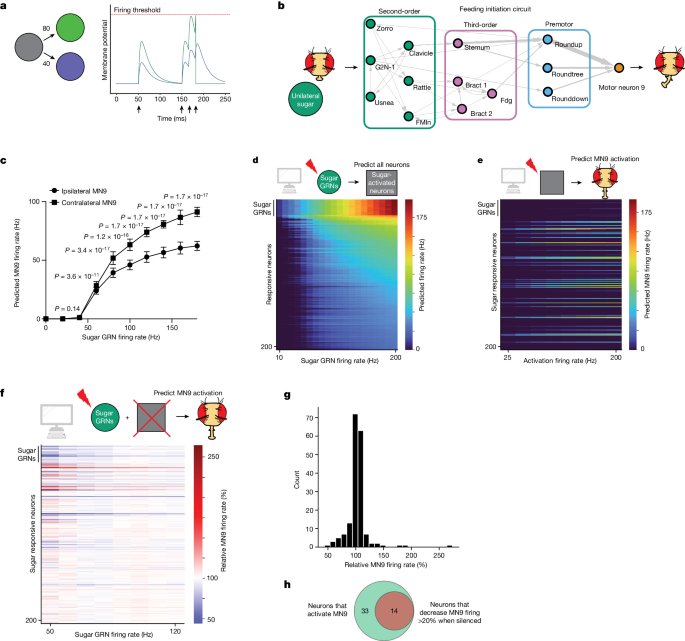
To model the neural circuit mechanisms that generate behaviour, we implement a simple leaky integrate-and-fire model using the connection weights derived from the entire adult Drosophila central brain connectome of reconstructed electron microscopy neurons^{1,17,18,19,20}, as well as neurotransmitter predictions for each neuron^3,21. In this model, spiking of a neuron alters the membrane potential of downstream neurons in proportion to the connectivity from the upstream neuron¹⁷ (Fig. 1a and Methods); if a downstream neuron’s membrane potential reaches the firing threshold, that neuron, in turn, fires.

a, Computational model schematic. Activation of the grey neuron at the times indicated by the arrows causes depolarization of the green and purple neurons in proportion to their connectivity from the grey neuron. Upon reaching the firing threshold, a neuron spikes, and its membrane potential is reset. b, Schematic of the proboscis extension response: unilateral sugar presentation causes proboscis extension towards the side of the fly with sugar. Arrow widths are proportional to the number of synapses connecting each set of neurons. c, Predicted MN9 firing rate of either the ipsilateral or contralateral MN9 in response to unilateral left hemisphere sugar GRN activation. Error bars represent s.d., Mann–Whitney U test. d, Heatmap depicting the predicted firing rates in response to unilateral 10–200 Hz sugar GRN firing. The y axis is ordered by firing rate at 200 Hz sugar activation, and depicts the top 200 most active neurons. e, Heatmap depicting the predicted MN9 firing rate when the top 200 responsive neurons are activated at 25–200 Hz; in d and e, the grey squares represent neurons that respond to sugar. f, Heatmap depicting the change in the contralateral MN9 firing rate in response to activation of sugar GRNs, while individually silencing each of the top 200 responsive neurons. The MN9 firing rate for each silenced neuron is normalized relative to the firing of MN9 when no neurons are silenced for each GRN activation frequency; In e and f, the y axis is ordered as in d. g, Histogram of the non-GRNs in f at 50 Hz. h, Venn diagram depicting the intersection between neurons predicted to activate MN9 and neurons predicted to cause a 20% decrease in MN9 firing when silenced.

We implemented this model in the spiking neural network simulator Brian2 (ref. ²²) using all Flywire neurons. The baseline firing of each neuron in our model is 0 Hz. All biophysical parameters are taken from previous D. melanogaster modelling or electrophysiology efforts^18,19, from the synaptic weights from the Flywire connectome^1,21 and from the neurotransmitter predictions³, except for W_syn—the single free parameter of the model, which corresponds to the magnitude of the change in downstream membrane potential that results from a single excitatory or inhibitory synapse (Methods). By driving activity in a sparse set of neurons, the model predicts changes in downstream firing.

We examined the model’s ability to predict circuit activity in two systems: feeding initiation and antennal grooming. We began by examining the Drosophila feeding initiation circuit because it has well-defined taste sensory inputs and motor outputs that are contained in the Flywire electron microscopy volume. Thus, computational modelling of the feeding initiation circuit permits analysis of an entire sensorimotor circuit, in contrast to other sensorimotor circuits that require descending neurons, which are incomplete in the Flywire volume. Furthermore, gustatory sensory neurons that respond to sugar, water and bitter tastes have been identified in the electron microscopy volume²³, permitting a detailed analysis of how these modalities interact. In addition, extensive experimental analysis provides a ground truth for computational studies^{4,5,23,24,25,26,27,28,29,30,31,32}. We further assessed the performance of the model in another well-defined but non-overlapping circuit—the antennal grooming circuit—as an independent evaluation of the model^6,7,8,9,10. As with the feeding initiation circuit, the antennal grooming circuit has well-defined sensory inputs, and a discrete, easily quantified behavioural output: antennal grooming behaviour. In both circuits, we tested specific predictions that the computational model generated using cell-type-specific genetic tools, optogenetics and functional imaging. We find that the model makes predictions consistent with our empirical observations, such as identification of neurons required for behavioural output. Thus, our computational model reduces the vast complexity of the connectome into simple, intuitive circuits.

In Drosophila feeding initiation, detection of appetitive substances in hungry flies results in proboscis extension and consumption³³. Gustatory receptor neurons (GRNs) on the body surface of the fly, including the labellum (tip of the proboscis) or the legs, respond directly to tastants and project to the primary taste centre of the insect brain—the suboesophageal zone (SEZ)^{23,33,34,35,36,37}. GRNs respond to specific taste categories, such as appetitive sugar or aversive bitter compounds, resulting in acceptance (that is, proboscis extension and feeding) or avoidance, respectively^24,33,35,38.To examine the neural circuits that influence feeding in response to taste detection, we focussed on four GRN categories: sugar, water, bitter and a fourth GRN category labelled by the ionotropic receptor Ir94e. Ir94e neurons respond to salt and the presentation of male genitals, but the exact tastants Ir94e neurons respond to are not well understood^31,33,37,38. These GRNs have been identified and classified previously in the electron microscopy brain volume²³; we verify and expand on this classification by clustering on the basis of connectivity and comparing this clustering with response properties of second-order neurons (Extended Data Fig. 1a–c and Methods).

When a fly encounters sugar, activation of appetitive GRNs results in activation of proboscis motor neurons (MNs) (Fig. 1b). The proboscis consists of three segments: the rostrum, the haustellum and the lip-like labella, controlled by the activity of 16 MNs³². We find that computational activation of labellar sugar-sensing GRNs activates several proboscis MNs involved in feeding, including MNs 6, 8, 9 and 11 (Fig. 1c, Extended Data Fig. 1d and Supplementary Table 1)³⁹. Consistent with the model’s predictions, MN9 and MN11 have been shown previously to respond to sugar stimulation in vivo^5,39. In total, we find that the computational model can model a complete sensorimotor transformation.

To assess the ability of our computational model to predict the composition and function of the feeding initiation circuit, we focussed specifically on the activity of MN9, which controls rostrum lifting during proboscis extension^5,32. The rostrum is the largest portion of the proboscis, permitting quantification of MN9 activity by measuring rostrum lifting. Although the exact correlation between MN9 firing rate and rostrum lifting is not known, we assume that increased MN9 firing rates correspond with increased rostrum lifting probability. Remarkably, unilateral sugar GRN activation activates the contralateral MN9 more strongly compared with the ipsilateral MN9 when either the left (Fig. 1c) or the right (Extended Data Fig. 1d) hemisphere GRNs are activated, consistent with behavioural experiments showing that unilateral taste detection on the legs promotes proboscis extension that is curved and directed towards the food source^26,40. Thus, we show that in silico sensory activation produces MN activity that is consistent with the observed behaviour of the fly taste sensorimotor circuit.

To confirm that our computational activation of MN9 depends on the actual connectivity weights determined from the fly connectome, we tested whether distorting synaptic weights would impair the ability of sugar sensory neurons to activate MN9. In these experiments, connectivity weights were shuffled randomly (while maintaining the global connectivity weight distribution). Although modelling using the correct connectome results in robust activation of MN9 in 100% of simulations when sugar-sensing neurons are activated at 100 Hz, only 1 of 100 shuffled simulations did (Supplementary Table 1d). Therefore, the predictive accuracy of our computational model depends on the actual connectivity weights of the fly connectome.

We next examined whether the computational model could accurately predict the neuronal cell types that are known to compose the feeding initiation circuit⁴. We first examined the neural network activated upon unilateral sugar GRN activation. We note that, given the variety of assumptions the model relies upon, absolute firing rate predictions are unlikely to be accurate; therefore, we examined network activity upon sugar GRN activation ranging from 10 to 200 Hz (Fig. 1d). We find that increasing sugar GRN firing rate increases activity of MN9, as well as MNs 6, 8 and 11. Of the 127,400 neurons modelled, we found that 45 are predicted to respond to 10 Hz sugar GRN activation, and 455 to 200 Hz (Supplementary Table 1). Activated neurons are defined as neurons that have greater than 0 Hz firing. Thus, the computational model predicts a large network activated by sugar taste detection that includes known sugar-responsive MNs.

Sugar taste detection influences activity in nutritive state and memory circuits, and modulates a broad range of behaviours, including feeding, oviposition and foraging^33,37,41. To specifically evaluate the subset of predicted sugar-responsive neurons that influence feeding initiation, we performed two further in silico experiments. First, as a strategy to identify neurons that drive feeding initiation, we computationally stimulated each of the top sugar-responding neurons in the network to identify those that drive activity in MN9 (Fig. 1e). Second, to identify neurons required for feeding initiation to sugars, we computationally activated sugar GRNs, silenced each of the top 200 sugar-responsive neurons one at a time, and measured the change in predicted MN9 firing (Fig. 1f,g). For these silencing experiments, we activated sugar-sensing neurons at frequencies ranging from 50 to 120 Hz in 10 Hz increments. Neurons that our model predicts to be required for feeding initiation will have decreased MN9 firing when silenced. We defined neurons predicted to cause a silencing phenotype as any neuron whose silencing causes MN9 firing to be 80% or lower compared with control MN9 firing at any of the eight sugar activation frequencies tested (50, 60, 70, …120 Hz; Fig. 1f). In general, silencing of individual neurons had the greatest effect when sugar GRNs were activated at low frequencies, implying greater redundancy in the circuit as sensory stimulation increases. In total, our analyses identified 47 neurons predicted to be sugar-responsive, and sufficient for feeding initiation. Of these 47 neurons, 14 are also predicted to be required for MN9 activity (Fig. 1h).

We next evaluated whether the predicted neurons for feeding initiation include neurons shown experimentally to participate in feeding initiation behaviour. Previous experimental studies identified ten neural classes that respond to sugar, and are sufficient for proboscis extension⁴ (Fig. 1b and Extended Data Fig. 2a–c). Our computational model correctly predicts that all ten cell types respond to sugar (Supplementary Table 2). Of these ten neurons, eight are predicted correctly to be sufficient to activate MN9 (ref. ⁴) (Supplementary Table 2). We previously found that five of the ten are required for sugar feeding initiation⁴ (Supplementary Table 2). Of these five, three are predicted by our computational model to cause a greater than 20% decrease in MN9 firing, and one of the others is predicted to cause a statistically significant decrease in MN9 firing, but less than 20%, when silenced. Although the model predictions generally match previous experimental results, there are some deviations. For example, the model fails to correctly predict that the Phantom cell type will activate MN9 (ref. ⁴) (Fig. 1e, Extended Data Fig. 2c and Supplementary Table 2). This cell type is predicted to be inhibitory. Phantom strongly synapses onto Scapula—a neuron that is also predicted to be inhibitory; Scapula, in turn, synapses onto Roundup, the pre-MN with the strongest predicted silencing phenotype. We speculate that activation of Phantom inhibits Scapula, potentially permitting Roundup and MN9 firing. Because the basal firing rate of all neurons in the model is 0, activation of inhibitory neurons in the model, in the absence of other input, cannot alter the firing of downstream neurons. A further explanation for incorrect predictions could be neuromodulation, which is not accounted for in our model. Particular neurons may be subject to neuromodulation, causing their activity to be different from predictions on the basis of connectivity. Alternatively, neurons that express neuromodulators may be poorly modelled. We speculated that the Usnea cell type, which has a strong experimental activation and silencing phenotype⁴ yet is not predicted to be either necessary or sufficient for proboscis extension, might be neuropeptidergic. To test this, we performed cell-specific knockdown of the gene Amontillado—a prohormone convertase required for neuropeptide processing in Drosophila^42,43. Knockdown of Amontillado phenocopied the Usnea silencing phenotype (Extended Data Fig. 1e), indicating that Usnea activity may require neuropeptide processing. Additionally, incorrect neurotransmitter predictions or other assumptions of the model may explain discrepancies between the prediction of our model and our experimental results. Despite these limitations, overall, this analysis demonstrates that our computational model correctly identifies known neurons in a sensorimotor circuit.

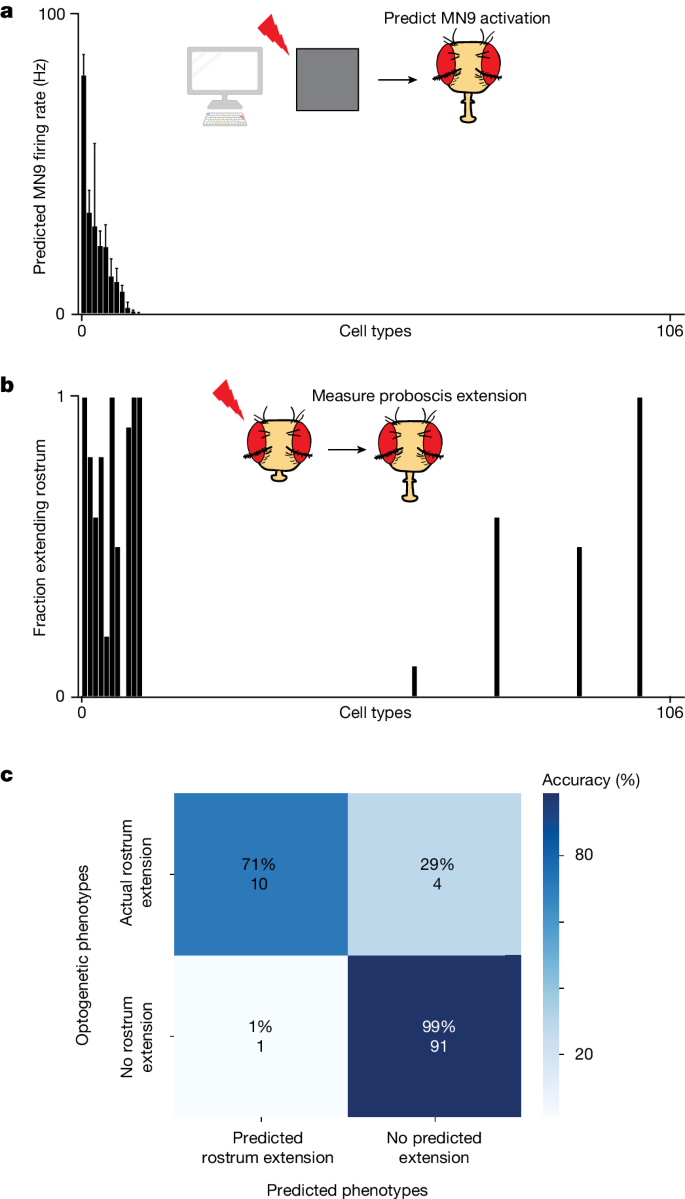
As an independent assessment of whether the computational model accurately predicts neurons that elicit MN9 activity, the output of our sensorimotor circuit, we compared optogenetic activation phenotypes with their corresponding computational activation phenotypes. To do this in a non-biased way, we performed a screen in which we optogenetically activated individual neuronal cell types with split-GAL4 lines and monitored the activity of MN9. The SEZ split-GAL4 collection labels 138 cell types in the SEZ—the primary feeding region of the brain⁴⁴. We identified 106 of these labelled cell types in the Flywire volume. Next, we crossed these split-GAL4 lines to create flies expressing the light-gated cation channel CsChrimson. We then optogenetically activated these neurons, and measured whether MN9 is activated by observing rostrum extension. We compared the predicted in silico MN9 activation phenotypes of these cell types when we activate them between 10 Hz and 200 Hz with the actual optogenetic activation MN9 phenotypes we observed. When we activate each cell type at 50 Hz, 11 are predicted to activate MN9 (that is, elicit MN9 firing greater than 0 Hz); notably, 10 of 11 of these cell types actually do elicit rostrum extension when optogenetically activated (Fig. 2a–c and Supplementary Table 3). Furthermore, of the 95 predicted not to elicit proboscis extension due to 50 Hz activation, just 4 have non-zero rostrum extension. Activation of these cell types at 200 Hz, rather than 50 Hz, results in the addition of five false positives. At 10 Hz activation, six cell types are predicted to cause MN9 activation; of these five, six do indeed cause proboscis extension. Thus, the computational model can predict the activation phenotypes of a non-biased sample of cell types at greater than 90% accuracy.

a, Predicted MN9 firing rates when each of 106 cell types are activated computationally at 50 Hz. Cell types are ordered by predicted MN9 firing rate. b, Fraction of flies extending the rostrum—the segment of the proboscis controlled by MN9—in response to optogenetic activation; cell types are ordered as in a. Where several split-GAL4 lines for a cell type were tested, the line with the highest extension rate is plotted; n = 10 flies per cell type. c, Confusion matrix showing the accuracy of MN9 activation predictions and the number of cell types in each category. The rostrum was predicted to extend if MN9 was predicted to have non-zero firing as a result of 50 Hz cell-type activation.

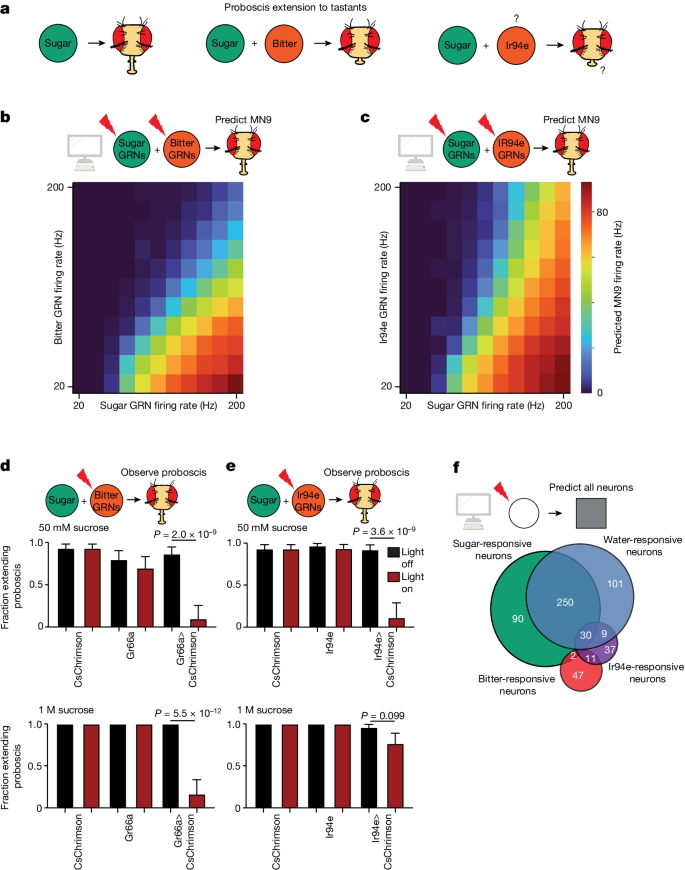
The accuracy of the model indicates that it provides a powerful platform to discover how different taste modalities are processed to influence feeding initiation. We first tested whether the model can predict the response to coactivation of both an attractive sugar stimulus and an aversive bitter stimulus. Bitter detection inhibits proboscis extension motor activity⁴⁵ (Fig. 3a). Indeed, the addition of bitter GRN activity to sugar GRN activation in our model resulted in an inhibition of MN6 and MN9 (Fig. 3b and Supplementary Table 4). We previously found, using calcium imaging, that bitter GRN activation inhibits the sugar pathway at the level of pre-MNs⁴, consistent with the predictions of the computational model (Supplementary Table 4).

a, Schematic outlining the previously known and unknown roles of sugar, bitter and Ir94e neurons. Question marks indicate that the exact substrate(s) that activate Ir94e neurons are not known, nor is it known whether Ir94e activation influences proboscis extension. b,c, Heatmap depicting the predicted MN9 firing rates in response to the combination of sugar GRN firing and bitter (b) or Ir94e (c) GRN activation. d,e, Fraction of flies exhibiting PER upon 50 mM sucrose stimulation or 1 M sucrose stimulation when Gr66a/bitter GRNs (d) or Ir94e GRNs (e) are optogenetically activated. Red bars indicate red light condition; n = 26–32, see Supplementary Table 9 for exact values. Mean ± 95% confidence intervals using Wilson’s score interval, Fisher’s exact test. f, Venn diagram showing the number and overlap of neurons that respond to sugar GRN (green) or water GRN (blue) activation that elicits 40 Hz MN9 firing, as well as bitter GRN (red) or Ir94e GRN activation (purple) activated to reduce 40 Hz MN9 firing to 1 Hz.

We next examined the predicted circuit activity caused by GRNs labelled by the ionotropic receptor Ir94e; these neurons have been identified previously in the electron microscopy volume²³. Ir94e neurons respond to low salt concentrations and the presentation of male genitals, among other substances^31,38, and are suggested to play a role in mediating attraction to low salt³¹. However, the role they play in proboscis extension has not been described. Notably, the computational model predicted that activation of Ir94e GRNs, rather than promoting MN9 firing, inhibits MN9 firing (Fig. 3c). Therefore, we tested whether optogenetic activation of Ir94e GRNs is sufficient to inhibit proboscis extension, similar to bitter activation. Indeed, we found that optogenetic activation of Ir94e GRNs or bitter GRNs was sufficient to inhibit the proboscis extension to 50 mM sucrose, as our modelling predicted (Fig. 3d,e). Interestingly, we noted a quantitative difference between the model’s predictions for bitter versus Ir94e activation. Strong bitter activation is predicted to eliminate MN9 firing to strong sugar stimulation, but strong activation of Ir94e neurons is not predicted to do so (Fig. 3b,c). We therefore tested the proboscis extension response (PER) to 1 M sucrose while optogenetically activating bitter or Ir94e GRNs. Optogenetic bitter activation eliminated consumption of 1 M sucrose (Fig. 3d), but Ir94e activation did not (Fig. 3e). Thus, we conclude that Ir94e GRN activity inhibits proboscis extension, but fails to fully inhibit proboscis extension to strong sugar stimuli. These results indicate that our computational model can predict previously unknown circuit functions and properties.

Finally, we sought to predict how water taste detection influences feeding initiation. The degree to which sugar GRNs and water GRNs activate pathways that are distinct or shared is unknown. We found that activation of water GRNs in our model activates many downstream neurons that are also activated by sugar stimulation. (Fig. 3f, Fig. 4a and Supplementary Tables 1 and 6). In particular, comparing neurons activated by sugar GRNs with those activated by water GRNs, at a stimulation frequency at which each pathway activates MN9 at 40 Hz, predicted that the sugar pathway activates 377 neurons, while the water pathway activates 391 neurons. Of these, more than half (250), are shared between the two circuits (Fig. 3f and Supplementary Table 4). We also examined bitter responsive neurons and Ir94e responsive neurons at the minimal activation sufficient to reduce 40 Hz MN9 firing to 1 Hz. Only two neurons were common between sugar and bitter activation, and 30 between sugar and Ir94e activation, demonstrating segregation of neurons activated by aversive and appetitive taste (Fig. 3f). This prediction is consistent with our previous calcium imaging experiments demonstrating that, across nine sugar-responsive cell types, zero respond to a mixture of bitter compounds⁴. In contrast, our model predicts central neurons that respond to both sugar and water taste activation, as well as sugar-specific and water-specific neurons, consistent with brainwide calcium imaging studies^29,46.

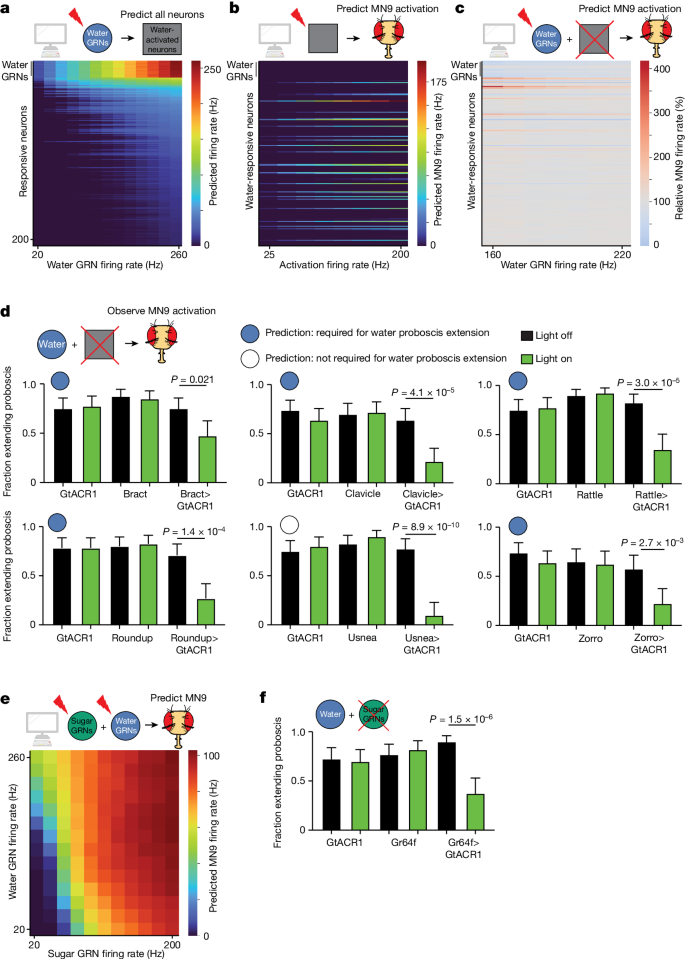
a, Heatmap depicting the predicting firing rates in response to 20 to 260 Hz water GRN firing. The y axis is ordered by firing rate at 260 Hz water activation. b, Heatmap depicting the predicted MN9 firing rate when the top 200 responsive neurons are activated at 25–200 Hz. c, Heatmap depicting the change in MN9 firing rate in response to activation of water GRNs at the specified firing rate, while individually silencing each of the top 200 responsive neurons. d, The fraction of flies exhibiting PER upon water stimulation. Green bars indicate green light condition; n = 30–50; see Supplementary Table 9 for exact values. Open and filled circles represent whether the computational model predicted a greater than 20% decrease in MN9 firing at 160 Hz water GRN stimulation. e, Heatmap depicting the predicted MN9 firing rates in response to the combination of sugar and water GRN activity. f, The fraction of flies exhibiting PER upon water stimulation. n = 39–40. d,f, Mean ± 95% confidence intervals, Fisher’s exact test.

To identify interneurons that compose the water feeding initiation circuit, we used the computational model to analyze the water-responsive neurons that influence MN9 activity. We stimulated the top 200 neurons that are predicted to respond to water, and identified the subset that computationally activates MN9 (Fig. 4b). Next, we also computationally activated water-sensing GRNs, silenced each water-responsive neuron, and monitored the change in MN9 activity (Fig. 4c and Extended Data Fig. 2d). Using our computational model, we identified 39 water-responsive neurons that are also sufficient for MN9 activation. Of these 39, 30 are also predicted to be activated by sugar GRNs (Extended Data Fig. 2d). Furthermore, we identify nine neurons predicted to be both necessary and sufficient for water feeding initiation (Extended Data Fig. 2e). As with sugar, we defined a neuron predicted to be required for water feeding initiation as any neuron that, when silenced, caused MN9 firing to be less than 80% of that of the unsilenced control.

To test these predictions experimentally, we performed calcium imaging on two neurons predicted to respond to water: Fudog and Zorro. We found that both neurons indeed responded to water (Extended Data Figs. 1c and  3a). Additionally, we examined six neurons predicted to have water silencing phenotypes. Five of these, when silenced optogenetically, indeed decreased significantly proboscis extension to water, while a sixth, G2N-1, did not (Fig. 4d and Extended Data Fig. 3b,c). We also examined five neurons that respond to computational water activation, but are not predicted to cause a water silencing phenotype. Of these five neurons, four did not have a water silencing phenotype, as predicted, although one, Usnea, did decrease proboscis extension significantly when silenced with GtACR1 (Fig. 4d and Extended Data Fig. 3b,c).

Our computational model predicts that the water and sugar pathways share a common set of neurons (Extended Data Fig. 2d,e). Do these shared neurons contribute to feeding initiation? Our calcium imaging experiments (Extended Data Figs. 1c and 3a) combined with previous experiments⁴ confirm that five neurons predicted to respond to sugar and water do respond to both sugar and water in vivo: Clavicle, Fudog, Phantom, Rattle and Zorro. Moreover, four of these neurons had been shown previously to be sufficient for proboscis extension, and three are also required for sugar feeding initiation⁴. All three are among the neurons we found experimentally to be required for feeding initiation to water, as predicted (Fig. 4d). Furthermore, the two other cell types we found experimentally to be required for water—Bract and Roundup—are also predicted to respond to both water and sugar (Supplementary Tables 1 and 6), and have been found to respond to sugar⁴. However, previous calcium imaging studies did not identify water responses in these two cell types⁴. This discrepancy may reflect the greater sensitivity of the behavioural silencing experiments compared with calcium imaging of water responses⁴. Finally, a further cell type, Usnea, has been shown to respond to water, but not sugar⁴; our model correctly predicts Usnea responds to water, but incorrectly predicts that it will also respond to sugar. Usnea has previously been shown to be required for feeding initiation to sugar, and our Amontillado RNAi experiments indicate that it may be neuropeptidergic. We find that it is also required for proboscis extension to water (Fig. 4d). Usnea synapses directly onto both sugar and water GRNs (Extended Data Fig. 1b), and may tune the response of these neurons. Thus, we identify a set of neurons involved in the processing of both sugar and water.

To explore the relationship between the water and sugar pathways, we computationally activated both sugar and water GRNs simultaneously and examined the effect on MN9. Our computational modelling predicts that activation of water and sugar GRNs work synergistically to promote MN9 firing (Fig. 4e and Extended Data Fig. 3d). If sugar and water do act synergistically, then both sugar GRNs and water GRNs may be involved in water consumption. Only water GRNs have been implicated in proboscis extension to water; we asked whether sugar GRNs might also be required. Indeed, silencing of sugar GRNs reduced the fraction of flies that extended their proboscis to water (Fig. 4f and Extended Data Fig. 3e). Further, silencing water-sensing neurons reduced consumption of 50 mM sucrose, although a confound is that these water-sensing neurons are known to respond to this concentration of sucrose (Extended Data Fig. 3f). In total, our computational modelling, optogenetic behaviour experiments and functional imaging indicate that the water and sugar pathways share, at least in part, common components to form an appetitive consumption pathway.

To test the general applicability of the computational model to study sensorimotor processing, we sought to determine whether it could predict circuit properties in another system—the well-studied antennal grooming circuit^6,7,8,9,10. In this system, activation of a set of mechanosensory neurons in the Johnston’s organ—a chordotonal organ in the antennae—elicits grooming of the antennae^8,47 (Fig. 5a). These mechanosensory neurons, abbreviated JONs, synapse onto two interneuron types, named antennal grooming brain interneurons 1 and 2 (aBN1 and aBN2), which in turn synapse onto two descending neurons, aDN1 and aDN2 (ref. ⁸). There is a single aBN1 per hemisphere, while there are several aBN2 neurons per hemisphere. Each of these cell types—aBN1, aBN2, aDN1 and aDN2—are sufficient for antennal grooming, while aBN1 and aBN2 are each at least partially required for antennal grooming⁸.

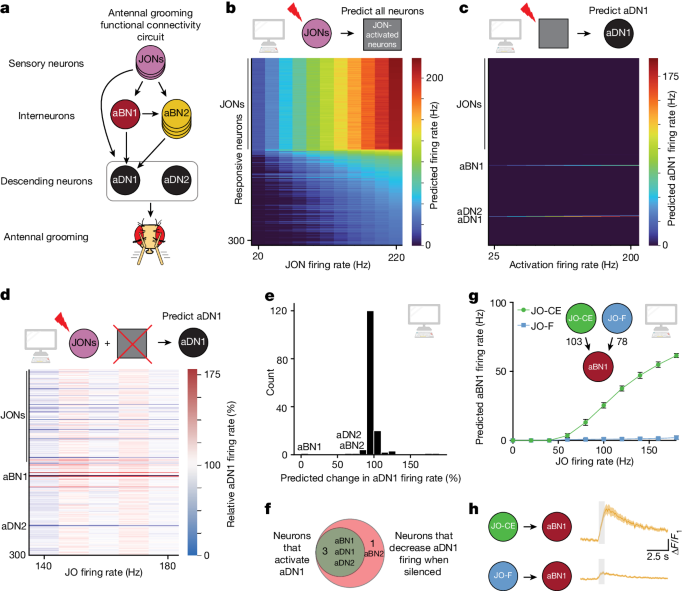
a, Schematic of the antennal grooming circuit. Arrows represent known functional connectivity⁸. Grey oval around aDNs indicates that JONs activate aDNs, but exactly which aDNs are not known. b, Heatmap depicting the predicting firing rates in response to 20–220 Hz JON firing; 147 JONs were activated, and are the neurons that have the highest firing rates. Neurons are ordered by firing rate at 220 Hz. c, Heatmap depicting the predicted aDN1 firing rate when the top 300 responsive neurons are activated at 25–200 Hz. d, Heatmap depicting the change in aDN1 firing rate in response to activation of JOs at the specified firing rate, while individually silencing each of the top responsive neurons. e, Histogram of the predicted change in aDN1 firing rate as a result of silencing each non-JONs, when JONs are activated at 140 Hz. The y axis depicts the number of neurons in each bin. Neurons previously identified are labelled. f, Venn diagram depicting the overlap between neurons predicted to be sufficient to activate aDN1 at greater than 2 Hz and neurons required for aDN1 activation. g, JO subtype connectivity onto aBN1 and predicted aBN1 firing in response to JO activation at the specified rate. Error bars, s.d. h, Calcium imaging of aBN1 in response to optogenetic activation of each subtype. The ΔF/F average ± s.e.m. is shown; n ≥ 5 flies tested. Shaded bar indicates when a red light pulse was delivered.

We first sought to test whether the computational model could identify the previously described neurons in the circuit. We activated a set of 147 previously identified JONs of the JO-C, JO-E, JO-F and JO-m subclasses^8,47. Indeed, the model identified that aBN1, aBN2, aDN1 and aDN2 respond to JON activation (Fig. 5b and Supplementary Table 5). To determine which of these JON-responsive neurons might drive antennal grooming, we computationally activated these neurons and asked whether they could elicit activity in either of the two descending neurons that evoke antennal grooming: aDN1 or aDN2 (Fig. 5c and Extended Data Fig. 4a). Next, we asked, among the top neurons predicted to respond to JON activation, which are required for activation of aDN1 or aDN2 (Fig. 5d and Extended Data Fig. 4b). Notably, only four neurons, beyond aDN1 itself, were identified that could elicit aDN1 activity: aBN1, aDN2 and two other neurons that elicited less than 2 Hz aDN1 activity (Fig. 5c and Supplementary Table 7). Moreover, only three neurons, besides aDN1 itself, were identified that reduced aDN1 activity by more than 20% at 140 Hz JON activation: aBN1; a descending member of the BN2 class; and aDN2 (Fig. 5d–f). Thus, the computational model identifies members of each of the previously identified critical nodes of the antennal grooming circuit purely from knowledge of the sensory inputs and descending outputs.

We next tested how different JON subpopulations influence antennal grooming. JONs send their projections to the antennal mechanosensory and motor center in the ventral brain. JO-C and JO-E neurons respond to antennal vibrations and project medially into the antennal mechanosensory and motor center, while JO-F neurons project into a distinct region⁸. Optogenetic activation of both JO-CE and JO-F neurons is sufficient to trigger antennal grooming, but it is not known whether these two populations generate distinct patterns of downstream firing. Both JO-CE and JO-F neurons synapse onto aBN1 (103 and 78 synapses, respectively; Fig. 5g), raising the possibility that they elicit grooming by activating aBN1.

Our computational model predicts that, whereas JO-CE neurons will elicit robust aBN1 activity, JO-F neurons will not, despite synapsing directly onto aBN1 (Fig. 5g). To test this prediction, we optogenetically activated each population of JONs and performed calcium imaging in aBN1. Consistent with the prediction of this model, JO-CE activated aBN1 robustly, but JO-F neurons did not (Fig. 5h). Why do JO-F neurons fail to activate aBN1 robustly? We identified three putative inhibitory neurons that are directly postsynaptic to JO-F neurons and synapse directly onto aBN1. Computational silencing of these three neurons permits JO-F neurons to activate aBN1, but this remains to be tested empirically (Extended Data Fig. 4c,d). Our analysis of the antennal grooming circuit demonstrates that our computational model can provide insights into complex circuits, purely from knowledge of sensory input and descending output. We demonstrate that modelling brain circuits purely from connectivity and neurotransmitter identity is sufficient to reliably describe, at least at a coarse level, entire sensorimotor transformations.

In conclusion, we report a computational model on the basis of connectivity and neurotransmitter predictions of the entire fly connectome that can predict circuit neural activity, the neurons required for activation of output neurons and the integration of several sensory modalities. We use the model to create predictions of the sugar, water, bitter and Ir94e pathways and validate many of these predictions experimentally. We show that the Ir94e neurons, previously considered to be attractive, instead inhibit proboscis extension. The results of our modelling indicate that sugar, bitter and Ir94e GRNs activate generally distinct populations of neurons. In contrast, sugar and water GRNs activate many of the same central neurons as well as sugar-specific and water-specific neurons. In addition, we recapitulate the antennal grooming circuit purely from sensory input and descending output, and identify a subpopulation of JONs that, despite strong connectivity onto aBN1, fail to activate it. These studies demonstrate the power of computational modelling to explain sensory processing features in complex networks.

Our analysis of the taste and antennal grooming circuits shows we can model local sensorimotor transformations in the taste and antennal grooming circuits. The computational model, implemented in the widely used Brian2 library²², allows for perturbations that are easily interpreted. We believe our computational model will be a useful tool for the study of sensorimotor transformations and the exploration of interactions between overlapping neural pathways (for example, sweet-bitter, sweet-water and so on).