A cellular basis for mapping behavioural structure

Mice

Experiments used adult male C57BL/6 J mice (n = 13; Charles River Laboratories). Mice were housed in a dedicated housing facility on a 12 h light/dark cycle (07:00–19:00) at 20–24 °C and humidity of 55 ± 10%. Mouse experiments were run with four cohorts: two cohorts of four, one cohort of three and one cohort of two, and preselected on the basis of criteria outlined in ‘Behavioural training’ below. No statistical methods were used to pre-determine sample sizes but our sample sizes are similar to those reported in previous publications (for example, in ref. ¹²). Mice were housed with their littermates up until the start of the experiment with free access to water. Food was available ad libitum throughout the experiments, and water was available ad libitum before the experiments. Mice were 2–5 months old at the time of testing. Experiments were carried out in accordance with Oxford University animal use guidelines and performed under UK Home Office Project Licence P6F11BC25.

Behavioural training

The ABCD task

A set of tasks where subjects must find a sequence of 4 reward locations (termed a, b, c and d) in a 3 × 3 grid maze that repeat in a loop. The reward at each location only became available after the previous goal was visited, so the goals had to be visited in sequence to obtain rewards. Once the animal receives reward a the next available reward is in location b (and so on), then once the animal receives reward in location d then reward a becomes available again, creating a repeating loop. An extension of this is the ABCDE task, in which five rewards are arranged in a loop. A brief tone was played upon reward delivery in location a (start of state A), marking the beginning of a loop on every trial. This created an equivalence across tasks for the a location, beyond a single trial memory of the first rewarded location.

Location

When the animal is in the physical maze, it could be at a node (one of the circular platforms where reward could be delivered, coded 1–9 as shown in Fig. 1a), or it could be at an edge, which is a bridge between nodes. The nine maze locations were connected as shown in the top right photograph and adjacent schematic in Fig. 1a, with connections only along the cardinal directions. In our particular maze, edges were only arranged along the cardinal direction, so for example, location 1 was only connected to locations 2 and 4 (Fig. 1a, top right).

Task

An example of the ABCD loop with a particular sequence of reward locations (for example, 1–9–5–7; reward a is in location 1; reward b in location 9, and so on; Fig. 1a).

Session

An uninterrupted block of trials of the same task. We used 20-min sessions. Note that subjects could be exposed to two or more sessions of the same task on a given day. Animals were allowed to complete as many trials as they could in those 20 min. Animals were removed from the maze at the end of a session and either placed back in their home-cage or into a separate enclosed rest/sleep box.

Trial

A single run through an entire ABCD loop for a particular task, starting with reward in location a and ending in the next time the animal gets reward in location a again (for example, trial 12 of a task with the following configuration: 1–9–5–7 starts with the 12th time the animal gets reward in location 1 and ends with the 13th time animal gets reward in location 1).

State

The time period between an animal receiving reward in a particular location and receiving reward in the next rewarded location. State A starts when animal receives reward a and ends when animal receives reward b; state D starts when animal gets reward d and ends when animal gets reward a, and so on.

Transition

A generalized definition of state. For example, progressing from a to b is a transition, and progression from c to d is also a transition.

Goal progress

How much progress an animal has made between rewarded locations as a percentage of the time taken between them. Unless otherwise stated, we operationally divide this into early, intermediate and late goal progress, which correspond to one-third increments of the time taken to get from one reward location to the next. For example, if the animal takes 9 s between one reward and another, then early goal progress spans the first 3 s, intermediate goal progress spans the next 3 s and late goal progress spans the last 3 s. This would scale with the length of time it takes for the animal to complete a single state: for example, if it takes 15 s between two rewards, each of the goal-progress bins would be 5 s long. In the ABCD task, goal progress repeats four times because there are four rewards (so there will be an early goal progress for reward a, and early goal progress for reward b, and so on).

Choice

We use this to refer to one-step choices in the maze. At every node in the maze the animal has a choice of two or more immediately adjacent nodes to visit next. For example, when in node 1 the animal could choose to move to node 2 or node 4 (Fig. 1a).

Apparatus

Maze dimensions: 45 × 45 × 30 cm (length × width × height). Outer dimensions of maze: 66 × 66 × 125 cm. Outer maze walls: instead of solid walls we used electromagnetic field shielding curtains (Electro Smog Shielding (product number: 4260103664431)) that were custom cut to cover the entire outside of the maze. Node dimensions: 11 × 11 cm. Bridge length: 7 cm. Water reservoir height (from bottom of syringe to floor): 80–85 cm. Reservoir filled to 30 ml. Details of the design and material of all maze components are available at https://github.com/pyControl/hardware/tree/master/GridMaze.

Pre-selection

A total of 13 mice across 4 cohorts were used for experiments. For each cohort, 3–4 mice were pre-selected for the experiment from 10–20 mice based on the following criteria:

1. (1)

   Weight above 22 g.

2. (2)

   No visible signs of stress upon first exposure to the maze in the absence of rewards. Stress was evidenced by thigmotaxis or defecation in a 20 min exploration session with no rewards delivered.

3. (3)

   On a partially connected version of the maze with only 5–7 accessible nodes out of 9, animals learned that poking in wells delivered water reward and that after gaining reward they must go to another node. The number of nodes was fixed for a given session. Animals that obtained 40 or more rewards per 20 min session were taken forward to pretraining. The available nodes were connected pseudo-randomly (Extended Data Fig. 1a), such that animals could access all available nodes but there were always “dead-ends”. The identity, number and connectivity of the available nodes was changed for every new 20 min session, to minimize any behavioural biases induced by the exact spatial structure of the maze.

1. (4)

   Final selection: for a given cohort, if more than four animals satisfied these criteria, animals that explored the maze with the highest entropy were selected (see ‘Behavioural scoring’ for entropy calculation).

Habituation and pre-training

After at least one week of post-surgery recovery (see ‘Surgeries’), animals were placed on water restriction. Animals were maintained at a weight of 88–92% of their baseline weight, which was calculated before water restriction but after implantation and recovery from the surgery (see ‘Surgeries’). This is to ensure that they remained motivated to collect water rewards during the task but not overly so, as excessive motivation is known to negatively affect model-based performance⁵⁸. Animals were habituated to being tethered to the electrophysiological recording wire while moving on the maze, as well as in sleep boxes for at least three days prior to the start of the experiment. During this period, animals were reintroduced to a partially connected maze (only 5–7 out of the 9 nodes available, and not all connected) while tethered to the electrophysiology wire, where water reward was delivered if the animal poked its nose at any node. Reward drops were only available once the animal poked its nose at the node. At this stage, there was no explicit task structure, except that once reward was obtained at one node, animals had to visit a different node to gain further reward (that is, exactly as in step 3 of pre-selection criteria above but while implanted and tethered). Thus, animals (re)learned that poking in wells delivered reward and that after gaining reward they must go to another node. Animals were transitioned to the task when they obtained >40 rewards in a 20-min session. Note that 3 animals (from cohort 1) were not implanted and so for these the rewarded sessions for pre-selection and pre-training were one and the same (see ‘Numbers’ for more details on mouse cohorts). The volume of water delivered during pretraining or preselection was higher than training, typically 10–15 µl.

Overall, animals received as few as 2 × 20 min sessions in this partially connected maze where reward is presented in all available nodes and a maximum of 8 × 20 min sessions in total across pre-selection and pre-training. All of these sessions had different configurations connecting the available nodes.

Training

Animals navigated an automated 3 × 3 grid maze in search of rewards (Fig. 1a), controlled using pyControl⁵⁹. Water rewards (3–4 µl) were presented sequentially at 4 different locations. Animals had to poke in a given reward node, breaking an infrared beam that triggered the release of the reward drop in this well. After reward a was delivered, reward was obtainable from location b, but only after the animal poked in the new location. Once the animal received reward in locations a, then b, then c and then d, reward a becomes available again, thus creating a repeating loop. Animals have 20 min to collect as many rewards as possible and no time outs are given if they make any mistakes. They are then allowed at least a 20-min break away from the maze (in the absence of any water) before starting a new session. For each session, animals were randomly entered from a different side of the square maze, using custom-made electromagnetic field shielding curtains (Electro Smog Shielding (product number: 4260103664431)). This was to ensure that all sides of the maze are equivalent in terms of being entry and exit points from the maze, thereby minimizing any place preference/aversion and minimizing the use of different sides as orienting cues. One cue card was placed high up (at least 50 cm vertically from the maze) on one corner of the maze to serve as an orienting cue. No cues were visible at head level.

While all locations were rewarded identically, a brief pure tone (2 s at 5 kHz) was delivered when the animal consumed reward a. This ensured that task states were comparable across different task sequences. White noise was present throughout the session to avoid distraction from outside noises.

Task configurations (the sequence of reward locations) were selected pseudo-randomly for each mouse, while satisfying the following criteria:

1. (1)

   The distance between rewarded locations in physical space (number of steps between rewarded locations) and task space (number of task states between rewarded locations) were orthogonal for each mouse (Extended Data Fig. 1b).

2. (2)

   The task cannot be solved (75% performance or more) by moving in a clockwise or anti-clockwise circle around the maze.

3. (3)

   The first two tasks have location 5 (the middle location) rewarded—this is to ensure the first tasks the animals are exposed to cannot be completed by circling around the outside n times to collect all rewards. (Note that all late tasks and those used in electrophysiological recordings are not affected by this criterion).

4. (4)

   Consecutive tasks do not share a transition (that is, two or more consecutively rewarded locations)

5. (5)

   Chance levels are the same for all task transitions (ab, bc, cd and da), and control transitions ca and ba transitions—whether determined analytically by assuming animals diffuse around the maze or empirically by using animal-specific maze-transition statistics from an exploration session before any rewards were delivered on the maze (see ‘Behavioural scoring’ below for chance level calculations).

For the first 10 tasks, animals were moved to a new task when their performance reached 70% (that is, took one of the shortest spatial paths between rewards for at least 70% of all transitions) on 10 or more consecutive trials or if they plateaued in performance for 200 or more trials. For these first ten tasks, animals were given at most four sessions per day, either all of the same task or, when animals reached criteria, two sessions of the old task and two sessions of the new task. From task 11 onwards, animals learned 3 new tasks a day with the first task being repeated again at the end of each day giving a total of 4 sessions with the pattern X–Y–Z–X′.

To test the behavioural effect of the tone on performance, for cohort 3, 3 mice were additionally exposed to ABCD tasks where the tone was randomly omitted from the start of state A on 50% of trials (the tone was always sounded on the very first A of the session).

To further test the generality of the neuronal representations we uncover here, the fourth cohort (2 mice) experienced ABCDE tasks. This was done after the mice completed all 40 ABCD tasks. On the first day, the mice were exposed to 2 new ABCD tasks, followed by a series of different ABCDE tasks (11 for one mouse and 13 for another) spanning 4 recording days. As before, animals experienced three to four sessions each day.

We tested whether tasks for a given mouse are correlated. For these cross-task correlations, we not only compared sequences with each other, but also with shifted versions of each other to ensure we exhaustively capture any similarities in task sequences. Correlations between tasks with all possible shifts relative to each other were made for a given mouse and then an average correlation value was reported in Extended Data Fig. 1d. Furthermore, the tasks are selected such that no two tasks experienced by the same animal are rotations of each other in physical space.

The sequences of tasks that the animals experienced throughout the experiment were randomized and counterbalanced. Only one experimental group (silicon probe implant in the frontal cortex) was used in this study and so blinding was not necessary.

Surgeries

Subjects were taken off water restriction 48 h before surgery and then anaesthetized with isoflurane (3% induction, 0.5–1% maintenance), treated with buprenorphine (0.1 mg kg^−1) and meloxicam (5 mg kg^−1) and placed in a stereotactic frame. A silicon probe mounted on a microdrive (Ronal Tool) and encased in a custom-made recoverable enclosure (ProtoLabs) was implanted into mFC (anterior–posterior (AP): 2.00, medial–lateral (ML): −0.4, dorsal–ventral (DV): −1.0), and a ground screw was implanted above the cerebellum. AP and ML coordinates are relative to bregma, whereas DV coordinates are relative to the brain surface. Mice were given additional doses of meloxicam each day for 3 days after surgery and were monitored carefully for 7 days after surgery and then placed back on water restriction 24 h before pretraining. At the end of the experiment, animals were perfused; and the brains were fixed-sliced and imaged to identify probe locations (Extended Data Fig. 2a). We used the software HERBS⁵⁷ (version 0.2.8) to localize the probes to anatomical locations on the mouse brain based on the histology images (Fig. 2a and Extended Data Fig. 2b). For the neuropixels recordings, this was done directly by finding the entire probe track. For Cambridge neurotech probes, we found the top entry point of each of the 6 shanks and the bottom was inferred based on the final DV position reached by the probe post-surgery and nanodrive-based lowering. This was marked for each mouse in Fig. 2a and Extended Data Fig. 2b and matched to a standardized template to deduce anatomical regions corresponding to the probe positions.

Using this method, we found that 90.7% of all recorded neurons were histologically localized in mFC regions: 68.3% in Prelimbic cortex, 11.3% in anterior cingulate cortex, 6.1% in infralimbic cortex and 5.0% in M2. Of the remaining 9.3%, 4.8% could not be localized to a specific peri-mFC region within the atlas coordinates as they were erroneously localized to peri-mFC white matter areas, likely due to variations between actual region boundaries and those derived from the standard template provided by the HERBs software, 2.2% were found in the dorsal peduncular nucleus, 1.1% in the striatum, 0.6% in the medial orbital cortex, 0.3% in the lateral septal nucleus and 0.3% in olfactory cortex. We used all recorded neurons in the analyses throughout the manuscript but indicate where these pertain to different mFC regions in Extended Data Figs. 2i, 4j,k and 7f.

Electrophysiology, spike sorting and behavioural tracking

Cambridge NeuroTech F-series 64 silicon channel probes (6 shanks spanning 1 mm arranged front-to-back along the anterior–posterior axis) were used for 3 of the 4 cohorts (5 mice). To record from the mFC, we lowered the probe ~100 µm during the pre-habituation period to reach a final DV position of between −1.3 and −1.5 mm below the brain surface (that is, between −2.05 and −2.25 mm from bregma). This places most channels in the prelimbic cortex (http://labs.gaidi.ca/mouse-brain-atlas/) (Fig. 2a and Extended Data Fig. 2b). For the fourth cohort (2 mice) we used neuropixels 1.0 probes that were fixed at a DV position of 3.8–4 mm from the brain surface, AP 2.0 mm from bregma and ML −0.4 from bregma. This gave us the ability to record from more regions along the entire medial wall of mFC, including regions such as secondary motor cortex (M2), dorsal and ventral anterior cingulate (ACC), and infralimbic cortex, as well as the prelimbic cortex (Fig. 2a and Extended Data Fig. 2b). Neural activity was acquired at 30 kHz with a 32-channel Intan RHD 2132 amplifier board (Intan Technologies) connected to an OpenEphys acquisition board. Behavioural, video and electrophysiological data were synchronized using sync pulses output from the pyControl system. Recordings were spike sorted using Kilosort⁶⁰, versions 2.5 and 3, and manually curated using phy (https://github.com/kwikteam/phy). Clusters were classified as single units and retained for further analysis if they had a characteristic waveform shape, showed a clear refractory period in their autocorrelation and were stable over time.

To increase the number of tasks assessed for each neuron, we concatenated pairs of days to obtain six tasks. For concatenated double days, we tracked neurons by concatenating all binary files from sessions recorded across two days. A single concatenated binary file with data from two days was run through the standard kilosort pipeline to automatically extract and sort spikes. We manually curate the output of this file based on standard criteria:

1. (1)

   Contamination of a refractory period (2 ms) as determined by a spike autocorrelogram – to be at most 10% of the baseline bin, which is defined as the number of spikes in the 25-ms bin (the maximum value for the autocorrelation plots used for curation in kilosort).

2. (2)

   Neurons where the firing rate in 3 or more sessions drops below 20% of the session with the peak firing rate are discarded.

These criteria result in a total percentage of spikes in 1 ms and 2 ms refractory periods of: 0.033% ± 0.003% and 0.076% ± 0.004% of spikes on average respectively. We also note that 99.2% of neurons have a maximum dropoff of spike counts at 2 ms or more.

Dropout rate: by comparing the units designated ‘good’ by kilosort before curation with the post-curation yield, we find a dropout rate of 51.4% for the concatenated double days. This is in comparison to a dropout rate of 29.7% for single days.

We find that concatenation overwhelmingly succeeds in capturing the same neuron across days. For this we take advantage of the highly conserved goal-progress tuning that is characteristic of mFC neurons (Fig. 2). We assessed ‘goal-progress correlation’ between different tasks that are taken from the same day and then repeated this for the same neuron for pairs of tasks taken from different days. This allowed us to index the extent to which basic tuning of cells is conserved across days (both in ABCD and ABCDE days). This shows:

1. (1)

   An exceptionally tight relationship between each neuron’s within and across-day goal-progress correlation—that is, goal-progress correlation between tasks in the same day is itself highly correlated with goal-progress correlation between tasks across days. Pearson correlation n = 1,540 neurons, r = 0.88, P = 0.0.

2. (2)

   Another way of looking at this: goal-progress correlation values are indistinguishable within and across days—that is, for a given neuron, goal-progress tuning is equally likely to be conserved across days as it is within the same day. (Within-day correlation: 0.63 ± 0.01, across-day correlation: 0.62 ± 0.01 Wilcoxon test: n = 1,549, W-statistic =567,550, P = 0.14, d.f. = 1,540)

3. (3)

   Almost all neurons that are significantly goal-progress-tuned within a day also maintain their goal-progress tuning across days (95.4%; two proportions test: n = 1,249 neurons, z = 45.2, P = 0.0). Significance was calculated by comparing goal-progress correlation to the 95th percentile of circularly shifted permutations, individually for each neuron.

We performed tracking of the mice in the video data using DeepLabCut⁶¹ (version 2.0), a Python package for marker-less pose estimation based in the TensorFlow machine learning library. Positions of the back of a mouse’s head in xy pixel coordinates were converted to region of interest information (which maze node or edge the animal is in for each frame) using a set of binary masks defined in ImageJ that partition the frame into its sub components.

Data analysis

All data were analysed using Python (3) code. This used custom-made code but made use of libraries such as numpy (1.22.0), scipy (1.10.1), matplotlib (3.7.3), sciKit learn (1.3.2), pandas (2.0.3) and seaborn (0.13.2).

Behavioural scoring

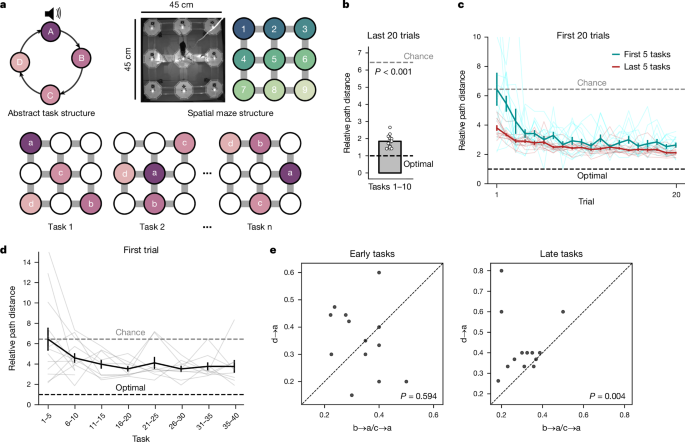
Performance was assessed by quantifying the percentage of transitions (for example, a to b) where animals took one of the shortest available routes (for example, Extended Data Fig. 1j), or percentage of entire trials where animals took the shortest possible path across all transitions (Extended Data Fig. 1k). We also quantified the path length taken between rewards and divided this by the shortest length to give the relative path distance covered per trial (for example, Extended Data Fig. 1i).

When using percentage of shortest path transitions as a criterion, chance levels were calculated either analytically or empirically. Analytical chance levels were calculated by assuming a randomly diffusing animal and calculating the chances the animal will move from node X to node Y in N steps. This is used in Extended Data Fig. 1o to ensure that the comparison of DA with BA/CA for zero-shot quantification is a fair one. Empirical chance levels were calculated by using the location-to-location transition matrix recorded for each animal in the exploration session before any exposure to reward on the maze. Empirical chance is calculated in two different places:

1. (1)

   When finding the probability of a shortest-path transition. Pre-task exploration chance levels are calculated by quantifying each animal’s transition probabilities around the maze in an exploration session prior to seeing any ABCD task (or any reward on the maze). This is used in Extended Data Fig. 1n, again to ensure that the DA to BA/CA comparison for zero-shot quantification is a fair one.

2. (2)

   When setting a chance level for the relative path distance measure. Chance here is defined as the mean relative path distance for transitions in the first trial averaged across the first five tasks across all animals. This is used in Fig. 1b–d.

Correct transition entropy (the animal’s entropy when taking the shortest route between rewards) was calculated for transitions where there was more than one shortest route between rewards. We calculated the probability distribution across all possible shortest paths for a given transition and calculated entropy as follows:

Where x is the logarithmic base, which is set to the number of shortest routes, and pk is the probability of each transition. Thus an entropy of 1 signifies complete absence of a bias for taking any one path and an entropy of 0 means only one of the paths is taken (that is, maximum stereotypy).

To quantify the effect of pre-configured biases in maze exploration on ABCD task performance in Extended Data Fig. 1h we analyse the per mouse correlation between:

1. 1.

   Relative path distance on a given trial in an ABCD task—that is, ratio of taken path distance versus optimal (shortest) path distance.

2. 2.

   The mean baseline probability for all steps actually taken by the animal on that same trial (measured from an exploration session before exposure to any ABCD task)—that is, how likely was the animal to take this path on a given trial before task exposure?

This correlation is positive overall, indicating that when animals take more suboptimal (longer) routes they do so through high probability steps—that is, ones that they were predisposed to take prior to any task exposure. This suggests that mistakes are associated with persisting behavioural biases.

Activity normalization

We aimed to define a task space upon which to project the activity of the neurons. To achieve this, we aligned and normalized vectors representing neuronal activity and maze location to the task states. Activity was aligned such that the consumption of reward a formed the beginning of each row (trial) and consumption of the next reward a started a new row. Normalization was achieved such that all states were represented by the same number of bins (90) regardless of the time taken in each state. Thus, the first 90 bins in each row represented the time between rewards a and b, the second between b and c, the third between c and d and the last between d and a. We then computed the averaged neuronal activity for each bin. Thus the activity of each neuron was represented by an n × 360 matrix, where n is the number of trials and 360 bins represent task space for each trial. This activity was then averaged by taking the mean across trials, and smoothed by fitting a Gaussian kernel (sigma = 10°). To avoid edge effects when smoothing, the mean array was concatenated to itself three times, then smoothed, then the middle third extracted to represent the smoothed array. To reflect the circular structure of the task, the mean and standard error of the mean of this normalized and smoothed activity were projected on polar plots (for example, Fig. 2c,d).

Generalized linear model

To assess the degree to which mFC neurons are tuned to task space, we used a linear regression to model each neuron’s activity and permutation tests to determine significance¹⁸. Specifically, we aimed to quantify the degree to which goal-progress and location tuning of the neurons is consistent across tasks and states. For this we used a leave-one-out cross-validation design: we divided all tasks into the time periods spanned by each of the four states and used all data except one task–state combination to train the model. The remaining task–state combination (for example, task 3, state B) was used to test the model. This was repeated so that each task–state combination had been left out as a test period once. The training periods were used to calculate mean firing rates for five levels of goal progress relative to reward (five goal-progress bins) and each maze location (nine possible node locations). Edges were excluded from analyses since they are systematically not visited at the earliest goal-progress bin. The mean firing rates for goal progress and place from the training task-state combinations were used as (separate) regressors to test against the binned firing rate of the cell in the test data (held out task-state combination). We note that this procedure gives only one regressor for each variable, where the regressor takes a value equal to the mean firing rate of the cell in a given bin for the variable in question in the training data. For example, if a neuron fired at a mean rate of 0.5 Hz in location 6 in the training data, then whenever the animal is in location 6 in the test data the regressor for ‘place’ takes a value of 0.5. In effect, this analysis asks whether the tuning of a given neuron to a variable is consistent across different task–state combinations. To assess the validity of any putative task tuning, a number of potentially confounding variables were added to the model. These were: acceleration, speed, time from reward, and distance from reward. This procedure was repeated for all task–state combinations and a separate regression coefficient value was calculated for each.

To assess significance a given neuron was tuned to a given variable, we required it to pass two criteria:

1. (1)

   To have a mean regression coefficient higher than a null distribution: the null distribution is derived from repeating the regression but with random circular shifts of each neuron’s activity array and computing regression coefficient values for each iteration (100 iterations) and then using the 95th percentile of this distribution as the regression coefficient threshold.

2. (2)

   To have a cross-task correlation coefficient significantly higher than 0: activity maps were computed for place (a vector of 9 values corresponding to 9 node locations) or goal progress (a vector of 5 values corresponding to 5 goal-progress bins) and then Pearson correlations calculated between each pairwise combinations of unique tasks. To ensure this analysis is sufficiently powered, we only used data concatenated across two days (giving up to six unique tasks). A two-sided one-sample t-test was then conducted to compare these cross-task correlation coefficients against 0.

Only neurons that passed both tests were considered tuned to a particular variable and reported as such in Fig. 2g and Extended Data Fig. 2e. We note that we do not use this tuning status anywhere else in the manuscript. Where we subset away spatial neurons (for example, Extended Data Figs. 2j,k and 4d,g), we deliberately use a less stringent criteria for spatial tuning to ensure that even neurons with weak or residual spatial tuning are excluded from the analysis (this excludes 76% of neurons), and hence ensure that results are robust to any spatial tuning. Where we subset in state neurons we use different criteria outlined in the section immediately below.

To determine whether the population as a whole was tuned to a given variable, we performed two proportions z-tests to assess whether the proportion of neurons with significant regression coefficient values for a given variable were statistically higher than a chance level of 5%.

To determine whether goal-progress tuning was also robust in ABCDE tasks, we performed the exact same procedure as above for ABCD tasks (Extended Data Fig. 3b). Moreover, to determine whether goal-progress tuning was conserved across tasks with different abstract structure, we performed an additional GLM on the cohort that experienced ABCD and ABCDE tasks. We used a train-test split where ABCDE tasks served as training tasks to determine mean firing rates for different goal-progress bins and for different place bins and then inputted these values to perform the regression in the ABCD tasks which were left out as test tasks. We again added acceleration, speed, time from reward and distance from reward as co-regressors (Extended Data Fig. 3f).

To exclude any neuron with trajectory tuning from the analysis of lagged tuning below we also ran a separate GLM this time replacing place with conjunctions of current place and the next step. This gave a vector of 24 possible place-next-place combinations which were used as regressors in the same manner as with place tuning above. Namely, the mean firing rates for place–next-place combinations from the training task-state combinations were used as regressors to test against the binned firing rate of the cell in the test data (held out task-state combination). This was done while regressing out goal progress, acceleration, speed, time from reward, and distance from reward as above. This procedure was repeated for all task–state combinations and a separate regression coefficient value was calculated for each. The mean regression coefficient was then compared to the 95th percentile of coefficients from permuted data (using circular shifts as above). This was the only criteria used, which meant we were deliberately lenient to ensure that any cells with even weak trajectory tuning were excluded from the analysis in Extended Data Fig. 8c.

State tuning

For state tuning, we first wanted to test whether neurons were tuned to a given state in a given task. We therefore analysed state tuning separately from the GLM above, which explicitly tests for the consistency of tuning across tasks. Instead, we used a z-scoring approach. First we took the peak firing rate in each state and trial, giving 4 values per trial: that is, a maximum activity matrix with dimensions n × 4, where n is the number of trials. Then we z-scored each row of this maximum activity matrix (that is, giving a mean of 0 and standard deviation of 1 for each trial). We then extracted the z-scores for the preferred state across all n trials and subsequently conducted a t-test (two-sided) of this array against 0. Neurons with a P value of <0.05 for a given task were taken to be state-tuned in that task. We also used a more stringent P value of <0.01 to assess whether results where we only use a subset of state-tuned neurons are robust even for highly state-tuned neurons. This is used when assessing the degree of generalization and coherence of neurons across tasks (Extended Data Fig. 4b,e: see ‘Neuronal generalization’) and when assessing invariance of cross-task anchoring (Extended Data Fig. 8b: see ‘Lagged task space tuning’ section below).

Manifold analysis

To visualize and further quantify the structure of neuronal activity in individual tasks, we embedded activity into a low dimensional space using UMAP, a non-linear dimensionality reduction technique previously used to visualize mFC population activity^34,49. For this analysis we only used concatenated double days that: (1) had at least 6 tasks; and (2) had at least 10 simultaneously recorded neurons. As input, we used z-scored, averaged, time-normalized activity of each neuron recorded across concatenated double days (see ‘Activity Normalization’) and repeated this for each task. For ABCD tasks, this gave an n x 360 input matrix where n is the number of neuron tasks (each neuron repeated for 6 tasks) and 360 bins represent 4 × 90 bins for each state. This allowed us to assess the manifold structure within (rather than across) tasks. This high-dimensional (n × 360) matrix was then used as an input to the UMAP, with the output being a low-dimensional (3 × 360) embedding. We used parameters (3 output dimensions, cosine similarity as the distance metric, number of neighbours = 50, minimum distance = 0.6) in line with previous studies^34,49.

The output of this was plotted while projecting either a colour map indicating goal-progress (for example, Fig. 2h, left) or task state (for example, Fig. 2h, right) onto the manifold. This showed a hierarchical structure where goal-progress sequences were concatenated into a floral structure that distinguished different states. To quantify this effect we conducted the UMAP analysis separately for each recording (double) day and measured distances in the low dimensional manifold between: (1) bins that have opposite goal-progress bins and different states (across-goal progress); (2) bins that share the same goal-progress bin but represent different states (within-goal progress); and (3) bins that have the same goal-progress bin but where state identity was randomly shuffled across trials to destroy any systematic state-tuning (shuffled). This latter control was used as a floor to test whether distances between states were significantly above chance (which all analyses show that they were). This analysis showed that bins across different states that share the same goal progress were significantly closer than those across opposite goal progress, providing further support for the hierarchical organization of mFC neurons in a single task into state-tuned manifolds composed of goal-progress sequences. To ensure state-discrimination is not due to any spatial tuning, we repeated this analysis for only non-spatial neurons (excluding even weakly spatially tuned neurons; see ‘Generalized linear model ’; Extended Data Fig. 2j,k). We also repeated the same procedure for data from the ABCDE task (Extended Data Fig. 3g,h).

Importantly, these manifolds in Fig. 2 and associated extended data figures pertain to individual tasks. They do not show a manifold that generalizes across tasks. Our findings in Figs. 3 and 5 show that the abstract task structures are not encoded by a single manifold, but rather a number of separate SMBs, each anchored to a different location–goal progress combination. It is not possible to visualize the entire multi-SMB manifold using UMAP or any dimensionality reduction method given that the minimum number of possible anchors (9 locations × at least 3 goal-progress bins = a minimum of a 27-dimensional space) makes the full manifold high-dimensional and hence not amenable to being compressed into a lower number of dimensions. In reality we predict many more modules given the high resolution of goal-progress tuning (Fig. 2c–f) and the fact that spatial anchors are typically multi-peaked, giving a large number of possible spatial pattern combinations and hence many more than 9 possible anchors (for example, Fig. 5g). This forces us to use high dimensional methods like the coherence and clustering analysis in Fig. 3 and the anchoring analysis in Fig. 5 to analyse the SMBs. Another way of stating this is to note that dimensionality reduction techniques are useful when visualizing each time point in the task as a single point in a low-dimensional space. However, we find that each time point in the task is actually represented by multiple points on multiple SMBs, each encoding a lag from a different anchor (Fig. 5). This means we cannot meaningfully plot the full SMB structure using the dimensionality reduction techniques used in the field. A useful comparison point are toroidal manifolds of grid cells in the mEC. Here the torus is only visible when a large number of neurons (>100) are isolated from a single module⁴⁵. We can in principle show a manifold for a single SMB. However, given that we are dealing with orders of magnitude more mFC task modules than mEC grid modules (of which there are typically 6) we need orders of magnitude higher neuronal yields than the best cortical yields currently achievable to obtain 100+ neurons in a single mFC module.

Neuronal generalization

To assess whether individual neurons maintained their state preference across tasks we quantified the angle made between a neuron in one task and the same neuron in another task. Only state-tuned neurons were used in these analyses. To ensure we captured robustly state-tuned neurons, we restricted analyses to neurons state-tuned in more than one-third of the recorded tasks. This subsetting is used throughout the manuscript where state-tuned cells are investigated. Quantifying the angle between neurons was achieved by rotating the neuron in task Y by 10° intervals and then computing the Pearson correlation between this rotated firing rate vector and the mean firing rate vector in task X. Using this approach, we found for each neuron the rotation that gave the highest correlation. For cross-task comparisons we calculated a histogram of the angles across the entire population and averaged this across both comparisons (X versus Y and X versus Z). Within task histograms were computed by comparing task X to task X′ (Fig. 3b). To compute the proportion of neurons that generalized their state tuning, we found the maximum rotation across both comparisons (X versus Y and X versus Z). We then set 45° either side of 0 rotation across all tasks as the generalization threshold (orange shaded region in Fig. 3b). Because this represents one-quarter of the possible rotation angles, chance level is equal to m/4, where m is the number of comparisons. When calculating generalization across one comparison, chance level is therefore 25%, whereas when two comparisons are taken, the chance level is 1/16 (6.25%). This definition of generalization accounts for the strong goal-progress tuning, ensuring that the chance level for this ‘close-to-zero’ proportion is 1/4 for a single task-to-task comparison and 1/16 for 2 task-task comparisons regardless of goal-progress tuning.

Generalization could also be expressed at the level of tuning relationships between neurons. For example, two neurons that are tuned to A and C in one task could then be tuned to B and D in another, thereby maintaining their task-space angle (180°) but remapping in task space across tasks. To test for this, we computed the tuning angle between pairs of neurons and assessed how consistent this was across tasks. This angle was computed by rotating one neuron by 10° intervals and calculating the Pearson correlation between the mean firing vector of neuron k and the rotated firing vector for neuron j. The rotation with the highest Pearson correlation gave the between-neuron angle (Fig. 3c). Thus, we compared the angle between a pair of neurons in task X to the same between-neuron angle in tasks Y and Z. Again histograms were averaged across both comparisons (X versus Y and X versus Z) for cross-task histograms while within-task histograms were computed by comparing task X to task X′ (Fig. 3c). To compute the proportion of neuron pairs that were coherent across tasks, we found the maximum rotation of the angle between each pair across both comparisons (X versus Y and X versus Z). We then set 45° either side of 0 rotation across all tasks as the coherence threshold (orange shaded region in Fig. 3c). Because this represents one-quarter of the possible rotation angles, chance level is equal to m/4, where m is the number of comparisons, and therefore is 25% for one comparison and 1/16 (6.25%) for two comparisons. This definition of coherence accounts for the strong goal-progress tuning, ensuring that the chance level for this ‘close-to-zero’ proportion is 1/4 for a single task-to-task comparison and 1/16 for 2 task-task comparisons regardless of goal-progress tuning.

This method quantifies remapping by finding the best rotation that matches the same neuron across tasks. While this mostly aligns well with the angles seen by visually inspecting the changes in the firing peak, in some cases (for example, Fig. 3a, neuron 3, session X versus Z) there is a discrepancy between the ‘best-rotation’ angle and the ‘peak-to-peak’ angle. This is because the best-rotation measure takes the entire shape of the tuning curve into account. It is therefore robust to small changes in the size of peaks when there is more than one similarly sized peak (for example, neurons 2, 4 and 6 in Extended Data Fig. 4l), which would introduce major inaccuracies in calculating remapping angles when using the peak to measure cross-session changes. Hence our preference for the best-rotation-based approach. However, we note that any ambiguity in calculating angles will introduce unstructured noise that works against us rather than introducing any biases that would induce false coherence. Nevertheless, to make this point robustly, we repeat the single cell generalization and pair-wise coherence analyses while using only state-neurons with concordant remapping angles across both methods (that is, using the best-rotation analysis method and peak-to-peak changes method) for all cross-session comparisons (Extended Data Fig. 4c,f). This would, for example, exclude neuron 3 in Fig. 3a, which on one cross-session comparison rotates differently when using the best rotation versus peak change methods in the X versus Z comparison. We show that the same results hold even under this condition: individual neurons do not generalize but pairs of neurons are partially coherent across tasks Extended Data Fig. 4c,f.

To assess whether the mFC population was organized into modules of coherently rotating neurons, we used a clustering approach. In the trivial case, where all neurons remap randomly, we expect 16 possible clusters. This is because we assess clustering across 3 tasks, which gives two comparisons (X versus Y and X versus Z). For each comparison there are 4 possible ways a given neuron can remap, creating 4 groups (neurons remapping by 0°, 90°, 180° or 270°). In the second comparison, there are another 4 ways the neurons could remap. Thus the number of clusters is 16 (that is, 4²). This assumes remapping is always exactly in 90° intervals—that is, perfect goal-progress tuning. In reality, goal-progress tuning is not perfect and so more clusters are expected in the null condition. To avoid such assumptions, we create a null distribution that preserves the neurons’ state tuning in the first task and goal-progress tuning throughout all tasks, but where each neuron otherwise remaps randomly across tasks. The procedure was as follows:

Step 1: take the maximum difference in pairwise, between-neuron angles across all comparisons and convert this into a maximum circular distance (1 − cos(angle)), thereby generating a distance matrix reflecting coherence relationships between neurons (incoherence matrix).

Step 2: Compute a low dimensional embedding of this incoherence matrix, using t-distributed stochastic neighbour embedding (using the TSNE function of scikit learn manifold library, with perplexity = 5).

Step 3: Use hierarchical clustering on this embedded data (using the AgglomerativeClustering function of scikit learn cluster library, with distance threshold = 300). This procedure sorts neurons into clusters reflecting coherence relationships between neurons. We note that this analysis derives the number of clusters (modules) obtained across three tasks rather than the true number of modules across an arbitrarily large number of tasks.

We quantified the degree of clustering by computing the silhouette score for the clusters computed in each recording day:

Where a = mean within-cluster distance and b = mean between-cluster distance. We repeated the same procedure but for permuted data, where state tuning in task X and goal-progress tuning in all tasks was identical to the real data but the state preference of each neuron remapped randomly across tasks. This allowed us to compare the Silhouette Scores for the real and permuted data (Fig. 3d). To visualize clusters and the tuning of neurons within them in the same plot, we plotted some example neurons from a single recording day where the x and y axes represented state tuning and the y axis arranged neurons based on their cluster ID (the ordering along the z axis is arbitrary; Fig. 3e).

Lagged task space tuning

The task-SMB model predicts the existence of neurons that maintain an invariant task space lag from a particular anchor representing a behavioural step, regardless of the task sequence. Concretely, behavioural steps are conjunctions of goal progress (operationally divided into early, intermediate or late) and place (nodes 1–9). To test this prediction, we used three complementary analysis methods. All of these analyses were conducted on data where two recording days were combined and spike-sorted concomitantly, giving a total of six unique tasks per animal (with two exceptions that had four and five tasks each; see exclusions under ‘Numbers’). For all of these analyses, only state-tuned neurons were used (see ‘State tuning’).

The main reason for using concatenated days is to be sufficiently powered for the generalization analyses (in Fig. 5). In essence the aim is to capture multiple instances where animals visit the same anchor points (for example, same reward locations) but in different sequences. The more tasks we can get for this the more we can sample the same reward locations in different task sequences. With 3 tasks, a total of 12 reward locations are presented (4 × 3) meaning each of the 9 reward locations is seen in 1.33 different tasks on average. With 6 tasks, reward locations are experienced in 2.67 different tasks on average. This gives us the ability to assess the same anchor points in different task sequences in a cross-validated manner and hence assess whether lagged tuning to anchor is conserved across tasks. For example, a neuron fires 2 states after reward in location 7 regardless of whether the animal is now in location 1 or 8. For non-rewarded locations, the situation is more complex and dependent on the animal’s behavioural trajectories between rewards, but the same qualitative principle applies: more tasks give more visits to a given behavioural step as part of different behavioural sequences.

Method 1: Single anchor alignment. This approach assumes each neuron can only have a single goal-progress/place anchor and quantifies the degree to which task-space lag for this neuron is conserved across tasks. We fitted the anchor by choosing the goal-progress/place conjunction which maximizes the correlation between lag-tuning-curves in all but one (training) tasks, and again used cross-validation by assessing whether this anchor leads to the same lag tuning in the left-out (test) task. The fitting was conducted by first identifying the times an animal visited a given goal-progress/place and sampling 360 bins (1 trial) of data starting at this visit, then averaging activity aligned to all visits in a given task, and smoothing activity as described above (under ‘Activity normalization’). This realigned activity is then compared across tasks to compute the angle (θ) between the neuron’s mean aligned/normalized firing rate vector across tasks. This involves essentially doing all the steps for the ‘Neuronal generalization’ but for the anchor-aligned activity instead of state A-aligned activity. This was done for all possible task combinations and then a distance matrix (M) was computed by taking distance = 1 − cos(θ). This distance matrix M has dimensions N_{training tasks} × N_{training tasks} × N_anchors (typically 5 × 5 × 27 as there are usually 6 tasks, meaning 5 training tasks are used, and 3 × 9 possible anchors corresponding to 3 possible goal-progress bins (early, intermediate and late) and 9 possible maze locations). The distance can then be averaged across all comparisons to find the mean distance between all comparisons for a given anchor for a given training task, generating a mean-distance matrix (M_mean). This M_mean matrix has the dimensions N_comparisons × N_anchors; where N_comparisons = N_{training tasks} − 1; typically this will be 4 × 27. The entry with the minimum value in this N_mean matrix gives the combination of training task and goal-progress/place anchor that best aligns the neuron—the training task selected is used as the reference task to do the comparison below. Next, the neuron’s mean activity in the test task is aligned to visits to the best anchor calculated from the training tasks. This allows calculating how much this aligned activity array has remapped relative to the aligned activity in the reference training task—if it has remapped by 0° or close to 0° (within a 45° span either side of zero) then the neuron is anchored (that is, maintains a consistent angle with its anchor across tasks). For a given test-train split, we computed a histogram of the angles across all the neurons and then we averaged the histograms across all test-train splits to visualize the overall distribution of angles between training and test tasks (for example, Fig. 5b). To quantify the degree of alignment further, we measured the correlation between the anchor-aligned activity of neurons in the test task versus reference training task. Importantly, to account for the strong goal-progress tuning of cells we only consider activity of neurons in their preferred goal-progress bin when calculating this correlation (Fig. 5c). The neuron’s lag from its anchor was identified by finding the lag at which anchor-aligned activity was maximal. This lag is used below for ‘Predicting behavioural choices’.

Method 2: Lagged spatial similarity. To detect putative lagged task space neurons, we calculated spatial tuning to where the animal was at different task lags in the past (Fig. 5e). While spatial neurons should consistently fire at the same locations(s) at zero lag, neurons that track a memory of the goal-progress/place anchor will instead show a peak in their cross-task spatial correlation at a non-zero task lag in the past (Fig. 5e). To quantify this effect, we used a cross-validation approach, using all tasks but one to calculate the lag at which cross-task spatial correlation was maximal, and then measuring the Pearson correlation between the spatial maps in the left-out task and the training tasks at this lag (Fig. 5f). To account for the strong goal-progress tuning of the neurons, all maps were computed in each neuron’s preferred goal progress. We note that it is the firing rates that are calculated in the preferred goal-progress bins of each neuron. The spatial positions are then derived either in the same bin (that is, the ‘present’), or in bins successively further back in the past (making a total of 12 bins spanning the entire 4 states at a resolution of 3 goal-progress bins per state).

Method 3: Model fitting. For each neuron we computed a regression model that described state-tuning activity as a function of all possible combinations of goal-progress/place and all task lags from each possible goal-progress/place. Thus a neuron could fire at a particular goal-progress/place conjunction but also at a particular lag in task space from this goal-progress/place. We used an elastic net (using the ElasticNet function from the scikit learn linear_model package) that included a regularization term which was a 1:1 combination of L1 and L2 norms. The alpha for regularization was set to 0.01. A total of 9 × 3 × 12 (312) regressors were used for each neuron, corresponding to 9 locations, 3 goal-progress bins (so 27 possible goal-progress/place anchor points) and 12 lags in task space from the anchor (4 states × 3 goal-progress bins). We trained the model on five (training) tasks and then used the resultant regression coefficients to predict the activity of the neuron in a left-out (test) task. To ensure our prediction results are due to state preference and not the strong effect of goal-progress preference (Fig. 2), both training and cross-validation were only done in the preferred goal progress of each neuron. For non-zero-lag neurons, we only used state-tuned neurons with all of the three highest regression coefficient values at non-zero lag from an anchor (lag from anchor of 30° or more for Fig. 5h, right; 90° (one state) or more for Extended Data Fig. 8a) in the training tasks. Also, for non-zero lag neurons, we only use regression coefficient values either 30° (Fig. 5h, right) or 90° (Extended Data Fig. 8a) either side of the anchor point to predict the state tuning of the cells. This ensured that the prediction was only due to lagged activity and not direct tuning of the neurons to the goal-progress/place conjunction.

The above analysis models neuronal activity as a linear function of anchor lags. To investigate the robustness of our findings to this assumption, we repeated this analysis using a linear–nonlinear–Poisson model which uses a non-linear (logarithmic) link function. We used a regularization alpha = 1. This type of model has been traditionally used to model neuronal tuning while accounting for non-linearities⁶².

For per mouse effects reported in Extended Data Figs. 7e,i and 8e, we tested whether the number of mice with a mean cross-validated correlation above 0 is higher than chance, chance level being a uniform distribution (50:50 distribution of per mouse correlation means above and below zero). We used a one-sided binomial test against this chance level. All seven mice need to have mean positive values for this test to yield significance.

Predicting behavioural choices

The SMB model proposes that behavioural choices should be predictable from bumps of activity along specific memory buffers long before an animal makes a particular choice. By ‘choice’ here we mean a decision to move from one node to one of the immediately adjacent nodes on the maze (for example, from location 1 should I go to location 2 or 4?; Fig. 6a). To test whether these choices are predictable from distal neuronal activity we used a Logistic regression model. For this analysis we used only consistently anchored neurons, that is neurons that had the same anchor and same lag to anchor in at least half of the tasks. This relied on the single-anchor analysis (Fig. 5a; see ‘Lagged task space tuning’, Method 1: Single anchor alignment) to find for each cell its preferred anchor and lag from anchor. Furthermore, to avoid contamination of our results due to simple spatial tuning, we only used neurons with activity lagged far from their anchor (one third of an entire state—that is, in the ABCD task at least 30° in task space either side of the anchor (for example, Fig. 6c); and this was also repeated for lags of at least 90° (one whole state) either side of the anchor in Extended Data Fig. 9d). For the ABCDE task, the equivalent ‘close-to-zero-lag’ period was 24° (1/3 of one state which is 72°; Extended Data Fig. 9i). We measured the activity of a given neuron during its bump time—that is, the time at which a neuron is lagged relative to its anchor. Precisely, this is the mean firing rate from a period starting with the lag time from the anchor and ending 30° forward in task space from that point (1/3rd of a state). This mean activity was inputted on a trial by trial basis every time the animal was at a goal-progress/place conjunction that was one step before the goal-progress/place anchor in question (for example, if the anchor is at early goal progress in place 2, the possible goal-progress/places before this are: late goal progress in place 1, late goal progress in place 3 and late goal progress in place 5; see maze structure in Fig. 1a). We used this activity to predict a binary vector that takes a value of 1 when the animal visits the anchor and 0 when the animal could have visited the anchor (that is, was one step away from it) but did not chose to visit the anchor. To remove confounds due to the autocorrelated previous behavioural choices, we added previous choices up to 10 trials in the past into the regression model. For the first regression analysis in Fig. 6b,c and Extended Data Fig. 9c, we add previous choices as individual regressors (each trial being a column in the independent variable matrix). Once we determined the regression coefficients for previous choices in Extended Data Fig. 9c, we fit an exponential decay function to these coefficients and used this kernel in all subsequent regressions in Fig. 6 and Extended Data Fig. 9 to give different weights to the previous choices depending on how many trials back they happened. This creates a single regressor that accounts for all previous choices up to 10 trials in the past. Furthermore, to assess whether any observed prediction was specific to the bump time as predicted by the SMB model, we repeated the logistic regression for other control times: random times and decision time (30° before the potential anchor visit for ABCD and 24° before potential anchor visit in ABCDE). We also do the same for times shifted by one state intervals from the bump time (90°, 180° and 270° for ABCD tasks) and (72°, 144°, 216° and 288° for the ABCDE task). This preserves the cell’s goal-progress preference but not lag from anchor, allowing us to test whether the precise lag from anchor in the entire task space is important for predictions of future choices. We further repeated this regression only taking neurons that are more distal from their anchor (that is, at least 90 degree separation either side of the anchor: Extended Data Fig. 9d) and also only for visits to non-zero goal-progress anchors (that is, non-rewarded locations: Extended Data Fig. 9e–h).

Sleep–rest analysis

To investigate the internal organization of task-related mFC activity we recorded neuronal activity in a separate enclosure containing bedding from the animal’s home cage but no reward or task-relevant cues. Animals were pre-habituated to sleep/rest in these ‘sleep boxes’ before the first task began. We measured neuronal activity across sleep/rest sessions both before any tasks on a given day and after each session. The first (pre-task) sleep/rest session was 1 h long, inter-session sleep/rest sessions were 20 min long and the sleep/rest session after the last task was 30-45 min long. All sessions except the first sleep session were designated as ‘post-task’ sleep sessions.

In the parts leading up to the sleep analysis we show that neurons are organized sequentially relative to each other (Figs. 2 and 3) and relative to anchor points (Fig. 5), firing consistently at fixed lags from these anchors. We further show task structuring of the SMBs by illustrating that neurons can be used to predict an animal’s future choices in a manner paced by the task periodicity (Fig. 6). Having established this task structured, sequential activity, what we aim to do with Fig. 7 is to test: (1) whether this sequential activity is internally organized (that is, present in the absence of any structured task input); and (2) whether internally organized sequential activity is open (creating a delay line) or closed (creating a ring).

Activity was binned in 250-ms bins and cross-correlations between each pair of neurons were calculated using this binned activity. For this analysis, we only used consistently anchored neurons, that is neurons that had the same goal-progress/location conjunction as its best anchor and same lag from this anchor in at least half of the tasks. We then regressed the awake angle difference between pairs of neurons sharing the same anchor against this sleep cross-correlation. This angle was taken from the first task on a given day for pre-task sleep, and from the task immediately before the sleep session for all post-task sleep sessions. The idea is that neurons closer to each other in a given neuronal state-space should be more likely to be coactive within a small time window compared to neurons farther apart. Thus, we assessed the degree to which the regression coefficients were negative (that is, smaller distances correlate with higher coactivity). If the distribution of lags from the anchor was uniform, forward and circular distances would be orthogonal and so adding forward distance to the regression would be redundant. However, the distribution of lags from the anchor is not uniform (Extended Data Fig. 7c) and so we add forward distance to the regression to remove any possible contribution of delay lines to the results. We measured the forward distance between pairs of co-anchored neurons in reference to their anchor. If neurons are internally organized on a line, then the larger the forward distance between a pair of neurons the further away two neurons are from each other in neuronal state space, and hence the less coactive they will be (Fig. 7a). Circular distance is correlated with forward distance for pairs of neurons with a forward distance of <180 but anti-correlated with forward distance for pairs of neurons with a forward distance of >180, as neurons circle back closer to each other if the state space is a ring. We used a linear regression to compute the regression coefficients for circular and forward distances in the same regression for all consistently anchored neuron pairs sharing the same anchor (Extended Data Fig. 10a), and when comparing those to neuron pairs across anchors (Fig. 7c). To control for place and goal-progress tuning, we added the spatial map correlation and circular goal-progress distance as co-regressors in the regression analyses.

To further analyse whether the state space is circular, we compared the sleep cross-correlation between pairs of neurons (that share the same anchor) at different forward distances. If the state space is circular, this should give a V-shaped curve, with high cross-correlations at the lowest forward distances and highest forward distances which both correspond to low circular distances. In other words, the slope of the cross-correlation versus forward distance curve should be negative for pair-to-pair forward angles <180° and positive for angles >180°. A delay line would instead give a negatively sloping curve at all pairwise angles. In line with a circular state space, we observe a V-shaped curve in Fig. 7d. Further, to investigate the effects of sleep stage or time since sleep on our results, we conducted the same analyses across pre-task and post-task sleep (Extended Data Fig. 10b) and across different times since sleep (Extended Data Fig. 10c).

We further analysed whether neurons that shared the same anchor showed stronger state-space versus sleep coactivity relationships than those that have different anchors. We conducted the regression of circular distance against sleep cross-correlation either for pairs of neurons that share the same anchor, or those that have different anchors (Fig. 7c). As before, we co-regressed spatial correlations and goal-progress distances.

Numbers

Animals: 13 animals in total were used for behavioural recordings across 4 separate cohorts conducted by 3 different experimenters (A.L.H., M.E.-G. and A.B.)—4 of these animals only completed 10 tasks as part of the first cohort and the remaining 7 completed at least 40 ABCD tasks. Three animals performed additional ABCD tasks with the tone omitted from reward a on 50% of trials. Two animals did additional ABCDE tasks.

Of the 13 animals, 7 animals in total were used for electrophysiological recordings, the remaining 6 animals are accounted for below:

• 3 animals (in cohort 1) were not implanted at any point.

• 1 animal was implanted with silicon probes but was part of the first cohort so did not get to the 3 task days (that is, only completed the first 10 tasks).

• 2 animals were implanted but their signal was lost before the 3 task days.

Exclusions: no animals were excluded from analyses: All animals (13) were included in the behavioural analyses, and all animals for which there was an electrophysiological signal by the 3 task days (7) were included in the electrophysiological analyses.

Neurons: we report ‘neuron-days’—that is, by summing up each day’s neuron yield throughout the manuscript.

Total number of neuron-days:

1. (1)

   ABCD task: 2,929 when splitting all data into single days (that is, while splitting each double day into two and summing the yield across days). (Note: this is used when the analysis pertains specifically to comparisons across 3 tasks: Figs. 2f and 3 and Extended Data Fig. 4). 1677 when considering the yield of double days only once (that is, no splitting of double days).

2. (2)

   ABCDE task: 288 neurons on concatenated double days (that is, no splitting of double days).

More detail is provided in Supplementary Table 1, which outlines the numbers of mice, recording days, tasks, sessions, neurons and neuron pairs (as appropriate) for each analysis and the criteria used for inclusion.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.