A probabilistic histological atlas of the human brain for MRI segmentation

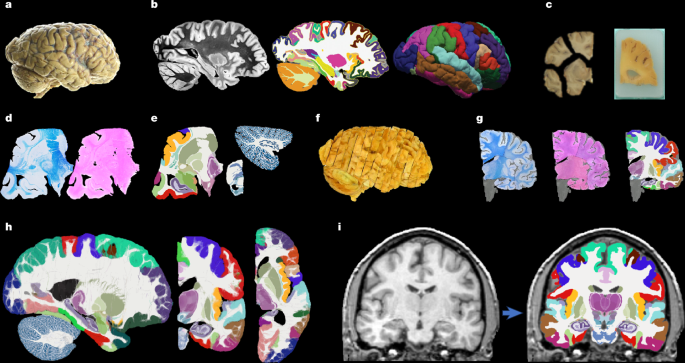
Brain specimens

Hemispheres from five individuals (including half of the cerebrum, cerebellum and brainstem), were used in this study, following informed consent to use the tissue for research and the ethical approval for research by the National Research Ethics Service Committee London – Central. All hemispheres were fixed in 10% neutral buffered formalin (Fig. 1a). The laterality and demographics are summarized in Supplementary Table 1; the donors were neurologically normal, but one case had an undiagnosed, asymptomatic tumour (diameter roughly 10 mm) in the white matter, adjacent to the pars opercularis. This tumour did not pose issues in any of the processing steps described below.

Data acquisition

Our data acquisition pipeline largely leverages our previous work²⁶. We summarize it here for completeness; the reader is referred to the corresponding publication for further details.

MRI scanning

Before dissection, the hemispheres were scanned on a 3-T Siemens MAGNETOM Prisma scanner. The specimens were placed in a container filled with Fluorinert (perfluorocarbon), a proton-free fluid with no MRI signal that yields excellent ex vivo MRI contrast and does not affect downstream histological analysis⁵⁸. The MRI scans were acquired with a T2-weighted sequence (optimized long echo train 3D fast spin echo⁵⁹) with the following parameters: TR = 500 ms, TEeff = 69 ms, BW = 558 hertz per pixel, echo spacing = 4.96 ms, echo train length = 58, 10 averages, with 400-μm isotropic resolution, acquisition time for each average = 547 s, total scanning time = 91 min. These scans were processed with a combination of SAMSEG³⁵ and the FreeSurfer 7.0 cortical stream⁵¹ to bias-field-correct the images, generate rough subcortical segmentations and obtain white matter and pial surfaces with corresponding parcellations according to the Desikan–Killiany atlas²⁹ (Fig. 1b).

Dissection

After MRI scanning, each hemisphere is dissected to fit into standard 74 mm × 52 mm cassettes. First, each hemisphere was split into cerebrum, cerebellum and brainstem. Using a metal frame as a guide, these were subsequently cut into 10-mm-thick slices in coronal, sagittal and axial orientation, respectively. These slices were photographed inside a rectangular frame of known dimensions for pixel size and perspective correction; we refer to these images as ‘whole slice photographs’. Although the brainstem and cerebellum slices all fit into the cassettes, the cerebrum slices were further cut into as many blocks as needed. ‘Blocked slice photographs’ were also taken for these blocks (Fig. 1c, left).

Tissue processing and sectioning

After standard tissue processing steps, each tissue block was embedded in paraffin wax and sectioned with a sledge microtome at 25-μm thickness. Before each cut, a photograph was taken with a 24 MPx Nikon D5100 camera (ISO = 100, aperture = f/20, shutter speed = automatic) mounted right above the microtome, pointed perpendicularly to the sectioning plane. These photographs (henceforth ‘blockface photographs’) were corrected for pixel size and perspective using fiducial markers. The blockface photographs have poor contrast between grey and white matter (Fig. 1c, right) but also negligible nonlinear geometric distortion, so they can be readily stacked into 3D volumes. A two-dimensional convolutional neural network (CNN) pretrained on the ImageNet dataset⁶⁰ and fine-tuned on 50 manually labelled examples was used to automatically produce binary tissue masks for the blockface images.

Staining and digitization

We mounted on glass slides and stained two consecutive sections every N (see below), one with H&E and one with LFB (Fig. 1d). The sampling interval was N = 10 (that is, 250 μm) for blocks that included subcortical structures in the cerebrum, medial structures of the cerebellum or brainstem structures. The interval was N = 20 (500 μm) for all other blocks. All stained sections were digitized with a flatbed scanner at 6,400 DPI resolution (pixel size 3.97 μm). Tissue masks were generated using a two-dimensional CNN similar to the one used for blockface photographs (pretrained on ImageNet and fine-tuned on 100 manually labelled examples).

In vivo ADNI data

The in vivo ADNI dataset used in the preparation of this article were obtained from the ADNI database (https://adni.loni.usc.edu/). The ADNI was launched in 2003 as a public–private partnership, led by Principal Investigator M. W. Weiner. The primary goal of ADNI has been to test whether serial MRI, positron emission tomography, other biological markers and clinical and neuropsychological assessments can be combined to measure the progression of mild cognitive impairment and early Alzheimer’s disease. For up-to-date information, see www.adni-info.org.

Dense labelling of histology

Segmentations of 333 ROIs (34 cortical, 299 subcortical) were made by authors E.R., J.A. and E.B. (with guidance from D.K., M.B., Z.J. and J.C.A.) for all the LFB sections, using a combination of manual and automated techniques (Fig. 1e). The general procedure to label each block was (1) produce an accurate segmentation for one of every four sections, (2) run SmartInterpol²⁸ to automatically segment the sections in between and (3) manually correct these automatically segmented sections when needed. SmartInterpol is a dedicated artificial intelligence technique that we have developed specifically to speed up segmentation of histological stacks in this project.

To obtain accurate segmentations on sparse sections, we used two different strategies depending on the brain region. For the blocks containing subcortical or brainstem structures, ROIs were manually traced from scratch using a combination of ITK-SNAP⁶¹ and FreeSurfer’s viewer ‘Freeview’. For cerebellum blocks, we first trained a two-dimensional CNN (a U-Net⁶²) on 20 sections on which we had manually labelled the white matter and the molecular and granular layers of the cortex. The CNN was then run on the (sparse) sections and the outputs manually corrected. This procedure saves a substantial amount of time, because manually tracing the convoluted shape of the arbor vitae is extremely time consuming. For the cortical cerebrum blocks, we used a similar strategy as for the cerebellum, labelling the tissue as either white or grey matter. The subdivision of the cortical grey matter into parcels was achieved by taking the nearest neighbouring cortical label from the aligned MRI scan (details on the alignment below).

The manual labelling followed neuroanatomical protocols based on different brain atlases, depending on the brain region. Further details on the specific delineation protocols are provided in the Supplementary Information. The general ontology of the 333 ROIs is based on the Allen reference brain³ and is provide in a spreadsheet as part of the Supplementary Information.

3D histology reconstruction

3D histology reconstruction is the inverse problem of reversing all the distortion that brain tissue undergoes during acquisition, to reassemble a 3D shape that accurately follows the original anatomy. For this purpose, we used a framework with four modules.

Initial blockface alignment

To roughly initialize the 3D reconstruction, we relied on the stacks of blockface photographs. Specifically, we used our previously presented hierarchical joint registration framework²³ that seeks to (1) align each block to the MRI with a similarity transform, by maximizing the normalized cross-correlation of their intensities while (2) discouraging overlap between blocks or gaps in between, by means of a differentiable regularizer. The similarity transforms allowed for rigid deformation (rotation, translation), as well as isotropic scaling to model the shrinking due to tissue processing. The registration algorithm was initialized with transforms derived from the whole slice, blocked slice and blockface photographs (see details in ref. ²⁶). The registration was hierarchical in the sense that groups of transforms were forced to share the same parameters in the earlier iterations of the optimization, to reflect our knowledge of the cutting procedure. In the first iterations, we clustered the blocks into three groups: cerebrum, cerebellum and brainstem. In the following iterations, we clustered the cerebral blocks that were cut from the same slice and allowed translations in all directions, in-plane rotation and global scaling. In the final iterations, each block alignment was optimized independently. The numerical optimization used the LBFGS algorithm⁶³. The approximate average error after this procedure was about 2 mm (ref. ²³). A sample 3D reconstruction is shown in Fig. 1f.

Refined alignment with preliminary nonlinear model

Once a good initial alignment is available, we can use the LFB sections to refine the registration. These LFB images have exquisite contrast (Fig. 1d) but suffer from nonlinear distortion—rendering the good initialization from the blockface images crucial. The registration procedure was nearly identical to that of the blockface, with two main differences. First, the similarity term used the local (rather than global) normalized cross-correlation function⁶⁴ to handle uneven staining across sections. Second, the deformation model and optimization hierarchy were slightly different because nonlinear registration benefits from more robust methods. Specifically, the first two levels of optimization were the same, with blocks grouped into cerebrum/cerebellum/brainstem (first level) or cerebral slices (second level) and optimization of similarity transforms. The third level (that is, each block independently) was subdivided into four stages in which we optimized transforms with increasing complexity, such that the solution of every level of complexity served as initialization to the next. In the first and simplest stage, we allowed for translations in all directions, in-plane rotation and global scaling (five parameters per block). In the second stage, we added a different scaling parameter in the normal direction of the block (six parameters per block). In the third stage, we allowed for rotation in all directions (eight parameters per block). In the fourth and final stage, we added to every section in every block a nonlinear field modelled with a grid of control points (10-mm spacing) and interpolating B-splines. This final deformation model has about 100,000 parameters per case (about 100 parameters per section, times about 1,000 LFB sections).

Nonlinear artificial intelligence registration

We seek to produce final nonlinear registrations that are accurate, consistent with each other and robust against tears and folds in the sections. We capitalize on Synth-by-Reg (SbR²⁴), an artificial intelligence tool for multimodal registration that we have recently developed, to register histological sections to MRI slices resampled to the plane of the histology (as estimated by the linear alignment). SbR exploits the facts that (1) intramodality registration is more accurate than intermodality registration with generic metrics like mutual information^65,66 and (2) there is a correspondence between histological sections and MRI slices: that is, they represent the same anatomy. In short, SbR trains a CNN to make histological sections look like MRI slices (a task known as style transfer⁶⁷), using a second CNN that has been previously trained to register MRI slices to each other. The style transfer relies on the fact that only good MRI synthesis will yield a good match when used as input to the second CNN, which enables SbR to outperform unpaired approaches²⁴ such as CycleGAN⁶⁸. SbR also includes a contrastive loss⁶⁹ that prevents blurring and content shift due to overfitting. SbR produces highly accurate deformations parameterized as stationary velocity fields (SVFs⁷⁰).

Bayesian refinement

Running SbR for each stain and section independently (that is, LFB to resampled MRI and H&E to resampled MRI) yields a reconstruction that is jagged and sensitive to folds and tears. One alternative is to register each histological section to each neighbour directly, which achieves smooth reconstructions but incurs the so-called ‘banana effect’: that is, a straightening of curved structures¹⁴. We have proposed a Bayesian method that yields smooth reconstructions without the banana effect²⁵. This method follows an overconstrained strategy by computing registrations between LFB and MRI, H&E and MRI, H&E and LFB, each LFB section and the two nearest neighbours in either direction across the stack, each H&E section and its neighbours, and each MRI slice and its neighbours. For a stack with S sections, this procedure yields 15xS-18 registrations, whereas the underlying dimensionality of the spanning tree connecting all the images is just 3xS-1. We use a probabilistic model of SVFs to infer the most likely spanning tree given the computed registrations, which are seen as noisy measurements of combinations of transforms in the spanning tree. The probabilistic model uses a Laplace distribution, which relies on L1 norms and is thus robust to outliers. Moreover, the properties of SVFs enable us to write the optimization problem as a linear program, which we solve with a standard simplex algorithm⁷¹. The result of this procedure was a 3D reconstruction that is accurate (it is informed by many registrations), robust and smooth (Figs. 1g and 2).

Atlas construction

The transforms for the LFB sections produced by the 3D reconstructions were applied to the segmentations to bring them into 3D space. Despite the regularizer from ref. ²³, minor overlaps and gaps between blocks still occur. The former were resolved by selecting the label that is furthest inside the corresponding ROI. For the latter, we used our previously developed smoothing approach⁴⁰.

Given the low number of available cases, we combined the left (2) and right (3) hemispheres into a single atlas. This was achieved by flipping the right hemispheres and computing a probabilistic atlas of the left hemisphere using an iterative technique³³. To initialize the procedure, we registered the MRI scans to the MNI atlas¹⁵ with the right hemisphere masked out and averaged the deformed segmentations to obtain an initial estimate of the probabilistic atlas. This first registration was based on intensities, using a local normalized cross-correlation loss. From that point on, the algorithm operates exclusively on the segmentations.

Every iteration of the atlas construction process comprises two steps. First, the current estimate of the atlas and the segmentations are coregistered one at a time using (1) a diffeomorphic deformation model based on SVFs parameterized by grids of control points and B-splines (as implemented in NiftyReg⁷²), which preserves the topology of the segmentations; (2) a data term, which is the log-likelihood of the label at each voxel according to the probabilities given by the deformed atlas (with a weak Dirichlet prior to prevent logs of zero); and (3) a regularizer based on the bending energy of the field, which encourages regularity in the deformations. The second step of each iteration updates the atlas by averaging the segmentations. The procedure converged (negligible change in the atlas) after five iterations. Slices of the atlas are shown in Figs. 1h and 3.

Bayesian segmentation

Our Bayesian segmentation algorithm builds on well-established methods in the neuroimaging literature^18,73,74. In short, the algorithm jointly estimates a set of parameters that best explain the observed image in light of the probabilistic atlas, according to a generative model based on a Gaussian mixture model (GMM) conditioned on the segmentation, combined with a model of bias field. The parameters include the deformation of the probabilistic atlas; a set of coefficients describing the bias field; and the means, variances and weights of the GMM. The atlas deformation is regularized in the same way as the atlas construction (bending energy, in our case) and is estimated by means of numerical optimization with LBFGS. The bias field and GMM parameters are estimated with the Expectation Maximization algorithm⁷⁵.

Compared with classical Bayesian segmentation methods operating at 1-mm resolution with just a few classes (for example, SAMSEG³⁵, SPM¹⁸), our proposed method has several distinct features:

1. (1)

   Because the atlas only describes the left hemisphere, we use a fast deep learning registration method (EasyReg⁷⁶) to register the input scan to MNI space and use the resulting deformation to split the brain into two hemispheres that are processed independently.

2. (2)

   Because the atlas only models brain tissue, we run SynthSeg⁷⁷ on the input scan to mask out the extracerebral tissue.

3. (3)

   Clustering ROIs into tissue types (rather than letting each ROI have its own Gaussian) is particularly important, given the large number of ROIs (333). The user can specify the clustering by means of a configuration file; by default, our public implementation uses a configuration with 15 tissue types, tailored to in vivo MRI segmentation.

4. (4)

   The framework is implemented using the PyTorch package, which enables it to run on graphics processing units and curbs segmentation run times to about half an hour per hemisphere.

Sample segmentations with this method can be found in Fig. 1h (in vivo) and Fig. 4 (ex vivo).

Labelling of ultra-high-resolution ex vivo brain MRI

To quantitatively assess the accuracy of our segmentation method on the ultra-high-resolution ex vivo scan, we produced a gold standard segmentation of the publicly available 100-μm scan¹² as follows. First, we downsampled the data to 200-μm resolution and discarded the left hemisphere, to alleviate the manual labelling requirements. Next, we used Freeview to manually label from scratch one coronal slice of every ten; we labelled as many regions from the histological protocol as the MRI contrast allowed—without subdividing the cortex. Then, we used SmartInterpol²⁸ to complete the segmentation of the missing slices. Next, we manually corrected the SmartInterpol output as needed, until we were satisfied with the 200-μm isotropic segmentation. The cortex was subdivided using standard FreeSurfer routines. This labelling scheme led to a ground truth segmentation with 98 ROIs, which we have made publicly available. Supplementary Videos 3 and 4 fly over the coronal and axial slices of the labelled scan, respectively.

We used a simplified version of the NextBrain atlas when segmenting the 100-μm scan, to better match the ROIs of the automated segmentation and the ground truth (especially in the brainstem). This version was created by replacing the brainstem labels in the histological 3D reconstruction (Fig. 1g, right) by new segmentations made directly in the underlying MRI scan. These segmentations were made with the same methods as for the 100-μm isotropic scan. The new combined segmentations were used to rebuild the atlas.

Automated segmentation with Allen MNI template

Automated labelling with the Allen MNI template relied on registration-based segmentation with the NiftyReg package^34,72, which yields state-of-the-art performance in brain MRI registration⁷⁸. We used the same deformation model and parameters as the NiftyReg authors used in their own registration-based segmentation work⁷⁹: (1) symmetric registration with a deformation model parameterized by a grid of control points (spacing 2.5 mm = 5 voxels) and B-spline interpolation; (2) local normalized cross-correlation as objective function (s.d. 2.5 mm); and (3) bending energy regularization (weight 0.001).

LDA for Alzheimer’s disease classification

We performed linear classification of Alzheimer’s disease versus controls based on ROI volumes as follows. Leaving out one subject at a time, we used all other subjects to (1) compute linear regression coefficients to correct for sex and age (intracranial volume was corrected by division); (2) estimate mean vectors for the two classes \(({{\mathbf{\upmu }}}_{0},{{\mathbf{\upmu }}}_{1})\), as well as a pooled covariance matrix (Σ); and (3) use the means and covariance to compute an unbiased log-likehood criterion L for the left-out subject:

where x is the vector with ICV-, sex- and age-corrected volumes for the left-out subject. Once the criterion L has been computed for all subjects, it can be globally thresholded for accuracy and ROC analysis. We note that, for NextBrain, the high number of ROIs renders the covariance matrix singular. We prevent this by using regularized LDA: we normalize all the ROIs to unit variance and then compute the covariance as \(\Sigma =S+{\rm{\lambda }}I,\) where S is the sample covariance, I is the identity matrix and \({\rm{\lambda }}=1.0\) is a constant. We note that normalizing to unit variance enables us to use a fixed, unit λ—rather than having to estimate λ for every left-out subject.

B-spline fitting of ageing trajectories

To compute the B-spline fits in Extended Data Fig. 8, we first corrected the ROI volumes by sex (using regression) and intracranial volume (by division). Next, we modelled the data with a Laplace distribution, which is robust against outliers which may be caused by potential segmentation mistakes. Specifically, we used an age-dependent Laplacian where the location μ and scale b are both B-splines with four evenly space control points at 30, 51.6, 73.3 and 95 years. The fit is optimized with gradient ascent over the log-likelihood function:

where \(p(x;\mu ,b)\) is the Laplace distribution with location μ and scale b; v_n is the volume of ROI for subject n; a_n is the age of subject n; \(\mu ({a}_{{n}};{\theta }_{{\mu }})\) is a B-spline describing the location, parameterized by θ_μ; and \(b({a}_{n};{\theta }_{b})\) is a B-spline describing the scale, parameterized by θ_b. The 95% confidence interval of the Laplace distribution is given by μ ± 3b.

Ethics statement

The brain donation programme and protocols have received ethical approval for research by the National Research Ethics Service Committee London – Central, and tissue is stored for research under a license issued by the Human Tissue Authority (no. 12198).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.