Preparation of MR yarns
We selected LDPE as the flexible matrix because of its high filler capacity enabled by highly branched chains with low molecular packing46 and good flowability indicated by a broad molecular weight distribution (Supplementary Fig. 23) and significant shear thinning (Extended Data Fig. 1a). CIP was chosen over other soft magnetic materials for its high susceptibility and low remnant magnetization, availability in micro-spherical particles, cost-effectiveness and resistance to oxidation with SiO2 coating (Supplementary Table 2). CIPs coated with SiO2 (SQ, BASF SE; Supplementary Fig. 24) were dispersed within LDPE (1700 MN 18C, total energies SE; melt flow rate of 70 g/10 min at 190 °C/2.16 kg) by melt compounding by a twin-screw extruder (Thermo Fisher Hot Melt Extruder Pharma 11). The temperature profile, ranging from the hopper to the die, was set at 10, 80, 130, 150, 150, 150, 150, 150, and 150 °C, respectively, while the screw speed was kept at 50 rpm. Four LDPE/CIP composites were prepared, varying in CIP content at 30, 50, 70, and 80 wt%. Interfacial interactions between LDPE molecules and CIPs (Supplementary Note 8 and Supplementary Fig. 25) promote the wetting of polymer on CIP surfaces, ensuring the uniform CIP dispersion of composites with filler content up to 80 wt% (Extended Data Fig. 7). Among these, the composite containing 70 wt% CIPs was chosen for fibre spinning.
This selected composite was introduced into the barrel of a laboratory melt spinning machine (AT225, Anytester Hefei) to produce MR fibres. The three heating zones of the barrel were set at 140 °C, 150 °C and 160 °C, respectively, allowing the composites to melt for 10 min until reaching a stable temperature of 160 °C. Nitrogen was then filled into the barrel to provide a pressure of 1.2 MPa. The molten polymer strands were extruded through a spinneret and guided by a ceramic wheel onto a collection roller with a diameter of 8.2 cm. A cooling fan positioned between the spinneret and the guide wheel facilitated solidification of the molten composite fibres. The diameter of the resulting MR fibre could be controlled by adjusting the winding speed, and in this case, the extruded molten filaments with a diameter of 750 μm underwent rapid thinning over a short range of about 20 cm (Extended Data Fig. 3). MR fibres with a diameter of 57 μm were consistently produced at a winding speed of 130 rpm. Then, seven of these fully drawn fibres were twisted clockwise to form a yarn, which was subsequently heat-set in an oven at 60 °C for 1 h to alleviate residual stress and stabilize the twist configuration. The primary goal in optimizing the structure of MR yarn was to maximize Ay/Iy, which is inversely related to the diameter of the fibres and directly related to the helical angle of the yarn (Supplementary Note 1). Given that the fibre diameter directly correlates with its modulus, our evaluation focused on optimizing Ay/EIy to refine the MR yarn design.
Fabrication of MR fabrics
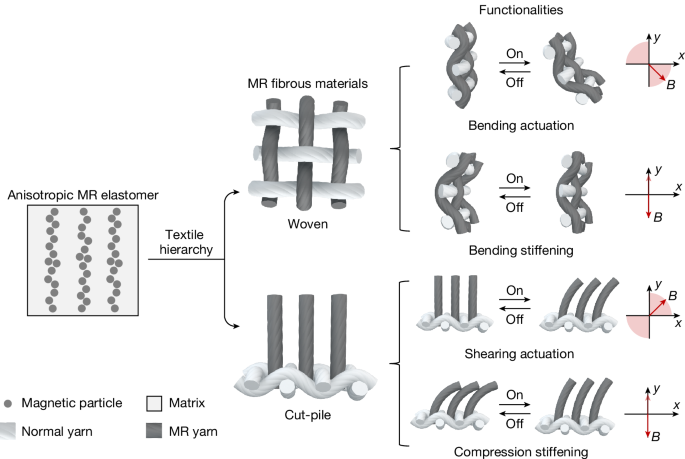
Woven MR fabrics were fabricated by interlacing MR yarns as weft and sewing thread as warp at right angles, using a hand weaving machine. Float lengths of 1, 2 and 4 were specifically chosen to fabricate plain-, twill-, and satin-weave MR fabrics that exhibit packing densities of 65 yarns cm−1, 83 yarns cm−1, and 111 yarns cm−1, respectively (Extended Data Fig. 8). These selections enable the examination of the spatial freedom of interlacing MR yarns concerning their float length and packing density. The plain weave has the highest number of interlacing points, followed by the twill weave, and the satin weave.
Cut-pile MR fabrics were fabricated by inserting MR yarns into holes of a base plain-weave fabric using a punch needle kit. On pulling the needle out, a loop of MR yarn formed on the opposite side, its length controlled by the depth of needle insertion. This process repeated until the predefined area was uniformly filled at yarn densities of 250 yarns cm−2 or 500 yarns cm−2. Subsequently, a thin layer of silicone glue was applied to secure the inserted yarns. The loops were then cut at their centre points, followed by the application of silicone precursor at the cut tips. After curing overnight at room temperature, the silicone effectively prevented the free ends from untwisting.
Coefficient of friction
The as-spun filaments, each with a length of 3 cm, were arranged in parallel without any gaps to form a 1-cm wide region and adhered onto a square glass measuring 3 cm × 3 cm and weighing 1.8 g using a double-sided tape. Two identical samples were prepared for the measurement: one with the filaments facing upwards, and the glass side fixed onto a horizontal linear platform, and the other sample with the filaments facing downwards, aligned face-to-face and parallel to the filament region of the first sample. At the left edge of the top glass packed with filament tips, the centre point of the glass edge was horizontally connected to a force gauge using a nylon filament. A series of weights (1 g, 2 g, 5 g, 10 g, 20 g, 50 g and 100 g) were separately placed on top of the sample to provide normal force Fnf = mtmg, where mtm is the total mass of the weight and top glass substrate, and g is the acceleration due to gravity. The linear platform moved away from the force gauge at a velocity of 5 µm s−1. The maximum reading of the force gauge was recorded as the maximum static friction Ffriction, and the static friction coefficient a was calculated using the formula: Ffriction = aFnf. The static coefficient of friction between MR fibres was measured in the same way, by replacing the filaments with fibres.
Differential scanning calorimetry
Differential scanning calorimetry experiments were conducted using a Mettler Toledo DSC3 in a nitrogen atmosphere. Each sample, weighing approximately 1.5 mg, was analysed within a temperature range of 55–135 °C at a heating rate of 10 °C min−1 to record the endothermic curves. The heat of fusion (ΔHf) was determined by integrating the heat flow between 60 °C and 115 °C. This parameter was then used to calculate the crystallinity degree (χ) of both pure LDPE and the composite matrix. The crystallinity degree χ was defined as the ratio of ΔHf/(1 − x), where x represents the content of CIPs in the composite, to the heat of fusion (289.9 J g−1) of the purely crystalline form of polyethylene47.
MR fibre thermal shrinkage
MR fibre shrinkage was assessed by subjecting the MR fibres with a length of 30–50 mm to a temperature of 100 °C for 10 min without external constraints. Shrinkage was quantified as the percentage change in the original MR fibre length using the formula, Shrinkage (%) = 100 × (Lif − Lsf)/Lif, where Lif represents the initial fibre length and Lsf represents the fibre length after complete shrinkage. The thermal shrinkage results provide insights into both the elongation and arrangement of polymer chains within the MR fibres. This is attributed to the relaxation of polymer chains during the thermal shrinkage process.
Tensile measurement
LDPE and composites containing 30 wt%, 50 wt% and 70 wt% CIPs samples with a dimension of 30 × 10 × 0.105 mm3 were stretched to break at a velocity of 0.3 mm s−1 by a universal testing machine (Model 5566, Instron).
Structure characterization
Scanning electron microscopy images were obtained using a Tescan VEGA3 microscope equipped with an energy dispersive X-ray spectroscopy detector. Polymer composite samples were subjected to freeze fracture in liquid nitrogen to expose the cross-sectional surfaces, and then sputter coating was done with Au. The imaging was conducted at an accelerating voltage of 20 kV. The energy dispersive X-ray spectroscopy mapping was performed to analyse the distribution of Si, O and Fe on the surface of CIP. Optical photographs were captured using a Leica M165 C High-Performance Stereo Microscope to visualize the structure and extract the geometrical parameters of yarns and fabrics. Nano-computed tomography analysis was conducted using a Zeiss Xradia 520 Versa 3D X-ray microscope to examine the distribution of CIPs within the MR fibre. An MR fibre, approximately 1 mm in length, was mounted on the sample stage. Cross-sectional images, each with a resolution of 480 nm, were sequentially captured along the length at specified intervals. These images were then processed to generate a 3D reconstruction of the MR fibre. The polymer matrix was then extracted, in which the white zones represent CIPs. The directional distribution of CIPs within the MR fibre was assessed using ImageJ software with the following processing steps48. Initially, the raw nano-computed tomography images of both transverse and longitudinal sections were converted into binary images using an appropriate threshold to delineate the CIP distribution. Subsequently, the adjustable watershed algorithm was applied to segment the binary image effectively. The areas reflecting concentrated CIPs appeared as white zones within the images and were then fitted with ellipses to account for any orientation in the CIP distribution. Finally, the orientation of each CIP-concentrated area was determined by measuring the tilt angles of the ellipses relative to the horizontal plane. The degree of orientation was analysed based on the percentage distribution of different angles.
Magnetization characterization
Magnetic measurements were conducted at room temperature using the Physical Properties Measurement System (Quantum Design) with a sweep of external magnetic field ranging from −13 kOe to 13 kOe. Samples, including CIPs, LDPE, and composites with CIP contents of 30 wt%, 50 wt%, and 70 wt%, were tested without any preferred direction. The MR yarn was tested twice with the axis oriented parallel and perpendicular to the direction of the applied magnetic field.
Oscillatory shear rheology
Dynamic rheological characterization of both neat LDPE and composites was conducted using a rheometer (AR 2000EX, TA Instruments) equipped with parallel plate geometry. The samples were compressed into disc-shaped specimens with a thickness of 2 mm and a diameter of 25 mm for testing purposes. Frequency sweeps were performed at 160 °C, with the frequency ranging from 100 Hz to 0.01 Hz, while maintaining a strain of 0.5% within the linear viscoelastic region.
Dynamic mechanical analysis
Dynamic mechanical analysis experiments were carried out using a Mettler Toledo DMA1. Samples of LDPE and composites containing 70 wt% CIPs were analysed from −150 °C to −50 °C at a heating rate of 5 °C min−1 to record tan δ curves.
Bending actuation characterization
The bending property of MR yarns was characterized by subjecting vertically cantilevered MR yarns, anchored at their top end, to uniform magnetic fields. MR yarns were cantilevered at the top and positioned vertically within the central space between the two poles of an electromagnet (PEM-20, Litian Magnetoelectrican Science & Technology). The desktop electromagnet measures 260 mm (length) × 180 mm (width) × 200 mm (height) with two 40 × 40 mm poles spaced at an adjustable distance of 0–60 mm (Supplementary Fig. 26a). Within the space between poles, highly uniform magnetic fields can be generated with controllable strength by varying the current and the pole distance (Supplementary Fig. 26b–e). This stationary device allows for precise and uniform magnetic field adjustments across a wide range, providing a versatile workspace for material property characterization and testing in various applications. Static magnetic fields were oriented at 87° to the yarn axis to control the direction of bending; as the magnetic field strength increased, the cantilevered MR yarns gradually bent upwards (Supplementary Fig. 27a). The bending deformation was captured using a camera, and the images were processed using ImageJ to quantify the bending degree. MR yarns with lengths of 10 mm, 15 mm and 20 mm were tested.
To measure the moment output of a MR yarn with length Lyarn and weight myarn, a thin paperboard strip, of weight mps, was attached along the entire free portion of the cantilevered MR yarn (Supplementary Fig. 27b). The magnetic field strength was set to specific values (70 mT, 140 mT, 210 mT, 280 mT and 300 mT), and the cantilevered MR yarn lifted until the midpoint was blocked perpendicular by the PMMA rod connected to the force gauge. At this point, the yarn formed a 45° angle with the vertical direction. The force Fblock required to block the midpoint was recorded. The moment density of the MR yarn was calculated as Mpm = Mbending/myarn = [(mps/myarn + 1)g sin 45° + Fblock]Lyarn/2. The output moment per unit mass of fabrics was measured in a similar way by using woven MR fabrics with float lengths of 1, 2 and 4 measuring 20 × 5 mm with MR yarns aligned along the length direction. For each float length, three independently fabricated samples were evaluated separately.
Stiffening characterization
The MR yarns with a length of 25 mm were measured by a three-point bending test (Supplementary Fig. 28). The lower anvil with a gap of 15 mm was fixed onto an acrylic tube, which was placed on the pan of an analytical balance (ME204, Mettler Toledo) to record the force. To prevent magnetic interference with the balance, a PMMA support with a height of 25 cm was placed beneath the three-point bending support anvil. The upper anvil was connected to an Instron, which provided a downward displacement of 3 mm and returned to the starting position at the rate of 0.1 mm s−1. Three samples of each type of yarns were tested separately. Magnetic fields were generated by a pair of N52 cylindrical magnets (diameter 70 mm and thickness 30 mm) placed parallel to the opposite poles face to face. The magnetic field strength was controlled by the distance between the two magnets. The woven MR fabrics were tested in a similar way by using a load cell (2530-10N) for recording the force.
Bending durability test
The bending durability of the MR yarn was evaluated using a continuous bending setup (Supplementary Fig. 29). A 30-cm sample was fixed at one end to a vertical glass surface. The yarn was threaded horizontally through two pairs of guide pulleys (diameter 13.76 mm) spaced 8 cm apart, followed by a single pulley (diameter 17.2 mm) mounted on a PMMA plate. A pre-tension of 32.7% of the breaking strength of the yarn was applied to the free end using a hook-weight assembly. A pair of guide pulleys (diameter 13.76 mm) was attached to a moving PMMA fixture on an Instron testing machine, programmed to cyclically bend the yarn 90° upwards and 90° downwards for around 5,000 cycles at 0.25 Hz.
Creep test
A plain-weave MR fabric (35 mm × 40 mm) with MR yarns aligned lengthwise was fixed at both ends with a 30-mm gap. A 100-g load on a PMMA block (3.25 g) applied a uniform pressure of 2.95 MPa over an area of 35 mm × 10 mm across the fabric centre. Initial deflection on loading was 0.84 mm, with no observable creep within 1,000 s. Under a magnetic field of 178 mT along the MR yarn axis, the initial deflection of the fabric decreased because of magnetic stiffening, with minimal creep observed over the same period.
A cut-pile MR fabric (40 mm × 40 mm) with a 4-mm-thick MR yarn layer was uniformly pressed with a pressure of 0.71 MPa by a loading of 113.6 g on the MR yarn layer, its thickness decreased to 3.65 mm. No additional thickness reduction occurred across 1,000 s, and under a vertical magnetic field of 187 mT, the initial compression decreased with no detectable creep on this timescale.
Finite-element analysis
A 3D model was constructed using the Magnetomechanical node of COMSOL Multiphysics. Two rectangular magnets measuring 300 μm × 300 μm × 50 μm were built face to face to provide uniform magnetic fields. The surrounding air domain is modelled as a sphere with a radius of 2,300 μm. The two permanent magnets and air domain were from the COMSOL material library, and the mechanical and magnetic properties of the MR yarn were entered based on the experimental results.
Linear actuator fabrication and test
The basic concept uses radially symmetric woven MR fabrics, each resembling a hinge, with a shared wrap yarn acting as a pivot to couple axial force to the bending moments of the woven MR fabrics. The linear fabric actuator was fabricated by integrating four plain-weave MR fabric hinges in the form of a four-sided Sarrus linkage. Each plain-weave MR fabric hinge was assembled by two plain-weave MR fabrics, measuring 5 mm × 5 mm, which shared the same wrap yarn as a pivot. To measure its stroke and force output, the linear actuator was placed on a PMMA plate within a vertical magnetic field (Supplementary Fig. 30). Initially, the actuator was fully extended, with the horizontal part of the PMMA fixture touching its top surface without force. An Instron machine then applied a downward displacement of 5 mm at 0.25 mm s−1, pressing the actuator down and recording its upward force on the PMMA fixture. After each test, the PMMA fixture returned to the starting position by the Instron machine. At the same time, the linear actuator also returned to the starting configuration due to the magnetic actuation.
Ventilation fabric demonstration
The linear actuator was sandwiched in the centre between an elastic fabric with slits and a breathable woven fabric, with an annulus of spacer fabric stitched at the edge to form a dis-shaped active ventilation fabric with a diameter of 90 mm and a thickness of 5 mm.
The water vapour permeability (WVP) of active ventilation fabric was measured according to BS 7209. The active ventilation fabric with elastic fabric facing upwards was firmly fixed on top of a glass vessel (diameter 70 mm) filled with about 30 g distilled water and operated under square-wave actuation at frequencies of 0 Hz, 0.2 Hz, 0.5 Hz, 1 Hz and 2 Hz with a peak magnetic field strength of 250 mT for 30 min. The WVP is calculated as WVP = M/(At), where M is the water loss in mass, t is the time duration and A is the area of the exposed fabric.