Sample collection
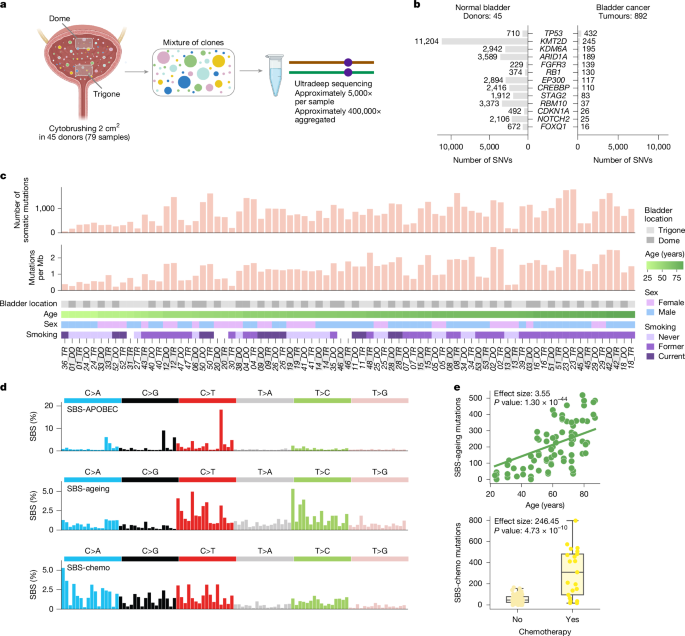
Two epithelial brushes (2–3 cm2) from the bladder top (dome) and the bladder floor (trigone) were obtained from 53 people without known bladder pathology and no history of bladder cancer upon autopsy (average 4 days post-mortem) at the University of Washington. Next of kin consented to autopsies and research on leftover specimens. The study of de-identified collected specimens and linked clinical history from the deceased donors was reviewed and deemed not human subjects research by the University of Washington Institutional Review Board (STUDY00016707; IRB Federal Wide Assurance number, FWA 00006878). We obtained the following relevant clinical information for all donors: age, sex, BMI, tobacco smoking history, alcohol use, previous cancer and chemotherapy exposure (Supplementary Table 1). Three donors with active or chronic inflammation and four donors with insufficient DNA were discarded. The two samples from another donor were also discarded from the study upon visual inspection of their mutational profile, resulting in a total of 45 deceased donors in this study (Supplementary Notes 2 and 3).
Duplex DNA sequencing
Capture panel design
We designed a panel including ten genes identified in a previous study as being under positive selection in the normal urothelium and with more than ten mutations across the 1,647 microbiopsies analysed10. We added five genes that are mutated frequently in bladder tumours30 and the TERT promoter—also known to be under positive selection in bladder carcinomas22,23. This resulted in a panel containing the entire (or almost entire) coding region of 12 genes (ARID1A, NOTCH2, FOXQ1, CDKN1A, KMT2D, RB1, CREBBP, TP53, EP300, KDM6A, RBM10 and STAG2), three genes for which only selected regions were targeted because of clustering of cancer mutations in those regions and/or difficulties for capturing the full gene (PIK3CA, FGFR3 and KMT2C) and the TERT promoter10,61. The panel was constructed by TwinStrand Biosciences and covered 111,876 base pairs, including 65,086 base pairs in coding regions and 46,790 base pairs in non-coding regions (Supplementary Tables 2 and 3 and Supplementary Note 2).
DNA extraction, duplex library preparation and sequencing
After centrifugation of epithelial brushes, DNA was extracted using the DNeasy Blood and Tissue (Qiagen) kit, following manufacturer’s instructions with some variations (Supplementary Note 2). The DNA integrity number (DIN) was measured using Agilent 4200 TapeStation Genomic tapes. Duplex sequencing libraries were prepared using commercially available kits (TwinStrand Biosciences)13,14,62,63,64 and 250 ng of genomic DNA. The DNA fragmentation step was carried out taking into account the starting DIN of samples and monitored using TapeStation. Fragmented DNA was subject to end-repair, A-tailing, ligation to duplex sequencing adaptors, library conditioning and PCR amplification, according to protocol. The PCR product was captured at 65 °C for 16–20 h. Upon PCR amplification, libraries were pooled for sequencing. Sequencing was performed with a NovaSeq 6000 at the Department of Laboratory Medicine and Pathology at University of Washington or a NovaSeq X Plus at Novogene or the Fred Hutchinson Cancer Center using 2 × 150 base-pair paired-end reads (around 115 million reads per sample; Supplementary Note 2).
Duplex DNA sequencing was successful for 34 donors on both samples. For 11 other donors, we produced duplex DNA sequencing data only for dome or trigone because of insufficient DNA or too fragmented DNA (DIN < 1.4) in the paired sample. Thus, the final number of donors with available data for at least one sample was 45 (Supplementary Table 1) and the final number of samples processed was 79 (Supplementary Table 4).
Somatic mutation calling
We constructed a computational pipeline (deepUMIcaller) in Nextflow65 to call mutations from duplex sequencing data on the basis of an early version of nf-core/fastquorum pipeline66, which implements the fgbio Best Practices FASTQ to Consensus Pipeline (https://github.com/fulcrumgenomics/fgbio/blob/main/docs/best-practice-consensus-pipeline.md) and downstream variant calling by VarDictJava (https://github.com/AstraZeneca-NGS/VarDictJava). A series of filters to discard potential artefacts are included in the pipeline. Code implementing deepUMIcaller is available at (github.com/bbglab/deepumicaller). For a detailed description of the pipeline, see Supplementary Note 3.
To estimate the error rate of TwinStrand DNA duplex sequencing, we compared the density of mutations and mutational profile identified across three cord blood samples (purchased from StemCell) with that expected on the basis of colonies obtained from human haematopoietic stem cells67,68. The estimated error rate resulting from this analysis was around 4 × 10−8, which is two orders of magnitude lower than the mutation density across samples in this study (Extended Data Fig. 2a and Supplementary Notes 4 and 8).
Mutational signatures
De novo signature extraction
We extracted mutational signatures de novo with a Bayesian hierarchical Dirichlet process using HDP_sigExtraction pipeline (https://github.com/McGranahanLab/HDP_sigExtraction) and the R-package hdp developed by N. Roberts (https://github.com/nicolaroberts/hdp)9 and SigProfilerExtractor (https://github.com/AlexandrovLab/SigProfilerExtractor)26. The HDP_sigExtraction pipeline was run with the default parameters with no previous signatures assigned. Five signatures in addition to the null signature were extracted. De novo signatures were extracted using SigProfiler using the nonnegative matrix factorization approach. The same input data were used. The upper bound for the number of signatures was set to ten; however, the most robust solution was three signatures that were similar to the three most active signatures extracted by HDP. These two sets of mutational signatures were decomposed into known COSMIC signatures when possible (Supplementary Note 5).
Assessing biases in trinucleotide composition of the panel
To account for biases due to the trinucleotide composition of the panel, the number of substitutions of each class was re-calculated. The rate of each substitution was calculated as the number of observed substitutions with the consequence in question divided by the number of corresponding sequenced trinucleotide sites (number of trinucleotides with this consequence in the panel weighted by sequencing depth). This mutational probability was multiplied by the number of the corresponding trinucleotide in the genome to get the expected number of substitutions of this type in the whole genome. The mutational probability of each substitution for the whole genome was calculated by dividing the expected number of substitutions with this consequence per genome by the sum of all expected substitutions per genome. Finally, the expected number of substitutions with each consequence was obtained by multiplying the probability by the total number of substitutions observed in the sample to keep the absolute number of observed mutations.
Statistical association between mutational signatures and clinical variables
We tested for possible associations of de novo extracted signatures with age, sex and bladder location. To do this we used linear mixed-effect regression models (Supplementary Note 5). We tested both the number of mutations attributed to the signature (counts) and the relative contribution (proportion) of each signature as a response variable. Age, sex and bladder location were used as fixed effects (separated regression was prepared for each fixed effect variable) and donors were used as random effects to control for non-independence between dome and trigone samples from the same person. P values for the association were obtained using likelihood-ratio tests (ANOVA function) comparing models including and excluding the variable of interest. Associations with all other clinical variables (smoking history, drinking history, chemotherapy history, and so on) were tested in the same way but always including age, sex and bladder location in the regression together with the variable of interest.
Positive selection
We used four methods to compute positive selection on the mutations observed across genes. One method (Omega)—a dN/dS approach to assess the strength of selection on the mutational pattern of genes—was developed de novo for this study and is described at length in Supplementary Note 6 (https://github.com/bbglab/omega). Two others, OncodriveFML and Oncodrive3D, which compute the deviation in the average functional impact and clustering in the three-dimensional structure of proteins, respectively, from those expected under neutrality, had been developed previously, and were adapted here to work on duplex sequencing data. These are also described in Supplementary Note 6. A fourth method, assessing the relative enrichment for frameshift indels observed across genes was also developed de novo for this study and is described thoroughly in Supplementary Note 6. For the TERT promoter, all mutations that were observed at least twice across 8,136 whole-genome sequencing tumour samples sequenced by the Hartwig Medical Foundation and the Pan-Cancer Analysis of Whole Genomes consortium (Supplementary Note 6) were considered activating. The remaining mutations were used to calculate the expected number of activating mutations under neutrality.
Fraction of the urothelium covered by clones with driver mutations
The number of missense and truncating driver mutations of each gene in a sample was obtained from the dN/dS missense and dN/dS truncating values. From these values the number of missense and truncating mutations in excess in each sample were calculated. Specifically, the 95% confidence intervals of both dN/dS values were used to compute two extreme values of driver mutations in each sample, whereas the mean dN/dS value was used to compute an expected number of driver mutations.
This mean number was thus used to select the most likely driver mutations in the sample. To this end, mutations were ranked in descending order according to their VAF, and the top number of mutations corresponding to the expected number of driver mutations were selected. Then, for a gene G, we computed the fraction of genomes bearing driver mutations out of those sequenced at each genomic position covered by the DNA duplex sequencing as:
$$P(G)=\mathop\sum \limits_i=1^n(-1)^i-1\sum _\prod _x\in Sp_x=\sum _xp_x-\sum _x\ne yp_xp_y+\cdots +(-1)^n-1p_x_1p_x_2\cdots p_x_n$$
where px is the all-molecules VAF of a driver mutation x (considering both duplex and non-duplex reads; Supplementary Note 3) and n is the number of driver mutations from the previously selected set in the gene. The formula is the realization of the probabilistic principle of inclusion-exclusion assuming independence across mutations69.
The fraction of genomes with driver mutations is equal to the fraction of cells with driver mutations under the assumption that two mutations, one in each homologous copy of the gene, are required to drive the clonal expansion. This extreme would be true in the case that all studied genes behave as classical tumour suppressors and bear deleterious mutations in both alleles. An exception to this rule are the mutations in genes in the X chromosome in men, whereby one mutation would suffice to drive the clonal expansion. In general, it is possible for some genes to be capable of driving the clonal expansion (or mutations at specific positions in a gene) with only one mutated allele. It is also possible that the other allele is affected by a large deletion or methylation event not seen by DNA duplex sequencing. In the extreme that only one mutation per cell per gene is required, the fraction of cells with driver mutations will be double the fraction of genomes. In the plot in Extended Data Fig. 5b, we use the two-hit assumption.
Association of the urothelium clonal structure with bladder cancer risk factors
We designed a two-step strategy to assess the influence of known bladder cancer risk factors on features of the urothelium clonal structure across samples from donors in the cohort. As dependent variables representing the urothelium clonal structure, we selected the (protein-affecting and non-protein-affecting) mutation density, and the magnitude of positive selection on genic mutations (dN/dS missense and dN/dS truncating). As the dependent variables are continuous, we chose linear regressions, specifically mixed-effects linear models, to account for two samples from the same donor and use all available samples. As independent variables, we included a list of available clinical features: age (in decades), sex, smoking history (binarized as ever or never smoker), alcohol consumption history (also binarized), BMI (re-scaled within the 0–1 interval), and exposure to chemo/radiotherapy (binarized). For the case of TERT promoter mutation density association, we used the interaction of age and smoking history instead of age and smoking history separately. In the first step, we applied univariate mixed-effects linear models to identify any clinical feature with a significant association with any of the dependent variables for any gene or for all genes. In the second step, we applied multivariate mixed-effects linear models to rule out confounding effects for the associations that seemed significant in the first step. Associations with FDR below 0.2 were deemed significant. We also carried out a binomial test to rule out a spurious dependence of the mutation density on group differences in terms of sequencing depth. For details, see Supplementary Notes 9 and 10.
Tumour data
Mutations identified across 622 muscle-invasive and 105 non-muscle-invasive bladder cancer (MIBC and NMBIC, respectively) cohorts were downloaded from cBioPortal49,70,71,72,73 together with the clinical data of the combined study. From the MIBC Beijing Genomics Institute cohort74 only samples labelled as invasive were considered MIBC and added to the MIBC dataset. Mutations identified in a further cohort of 79 NMIBCs were obtained from the literature40 and included as part of the NMIBC dataset. Only non-silent protein-affecting mutations in 14 of the genes included in the panel were analysed. In case of duplicated samples across MIBC and NMBIC cohorts, the mutations from the most recent published study were kept. In total, mutations across 806 bladder tumours were obtained (622 MIBC and 184 NMIBC). The mutation density per gene across the two datasets was calculated by dividing the number of observed mutations per gene by the length of its coding region. To compute a mutation density metric comparable with that used in the normal urothelium that accounts for the number of megabases sequenced, we multiplied the coding length by two times the number of samples in which that gene was sequenced, to take into account the two copies in a diploid genome. Under the assumption that, in tumours each mutation belongs to a single clonal expansion and in normal tissues we have a mixture of clones, we reasoned that the number of different tumour genomes sequenced would be equivalent to the number of genomes sequenced in normal urothelium. The mutation density per megabase was calculated multiplying the mutation density by 106.
Mutations identified across 33,218 tumours (892 bladder tumours, mostly MIBC) in intOGen24 were downloaded from intogen.org. These mutations were used to obtain the total number of mutations observed in each gene, their distribution along the sequence of the genes in the study and the percentage of sites affected by different numbers of mutations. The same data of 109,017 tumours (3,909 bladder tumours) were obtained from the GENIE project50 to calculate the frequency of mutations in each of the genes and the TERT promoter. Mutations in the TERT promoter were also obtained from two cohorts of tumours (included in intOGen) sequenced at the whole-genome level (Hartwig Medical Foundation21: N = 5,582 and Pan-Cancer Analysis of Whole Genomes19: N = 2,554). The classification (and score) of all possible mutations in TP53 into drivers and passengers through in silico saturation mutagenesis was obtained from boostDM (intogen.org/boostDM). Details of analyses involving tumour mutations appear in Supplementary Note 11.
Natural saturation mutagenesis
To compare the distribution of somatic mutations along the sequence of each of the genes in normal urothelium and bladder tumours, we first downloaded somatic mutations identified across 892 bladder tumours from the intOGen (intogen.org) platform. Although this cohort is larger than the 806 muscle-invasive and non-muscle-invasive tumours used to explore differences in mutation density, it is composed mostly of muscle-invasive carcinomas.
For each gene, we started the analysis with all genomic sites in the coding sequences and splicing sites that passed the pipeline’s filtering criteria of sufficient duplex coverage across samples (Supplementary Note 3). We then mapped these DNA sites to protein positions using the Ensembl REST API75, allowing us to determine the total number of protein positions (including amino acid residues and stop codon) covered by the panel. Then, we computed the number of mutations affecting each protein residue of every gene studied here across the 79 normal urothelium samples and the 892 bladder tumours. Next, we obtained the consequence type (missense, synonymous, nonsense or splice-affecting) of these mutations on the MANE transcript76 of each gene from the output of the Variant Effect Predictor v.111 (ref. 77), run within the intOGen pipeline24 (https://github.com/bbglab/intogen-plus). The method to compute the natural saturation mutagenesis kinetics in Fig. 5b is described in Supplementary Note 12. The residue-level sequencing depth shown in Fig. 5c, Extended Data Fig. 9d and Supplementary Figs. 2 and 3 was calculated as the average depth across all sites corresponding to each codon.
Calculation of site selection
We developed a metric to measure selection per site by comparing the observed with the expected number of mutations at each site or residue. The expected number of mutations per site was obtained by distributing the expected number of mutations in a given gene under neutrality along all the possible changes in that same genomic region, with the assumption that only the mutation probability of each trinucleotide and the sequencing depth are responsible for the within-gene differences of mutation probability. We computed this value for each possible mutation in the positively selected genes including the TERT promoter, and for the protein-coding genes we also obtained a value per residue. A more complete explanation on this metric (and the detection of positive selection in sub-genic structures such as exons and domains) can be found in Supplementary Note 6.
Structural representation and features
Structural models for all proteins used to run Oncodrive3D were obtained from the AlphaFold database (AlphaFold 2 v.4)78,79. Three-dimensional protein structures and protein structural features represented across figures were also obtained from the AlphaFold database. Solvent accessibility and secondary structure information were extracted from the AlphaFold-predicted PDB structures using PDB_Tool (https://github.com/realbigws/PDB_Tool). Structural visualizations of proteins were produced using UCSF ChimeraX80.
Comparison with experimental saturation mutagenesis
The results of two saturation mutagenesis experiments estimating the functional impact of mutations in the TP53 DNA-binding domain51 and along the sequence of the TERT promoter55 were obtained directly from supplementary tables from both papers. In the case of TP53, we used the transformed score. In the case of the TERT promoter, values calculated for the glioblastoma SF7996 cells system were used. In these comparisons, the site selection of individual mutations was used.
Comparison of orthogonal studies of normal bladder
We obtained the mutations identified through whole-genome sequencing in clonal or quasi-clonal samples obtained from the normal bladder of donors by laser capture microdissection in a previous study10. We used these samples to construct the mutational profile of normal urothelium, which we compared with that reconstructed in the present study through ultradeep sequencing (Extended Data Fig. 2b). From the same previous study, we obtained the mutations identified through whole-exome sequencing. Mutations obtained from samples sequenced at depth lower than 80× were discarded. From these data, we calculated the number of mutations per megabase observed in each sample, and averaged this value across donors. A linear regression was then constructed between these values and the age of donors, and a trend line calculated. The number of mutations per megabase calculated across the samples in our cohort was overlaid upon the obtained regression. The results of this comparison are presented in Extended Data Fig. 2c.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.