Marcus kinetics control singlet and triplet oxygen evolving from superoxide

Materials

All chemicals were from Sigma Aldrich unless indicated differently. Potassium superoxide (KO₂), potassium perchlorate (KClO₄, ≥99.99%), lithium bis(trifluoromethanesulfonyl)imide (LiTFSI, 99.99%) and tetrabutylammonium bis(trifluoromethanesulfonyl)imide (TBATFSI, ≥99.0%) were dried under reduced pressure for 24 h at 100 °C. Decamethylferrocene (DMFc), tris[4-(diethylamino)phenyl]amine (TDPA), N,N,N′,N′-tetramethyl-p-phenylenediamine (TMPD), ferrocene (Fc), ferrocenium tetrafluoroborate (FcBF₄), 9,10-diphenylanthracene (DPA), 1,4-bis(diphenylamino)benzene (DPAB), thianthrene (ThA), 1,4-dimethoxyanthracene (DMeOA, Acros Organics), 1,4-di-tert-butyl-2,5-dimethoxybenzene (tMeOB, BLDpharm) and 5,10-dihydro-5,10-dimethylphenazine (DMPZ, TCI chemicals) were used as received. N-methyl phenothiazine (MPT), 1,4-diazabicyclo[2.2.2]octane (DABCO) were sublimated. 18-Crown-6 and tetrafluorobenzoquinone (F₄BQ) were recrystallized from ethanol. Tetraethylene glycol dimethyl ether (TEGDME, ≥99%) was dried over lithium, distilled under vacuum and further stored over activated 3 Å molecular sieves. Acetonitrile (MeCN, 99.8% anhydrous) was stored over activated molecular sieves. Both solvents had a water content below 5 ppm as determined by Karl–Fischer titration (Mettler Toledo). All non-aqueous experiments were performed in an Ar-filled glovebox (Vigor) or hermetically sealed setups without air exposure. The structures of the mediators and their redox potentials are shown in Extended Data Fig. 2.

Electrochemistry and mediator oxidation

Electrochemistry experiments were performed using a BioLogic potentiostat (SP-300 and MPG-2). Cyclic voltammetry was performed with a glassy carbon disk as the working electrode and a glassy carbon rod as the counter electrode in a one-compartment glass cell. Partially delithiated Li_(1–x)FePO₄ (LFP, MTI), separated by a Vycor glass frit, was used as the reference electrode. DMFc/DMFc⁺ was used as the internal standard and converted using \({E}_{{\rm{DMFc}}/{{\rm{DMFc}}}^{+}}^{\circ }={E}_{{\rm{Li}}/{{\rm{Li}}}^{+}}^{\circ }+3.16\,{\rm{V}}={E}_{{\rm{K}}/{{\rm{K}}}^{+}}^{\circ }\)\(+3.02\,{\rm{V}}.\) DMeOA, tMeOB, DPA and ThA were electrochemically oxidized in an H-cell. The oxidation compartment contained a Pt working electrode, the reference electrode and 5 ml MeCN containing 2 mM RM and 10 mM KClO₄. The reduction compartment contained Ni foam as a counterelectrode with 5 ml of 100 mM 1,4-benzoquinone (sublimed) in MeCN. A K⁺ selective ion-exchange membrane separated the two compartments. RMs were oxidized galvanostatically to 80% of their total capacity. DMFc, TDPA, TMPD, DMPZ, MPT and DPAB were oxidized using 1 equiv. NOBF₄ in MeCN. After 3 h stirring, they were precipitated with cold diethyl ether, filtered and dried under a vacuum at 30 °C for 12 h. F₄BQ is the oxidized form itself.

Measurements of kinetics

Kinetics of mediated superoxide oxidation were measured using UV–Vis spectroscopy using an Avantes AvaSpec-HSC spectrometer with AVALIGHT-DH-S-BAL light source and fibre optics to perform measurements inside the glove box. Pure KO₂ powder was pressed into about 0.5 mm thick pellets using a 7 mm die set and a hand press (PIKE). In a 10-mm quartz cuvette (Hellma), a KO₂ pellet was placed in a polytetrafluoroethylene frame for alignment, followed by a magnetic stirring bar and then the cuvette was sealed with a gas-tight injection lid. RM^ox solution containing 10 mM KClO₄ was then injected using a gas-tight syringe (Hamilton). Consumption of RM^ox was followed except for F₄BQ, in which formation of RM^red was followed (Extended Data Fig. 7). Data and error bars are presented as mean ± s.d. (n ≥ 3). Error bars appear asymmetric on an ln(k) scale. Repetitions mean that each time a new portion of RM^ox was produced by electrochemically oxidizing a portion of RM^red or by dissolving the chemically produced oxidized form. Differences in the magnitude of the error bars among mediators arise from their large chemical diversity and specific reactivities. For example, Fc⁺ and reduced quinones react with O₂, or high-voltage RM^ox shows limited long-term stability in the electrolyte. For the latter, it was checked that degradation was at least several times slower than the oxidation of KO₂.

Kinetics of Li⁺-induced superoxide disproportionation in TEGDME were measured by placing KO₂ powder in a closed reaction vessel equipped with a pressure sensor (Omega, PAA35X) and injecting the Li⁺ electrolyte using a syringe through a septum (Extended Data Fig. 8).

³O₂ yields and 1,270 nm emission measurements

³O₂ yields on mediated superoxide oxidation were measured using mass spectrometry, as detailed previously³⁰. The RM^ox solutions were injected using a gas-tight syringe, and the measurement continued until the O₂ signal ceased. We used the ¹O₂-specific NIR emission at 1,270 nm from the decay of ¹O₂ to ³O₂ to determine ¹O₂ yields and lifetimes as detailed previously³⁰. The signal was recorded from the detector using an oscilloscope (Pico Technology) and at a gain of 820 V (control voltage). Extended Data Fig. 6 shows examples of the recorded signal during mediated oxidation, as well as Li⁺– and H⁺-induced disproportionation.

From oxidation rates to ³O₂ yields and NIR emission intensities

We use the yields of ³O₂/RM^ox and the normalized NIR intensities in Fig. 2b,c to prove that the two kinetic parabolas correspond to ³O₂ and ¹O₂ evolution. To rationalize their assignment, we use a minimal model to calculate expected ³O₂/RM^ox and NIR emission intensities based on formation rates and ¹O₂ decay processes. We considered the following processes: (1) ³O₂ and ¹O₂ formation rates (k₃ and k₁) as given by the two kinetic parabolas in Fig. 2a; (2) physical and reactive ¹O₂ quenching by the solvent; (3) physical and reactive ¹O₂ quenching by the reduced mediators RM^red. Note that the same processes with RM^ox are typically negligible in comparison because of the electron demand of these processes³⁶; and (4) ³O₂ losses (³O₂/RM^ox < 1) resulting from reactive quenching of ¹O₂ with solvent or mediator.

Losses in ³O₂/RM^ox in Fig. 2b result from incomplete physical quenching of ¹O₂ to ³O₂ due to reactions of ¹O₂ with electrolyte or RM. Hence, we start by considering the decay routes. There are multiple decay routes, as shown in Extended Data Fig. 3f, and only a small fraction of the total ¹O₂ can be detected by the NIR emission at 1,270 nm (refs. ^12,37). First, interactions of ¹O₂ with solvent will result in electronic-to-vibrational (e–v) deactivation and reactions with the solvent. The first-order ¹O₂ decay rate constant k_D = k_d,r + k_d is composed of a reactive fraction k_d,r and a non-reactive fraction k_d. Second, electron-rich species, such as reduced mediators, exert charge transfer quenching; however, they may also react with the electrophilic ¹O₂ along pathways depending on the particular chemistry³⁶. The rate constant k_Q = k_q,r + k_q is equally composed of a reactive fraction k_q,r and a non-reactive fraction k_q. Third, radiative decay of ¹O₂ to ³O₂ with the emission of a 1,270 nm photon.

We measured the rate constants k_D and k_Q using the luminescence lifetime. An O₂-saturated solution containing Rose Bengal (absorbance of about 0.1 in a 1 cm fluorescence cuvette) was illuminated using a pulsed Coherent OBIS 561 nm laser. The lifetime (τ) and the decay constant (k = 1/τ) of ¹O₂ were measured using the NIR detector. τ was obtained by fitting the decay profile with exp(–t/τ) (Extended Data Fig. 3a). τ in the absence of a quencher relates to the solvent quenching rate constant k_D. k_Q is obtained by plotting 1/τ against the RM^ox concentration \({c}_{{{\rm{RM}}}^{{\rm{ox}}}}\) (Extended Data Fig. 3b,c). Similar to previously reported quenchers¹², k_Q decreases with \({E}_{{\text{RM}}^{\text{ox}/\text{red}}}^{\circ }\) following a trendline with a slope of about –10^3.5 V⁻¹. The logarithmic dependence of the non-radiative fraction k_q is explicable by the required partial charge transfer from the e^–-rich quencher to the ¹O₂, which makes quenchers with lower redox potentials more efficient¹². We consider that the reactive fraction k_q,r depends similarly on redox potential, given that the addition reactions equally require charge transfer from the substrate to ¹O₂ (refs. ^12,36). The scattering of k_Q around the trendline arises from the large chemical diversity of the used mediators. We used both the trendline and the individual values of k_Q for the prediction of NIR intensities in Fig. 2c. As for the fraction of reactive deactivation, k_d,r/k_D and k_q,r/k_Q, these can be determined from ³O₂ consumption¹², which we do below when simulating values of ³O₂/RM^ox.

The surface area A of the KO₂ powder, needed for the calculations, was determined by analysing optical images (Extended Data Fig. 3d). KO₂ powder was dispersed in TEGDME, sonicated, a drop was placed between a microscope slide and a cover slip and sealed air-tight. Images were acquired with transmitted light on a Nikon Ti2E-01 inverted microscope using a Plan Apo λ 40×/0.95 DIC (Differential Interference Contrast) air PFS (Perfect Focus System) objective lens, resulting in a pixel size of 0.183 μm. The images were analysed using the ilastik pixel classification and object classification workflows (https://www.ilastik.org/), resulting in a histogram of particle sizes (Extended Data Fig. 3e). The surface area was calculated by assuming spherical particles, yielding A = 0.23 ± 0.04 m² g^–1.

As quantification of absolute ¹O₂ yields from NIR emission is not straightforward, we normalized the values. The NIR intensity at time t after bringing KO₂ in contact with RM^ox will be proportional to the ¹O₂ concentration, \({I}_{1,270{\rm{nm}}}(t)\propto {c}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)\). The ¹O₂ formation rate by mediated KO₂ oxidation is \({\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)=A\cdot {k}_{1}\cdot {c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)\), with k₁ being the rate constant as given in Fig. 2a. A is constant because the experiments were performed with a large excess of KO₂ over RM^ox. \({c}_{{{\rm{RM}}}^{{\rm{ox}}}}\) and \({c}_{{{\rm{RM}}}^{{\rm{red}}}}\) are given by \({c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)={c}_{{{\rm{RM}}}^{{\rm{ox}}}}(0)\cdot {{\rm{e}}}^{-{k}_{{\rm{tot}}}\cdot A\cdot t}\) and \({c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)={c}_{{{\rm{RM}}}^{{\rm{ox}}}}(0)-{c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)+\)\({c}_{{{\rm{RM}}}^{{\rm{red}}}}(0)-{\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{q}},{\rm{r}}}(t)\cdot t\), where k_tot = k₁ + k₃. The term \({\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{q}},{\rm{r}}}(t)\) is the rate at which ¹O₂ reacts with RM^red as detailed below. ¹O₂ formation and decay will balance³⁷, which results in the presence of solvent and mediator quenching in \({c}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)={\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)/({k}_{{\rm{d}}}+{k}_{{\rm{Q}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t))\). k_Q is either the measured value for the particular mediator or the trendline in Extended Data Fig. 3c. Finally, analogous to the experiment where we integrate the NIR signal until it ceases, we arrive at the expected NIR emission:

To simulate losses of ³O₂ (³O₂/RM^ox < 1 in Fig. 2b), we used the rate of reactive ¹O₂ decay \({\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{r}}}(t)=({k}_{{\rm{d}},{\rm{r}}}+{k}_{{\rm{q}},{\rm{r}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t))\cdot {c}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)\) to define f_r as the reactive fraction of the total ¹O₂ decay rate

\({\nu }_{{}^{1}{\rm{O}}_{2},{\rm{r}}}(t)\) equals the total mediated ¹O₂ formation rate times f_r: \({\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{r}}}(t)={f}_{{\rm{r}}}\cdot A\cdot {k}_{1}\cdot {c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)\). As some of the RM^red reacts, its loss is accounted for using \({\nu }_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2},{\rm{q}},{\rm{r}}}(t)={k}_{{\rm{q}},{\rm{r}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)\cdot {c}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}}(t)={f}_{{\rm{q}},{\rm{r}}}\,\cdot A\cdot {k}_{1}\cdot {c}_{{{\rm{RM}}}^{{\rm{ox}}}}(t)\), where \({f}_{{\rm{q}},{\rm{r}}}=\,{k}_{{\rm{q}},{\rm{r}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)/({k}_{{\rm{D}}}+{k}_{{\rm{Q}}}\cdot {c}_{{{\rm{RM}}}^{{\rm{red}}}}(t))\). Calculations of f_r, f_q,r and \({c}_{{{\rm{RM}}}^{{\rm{red}}}}(t)\) were iterated until convergence was achieved. Finally, ³O₂ yields are

The fractions of reactive deactivation, k_d,r/k_D and k_q,r/k_Q were obtained by fitting the measured values of ³O₂/RM^ox in Fig. 2b with the simulated ones from equation (5). The simulated ³O₂/RM^ox are plotted as the dashed line in Fig. 2b.

Deviations between simulated and measured values may result from the simplicity of the model. The main simplification is as follows: (1) k_Q was measured in homogeneous solutions of RM^red and the model calculates bulk concentrations \({c}_{{{\rm{RM}}}^{{\rm{ox}}}}\) and \({c}_{{{\rm{RM}}}^{{\rm{red}}}}\), but during the heterogenous KO₂ oxidation, bulk and surface concentrations of RM^ox and RM^red differ. (2) We fitted a common fraction of mediator reactivity (k_q,r/k_Q) for all mediators, causing k_q,r and k_Q to decrease exponentially with growing \({E}_{{\text{RM}}^{\text{ox}/\text{red}}}^{\circ }\). As a trend, this is justified given that both reaction and charge transferquenching require e^– transfer, but individual reactivity will vary because of the large chemical diversity of mediators³⁶. (3) We did not account for quenching by O₂ and \({{\rm{O}}}_{2}^{-}\). (4) Some RMs show further reactivities, which can cause ³O₂ loss: Fc⁺ reacts with O₂ (ref. ³⁸), TDPA gets in contact with O₂ spontaneously oxidized to TDPA⁺ and TDPA²⁺ (ref. ¹⁸), and reduced quinones bind to O₂ (ref. ³⁹).

Proton-induced disproportionation

Six types of buffers were used for proton-induced superoxide disproportionation. Britton–Robinson (BR) buffers were prepared with 0.1 M acetic acid, 0.1 M boric acid and 0.1 M phosphoric acid. NaOH (1 M) and HCl (1 M) were used to adjust the pH. Phosphate-buffered saline (PBS) solution and aqueous PBS powder solution (for pH 7.4) were added and the pH was adjusted using 1 M NaOH or 1 M HCl. Citrate buffers were prepared using citric acid and trisodium citrate dihydrate. To adjust the pH, we varied the concentrations of citric acid and trisodium citrate dihydrate. Acidic buffers of KCl and HCl (pH 1 and 2) were prepared by mixing 0.2 M KCl with 0.2 M HCl and adjusting the volume. Neutral to basic buffers of KH₂PO₄/NaOH (pH 7.1 and 10.8) were prepared by mixing 0.1 M KH₂PO₄ with 0.1 M NaOH and adjusting the volume accordingly. To trap the hydrogen peroxide (H₂O₂) produced, to eliminate the possibility of forming ¹O₂ by peroxoacids⁴⁰, titanium(IV)oxysulfate solution (TiOSO₄, 15 wt% in dilute sulfuric acid), 1 M NaOH was used to adjust the pH of TiOSO₄ solutions to pH 1.2 and 1.55.

Figure 4c shows ¹O₂ yields still increasing when the pH is below 4.8, the pK_a of O₂⁻. KO₂ hydrolysis increases the pH in aqueous media according to KO₂ + H₂O → HO₂ + K⁺ + OH^–. Buffer capacities were selected so that the amount of KO₂ did not significantly affect the resulting pH after the reaction. However, despite the buffers, the local pH at the reaction site will be higher than the average. The importance of buffering for a local pH close to the average is evident in control experiments without a buffer. Even at a pH of 1.5, we could not detect ¹O₂ in an unbuffered H₂SO₄ solution, whereas we could in the buffered one (Extended Data Fig. 6e). Therefore, the ¹O₂ yields in Fig. 4c result from a higher local pH.

Driving forces on superoxide oxidation

Superoxide experiences a broad range of oxidizing conditions to liberate oxygen, but explanations for why and to what extent certain oxidizing redox couples evolve ¹O₂ have been unknown. Extended Data Fig. 4 shows the driving forces for superoxide oxidation with various redox couples. The driving forces are shown in comparison with the Marcus kinetic parabola in ether and acetonitrile solvent from Figs. 1 and 2. Li⁺– and H⁺-induced disproportionation are shown in Figs. 3 and 4. The other examples we discuss in Extended Data Fig. 4 arise from superoxide in contact with CO₂ or organic peroxides, with relevance for energy storage and biology^1,30,41.

Considering CO₂ first, we have previously shown that CO₂ in contact with O₂⁻ yields ¹O₂, but the energetics were unknown³⁰. CO₂ in contact with O₂⁻ is known to form peroxomonocarbonates and peroxodicarbonates by repeated uptake of CO₂ by O₂⁻. Intermediate peroxocarbonate species may be reduced by O₂⁻, which releases O₂ (refs. ^41,42,43,44). However, the O₂ spin state has previously not been considered. Extended Data Fig. 4c shows likely redox couples of oxidized/reduced peroxocarbonate species, but their redox potentials are not established experimentally. A previous study has shown, using density functional theory (DFT), that depending on the cation present and the solvent, the particular peroxocarbonate redox couples that oxidize O₂⁻ to O₂ differ⁴, but likely involve CO₄^•–/CO₄^2–, LiCO₄^•/LiCO₄^–, Li₂C₂O₆/Li₂C₂O₆^– or Li₃C₂O₆/Li₃C₂O₆^–. The calculations have shown reaction energies relative to the O₂⁻/³O₂ between about 1 and 1.4 eV. These driving forces, hence, explain ¹O₂ formation from CO₂ in contact with O₂⁻ (Extended Data Fig. 4b).

¹O₂ formation has been examined for exposure of superoxide to organic peroxides, given their occurrence in biological systems⁴⁵. No reaction was observed with alkyl peroxides, whereas acyl peroxides yielded ¹O₂ (refs. ^45,46); however, this has not been connected with driving forces for superoxide oxidation. Nucleophilic attack of O₂⁻ on acyl peroxides forms an acyl radical and carboxylate (Extended Data Fig. 4d). The potential for the acyl radical/carboxylate redox couple has been reported between 1.5 V and 1.7 V compared with SHE (ref. ²³) (1.95–2.05 V compared with O₂/O₂⁻), which explains ¹O₂ formation according to Extended Data Fig. 4a. Alkyl peroxides (ROOR) such as di-tert-butyl, dicumyl and di-n-butyl peroxide have been reported not to form ¹O₂ (ref. ⁴⁵). This can be understood by ROOR only breaking down to RO^– and RO^• at low potentials (–1.31 V to –1.15 V compared with SHE, that is, –0.86 V to –0.70 V compared with O₂/O₂⁻) (ref. ⁴⁷). The RO^•/RO^– couple (–0.06 V to 0.04 V compared with SHE, that is, 0.39–0.49 V compared with O₂/O₂⁻) could, if formed, oxidize O₂⁻, but not to ¹O₂.

Proton-induced disproportionation that yields low but non-negligible ¹O₂ yields at a high pH of about 11 is consistent with reliable theoretical and experimental works. Using a high-level ab initio method, a previous study¹⁷ found that the reaction HO₂ + O₂⁻ → O₂ + HO₂ can proceed by both the singlet and triplet pathways, with the singlet pathway being only about 0.3 eV endoergic. Equivalent experiments exposing KO₂ to H₂O₂ in toluene found about 0.2% ¹O₂ production, as measured using a chemical trap¹⁴. In this experiment, H₂O₂ was the proton source to first form HO₂ (H₂O₂ + O₂⁻ → HO₂⁻ + HO₂). The conditions in these theoretical and experimental studies correspond to a pH of about 11 (pK_a = 11.7 for H₂O₂), in which the reaction to ¹O₂ is only weakly driven. Conversely, ¹O₂ was not detected with alkyl hydroperoxides ROOH as the proton source (pK_a ≈ 12.6) (ref. ^45,48), a result that insufficient driving forces can now explain.

Relation between \({{\boldsymbol{E}}}_{{\genfrac{}{}{0ex}{}{1}{}{\bf{O}}}_{2}/{{\bf{O}}}_{{\bf{2}}}^{-}}^{\circ }\) and the ¹O₂ fraction

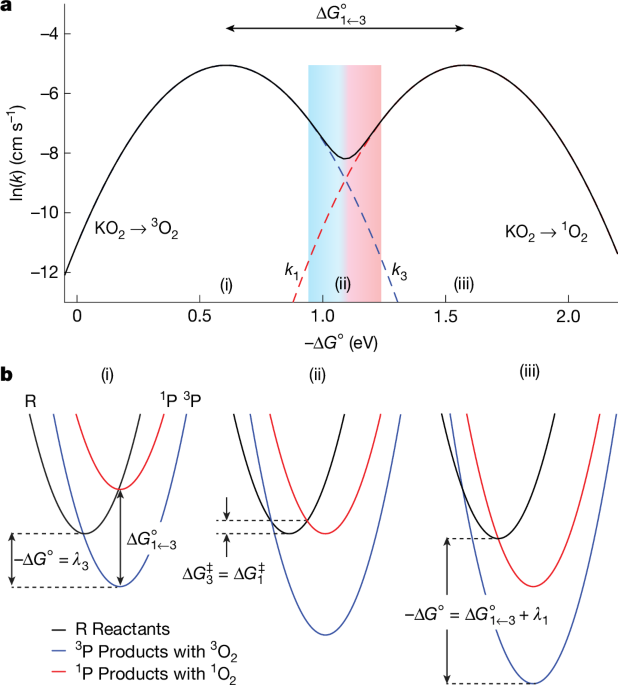
The electrochemiluminescence literature refers to energy-sufficient processes to form the electronically excited species^23,28,49. For example, consider the generic redox couples R/R^•– and M^•+/M (note that these could be, for example, ³O₂/O₂⁻ and RM^ox/RM^red). The process R^•– + M^•+ → ¹R^* + M is considered energy-sufficient to form the excited species ¹R^*, if \(({E}_{{{\rm{M}}}^{\cdot +}/{\rm{M}}}^{\circ }-{E}_{{\rm{R}}/{{\rm{R}}}^{\cdot -}}^{\circ })F\ge \,-\Delta {H}^{\circ }(\,\genfrac{}{}{0ex}{}{1}{}\,{{\rm{R}}}^{* }\leftarrow {\rm{R}})\). This condition is fulfilled if the potential of the oxidizing redox couple exceeds the redox potential of the excited species: \({E}_{{{\rm{M}}}^{\cdot +}/{\rm{M}}}^{\circ }\ge {E}_{\genfrac{}{}{0ex}{}{1}{}{{\rm{R}}}^{* }/{{\rm{R}}}^{\cdot -}}^{\circ }={E}_{{{\rm{R}}/{\rm{R}}}^{\cdot -}}^{\circ }+\Delta {H}^{\circ }(\,\genfrac{}{}{0ex}{}{1}{}\,{{\rm{R}}}^{* }\leftarrow {\rm{R}})/F\). The connotation of energy-sufficient processes led to the interpretation that \({E}_{\genfrac{}{}{0ex}{}{1}{}{{\rm{R}}}^{* }/{{\rm{R}}}^{\cdot -}}^{\circ }\) or \({E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{{\rm{O}}}_{2}^{-}}^{\circ }\) establishes a threshold above which the excited species rather than ground state species forms^18,24,26. Extended Data Fig. 4a shows that reaching this threshold potential (or the driving force for which this is exceeded) gives no indication about the extent to which ¹O₂ rather than ³O₂ forms. An onset of ¹O₂ may be expected at \({\Delta G}_{1\leftarrow 3}^{\circ }\), but its formation will become significant only for driving forces –ΔG° > λ₃, for which ³O₂ formation slows down to benefit ¹O₂ formation.

Thermodynamics in mixed alkali metal/TBA⁺ electrolytes

Superoxide disproportionation in Li⁺ and Na⁺ containing glyme electrolytes was found to always yield some ¹O₂ according to 2MO₂ → M₂O₂ + x³O₂ + (1 − x)¹O₂ (refs. ^13,16,18,19). Li⁺ yielded small fractions (about 2%) at large kinetics, and Na⁺ yielded larger fractions (around 12%) at slow kinetics¹⁶. Often, electrolytes for non-aqueous metal-O₂ batteries contain weakly Lewis acidic cations, such as tetrabutylammonium (TBA⁺) or other cations from ionic liquid electrolytes. In mixed Li⁺/TBA⁺ and Na⁺/TBA⁺ (1/1) electrolytes, the ¹O₂ yields increased to about 20 and 18%, respectively. The reasons for this behaviour must, hence, lie in (1) already sufficient driving forces for ¹O₂ formation in pure Li⁺ and Na⁺ electrolytes; and (2) increasing driving forces on adding TBA⁺.

M₂O₂ (M = Li⁺, Na⁺) are insoluble^50,51 and the potential \({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{M}}}_{2}{{\rm{O}}}_{2}({\rm{s}})}^{\circ }\,=\) \({\Delta }_{{\rm{f}}}{G}^{\circ }({{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})})/F=2.96\,{\rm{V}}\) compared with M⁺/M, therefore, fixed to the value obtained using the formation energy –Δ_fG° of solid Li₂O_2(s). Given that the superoxide/M₂O_2(s) couple acts as the oxidant during superoxide disproportionation, the driving force is given by \(-\Delta G=({E}_{{\rm{superoxide}}/{{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})}}-{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}})F\). Note that here superoxide does not denote a particular species, but it could be anything, including solid MO_2(s), solvated \({({{\rm{M}}}^{+}{{\rm{O}}}_{2}^{-})}_{n\ge 1,({\rm{sln}})}\) clusters and ion pairs, or the weakly coordinated \({({{\rm{TBA}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}\). \({E}_{{\rm{superoxide}}/{\text{M}}_{2}{\text{O}}_{2(\text{s})}}\) cannot be directly measured but can be inferred from \({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})}}\) and \({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}}\). Using ΔG = –zFE, where z is the number of transferred electrons, it can be derived that \({E}_{{\rm{superoxide}}/{{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})}}=2{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{M}}}_{2}{{\rm{O}}}_{2(\text{s})}}-{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}}\). For the stable solid compounds (Li₂O₂, Na₂O₂, NaO₂, K₂O₂ and KO₂), tabulated formation energies Δ_fG° can be found and the \({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{M}}}_{2}{{\rm{O}}}_{2}({\rm{s}})}^{\circ }\) and \({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{M}}{{\rm{O}}}_{2}({\rm{s}})}^{\circ }\) be calculated as shown in Extended Data Fig. 5a. On the basis of this, KO₂ is not expected to disproportionate to K₂O₂ and the K⁺-case, hence, not be further considered.

\({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{superoxide}}}\) require further consideration given the electrolyte-dependent solubilities of superoxide. Theoretical work shows that solvated \({({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{n\ge 1,({\rm{sln}})}\) species are less stable in terms of Gibbs free energy than the bulk solid LiO_2(s), but as the cluster size n grows, the structure approaches bulk MO_2(s) and free energy approaches a constant value^16,50,51. Aggregation into \({({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{n > 1,({\rm{sln}})}\) clusters stabilizes the solvated species relative to separated \({({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}\) species^16,34. The Gibbs free energy grows, therefore, in the order of increasing solvation: LiO_2(s) < (Li⁺O₂^–)_n>1,(sln) < (Li⁺O₂^–)_(sln). Accordingly, the potentials in pure M⁺ electrolyte are in the order and within the limits \({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{{\rm{LiO}}}_{2(\text{s})}} > {E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{n > 1({\rm{sln}})}} > {E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}\). If TBA⁺ is present, the even weaker association in \({({{\rm{TBA}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}\) extends the lower potential limit to \({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{TBA}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}\). The values for these potential limits, as shown in Fig. 3a, Extended Data Fig. 5c,d, were estimated from cyclic voltammograms with the salt shifting from pure M⁺ to pure TBA⁺ (Extended Data Fig. 5b). The largely solvation-independent DMFc/DMFc⁺ redox couple was used as internal standard. Δ_fG° of solid LiO_2(s) is not available, but \({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{\rm{Li}}{{\rm{O}}}_{2}({\rm{s}})}\) may be estimated from cyclic voltammograms in poorly solvating electrolytes, in which large \({({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{n,({\rm{sln}})}\) clusters approach the thermodynamics of LiO_2(s). The shift in the onset of O₂ reduction in Li⁺ compared with TBA⁺ electrolyte at slow scan rates was taken as the difference between \({E}_{{{}^{3}{\rm{O}}}_{2}/{{\rm{LiO}}}_{2(\text{s})}}\) and \({E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{TBA}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}.{E}_{{\genfrac{}{}{0ex}{}{3}{}{\rm{O}}}_{2}/{({{\rm{Li}}}^{+}{{\rm{O}}}_{2}^{-})}_{({\rm{sln}})}}\) as the lower limit of potentials in pure Li⁺ electrolyte was estimated from the potential shift between pure Li⁺ and pure TBA⁺ electrolytes with the highly solvating solvent 1-methylimidazole. These were taken from ref. ³² and show a shift of 33 mV.

Extended Data Fig. 5d shows the analogous thermodynamics for Na⁺/TBA⁺ mixtures as shown in Fig. 3 for Li⁺/TBA⁺. Considerations as above for the relative stabilities of the Li superoxides apply analogously to the relative stability of Na superoxide clusters compared with the NaO_2(s) bulk. Theoretical work has similarly shown the stabilization by forming \({({{\rm{Na}}}^{+}{{{\rm{O}}}_{2}}^{-})}_{n > 1,({\rm{sln}})}\) clusters^52,53. Extended Data Fig. 5e shows the NIR emission on adding KO₂ into glyme electrolyte containing various Na⁺/TBA⁺ ratios. The data show that, even in a pure Na⁺ electrolyte, the driving force is sufficient for ¹O₂ formation and that added TBA⁺ increases the driving force and formation.

More generally, the electrolyte properties (solvent(s), salts(s) and their concentrations) will affect the reorganization energy and hence the maxima and crossing point of the two kinetic parabolas. The classical approach to accounting for this is the equation given by Marcus⁵⁴, which connects the reorganization energy with the effective dielectric properties of the electrolyte and the separation of the redox centres. A lower dielectric constant and smaller separation will result in a larger reorganization energy. A refined equation by Marcus⁵⁵ further takes into account the ionic environment. These considerations apply well, for example, to aqueous anionic redox couples and the series of alkali metal cations from Li⁺ to Cs⁺ as spectator cations, in which λ decreases⁵⁶. However, caution is required with non-aqueous, low dielectric constant media, in which strong ion pairing occurs. Some works suggest an inverse trend for λ among the alkali metals^19,57. Ion pairing and even clustering is particularly severe for (su)peroxide as the redox anions as discussed above. Superoxide forms in non-aqueous Li⁺ and Na⁺ electrolytes clusters^32,33 and the peroxides are practically insoluble⁵¹. The order and extent to which the reorganization energy changes for superoxide oxidation in non-aqueous media among the alkali cations may, therefore, not be predicted straightforwardly and would merit further investigation. As we observe ¹O₂ at low driving force for the Na⁺ electrolyte, the reorganization energy appears sufficiently low therein.

Wider relevance for life sciences and energy

Our study contributes to understanding how the pH affects the link between the four important reactive oxygen species (ROS) superoxide, peroxide, ³O₂ and ¹O₂. Disproportionation is notably the pathway to maintain a low superoxide concentration. However, detoxification from superoxide produces the harmful ¹O₂. Superoxide occurs in cells in several organelles with different pH levels between 4.7 and 8, but the superoxide-degrading enzyme superoxide dismutase occurs only in neutral to basic organelles³⁵. In pathological situations, the pH balance is known to be affected (typically towards lower pH) and therefore signalling, redox regulation and defence^58,59. Our study contributes to the understanding of how the redox chemistry of superoxide, pH and ¹O₂ formation are linked. We noted that in non-aqueous media, superoxide in contact with CO₂ forms ¹O₂. Given the ubiquity of CO₂ in organelles containing superoxide, further investigations into the aqueous chemistry of CO₂ and superoxide are warranted.

For energy applications, further relevance and future research directions emerge: (1) For suppressing ¹O₂, generally, the driving force should be decreased, and the reorganization energy for the superoxide oxidation reaction should be increased. The classical equation by Marcus⁵⁴, which connects the reorganization energy with the effective dielectric properties of the electrolyte and the separation of the redox centres, applies well to aqueous anionic redox couples⁵⁶. For non-aqueous, low dielectric constant media, in which strong ion pairing occurs, particularly so with superoxide, the change in reorganization energy among different cations and electrolytes may not be predicted straightforwardly and would merit further investigation. (2) Oxygen evolution catalysis from water: metal-superoxo species have been identified as preceding the O₂ evolution on, for example, the extensively studied Ni(Fe)OOH or CoOOH catalysts¹⁰. The metal M^n–1/n redox couple is considered to oxidize the superoxo moiety to O₂ (refs. ^10,60). Some of the most active M^n–1/n metal redox couples are typically a few 100 mV above the ¹O₂/superoxide potential shown in Fig. 4a and provide, in principle, enough driving force for ¹O₂ evolution. For example, at pH 14 \({E}_{{\genfrac{}{}{0ex}{}{1}{}{\rm{O}}}_{2}/{{{\rm{O}}}_{2}}^{-}}^{\circ }=1.32\,{\rm{V}}\), \({E}_{{{\rm{Co}}}^{{\rm{II}}/{\rm{III}}}}^{\circ }\approx 1.25\,{\rm{V}}\), \({E}_{{{\rm{Co}}}^{{\rm{III}}/{\rm{IV}}}}^{\circ }\approx 1.5\,{\rm{V}}\), \({E}_{{{\rm{Ni}}}^{{\rm{II}}/{\rm{III}}}}^{\circ }\approx 1.52\,{\rm{V}}\) and \({E}_{{{\rm{Ni}}}^{{\rm{III}}/{\rm{IV}}}}^{\circ }\approx 1.6\,{\rm{V}}\) on the RHE scale (refs. ^10,60). Further investigations specifically on ¹O₂ evolution in oxygen evolution catalysis are therefore warranted. (3) Both Li-stoichiometric⁶ and Li-rich transition metal (TM, for example, Ni, Mn and Co) oxide^2,7,61,62 intercalation materials used for positive electrodes in Li- or Na-ion batteries are known to undergo parasitic lattice oxygen loss at high states of charge. Both the intercalation material and the electrolyte degrade, hampering long-term cyclability. However, non-matching patterns of O₂ and CO₂/CO release from electrolyte decomposition (all containing lattice O as shown by isotopic labelling^7,62) and enhanced lattice O loss with surface carbonates present⁷ remain unexplained and highlight the need for a deeper understanding of the prevailing ROS and decomposition pathways. For LiNiO₂, ¹O₂ evolution has been suggested to result from the disproportionation of oxide radicals⁶. More generally, ¹O₂ may evolve from superoxo species (at the lattice surface, in (su)peroxocarbonates^4,30) at the available driving forces. The oxidants could be a combination of (su)peroxides (for example, coordinated by TMs or carbonates) that get stabilized by further reduction and TM redox, such as Co^III/IV or Ni^III/IV. Further investigations into the involvement of ¹O₂ evolution in TM oxide outgassing and surface reactions are therefore warranted.

The results expand the current knowledge on the electrogeneration of excited species more generally and pose open questions about the origin. Specifically, the process is more effective than typically assumed, given that \({\Delta G}_{1\leftarrow 3}^{\circ } < {\Delta H}_{1\leftarrow 3}^{\circ }\) and that Z_el,1 ≫ Z_el,3. Electrogeneration of excited ROS has significance ranging from biological systems to energy storage. Reactive excited species in life are very broadly associated with pathogenic events^1,63. Recombination reactions in redox flow batteries are recognized to cause self-discharge, but this has so far not been recognized to potentially form extremely energetic excited species. Soluble parasitic oxidized and reduced species at the cathode and anode of Li- and Na-ion batteries may recombine to form energetic excited species.