Design of facilitated dissociation enables timing of cytokine signalling

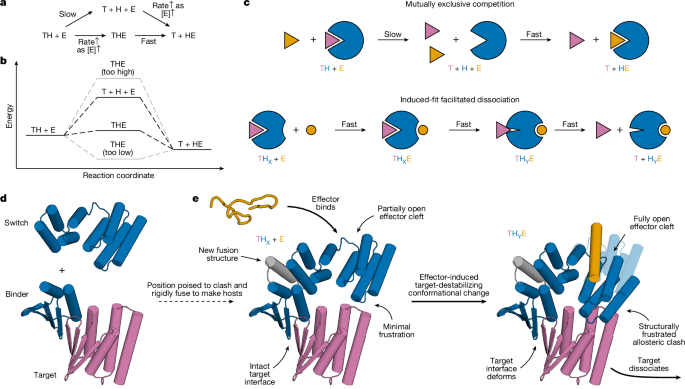
Design of structured switch–binder fusions (hosts) allosterically coupling the target and the effector

In PyMOL, we manually positioned the switch relative to the binder–target complex subject to several constraints: there is no steric overlap between the target and switch state X; there is large steric overlap between the target and switch state Y; the smallest deformation that could be undergone by the switch and the target to resolve this clash is in the desired direction; and the switch C terminus and binder N terminus are relatively oriented such that sensible additional structure could be built between the switch and the binder to rigidly fuse them as positioned. To aid in visualizing this additional structure, we also included placeholder helices while manually positioning the switch and binder, effectively ‘sketching’ the fusion (Supplementary Fig. 4b).

We then refined these sketches into plausible backbones. For the initial fusions including AS0, we extracted the centre four residues of the placeholder helix, then used inpainting with RosettaFold⁵⁶ to scaffold that fragment between the switch and the binder. For later fusions, including the AS1 variants and ASNeo2 designs, we first used Rosetta FastDesign⁵⁷ to sample around the starting sketch for designable positions of the switch, binder and placeholder helices while keeping the region of the state X switch that clashes in state Y fixed relative to the target, then used RFDiffusion⁷ (conditioned on the secondary structure and block adjacency of the sketches) to build structure between the sampled switch and binder positions. During both structure-generation approaches, we masked noncritical residues on the switch and binder interfacing with the fusion structure. After generation of the fusion backbone structure, we used ProteinMPNN⁵⁸ to optimize sequences for the fusion structure and the masked residues on the switch and binder. To filter designs, we used AF2⁵⁹ (with initial guess (AF2-IG)⁶⁰ for complex predictions) to predict the structure of the fusions alone, with the target, and with the effector, selecting designs for which each structural state is correctly and confidently predicted by a majority of the five model weight sets. Finally, for the AS1 variants and ASNeo2 designs, we used AF2-IG to predict the structure of the strained ternary complexes, selecting sets with a diversity of deformation directions.

Design of induced-fit register-shift switches

Designs AS1, AS2, AS5 and AS7 were generated starting from design AS0, which contains the hinge switch cs221. When cs221 was designed, its state Y was generated by copying the N-terminal domain (helices 1–4) of its parent scaffold (DHR20; ref. ⁶¹), aligning helix 4 of the copy to the corresponding helix of DHR20 offset by three residues, and combining the transformed N-terminal domain and original C-terminal domain into a single protein³³. Thus, relative to the C-terminal domain, the N-terminal domain is both rotated around and translated along the axis of helix 4, exposing a cleft between the domains for binding a helical peptide. Now, to generate a new state X for this switch that retains an open cleft, we repeated this procedure but aligned the N-terminal domain with a residue offset of −4 instead of 3, so that overall this position of the N-terminal domain is shifted from state Y along helix 4 by one heptad (Supplementary Fig. 4e). This introduces minimal rotation and thus maintains the open cleft. We combined this new position of the N-terminal domain with the entire C-terminal domain of AS0 (including the fusion to LHD101B), then used Rosetta FastDesign to further sample designable positions of the N-terminal domain around this starting point. In half of the design trajectories, we included a placeholder helix in the cleft to help ensure it remains open. We then used inpainting with RosettaFold to generate loops connecting the domains, then paired these complete state X backbones with the original effector-bound state Y of AS0 (also generating new loops between domains in state Y as necessary to match the loop lengths of each new state X).

To generate single sequences that support both states, we first performed multi-state design with Rosetta FastDesign (enforcing sequence symmetry between states) to further refine the paired backbones so that they are more mutually compatible, then used ProteinMPNN with residue probabilities tied at corresponding positions between states to optimize sequences simultaneously for both conformations³³. During these sequence-design steps, the sequence of the effector and of the binder fusion was kept fixed. To filter designs, we used AF2-IG to predict the structure of the switches both with and without the effector, selecting designs for which the new state X (in the absence of effector) and state Y (in the presence of effector) are correctly and confidently predicted by a majority of the five model weight sets. To further ensure that these designs favour state X in the absence of effector and state Y in the presence of effector, we only selected designs that scored more favourably in Rosetta in state X than in state Y, but also scored more favourably in state Y with the effector bound than the sum of the scores of state X and the unbound effector.

Design of rapid sensors

We first sought to cage the SmBiT peptide within the effector so that, through reverse facilitated dissociation, binding of the target would rapidly uncage the SmBiT to enable luciferase reconstitution. We grafted SmBiT onto the effector peptide at a range of positions, then screened these ‘SmBiTgraft’ variants for binding to AS0 and rapid dissociation after binding of the target. We used AS0 as the base design, reasoning that its closed state X would slow undesired peptide reassociation. For each working SmBiTgraft, we then generated a flexibly linked LgBiT–SmBiTgraft–AS0 construct. The best construct shows low luciferase activity that increases rapidly after addition of target, but only slowly after addition of effector peptide (which must compete directly with SmBiTgraft) (Extended Data Fig. 6). To demonstrate the modularity of this platform, using the methods described above for designing hosts, we rigidly fused a SARS-CoV-2 RBD binder (LCB1; ref. ⁴³) to the switch in place of the target binder such that the RBD clashes with the switch in state Y but not in state X, and tested 16 of these AScov fusion designs.

Recombinant expression and purification

Synthetic DNA fragments encoding each design were obtained from IDT as eBlocks and cloned into custom vectors using Golden Gate assembly⁶². Designs usually contained a C-terminal sequence-specific nickel-assisted cleavage (SNAC) tag⁶³ and a 6×His tag (MSG-Protein-GSGSHHWGSTHHHHHH). Proteins to be captured on the chip for SPR experiments contained an N-terminal AviTag and a C-terminal 6×His tag (MSGLNDIFEAQKIEWHESSG-Protein-GSGHHHHHH). For the size-exclusion chromatography (SEC) binding experiments shown in Supplementary Fig. 6 and for screening SmBiTgraft effector peptide variants with SPR, the effector was fused to superfolder GFP in a sfGFP-GSSG-Effector-GSHHHHHH construct. To rapidly break split luciferases, AS1 was fused to LgBiT in a MSG-AS1-linker-LgBiT-GSHHHHHH construct and the target was fused to SmBiT in a MSG-Target-linker-SmBiT-GSHHHHHH construct. In the rapid sensors, AS0 and AScov were fused to LgBiT and a SmBiT-containing effector in a MSGHHHHHHGS-LgBiT-linker-SmBiTgraft-linker-(AS0 or AScov)-GS construct. Sequences for all designs are available in Supplementary Table 4.

All proteins were expressed from NEB BL21(DE3) E. coli cells using TBII (MpBio) autoinduction medium with 0.5% (w/v) glycerol, 0.05% (w/v) glucose, 0.2% (w/v) lactose, 20 mM MgSO₄, trace metal mix and 50 μg ml⁻¹ kanamycin. Expression cultures (50 ml) were grown either at 37 °C for 16–20 h or at 37 °C for 6–8 h, then at 18 °C for 16–20 h. Cells were collected by centrifugation, resuspended in 5 ml lysis buffer (100 mM Tris HCl pH 8.0, 200 mM NaCl, 50 mM imidazole, 1 mM PMSF, and 1 Pierce Protease Inhibitor Mini Tablets, EDTA-free per 50 ml) and lysed by sonication. The lysate was clarified by centrifugation at 14,000g for 30 min. Protein in the soluble lysate was bound to 1 ml Ni-NTA resin (QIAGEN), washed with 5 ml low-salt wash buffer (20 mM Tris HCl pH 8.0, 200 mM NaCl and 50 mM imidazole), 5 ml high-salt wash buffer (20 mM Tris HCl pH 8.0, 1 M NaCl, 50 mM imidazole) and 5 ml low-salt wash buffer, and eluted in 1.2 ml elution buffer (20 mM Tris HCl pH 8.0, 200 mM NaCl and 500 mM imidazole) after a 0.4 ml pre-elution. The proteins were further purified by SEC on a fast protein liquid chromatography (FPLC) system with a Superdex 200 Increase 10/300 GL column in Tris-buffered saline (TBS; 20 mM Tris pH 8.0 and 100 mM NaCl) with 1-ml fractions. Where possible, fractions that probably corresponded to protein monomers were selected. Final protein concentrations were estimated using molar extinction coefficients predicted from the protein sequence and integrating the absorbance at 280 nm over the selected fractions. Correct protein molecular weights were confirmed using liquid chromatography–mass spectrometry (LC–MS).

Peptide synthesis

The effector peptide cs221B was chemically synthesized by GenScript. The TAMRA-labelled effector used in fluorescence polarization (FP) experiments was synthesized as previously described³³.

SEC binding assay

Individual host proteins, sfGFP–effector and 1:1 host:sfGFP–effector mixtures were prepared at 20 μM in TBS (20 mM Tris pH 8.0 and 100 mM NaCl). A 0.5-ml quantity of each solution was injected onto a Superdex 200 Increase 10/300 GL column in TBS and the absorbance at 230 nm was monitored for changes in the retention volumes of the mixture compared with the individual proteins.

Fluorescence polarization

FP binding experiments with TAMRA-labelled effector were performed at 25 °C in TBS (20 mM Tris pH 8.0 and 100 mM NaCl) with 0.05% v/v TWEEN20 in 96-well plates (Corning 3686). Parallel and perpendicular fluorescence intensity was measured using a Synergy Neo2 plate reader with an FP 530/590 filter cube. Fluorescence polarization P (in units of mP) was calculated by the following expression:

For affinity measurements, host proteins were titrated by twofold serial dilution across TAMRA–effector (at a constant concentration between 0.1 and 1 nM) through 24 wells, with a final volume of 80 μl in each well. Plates were incubated for at least 12 h at room temperature to fully equilibrate before measurement. To determine affinities, the following binding isotherm function was fitted to the measured polarization values using nonlinear least-squares minimization:

where P is the modelled polarization, P₀ is the polarization of free effector, P₁ is the change in polarization after binding the host, f_bound is the fraction of effector bound to the host, [H] and [E] are the total concentrations of host and effector, respectively, and K_d is the affinity between the host and the effector. When the fit K_d is lower than [E], affinities are too strong to be accurately measured with this method, so ‘K_d < [E]’ is reported.

For kinetic competition measurements, the target LHD101An1 was titrated by twofold serial dilution across the host protein (at a constant concentration of 22 nM) through five wells (a sixth well with just the host was also included) with a final volume of 72 μl in each well. Plates were incubated for one hour to allow the host and the target to equilibrate. To each well, 8 μl of 200 nM TAMRA–effector was added and rapidly mixed using a multichannel pipette, and the measurement was started immediately afterwards. This resulted in a 20 nM final concentration of both host and effector in a final volume of 80 μl per well. The following single exponential decay function was fitted to the measured polarization time courses using nonlinear least-squares minimization:

where P is the modelled polarization, P₀ is the polarization of free effector, P₁ is the amplitude of the change in polarization, k_app is the apparent rate constant and t is the time after the start of the measurement.

To measure facilitated dissociation in the reverse direction, host and TAMRA–effector were incubated at a 2:1 ratio to fully saturate the effector with host, diluted to 4 nM host and 2 nM effector, and distributed across 11 wells (40 μl in each well). In nine separate wells, the target was titrated by a fourfold serial dilution with constant excess unlabelled effector (40 μM). Just excess unlabelled effector at 40 μM was prepared in the 10th separate well (to measure the base rate of effector dissociation), and buffer was prepared in the 11th (to confirm the baseline remains stable). Forty microlitres of these target + effector solutions were added to the 11 host + TAMRA–effector wells and rapidly mixed using a multichannel pipette, and the measurement was started immediately afterwards. This resulted in final concentrations of 2 nM host, 1 nM TAMRA–effector, 20 μM unlabelled effector (to make the dissociation of TAMRA–effector irreversible) and varying concentrations of target in a final volume of 80 μl per well. The following single exponential decay function was fitted to the measured polarization time courses using nonlinear least-squares minimization:

The following hyperbolic function was fitted to the apparent rate constants k_app:

where k_off,H:E is the base effector off-rate constant, k_off,TH:E is the off-rate constant for accelerated effector dissociation from the ternary complex, K_1/2 is the concentration at which half the rate increase from k_off,H:E to k_off,TH:E is reached and [T] is the concentration of target present.

SPR

Proteins to be captured on the SPR chip were expressed with an N-terminal AviTag and purified as described above, except that the proteins were biotinylated after elution from the Ni-NTA resin: to the elutions, 5 μg ml⁻¹ BirA (Avidity), 10 mM ATP, 10 mM Mg(OAc)₂ and 100 μM d-biotin were added and allowed to incubate at room temperature for at least 4 h before further purification by SEC. Successful biotinylation was confirmed using LC–MS. SPR measurements were performed at 25 °C in HBS-EP+ buffer (Cytiva) on a Biacore 8K instrument. Biotinylated proteins were immobilized on the chip using the Biotin CAPture system (Cytiva).

For measurements of target off-rate constants, biotinylated target protein was immobilized on the chip. To measure base off-rate constants k_off,T:H, host proteins at 50 nM were flowed over the chip for 60 s, then dissociation was measured for 2 h. To measure accelerated off-rate constants k_off,T:HE, pre-incubated host–effector complexes (host at 1 μM and effector at 5 μM to ensure that the host is saturated with effector) were flowed for 60 s to form the ternary complex on the chip, then dissociation was measured for 4–20 min under a constant flow of 5 μM effector. Most dissociation data were fitted with the following double exponential decay function to account for populations of host protein with different dissociation kinetics:

where S is the modelled SPR response, S₀ is the baseline, S₁ and S₂ are amplitudes relating to the sizes of each host population, k_app,1 and k_app,2 are apparent rate constants corresponding to each host population, t is the time and t₀ is the time at which dissociation initiates. The reported rate constant typically corresponds to the faster and higher amplitude exponential in the fit; instances in which other criteria are used to determine which rate constant corresponds to the change of interest are noted. When clearly only one host population is present (often indicated by k_app,1 ≈ k_app,2 or a large difference between S₁ and S₂ when fitting a double exponential), the following single exponential decay function was fitted instead, in which the parameters are the same as above (instances in which single exponentials were used are noted):

To measure the rate constant of effector association to form the ternary complex, biotinylated host protein was immobilized on the chip. The host protein was saturated with target by flowing 5 μM target over the chip for 4 min, then a varying concentration of effector and 5 μM target was flowed over the chip for 2–4 min to associate the effector, and finally 5 μM target was flowed over the chip for 4 min to monitor effector dissociation. Target was included at 5 μM (higher than its affinity to the ternary complex) throughout the experiment to ensure that the host remained saturated with target, preventing changes in target binding from convoluting the response from effector binding. Association data were fitted with the following single exponential decay function:

where S is the modelled SPR response, S₀ is the baseline, S₁ is the amplitude, k_app is the apparent rate constant, t is the time and t₀ is the time at which dissociation initiates.

With the peptide effector, the following linear function was fitted to the apparent rate constants:

where k_on,TH:E and k_off,TH:E are on-rate and off-rate constants and [E] is the concentration of effector flowed over the chip.

With the 3hb effector, the following hyperbolic function was fitted to the apparent rate constants:

where k_switch is the rate constant for the TH_X → TH_Y conformational change, k_unswitch is the rate constant for the TH_Y → TH_X conformational change, k_on,TH:E and k_off,TH:E are on-rate and off-rate constants and [E] is the concentration of effector flowed over the chip. This function describes the slow relaxation rate constant of binding by conformational selection⁶⁴. The data can be fitted with only the slow relaxation because, as the conformational pre-equilibrium favours state X (that is, k_switch « k_unswitch), the effect of the fast relaxation on k_app is minimal. During the fit, k_off,TH:E was constrained to a low value (<1 × 10⁻⁴ s⁻¹), as observed.

To measure the effector-concentration-dependent rate constant of the full facilitated dissociation process, either biotinylated target protein or biotinylated common gamma γ_c ectodomain (Acro Biosystems ILG-H85E8) was immobilized on the chip. For experiments with ASNeo2 designs, the ASNeo2 hosts were pre-incubated with IL-2Rβ ectodomain (Acro Biosystems CD2-H5221) before association with γ_c. Each experiment involved multiple cycles of host association and induced dissociation under the flow of various concentrations of effector obtained by twofold serial dilution (Supplementary Fig. 8a). Throughout these cycles, a small population of host that is unresponsive to the effector (‘Hn’, owing to partial degradation or misfolding induced by the strain in the ternary complex) could accumulate on the chip (Supplementary Fig. 8a,b). The following system of differential equations describing the expected behaviour of the proteins on the chip (accounting for this accumulation) can be fitted to the dissociation curve of cycle n (Supplementary Fig. 8c):

with initial values computed for each cycle by

and the modelled concentrations of each complex state on the chip is related to the SPR response by

where S is the modelled SPR response, [THE], [TH] and [THn] are concentrations of complex states on the chip, t is the time after the start of the dissociation cycle, [E] is the concentration of effector flowed over the chip, k_off,T:H, k_off,T:HE, k_on,TH:E, k_off,TH:E and k_off,T:Hn are on-rate and off-rate constants, a_TH, a_THE and a_THn are amplitudes relating the concentration of each state on the chip to an SPR response, f_n is an amplitude fudge factor for cycle n accounting for small differences in amplitude across cycles and f_responsive is the fraction of host that is responsive to the effector. Varying all of these parameters, this model is then globally fitted to the dissociation curves of all cycles using nonlinear least-squares minimization. Note that with a sufficiently high value of k_on,TH:E, this model’s dissociation kinetics are determined mainly by the target dissociation parameters k_off,T:H and k_off,T:HE; meanwhile, the effector binding parameters k_on,TH:E and k_off,TH:E tend to tightly covary and cannot be accurately determined from these fits. Also note that for designs with low values for k_off,T:HE, this model may be less accurate because the assumption that [THE] = 0 at the beginning of each cycle may no longer be valid. To compute the effective rate constant of the full facilitated dissociation process for intact host, we used the following simplified system of differential equations, which no longer accounts for a small population of unresponsive host:

For each effector concentration [E], this system was solved for the half-time of the target:host interaction t_1/2 using the rate parameters determined from the original model fitted to the data, and the effective rate constant of the full dissociation process k_eff was computed from each half-time as follows:

The following hyperbolic function was fitted to the effective rate constants (constrained to the values of k_off,T:HE and k_off,T:H obtained from the global fit):

where k_off,T:H is the base target off-rate constant, k_off,T:HE is the off-rate constant for accelerated target dissociation from the ternary complex, K_1/2 is the concentration at which half the rate increase from k_off,T:H to k_off,T:HE is reached and [E] is the concentration of effector flowed over the chip.

The discrepancy in the 3hb EC₅₀ between the 3hb association experiment in Fig. 2f (right) and the target facilitated dissociation experiment in Fig. 2h (right) could result from the fusion tag that was used to fix AS1 to the surface competing with the 3hb for binding the cleft, reducing the apparent 3hb on-rate in the 3hb association experiment but not in the target facilitated dissociation experiment.

All SPR measurements in the main figures were repeated at least once, with similar results.

Circular dichroism spectroscopy

Circular dichroism spectra were measured at 25 °C on protein samples at 0.2 mg ml⁻¹ in TBS (20 mM Tris pH 8.0, 100 mM NaCl) using a Jasco J-1500 spectrophotometer.

X-ray crystallography

The AS1 TH and THE complexes required increased hydrophobicity to crystallize. This was accomplished by lysine methylation (for crystals AS1_TH 1, AS1_TH 2 and AS1_THE 1) or with the hydrophobic surface mutations K46L, E50W, K172W and E173Y (for crystal AS1_THE 2).

Protein was expressed from NEB BL21(DE3) E. coli cells using TBII autoinduction medium as above but at a larger scale: either 8 × 50 ml or 1–2 × 500 ml cultures. Cells were collected by centrifugation, resuspended in lysis buffer and lysed by sonication. The lysate was clarified by centrifugation at 14,000g for 30 min. Protein in the soluble lysate was bound to 8 ml Ni-NTA resin (QIAGEN), washed with 10 ml low-salt wash buffer, 30 ml high-salt wash buffer and 10 ml SNAC cleavage buffer (100 mM 2-(N-cyclohexylamino)ethanesulfonic acid (CHES), 100 mM acetone oxime, 100 mM NaCl and 500 mM guanidinium chloride, pH 8.6)⁶³ and incubated in 40 ml SNAC cleavage buffer + 2 nM NiCl₂ for 12 h at room temperature to cleave. Afterwards, the flowthrough was collected and the beads were washed with 40 ml lysis buffer (minus the protease inhibitors). The amount of cleaved protein in the flowthrough and wash was assessed with SDS–PAGE, and fractions with enough cleaved protein were concentrated and further purified using SEC on an FPLC system with either a Superdex 75 Increase 10/300 GL column or a HiLoad 20/600 Superdex 75 pg column in either TBS (20 mM Tris pH 8.0 and 100 mM NaCl) or lysine methylation buffer (50 mM HEPES pH 7.5 and 250 mM NaCl) if lysine residues in the protein were to be methylated. For protein complex cocrystallization, the purified proteins and/or chemically synthesized effector were mixed at equimolar ratios. For some samples (resulting in crystals AS1_TH 1, AS1_TH 2 and AS1_THE 1), lysine residues were methylated as previously described⁶⁵, and the reaction was quenched using SEC on an FPLC system to buffer-exchange into TBS. Finally, the samples were concentrated to crystallization levels.

Crystallization experiments were done using the sitting drop vapour diffusion method. Initial crystallization trials were set up in 200-nl drops using the 96-well plate format at 20 °C. Crystallization plates were set up using a Mosquito LCP from SPT Labtech, then imaged using UVEX microscopes and UVEX PS-256 from JAN Scientific. Diffraction-quality crystals formed in 0.2 M magnesium chloride hexahydrate, 0.1 M sodium cacodylate pH 6.5 and 50% v/v PEG 200 for AS1_H; in 0.2 M sodium chloride, 0.1 M Na/K phosphate pH 6.2 and 50% v/v PEG 200 for CS221B; in 0.1 M sodium acetate pH 5.0, 5% w/v γ-PGA (Na⁺ form, LM) and 30% v/v PEG 400 for LHD101An1; in 0.2 M magnesium chloride hexahydrate, 0.1 M Tris pH 8.5 and 25% w/v polyethylene glycol 3,350 for AS5_HE; in 0.1 M sodium acetate pH 5.0 and 20% (v/v) MPD for AS5_H; in 0.2 M 1,6-hexanediol, 0.2 M 1-butanol, 0.2 M 1,2-propanediol, 0.2 M 2-propanol, 0.2 M 1,4-butanediol, 0.2 M 1,3-propanediol, sodium HEPES, MOPS (acid) pH 7.5, 40% v/v PEG 500 MME and 20% w/v PEG 20000 for AS1_HE; in 0.1 M citric acid pH 3.5 and 2.0 M ammonium sulfate for AS1_THE 1; in 1.0 M lithium chloride, 0.1 M citrate pH 4.0 and 20% w/v PEG 6000 for AS1_THE 2; in 2.4 M sodium malonate pH 7.0 for AS1_TH 1 (P 6₁ 2 2); and in 1.8 M ammonium citrate tribasic pH 7.0 for AS1_TH 2 (P 2₁ 2₁ 2₁).

Diffraction data were collected at the National Synchrotron Light Source II beamline 17-ID-1 (FMX/AMX), the Advanced Light Source beamline 821/822 or the Advanced Photon Source NECAT 24ID-C. X-ray intensities and data reduction were evaluated and integrated using XDS⁶⁶ and merged and scaled using Pointless or Aimless in the CCP4 program suite⁶⁷. Structure determination and refinement starting phases were obtained by molecular replacement with Phaser⁶⁸, using the designed model for the structures. After molecular replacement, the models were improved using phenix.autobuild with rebuild-in-place to false and using simulated annealing. Structures were refined in PHENIX⁶⁹. Model building was performed using Coot⁷⁰. The final model was evaluated using MolProbity⁷¹. Data collection and refinement statistics are provided in Extended Data Tables 1–3.

DEER spectroscopy

Spin-label modelling and distance distribution predictions were performed as previously described³³ using chiLife⁷² with the off-rotamer sampling method⁷³. Site pair selections were performed as previously described³³. Host protein variants containing cysteine residues at the selected sites were purified as described above, except that 0.5 mM TCEP was included in the lysis buffer and the first two Ni-NTA resin washes, and the proteins were labelled immediately after elution from the Ni-NTA resin: to the elutions, 50 μl of 200 mM of the nitroxide spin label 1-oxyl-2,2,5,5-tetramethyl-3-pyrroline-3-methyl)methanethiosulfonate (MTSL) in dimethyl sulfoxide (DMSO) was added and allowed to incubate for at least 2 h at room temperature before further purification by SEC. Successful labelling was confirmed using LC–MS. DEER samples were prepared at 20 µM labelled host protein in deuterated solvent buffered by 20 mM Tris at pH 8.0 with 100 mM NaCl and 20% d₈-glycerol (Cambridge Isotope Laboratories) as a glassing agent. When appropriate, target and effector were added to a concentration of 100 µM each. Then, 15–30 µl of each sample was loaded into a quartz capillary (Sutter Instrument, 1.1 mm inner diameter, 1.5 mm outer diameter) and flash-frozen with liquid nitrogen. Samples were stored at −80 °C until the DEER experiments were performed.

DEER experiments were performed as previously described³³. An ELEXSYS E580 spectrometer (Bruker) at Q-band (around 34 GHz) with an EN5107D2 resonator (Bruker) was used for all experiments. The temperature was maintained at 50 K using a cryogen-free cooling system (ColdEdge). The four-pulse DEER sequence was used, using 60-ns Gaussian observer pulses with a full width at half maximum (FWHM) of 30 ns and a frequency near the centre of the field-swept spectrum and 150-ns sech/tanh probe pulses with centre 80 MHz above the observer frequency, 80 MHz bandwidth and a truncation parameter of 10. All shaped pulses were generated using the SpinJet arbitrary waveform generator (Bruker). Pulse shapes were calculated using PulseShape (https://github.com/stolllab/PulseShape), using both resonator compensation and transmitter nonlinearity compensation. All data were collected using a 2 ms shot repetition time, 8-step phase cycling and τ₁ averaging from 400 ns to 528 ns in 16-ns steps. All other experimental parameters (including pump pulse time step, τ₂ delays, number of scans and others) were chosen on a per-sample basis and are reported in Supplementary Table 3.

All DEER data were analysed using the DeerExp module of the eprTools Python package (https://github.com/mtessmer/eprTools). All data were fitted using separable nonlinear least squares⁷⁴. The foreground signal was modelled using Tikhonov regularization with the second derivative operator. The regularization parameter was selected using generalized cross-validation. The background was modelled using a 3D-homogeneous spin distribution. An additional penalty restraining the modulation depth to be low was used to prevent the fitting of long-distance artefacts in the foreground, as was done previously⁷⁵. Confidence intervals were estimated using bootstrap sampling with 100 samples using a fixed regularization parameter. Fit parameters such as the regularization parameter, the modulation depth and the signal-to-noise ratio are listed in Supplementary Table 3.

MD simulations

Input files for the MD simulation were prepared with CHARMM-GUI^76,77, with AF2 structure as the initial structure. A rectangular water box of edge length 10 Å was placed around the protein. The water box contained potassium and chlorine ions of concentration 0.15 M that neutralized the protein’s net charge. The ions were placed in the water box using the Monte Carlo method. To model the system, the CHARMM36m force field⁷⁸ was used. After the explicit solvent system was made, the system was minimized and equilibrated before the production MD run. All three steps were performed with the GROMACS 2020.2 MD engine^79,80.

The steepest descent method was used for energy minimization, for 5,000 steps with an energy tolerance of 1000 kJ mol⁻¹ nm⁻¹. The neighbour list was updated every ten steps with a cut-off distance of 1.2 nm. Cut-off was used to calculate Van der Waals interactions with a switch distance of 1.0 nm and a cut-off distance of 1.2 nm. The force was smoothly switched off between the switch distance and the cut-off distance. The fast smooth particle-mesh Ewald method was used to calculate electrostatics with a cut-off distance of 1.0 nm. All bonds with hydrogen atoms were treated as rigid using the linear constraint solver (LINCS) algorithm⁸¹.

The equilibration step was performed with a leap-frog algorithm using a time step of 1 fs and a total simulation time of 125 ps. The system was propagated in the NVT ensemble. The temperature was maintained at 303.15 K using the velocity rescaling method. The solute and solvent were coupled with a time constant for coupling of 1 ps. The centre-of-mass translational velocity was removed every 100 steps to prevent the system from drifting. The cut-off schemes for Van der Waals and electrostatic interactions were the same as those used in the minimization step, except that the neighbour list was updated every 20 steps. The velocities were generated from a Maxwell distribution with a temperature of 303.15 K. The same LINCS method was used to constrain the hydrogen atoms during the equilibration step.

The production step was performed with a leap-frog algorithm using a time step of 2 fs and a total simulation time of 1 μs. The trajectories with the same initial equilibrated structure were obtained in triplicate. The system was propagated in the NPT ensemble. The temperature was maintained at 303.15 K using the velocity rescaling method. The solute and solvent were coupled with a time constant of 1 ps. Exponential relaxation pressure coupling and isotropic coupling with a time constant of 5.0 ps was used to maintain the pressure at 1.0 bar. The cut-off schemes for Van der Waals and electrostatic interactions were the same as those used in the minimization step, except that the neighbour list was updated every 20 steps and the Coulomb cut-off distance was set as 1.2 nm. The centre-of-mass velocity removal was the same as that used in the equilibration step. The same LINCS method was used to constrain the hydrogen atoms during the production step.

Analysis of the trajectories, such as RMSD and root mean square fluctuation (RMSF) calculations, was performed with MDAnalysis⁸². To simulate DEER distance distributions from these trajectories, structures along each trajectory were clustered using the Gromos clustering algorithm⁸³ in GROMACS, distance distributions were predicted (using chiLife⁷² with the off-rotamer sampling method⁷³) for the centre structure of each cluster and the resulting distributions were averaged weighted by the occupancies of their corresponding clusters.

Chain reactions with FRET readout

Hinge protein cs201F_E249L (H2) was purified as described above, except that 0.5 mM TCEP was included in the lysis, wash and elution buffers, and the SEC buffer was phosphate-buffered saline (PBS; 20 mM sodium phosphate pH 7.0, 100 mM NaCl and 0.5 mM TCEP). To double label with dyes, 50 μM H2 was incubated with 250 μM Alexa Fluor 555 C₂ maleimide (donor; Thermo Fisher Scientific) and 250 μM Alexa Fluor 647 C₂ maleimide (acceptor; Thermo Fisher Scientific), shaking at room temperature for at least 2 h. The reaction was quenched by adding DTT to 10 mM, and the proteins were separated from excess dye by SEC in TBS (20 mM Tris pH 8.0, 100 mM NaCl).

FRET binding experiments were performed at 25 °C in TBS (20 mM Tris pH 8.0 and 100 mM NaCl) with 0.05% v/v TWEEN20 in 96-well plates (Corning 3686). Fluorescence intensity was measured using a Synergy Neo2 plate reader, exciting the donor at a 520-nm wavelength and reading acceptor emission at a 665-nm wavelength.

To measure the E2–target on-rate constant, 40 μl H2 at 10 nM was prepared in six wells. To each well, 40 μl E2–target at various concentrations was added and rapidly mixed using a multichannel pipette, and the measurement was started immediately afterwards. The following single exponential decay function was fitted to the measured FRET time courses using nonlinear least-squares minimization,

where S is the modelled fluorescence signal, S₀ is the fluorescence at equilibrium, S₁ is the amplitude of the change in fluorescence, k_app is the apparent rate constant and t is the time after the start of the measurement. The following linear function was fitted to the apparent rate constants:

where k_on and k_off are on-rate and off-rate constants and [E2] is the total concentration of E2–target.

To measure the accelerated transfer of E2 from AS114 to H2, 1,067 nM AS114 and 533 nM E2–target were incubated for 15 min to fully cage E2–target in AS114. A control solution of just 1,067 nM AS114 was also prepared. A 37.5-μl quantity of 42.7 nM H2 was prepared in eight wells; 37.5 μl of AS114 + E2–target was added to four wells and 37.5 μl of AS114 was added to the other four wells using a multichannel pipette, and the measurement was started immediately afterwards. Five minutes later, four solutions (5 μl buffer, 100 μM target, 16 μM effector or 100 μM target + 16 μM effector) were added to each set of four wells (each solution to a different well of each set) using a multichannel pipette, and the measurement was immediately continued for 1 h. Mixing components at these concentrations resulted in final concentrations of 500 nM AS114, 250 nM E2–target, 20 nM H2, 1 μM effector and 6 μM target. A baseline drift function of the following form was fitted to the AS114 + buffer data and subtracted from the other time courses:

where S is the modelled fluorescence signal, S₀ is the fluorescence at equilibrium, S₁ is the amplitude of the change in fluorescence, k is a rate constant, t is the time after the start of the measurement and t_1/2 is the time at which the fluorescence has changed by half the full amplitude. AS114 was used because, in state X, it does not clash with E2 extending past the target in E2–target.

Rapid sensors and split enzymes with luminescence readout

Luminescence experiments were performed at 25 °C in TBS (20 mM Tris pH 8.0 and 100 mM NaCl) with 0.05% v/v TWEEN20 in 96-well plates (Corning 3686). Luminescence was measured using a Synergy Neo2 plate reader with a LUM filter cube.

To measure rapid breakage of a split luciferase, 111 pM AS1–LgBiT and 22 nM target SmBiT were incubated for one hour to load AS1 with the target and reconstitute the split luciferase. Next, 72 μl of this mixture was added to two wells, then 8 μl of 1/10-diluted Nano-Glo substrate (Promega N1130) and either 10 μM effector and 200 μM target or just 200 μM target was added to these wells using a multichannel pipette, and the measurement was started immediately afterwards. Excess target was included to fully outcompete target–SmBiT to enable measurement of the dissociation rate. Mixing components at these concentrations resulted in final concentrations of 100 pM AS1–LgBiT, 20 nM target–SmBiT, 1 μM effector, 20 μM target and 1/100-diluted Nano-Glo substrate.

To measure rapid analyte sensing, 64 μl of 12.5-pM sensor was added to eight wells, 8 μl of 1/10-diluted Nano-Glo substrate was added to these wells using a multichannel pipette and the measurement was started immediately afterwards. Five minutes later, 8 μl of various concentrations of analyte obtained by tenfold serial dilution was added using a multichannel pipette, and the measurement was immediately continued for 30–60 min. Mixing components at these concentrations resulted in final concentrations of 10 pM sensor and 1/100-diluted Nano-Glo substrate. The analytes were target, effector or SARS-CoV-2 RBD (Acro Biosystems SPD-C52H3). Figure 4e shows a time course with 800 nM SARS-CoV-2 RBD.

Live-cell single-molecule imaging

For cell-surface labelling, receptors were N-terminally fused to suitable tags using a pSems vector including the signal sequence of Igκ (pSems leader). Common gamma chain (γ_c) was fused to the ALFA-tag⁸⁴ and IL-2Rβ was fused to nonfluorescent monomeric GFP (mXFP)⁸⁵. HeLa cells (ACC 57, DSMZ) were cultured as previously described⁸⁶. For transient transfection, cells were incubated for 4–6 h with a mixture of 150 mM NaCl, 10 µl of 1 mg ml⁻¹ polyethylenimine (PEI MAX, Polysciences 24765), 200 ng of DNA of pSems leader ALFA-tag-γc and 2,800 ng of pSems leader mXFPe1-IL-2Rβ⁸⁷. Labelling, washing and subsequent imaging were performed after mounting the coverslips into custom-made incubation chambers with a volume of 1 ml. Cells were equilibrated in medium with fetal bovine serum (FBS) but lacking phenol red, supplemented with an oxygen scavenger and a redox-active photoprotectant (0.5 mg ml⁻¹ glucose oxidase (Sigma-Aldrich), 0.04 mg ml⁻¹ catalase (Roche), 5% w/v glucose, 1 μM ascorbic acid and 1 μM methylviologene) to minimize photobleaching⁸⁸.

Selective cell-surface receptor labelling was achieved by using anti-GFP and anti-ALFA-tag nanobodies (NBs), which were site-specifically labelled by maleimide chemistry via a single cysteine residue at their C termini⁸⁸. Anti-ALFA NB labelled with Cy3B (degree of labelling (DOL): 1.06) and anti-GFP NB labelled with ATTO 643 (DOL: 1.0) were added at concentrations of 3 nM each, at least 10 min before imaging. Coverslips were precoated with poly-l-lysine-graft-poly(ethylene glycol) to minimize unspecific binding of NBs and were functionalized with RGD peptide for efficient cell adhesion⁸⁹.

During the imaging experiments, ASNeo2 was used at 100 nM, and 10 μM effector was used to induce receptor dissociation.

Dual-colour imaging was performed by total internal reflection fluorescence (TIRF) microscopy using an inverted microscope (IX83, Olympus) equipped with a spectral image splitter (QuadView, Photometrics) and an EMCCD camera (iXon Ultra, Andor) as described in detail elsewhere⁹⁰. Fluorophores were excited by sequential illumination with a 561-nm laser (2RU-VFL-P-2000-560-B1R, 2,000 mW, MPB Communications) and a 642-nm laser (2RU-VFL-P-2000-642-B1R, 2,000 mW, MPB Communications). Alternating laser excitation was achieved with a simple micro-controller (Arduino Uno) and open-source acquisition software⁹¹ synchronizing laser shuttering with an acousto-optic tunable filter (AOTF; AA.AOTFnC-400.650-TN, AA Opto Electronic) and camera triggering. For long-term tracking experiments, 1,500 frames per channel were acquired at 40 fps. The resulting image stacks were divided into five-frame stacks and dimerization was determined for each stack. For Fig. 5f, three time courses, each normalized to its average initial relative dimerization, are overlaid for each condition. For all other tracking experiments, 200 frames per channel were acquired at 40 fps and dimerization was determined over the whole image stack.

Dual-colour single-molecule co-tracking time-lapse images were evaluated using an in-house-developed MATLAB software (SLIMfast4C, https://zenodo.org/record/5712332)⁸⁸. After channel registration based on calibration with fiducial markers, molecules were localized using the multi-target tracking algorithm⁹². Immobile emitters were filtered out by spatio-temporal cluster analysis⁹³. Frame-by-frame co-localization within a cut-off radius of 150 nm was applied followed by tracking of co-localized emitters using the utrack algorithm⁹⁴. Molecules co-diffusing for ten frames or more were then identified as co-localized. Relative levels of co-localization were determined on the basis of the fraction of co-localized particles relative to all localizations in the ALFA-γc channel (561 nm). Diffusion properties were determined from the pooled single trajectory using mean squared displacement analysis for all trajectories with a lifetime greater than ten frames. Diffusion constants were determined from the mean squared displacement by linear regression. Relative dimerization was estimated by:

FRET efficiencies were evaluated using an in-house-developed MATLAB software (provided and described in detail elsewhere as supplementary software⁹⁰). In brief, alternating laser excitation FRET experiments provide three separated emission channels: directly excited donor \({D}_{{D}_{{\rm{ex}}}}^{{D}_{{\rm{em}}}}\) and acceptor \({A}_{{A}_{{\rm{ex}}}}^{{A}_{{\rm{em}}}}\) channels, as well as a sensitized FRET \({F}_{{D}_{{\rm{ex}}}}^{{A}_{{\rm{em}}}}\) channel. First, channels were aligned by calibration with fiducial markers. Then, after applying a single-molecule localization algorithm⁹⁵, single-molecule intensities were determined from background subtracted images (\({I}_{{D}_{{\rm{ex}}}}^{{D}_{{\rm{em}}}}\), \({I}_{{A}_{{\rm{ex}}}}^{{A}_{{\rm{em}}}}\), \({I}_{{D}_{{\rm{ex}}}}^{{A}_{{\rm{em}}}}\)). To evaluate FRET efficiencies, donor–acceptor pairs were co-localized with an optimized search radius. For these pairs, the apparent FRET efficiency was calculated by:

To achieve accurate FRET efficiencies, standard further corrections were applied. These include the donor leakage coefficient, cross-talk-corrected proximity ratio and the correction factor γ (refs. ^90,96).

pSTAT5 signalling assay with human NK (YT-1) cells

Human NK (YT-1) cells were cultured in RPMI 1640 complete medium, supplemented with 10% FBS, 2 mM l-glutamine, minimum essential non-essential amino acids, sodium pyruvate, 25 mM HEPES and penicillin–streptomycin (Gibco). For the flow-cytometry-based pSTAT5 detection assay, 2–5 × 10⁵ IL-2Rα-positive YT-1 cells were seeded in 350 µl of medium per well in a 96-well plate. The cells were stimulated with 1 nM ASNeo2 or Neo2 for 5 min at 37 °C. As a control, 50 µl of untreated YT-1 cells were set aside at the start of each experiment and evaluated after 45 min alongside the treated cells. After stimulation, all cells were transferred to three separate wells containing a control (no treatment), 10 μM effector or 40 μM ruxolitinib. One-seventh of the cells (50 µl) were resuspended in 17 µl of 16% paraformaldehyde (PFA) for immediate fixation. This process was repeated at 5-, 10-, 15-, 30- and 45-min intervals. After all of the time points were fixed, the cells were refixed in 4% PFA for 15 min at room temperature. After fixation, the cells were washed once with PBS containing 0.5% bovine serum albumin (BSA) (PBSA) and permeabilized with 100% methanol for 45 min at 4 °C. After permeabilization, the cells were washed twice with PBSA and stained for one hour at room temperature using Alexa Fluor 647-conjugated phospho-STAT5 (Tyr694) rabbit monoclonal antibody (Cell Signaling Technology, 9365, clone C71E5) diluted 1:100. After three washing steps, the cells were analysed using a CytoFlex S flow cytometer (Beckman Coulter). Data were analysed with CytExpert software, and cells were gated on SSC-A versus FSC-A. Each experiment was done in triplicate, and the results were analysed accordingly.

For Fig. 5g, pSTAT5 signal is normalized to the background level. For Fig. 5h, n = 3 time courses were normalized to the signal at time 0 (just before effector addition) and a baseline signal was determined by the average of this normalized pSTAT5 of the untreated cells, then each time course was renormalized to this baseline signal. Some batches of cells were unresponsive to stimulation; data from these batches were excluded from analysis.

Cell-line sources

HeLa cells for single-molecule imaging were sourced from the DSMZ (ACC 57); YT-1 (CD25⁺) cells were sourced from ATCC. Cell lines were authenticated by short tandem repeat profiling. HeLa cells tested negative for mycoplasma contamination by PCR.

Activation and stimulation of human T cells

Primary human peripheral blood mononuclear cells (PBMCs) isolated from a healthy donor by leukapheresis were thawed and resuspended at a cell density of 2 × 10⁶ cells per ml in T cell medium, which contained RPMI 1640 (Gibco), FBS (10% v/v, Gibco, Thermo Fisher Scientific), HEPES (25 mM, Gibco, Thermo Fisher Scientific), penicillin–streptomycin (1% v/v, Gibco, Thermo Fisher Scientific), sodium pyruvate (1% v/v, Gibco, Thermo Fisher Scientific), MEM non-essential amino acids solution (1% v/v, Gibco, Thermo Fisher Scientific) and 2-mercaptoethanol (0.1% v/v, Gibco, Thermo Fisher Scientific), and supplemented with human IL-2 (100 U ml⁻¹). For human T cell activation, cells were activated with plate-bound anti-human CD3ε (1 μg ml⁻¹, clone OKT-3, BioXCell) and soluble anti-human CD28 (5 μg ml⁻¹, clone 9.3, BioXCell) for 48 h. Cells were then expanded in T cell medium with human IL-2 (100 U ml⁻¹) for eight days. On day 9, IL-2 was withdrawn for 36 h, after which cells were resuspended at 1 × 10⁶ cells per ml and stimulated with ASNeo2 (1 nM or 5 nM) for either 5 or 25 min, as indicated. Effector peptide (10 μM) was then added to terminate signalling. After 48 or 72 h, cells were collected for counting and phenotypic analysis by flow cytometry.

For Fig. 5i,j, cells were stimulated with 1 nM ASNeo2. For Fig. 5k–n, cells were stimulated with 5 nM ASNeo2.

Flow-cytometry analyses of human T cells

For surface-marker staining, cells were collected into U-bottom 96-well plates (Thermo Fisher Scientific), blocked with Human TruStain FcX (BioLegend) and incubated with the indicated antibodies at 4 °C for 20 min, followed by live–dead staining by 4’,6-diamidino-2-phenylindole (DAPI; Thermo Fisher Scientific). Cells were then washed and resuspended with FACS buffer (PBS containing 0.2 % BSA; Sigma-Aldrich) for flow-cytometry analyses. For phospho-STAT staining, primary human T cells were rested in T cell medium lacking IL-2 for 24 h before signalling assays. Cells were plated in a 96-well round-bottom plate in 50 μl T cell medium. Cells were stimulated with 50 µl ASNeo2 for 5 min or 25 min, followed by the addition of effector peptide and incubation for another 20 min at 37 °C, and the reaction was terminated by fixation with 1.5% PFA for 15 min at room temperature with agitation. Cells were washed and permeabilized with ice-cold 100% methanol for 60 min on ice. Afterward, cells were washed with FACS buffer before staining with pSTAT5 antibodies for one hour at 4 °C in the dark. Cells were washed and resuspended in FACS buffer for flow-cytometry analyses. For caspase-3 staining, cells were first stained for surface markers and Zombie Violet Fixable Dye (BioLegend), followed by staining with a FITC Active Caspase-3 Apoptosis Kit (BD Biosciences) according to the manufacturer’s protocol. For transcription factor staining, cells were first stained for surface markers and Zombie Violet Fixable Dye, then fixed and permeabilized using a Foxp3/Transcription Factor Staining Buffer Set (eBioscience) as per the manufacturer’s instructions. Cells were subsequently incubated with the indicated antibodies for intracellular staining. Detection was performed using a CytoFlex (Beckman Coulter), and data were analysed with FlowJo (v.10.10.0).

Antibodies and reagents for flow cytometry of human T cells

The following antibodies or staining reagents were purchased from BioLegend: human CD3 (OKT3, 317324), human GATA3 (W19195B, 386906), human CD69 (FN50, 310932), human CD25 (BC96, 302611), human BCL2 (100, 658708), human Ki-67 (Ki-67, 350526), Human TruStain FcX (422302) and Zombie Violet Fixable Viability Kit (423114). The following antibodies or staining reagents were purchased from BD Biosciences: pSTAT5 (47/Stat5, 612599), and BD Pharmingen FITC Active Caspase-3 Apoptosis Kit (571606). DAPI was purchased from Thermo Fisher Scientific.

Antibodies were diluted 1:200 for surface markers (CD3, CD28, CD69 and CD25), 1:100 for intracellular proteins (GATA3, Ki-67 and BCL2) and 1:50 for pSTAT and caspase-3 staining.

Antibodies were validated by the manufacturers using flow cytometry.

qPCR

Human T cells on day 9 after activation were subjected to IL-2 starvation for 36 h. The unstimulated control cells were maintained in culture without IL-2. For transient IL-2 signalling, cells were stimulated with ASNeo2 (5 nM) for 25 min, followed by the addition of effector peptide (10 μM) to terminate signalling. For sustained signalling, ASNeo2 (5 nM) was continuously maintained in the culture medium. Total RNA was extracted using the Quick-RNA Miniprep Kit (Zymo Research) following the manufacturer’s instructions. cDNA was synthesized using the High-Capacity cDNA Reverse Transcription Kit (Thermo Fisher Scientific) with random primers. qPCR was performed using TaqMan master mix (Thermo Fisher Scientific) on a StepOnePlus Real-Time PCR System. BCL2 expression was measured using the TaqMan BCL2 assay, and gene expression was normalized to GAPDH (Thermo Fisher Scientific). Relative expression levels were calculated using the ΔΔCt method.

RNA-seq sample preparation and data analysis

Human T cells on day 8 after activation were subjected to IL-2 starvation for 36 h. The unstimulated control cells were maintained in culture without IL-2. For transient IL-2 signalling, cells were stimulated with ASNeo2 (5 nM) for 25 min, followed by the addition of effector peptide (10 μM) to terminate signalling. For sustained signalling, ASNeo2 (5 nM) was continuously maintained in the culture medium. After six hours, cells were collected, and total RNA was extracted using the Quick-RNA Miniprep Kit (Zymo Research). RNA libraries were prepared using a poly(A) enrichment-based mRNA library preparation kit following the manufacturer’s instructions. Libraries were pooled and sequenced on the NovaSeq X Plus Series (PE150). Reads were aligned to the reference genome (GRCh38) using Rsubread, and gene expression was quantified with featureCounts. For analysing pathway enrichment, gene set co-regulation analysis (GESECA) was performed with hallmark gene sets from the Human Molecular Signatures Database (MSigDB). To reduce redundancy, we performed hierarchical clustering of hallmark gene sets with Jaccard’s distance to yield eight gene-set clusters with minimal gene overlaps. Only one gene set with the lowest false discovery rate (FDR)-adjusted P value per cluster is shown in Fig. 5. Differential expression analysis was performed using DESeq2, with FDR-adjusted P < 0.05 as a threshold for differential expression. Heat maps were created using normalized counts of genes identified as differentially upregulated or downregulated in both sustained versus unstimulated and transient versus unstimulated comparisons.

Statistics and reproducibility

The main-text SPR, circular dichroism, FP, FRET and luminescence experiments, and also a subset of the DEER and SEC experiments, were performed twice (SPR in Figs. 2d,h and 4b; FRET in Fig. 4c; and SEC in Supplementary Fig. 9a) or three times (SPR in Fig. 2a,e–g; FP in Fig. 4b and Supplementary Figs. 5c and 12; luminescence in Fig. 4d,e; SEC in Supplementary Fig. 6b; and DEER with AS1 in Extended Data Fig. 2) to ensure reproducibility and low variance, and one representative experiment was reported owing to low variance among replicates. Having established low variance for these experiments, some similar measurements reported in the Supplementary Information were performed once. For all microscopy, cell staining, qPCR and RNA-seq experiments, three or four independent biological replicates were performed unless otherwise noted in the figure legend. All attempted replications of all experiments were successful, with the exception that some batches of YT-1 cells were unresponsive to stimulation; the findings in Fig. 5h were not observed with those batches. Allocation was random. No sample size calculations were performed; rather the sample sizes were chosen based on experience and were sufficient for the important observed differences between groups to be strongly statistically significant.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.