Industry-compatible silicon spin-qubit unit cells exceeding 99% fidelity

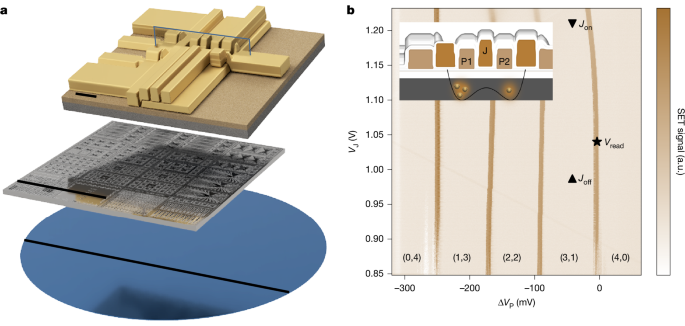
Device A exemplifies the high performance of qubits on the 300-mm wafer and can, therefore, be used as a case study to examine the sources of infidelity. In the following sections, we analyse the GST error contributions and their probable physical origins in device A, as well as its qubit performance as a function of magnetic field. Based on the consistency of the dominating errors reported in Fig. 4 and the similarity of the Larmor frequency dynamics in Extended Data Fig. 3, we expect this conclusion to hold for all four devices.

The ZI and IZ gates were implemented virtually and are, therefore, in principle error-free. However, the clock update on the field-programmable gate array took a finite time, leading to slight imperfections in these virtual operations due to idling errors. Hence, we attribute their infidelities, 0.05(4)% (0.04(4)%) for ZI (IZ), to a small time delay in the control hardware.

Most importantly, the largest contribution to infidelity for the XI, II and CZ gates is the stochastic IZ error generator, whereas the IX gate is limited by the stochastic ZI error generator, with the second highest contribution being the stochastic IZ error generator, followed by the stochastic IY error generator (Fig. 4). The stochastic dephasing error generator of the qubit undergoing a π/2 rotation (ZI for the XI gate and IZ for the IX gate) is significantly larger for the IX gate than for the XI gate. However, for the idle qubit (IZ for the XI gate and ZI for the IX gate), it is significantly larger for the XI gate than for the IX gate. Similarly, the infidelity contribution to the II gate from the stochastic dephasing error generator IZ (0.15%) is larger than for ZI (0.09%).

First, these error contributions could be explained by the coupling of ²⁹Si nuclear spins to the electron spin state of qubit 2 (ref. ⁴¹). Qubit 1 also experiences quasi-static changes in the Larmor frequency, but these are of lower magnitude, despite the Stark shifts of qubit 1 being larger (Extended Data Fig. 3). This is another indication that hyperfine-coupled residual ²⁹Si nuclear spins are the origin of that noise. As expected, these idling errors are roughly doubled (t_XI = t_IX = 400 ns) in comparison with the idling gate, which only takes around half the time. Comparing the II gate with the CZ gate, the stochastic ZI error generator remains constant (0.09%), but the IZ error generator more than doubles (0.40%), despite both gates having the same duration t_II = t_CZ = 212 ns. However, during CZ gate operation, the tunable exchange barrier is lowered to enable the Heisenberg exchange. This leads to a shift in the centre of the electron wavefunction, possibly moving qubit 2 closer to the ²⁹Si nuclear spin, thus increasing the contact hyperfine interaction and the quasi-static noise in IZ.

Second, it might seem contradictory that the gate infidelity is dominated by noise in qubit 2, given that \({T}_{2,{\rm{Q}}2}^{{\rm{Hahn}}} > {T}_{2,{\rm{Q}}1}^{{\rm{Hahn}}}\) and \({T}_{2,{\rm{Q}}2}^{* }\approx {T}_{2,{\rm{Q}}1}^{* }\). However, the GST experiments are designed to amplify, not echo out, persistent noise sources. They are, therefore, heavily affected by slow noise, such as Larmor frequency changes arising from hyperfine-coupled nuclear spins. On the other hand, Hahn echo experiments are limited by fast charge noise. The Larmor frequency variation, tracked during the GST experiment using real-time feedback^39,40, shows a higher standard deviation for the qubit 2 frequency variation compared with qubit 1 (Extended Data Fig. 3). Furthermore, the infidelities of the XI, IX, II and CZ gates decrease for higher Larmor feedback rates, with the main contribution again being the stochastic IZ error generator for the XI, II and CZ and the stochastic ZI error generators for the IX gate (Extended Data Fig. 6).

Third, sequences between which the Larmor frequency feedback exhibits a large frequency change can be removed from the GST dataset, but this has a significant effect only on the stochastic IZ error generator of the XI gate (Extended Data Fig. 7). Moreover, the spread of the Larmor frequency is independent of B₀, whereas the Stark shift increases linearly (Extended Data Figs. 8 and 9) and the spin–orbit interaction in qubit 1 is stronger compared with qubit 2, as can be seen in Fig. 3a,b. The standard deviation of the Larmor frequency feedback increases in a step-like manner as a function of total experiment runtime for distinct instances across all magnetic fields (Extended Data Fig. 10). Hence, these slow timescale jumps probably originate from qubit 2 coupling strongly to the nuclear spin states of the residual ²⁹Si atoms. As such, they contribute significantly to the gate infidelities and are the cause of the above-described observations^2,42,43. These slow jumps in the Larmor frequency do not contribute to \({T}_{2}^{{\rm{Hahn}}}\) and, therefore, do not contradict \({T}_{2,{\rm{Q}}2}^{{\rm{Hahn}}} > {T}_{2,{\rm{Q}}1}^{{\rm{Hahn}}}\).

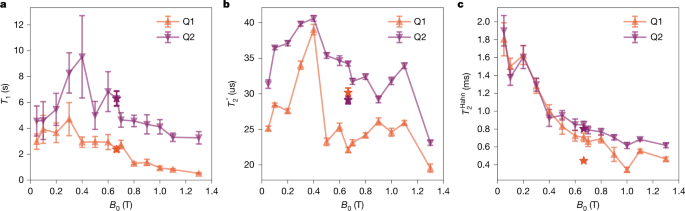
In terms of qubit device performance, Fig. 5 shows spin lifetime and coherence metrics as functions of the magnetic field B₀. T₁ and \({T}_{2}^{* }\) first increase up to B₀ = 0.3–0.4 T, followed by a decrease for larger B₀. Because \({T}_{2}^{* }\) is sensitive to d.c. noise, it samples 1/f noise down to frequencies corresponding to the total time of the experiment, which renders it a bad metric for comparing different qubits or qubit platforms. Including Larmor frequency feedback in the experiment reduces the contribution of low-frequency 1/f noise⁴⁴. We demonstrate this in Extended Data Fig. 11a,b by plotting \({T}_{2}^{* }\) as a function of the cumulative measurement time. Most curves are approximately flat, showing the effectiveness of the feedback mechanism. Extended Data Fig. 11c,d show the variation of \({T}_{2}^{* }\) as a function of laboratory time.

a–c, Spin lifetime T₁ (a), Ramsey \({T}_{2}^{* }\) (b) and Hahn echo \({T}_{2}^{{\rm{Hahn}}}\) (c) metrics as functions of the applied magnetic field amplitude B₀. We measured both qubits for each experiment interleaved and repeated this 50 (T₁), 10,000 (\({T}_{2}^{* }\)) and 2,000 (\({T}_{2}^{{\rm{Hahn}}}\)) times. Ramsey experiments at B₀ = 0.05 T, 0.1 T, 0.8 T and 1.1 T were repeated 50,000, 100,000, 50,000 and 40,000 times. The Hahn echo experiment at B₀ = 1.3 T was repeated 500 times. Between each repeat we used real-time Larmor frequency feedback following the protocol described in ref. ³⁹. The data were fitted using the functions described in Extended Data Fig. 2. Data shown as stars correspond to metrics measured during two-qubit benchmarking (Extended Data Fig. 2), using a method and gate voltages that differed from those used for the magnetic field sweep. Error bars represent the 95% confidence level.

The longest measured coherence times for device A include Hahn echo coherence time \({T}_{2}^{{\rm{Hahn}}}=\text{1,900}\,{\rm{\mu }}{\rm{s}}\) (1,805 μs) for qubit 2 (qubit 1) measured at the low magnetic field of B₀ = 50 mT, as well as \({T}_{2}^{* }\) = 40.6 μs (39.0 μs) and T₁ = 9.5 s (4.7 s). The long \({T}_{2}^{{\rm{Hahn}}}\) and its small variation between both qubits indicate that magnetic noise dominates at low fields. On increasing B₀, the Stark shift increases linearly (Extended Data Fig. 9), with steeper slopes for qubit 1 (ΔΩ_Stark(P1, J, P2) = (−19.9(4), 31.3(3), 14.2(4)) MHz V⁻¹ T⁻¹) than for qubit 2 ((0, 3.2(2), 16.7(4)) MHz V⁻¹ T⁻¹), manifesting in stronger coupling to charge noise through the spin–orbit interaction and resulting in reduced coherence, with a 33% larger \({T}_{2,Q2}^{{\rm{Hahn}}}=617(26)\,{\rm{\mu }}{\rm{s}}\) (\({T}_{2,Q1}^{{\rm{Hahn}}}=464(22)\,{\rm{\mu }}{\rm{s}}\)) at B₀ = 1.3 T. The observed Stark shift is entirely caused by the intrinsic spin–orbit coupling of silicon electrons confined at the Si/SiO₂ interface. For device A, the external magnetic field points in the [110] lattice orientation, where the variability of the g factor is highest and the Dresselhaus spin–orbit component dominates. This type of spin–orbit coupling is largely influenced by atomistic roughness at the Si/SiO₂ interface²⁹. In the presence of a gate bias, the quantum dot moves under the rough interface, shifting its g factor. The magnitude and sign of the resulting Stark shift depends on the direction in which the gate moves the quantum dot. Typical values range between −80 MHz V⁻¹ T⁻¹ to 80 MHz V⁻¹ T⁻¹ (ref. ²⁵). In device A, we obtained −20 MHz V⁻¹ T⁻¹ to 30 MHz V⁻¹ T⁻¹, which falls within that range. The magnetic field dynamics of the spin coherence times are distinct from previous results for academic devices⁷, and the exact physical origin requires a more detailed study, which is beyond the scope of this work.

Looking forward, the increase in \({T}_{2}^{{\rm{Hahn}}}\) for low fields is extremely encouraging because it indicates that the qubits are amenable to more scalable control techniques. Such approaches continuously drive the spin by using a modulated microwave field to decouple it from noise and eliminate free precession (\({T}_{2}^{{\rm{Hahn}}}\gg {T}_{2}^{* }\))^36,45. Operation at lower fields requires a different modality of the two-qubit gate. To achieve similarly fast gates, a SWAP-like operation will be implemented. Furthermore, at low fields an always-on, global control is beneficial for avoiding idling errors and using the long decoupling times \({T}_{2}^{{\rm{Hahn}}}\gg {T}_{2}^{* }\) observed. This can be achieved by aligning the magnetic field direction such that the Larmor frequencies of the qubits become degenerate⁴⁵. The key challenge for that operation modality is sufficiently large Stark shifts.

Our chosen implementation of an entangling gate (CZ) is faster than decoupling schemes, but it relies on the exchange interaction being smaller than the Zeeman energy difference of the two qubits (J_exc ≪ ΔE_Z). We chose B₀ values in the range 0.662–0.7 T to meet this requirement, but in future, we intend to explore other two-qubit gate implementations⁸.