Stratified wind from a super-Eddington X-ray binary is slower than expected

Data extraction

XRISM

Data reduction was performed with the software versions of the pre-pipeline version JAXA ‘004_002.15Oct2023_Build7.011’ and the pipeline script ‘03.00.011.008’, and the internal CALDB8, which corresponds to the public XRISM CALDB v.20240815.

The Resolve data were filtered to exclude periods affected by the eclipse of Earth, the sunlit limb of Earth, South Atlantic Anomaly passages, and the initial 4,300 s following the recycling of the 50-mK cooler. Events in the resulting good time intervals were screened using pixel-to-pixel coincidence and an energy-dependent rise time cut^54,55. Pixels 12 (calibration pixel) and 27 (which shows unexpected gain fluctuations) were excluded. The net exposure time after filtering was 37.8 ks, with a total count rate of 72.1 s⁻¹.

A timing coefficient in the CALDB is used to set a flag for any event occurring near-in-time to another event on another pixel. The false coincidence for pixel–pixel coincidence may not be ignored, especially in the bright sources, but in our observations, the loss fraction calculated from the STATUS[4] flag is only about 10%.

Calorimeter events are classified into grades based on the time interval from temporally adjacent events. Here, we use only high-resolution primary (Hp) grade, which provides the highest energy resolution. The Hp count rate was 30.1 s⁻¹, representing 42% of the total. A redistribution matrix file was generated using rslmkrmf based on the cleaned event file, with a parameter file of xa_rsl_rmfparam_20190101v006.fits. The line-spread function components considered included the Gaussian core, exponential tail to low energy, escape peaks, silicon fluorescence and electron loss continuum (that is, the ‘X’ option was selected). An auxiliary response file was generated using xaarfgen, assuming a point-like source at the aim point, including the additional opacity of the gate valve closed current configuration of Resolve⁵⁶.

The temperature sensitivity of the Resolve detector necessitates pixel-by-pixel correction for gain drift to maintain proper energy scale and resolution. The gain scale function is parameterized by an ‘effective temperature’⁵⁷, which was tracked over time for each pixel. The Mn Kα line complex from the ⁵⁵Fe calibration source was used to calculate the effective temperature. Two gain fiducial measurements were performed at the start and end of the observation, in which the entire array was illuminated by the ⁵⁵Fe source in the filter wheel. The Mn Kα spectrum, shown in Extended Data Fig. 1, has an energy resolution of 4.43 ± 0.16 eV (full-width at half maximum) and an energy offset of less than 0.16 eV. A significant temperature shift was identified after the observation, attributed to spacecraft manoeuvres and orientation. In the calibration pixel, continuously illuminated by ⁵⁵Fe, the effective temperature shifted from 49.969 mK to 49.965 mK and then to 49.975 mK (Extended Data Fig. 2). If the gain drift were tracked only at the fiducial points, the maximum effective temperature shift would be 0.005 mK, corresponding to a 1.5-eV energy shift (Extended Data Fig. 2). To reduce this shift, we introduced an ad hoc gain point (Extended Data Fig. 2, red circle) and calculated the effective temperature difference (ΔT_eff) between the initial and ad hoc gain point. Scaling from the gain change on the calibration pixel at this intermediate point, we added a new gain point for each of the other pixels (Extended Data Fig. 3) and corrected the X-ray energies using linear interpolation. After this observation, a gain fiducial 9 h after a manoeuvre was added to standard operations.

At high count rates, energy resolution degradation may occur because of contamination from untriggered electrical cross-talk events⁵⁸. To evaluate this effect, we use spectra of Cr Lyα₁ and α₂ lines from the source, which are strong and close in energy to the Mn Kα calibration lines. We compare these before and after cross-talk effect screening, but the line widths do not change significantly. The results indicate that cross-talk has a negligible effect on the energy resolution in this observation. Therefore, we do not apply cross-talk screening to preserve photon statistics.

We also check whether there is contamination of the data from pseudo-Ls (low-resolution secondary) events. However, this is more important for fainter sources and is negligible below 10 keV.

The data are not corrected for any systemic velocity offsets, because these are small, with a blueshift of 40 km s⁻¹ for the combined effects of the velocity of the Earth around the Sun and the galactic rotation at GX 13+1 position with respect to the local standard of rest. The peculiar velocity of the binary system is also fairly small, at −70 ± 30 km s⁻¹ (ref. ¹⁰).

NuSTAR

We use the nupipeline from HEASOFT v.6.33.2 to reduce NuSTAR observation 30901010002. We use nuproducts to extract NuSTAR source and background spectra and to create response files. The source region is a 1 arcmin circle centred on the source; we used surrounding source-free regions for background.

The NuSTAR observation took place from 25 February 2024 12:56:09 UT to 26 February 2024 10:36:00 UT, and the XRISM observation occurred between 25 February 2024 02:26:51 UT and 26 February 2024 00:06:46. Therefore, to maximize simultaneity and mitigate the effects of any source variability, we define the NuSTAR good time interval as the beginning of the NuSTAR observation to the end of the XRISM observation.

Ion-by-ion model fitting

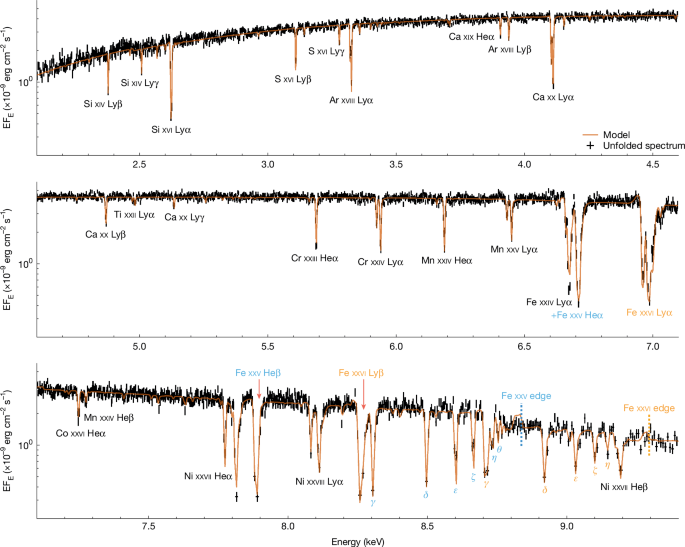
Disk-accreting neutron star continuum spectra are generally well modelled by a multicolour disk component, together with higher temperature emission from a boundary layer between the disk and the neutron star surface. The boundary layer illuminates the disk, producing a characteristic reflection spectrum that is broadened by the relativistic velocities and strong gravity of the inner disk. We approximate this component with a broad Gaussian emission line with energy fixed at 6.4 keV. The XRISM spectra are rebinned to require 20 counts per bin and fit between 2.1 keV and 18 keV using the xspec⁵⁹ X-ray spectral fitting package.

Relative to this absorbed disk plus blackbody and Gaussian continuum, the fit residuals show numerous narrow absorption features. We first model these features by considering each ion independently. The kabs model²⁸ (a local model for use in xspec software) calculates the full Voigt absorption line profile for a single transition in a given ion. Modelling the full series of transitions from n = 1 for a given ion then involves multiple KABS components, with the ion column and velocity outflow and width tied across all the components. We develop a more convenient xspec local model, Ionabs, which packages all these together, calculating the full line series from a given ion column with given kinematics in a single model component. This includes all fine structure lines, as well as the self-consistent edge structure(s) (including the L-shell edge for ions with three or more electrons, such as Fe xxiv). The Voigt profile velocity width in KABS is defined as v_turb/c = (E − E₀)/ΔE, but the photoionization code pion (see below) uses the Gaussian width \({v}_{{\rm{rms}}}/c=(E-{E}_{0})/(\,\sqrt{2}\Delta E)\), so here we report v_rms so that these can be directly compared. Transition energies, oscillator strengths, Einstein A values and the energy dependence of the cross-sections are taken from Flexible Atomic Code⁶⁰. These match very well with the NIST database for H- and He-like ions.

Most of the lines have a similar kinematic structure with slow outflow velocity and a very narrow velocity width. This ‘slow’ wind component must have a very high column density to produce the multiple higher-order lines (transitions beyond n = 8) of Fe xxv and Fe xxvi. This column should have corresponding n = 2–1 Kα transitions, which are completely saturated, so that the line cores are completely black. The fact that the data never go to zero shows that there is an additional diffuse source of X-rays, most likely from the wind itself (Fig. 3). Moreover, the detailed Fe xxvi Kα₁,₂ line profile shows a strong blue wing, requiring that there is an additional, faster wind component present (Fig. 3).

Thus, we model the intrinsic spectrum absorbed by two wind components: slow (16 ions) and fast (only Fe xxv, Fe xxvi, Ni xxvii and Ni xxviii). Modelling the diffuse emission is more challenging, as it should be extremely complex, with recombination radiation from the X-ray heated material and scattered incident continuum forming a spatially extended source that is absorbed along multiple different lines of sight through the wind. We first approximate this as electron scattering alone, so a fraction f_scatt of the incident continuum, but a better fit to the remaining residuals around the absorption lines is if the scattered continuum is also absorbed by the fast wind component.

The model then consists of the intrinsic continuum Int=(diskbb+gauss+bbody), absorbed by multiple ions grouped into two kinematic components (slow: Ionabs_s and fast: Ionabs_f), together with photoelectric absorption from neutral material (TBabs) fixed at the interstellar column density of N_H = 3.2 × 10²² cm⁻². The model is \({\rm{TBabs}}\times ({{\rm{Ionabs}}}_{{\rm{s}}}^{{\rm{16}}}\,{{\rm{Ionabs}}}_{{\rm{f}}}^{{\rm{4}}}+{{\rm{f}}}_{{\rm{scatt}}}\,{{\rm{Ionabs}}}_{{\rm{f}}}^{{\rm{4}}})\times {\rm{Int}}\) in XSPEC notation, in which the superscripts on Ionabs show the number of ions included.

The resulting fit parameters are given in Extended Data Table 1. The ions in the slow component all have similar outflow velocities of v_out ~ 330 km s⁻¹. The fast component seems to have a wider range of kinematics, with outflow velocities ranging from about 500–1,000 km s⁻¹ depending on the ion, but both fast and slow components have line widths of around v_out/2.

The column densities derived for the ions in the slow component (Extended Data Table 1) are almost an order of magnitude larger than found in previous Chandra or HETGS data (ref. ¹⁵). We estimate a lower limit to the equivalent hydrogen column density from adding the slow component Fe xxv and Fe xxvi ion columns together, to get \({N}_{{\rm{Fe}}}=4{6}_{-5}^{+6}\times 1{0}^{18}\,{{\rm{cm}}}^{-2}\), giving N_H > N_Fe/A_Fe = 1.4 ± 0.2 × 10²⁴ cm⁻² for A_Fe = 3.3 × 10⁻⁵.

This column density is large enough that electron scattering optical depth is significant: τ_es = 1.21N_Hσ_T ≳ 1.1, where the factor 1.21 comes from the number of electrons per hydrogen atom in a fully ionized plasma of solar abundance and σ_T is the Thomson cross-section. The observed Fe ion columns in the slow wind component already imply that the wind is optically thick to electron scattering, and yet there should be even more material, first because of the fast wind and second because some fraction of Fe is completely stripped to Fe xxvii, and hence produces no line signatures. This correction need not be very large for the slow wind, for which the ratio of columns Fe xxvi/Fe xxv is close to unity. However, this is not true for the fast wind, for which the column in Fe xxvi is 2.5 times larger than that of Fe xxv. Thus, the observed ion columns in the fast wind are probably only a small tracer of the likely column present. To correct for this, an ionization balance calculation needs to be done.

Photoionization modelling for ion fractions

We use the photoionized plasma model pion v.3.08.00, available in SPEX (refs. ^23,61). We compute the ratios of different ionization stages Nⁱ⁺¹/Nⁱ (Extended Data Fig. 4) and the ion fractions (Extended Data Fig. 5) as functions of the ionization parameter log ξ ≡ L/(nR²). We assume an intrinsic illuminating continuum that matches the best-fit incident continuum (disk blackbody plus blackbody).

All the ion ratios in the slow component are consistent with those from Fe xxvi/Fe xxv alone, giving an ionization parameter of log ξ = 3.85–3.98. This gives an ion fraction for completely ionized iron (Fe xxvii) of f_xxvii = 0.14–0.23 (Extended Data Fig. 5). This increases the total iron column density in the slow wind to N_Fe = 51–60 × 10¹⁸ cm⁻², leading to an equivalent hydrogen column density N_H = N_Fe/A_Fe = 1.5–1.8 × 10²⁴ cm⁻² and τ_es = 1.2–1.4.

A similar analysis for the fast wind gives a more complex picture. The Fe ratio suggests log ξ  = 4.15–4.29 (corresponding to ion fraction of Fe xxvii 0.38–0.53), giving N_H ~ 4.3–5.6 × 10²² cm⁻². However, these broader lines are less well-defined in the data, and therefore more sensitive to the model assumed to approximate the complex diffuse emission from the wind. Thus, the column density of the faster component is much more uncertain (see the full photoionization fits below).

The unabsorbed continuum model (without scattered flux) gives a bolometric flux of F = 9.1 × 10⁻⁹ erg cm⁻² s⁻¹ (13.6–100 keV). Correcting this for attenuation by electron scattering with τ_es = 1.2–1.4 gives an intrinsic flux of F₀ = 3.0–3.8 × 10⁻⁸ erg cm⁻² s⁻¹. The luminosity of this source L = 4πd²F₀ = 0.8 − 1L_Edd, where d = 7 kpc and L_Edd = 2.1 × 10³⁸ erg s⁻¹.

The scattered fraction parameter in these fits f_scatt is the ratio of scattered to observed direct flux. We use this to calculate the ratio of scattered to intrinsic flux F_scatt/F₀ = 0.052–0.066 and use this to estimate the solid angle of the wind, as F_scatt/F₀ ≈ Ω/4π(1 − exp(−τ_es)). This gives Ω/4π = 0.08 ± 0.01, although again this is quite uncertain as it depends on the detailed wind geometry and emission or absorption.

Fitting with photoionization models

We now use the same photoionized code, PION, to directly fit to the data. We calculate a grid of models for solar abundances, simulating absorbers with different values of column density N_H, ionization parameter log ξ and turbulent velocity v_rms, fixing the illuminating SED shape to that derived from spectral fitting. Each of the simulations has 65,536 logarithmically spaced bins to cover the energy range from 10⁻⁴ keV to 10³ keV with a resolution of 1.5 eV around 6 keV, enough to fit Resolve data. In total, we perform 8,736 simulations with values 21 ≤ log N_H ≤ 25 spaced by 0.2 (21 points), 2 ≤ log ξ ≤ 7 spaced by 0.2 (26 points), and −5 ≤ log(v_rms/c) ≤ −2 spaced by 0.2 (16 grid points). We fit with a single number density n_p = 10¹⁴ cm⁻³ to reduce the size of the tables (see the main text and below). We calculate the population levels from radiative recombination, cascade, radiative and collisional excitation correctly for meta-stable levels^42,62. We build these results into a multiplicative absorption table model⁴⁶ for use in XSPEC.

Diffuse continuum approximated by absorbed scattered flux

We replace the multiple ion-by-ion absorption components with two pion absorption components (one fast: abs_f and the other slow: abs_s). As above, we assume that the diffuse emission has the same shape as the incident continuum and that this scattered component is absorbed by the fast wind. We represent this model in XSPEC form as TBabs × (abs_sabs_fInt + f_scattabs_fInt).

The goodness of the fit is not far from that of the ion-by-ion fit, which allowed free element abundances and allowed every ion to have different kinematics and ion ratios (χ² = 14,726/13,555, that is, 52 fewer free parameters, for Δχ² ~ 550). This gives very similar plasma parameters for the slow component as derived from the ion-by-ion fitting, namely, \(\log \,\xi =3.9{3}_{-0.02}^{+0.01}\) and \({N}_{{\rm{H}}}=15{4}_{-6}^{+8}\times 1{0}^{22}\,{{\rm{cm}}}^{-2}\). However, the fast component now has a higher ionization parameter (log ξ = 4.49) and hence a higher equivalent column density of \({N}_{{\rm{H}}}={9}_{-1}^{+2}\times 1{0}^{22}\,{{\rm{cm}}}^{-2}\). This shows that the fast component parameters are more sensitive to the details of the model, but that the slow component is very robust, and robustly gives an optical depth τ_es > 1.

Diffuse component, including line and recombination emission

A better approximation to the diffuse and scattered continuum requires using pion to calculate the emitted line and recombination continua from the photoionized material, apart from the absorption lines. We take the same incident spectrum and density as for the absorption table model to generate an additive table model for XSPEC (hereafter emm), but this time we set the solid angle fraction Ω/4π = 1.0. In principle, the resulting emission normalizations allow the solid angle to be independently estimated, but these are dependent on the details of the radiation transfer through the optically thick wind, so we do not use them here.

We tie the ionization parameter and column density to be the same for the absorbing and emitting plasma. We expect that the emission should arise from all azimuths, so we fix the outflow velocity to zero and allow the broadening to be free. We allow this to be self-absorbed by the wind in our line of sight, but caution that this is just an approximation to a more complex geometry that requires a full radiation transfer calculation.

The final model is TBabs × (abs_sabs_fInt + f_scattabs_fInt + abs_semm_f + f_scattemm_f + emm_s), where again we fix TBabs to the interstellar column density of N_H = 3.2 × 10²² cm⁻². This gives our best description of the spectrum (Extended Data Table 2), and is the model shown in Fig. 1. This gives a goodness of fit of 14,339/13,551. This has four more free parameters than the previous description of the diffuse flux, but gives Δχ² = −386. It is now statistically equivalent to the ion-by-ion fits in Extended Data Table 1, because it has 48 fewer free parameters for an increase of Δχ² = +151.

It is difficult to see the emission lines in this model because they are dominated by the fast component and are therefore moderately broadened. Nonetheless, the resultant P Cygni profile can be seen in Fe xxvi Lyα_1,2 at around 6.94 keV as shown in Fig. 3. The emission lines also contribute to the shape of the saturated line cores, and this more complex model shifts the ionization parameter of the fast wind to even higher values, \(\log \,\xi =4.6{9}_{-0.04}^{+0.03}\) requiring even higher column densities: N_H = 80 × 10²² cm⁻². Again, the parameters of the slow wind are mostly consistent with previous models, with just slightly lower column (\({N}_{{\rm{H}}}=13{2}_{-8}^{+7}\times 1{0}^{22}\) cm⁻²) and ionization state (log ξ = 3.88 ± 0.01), but similar kinematics and scattered fraction.

We also perform fits with the XSTAR model warmabs⁶³ to explore the overall robustness of our photoionization analysis. For warmabs, we calculate electron-level populations using the best-fit continuum from fits to a model consisting of an absorbed disk plus nthcomp^64,65 with Gaussian lines and a smeared edge near 8 keV. Fits to the Resolve spectrum with warmabs were qualitatively and quantitatively very similar to the pion fits, requiring a high-column component with a smaller turbulent line width and blueshift and a more highly ionized, broader and faster component. These fits will be presented in detail elsewhere, but we note that despite different assumptions about the ionizing continuum, radiative transfer, absorption and emission geometry, and the different codes, we still find a total equivalent of the slow wind column density in excess of 1.4 × 10²⁴ cm⁻².

Wind geometry

We assume that the wind is a continuous structure so the outer edge of the fast wind must coincide with the inner edge of the slow wind³². In other words, the column density of the fast and slow winds must be given by

where R_s = R_f + ΔR_f, ΔR_f is the width of the fast wind and n(R) is the density profile of the wind. But the relative locations of the fast and slow winds are also set by their relative ionization parameters. If the ionization parameter at the inner edge of the fast wind is \({\xi }_{{\rm{f}}}={L}_{0}/{n}_{{\rm{f}}}{R}_{{\rm{f}}}^{2}\), then the ionization parameter at the inner edge of the slow wind must be \({\xi }_{{\rm{s}}}={L}_{0}\exp (-{\tau }_{{\rm{f}}})/{n}_{{\rm{s}}}{R}_{{\rm{s}}}^{2}\). Here n_f and n_s are the densities of the wind at R_f and R_s, respectively, whereas R_out is the outermost radius at which the wind is produced (which need not be the same as the disk outer radius). The factor exp(−τ_f) is an approximation of the attenuation of the radiation field by the fast wind. This is appropriate for a relatively small solid-angle wind, as inferred here.

For a self-consistent solution, the radius of the slow wind as inferred from the column density of the fast wind must match the radius implied by the relative ionization of the two zones. This gives four independent constraints, so we can solve for (at most) four independent parameters. We first assume a constant density wind, which gives n_f = n_s = 1.6 × 10¹⁴ cm⁻³, for R_f = 4.7 × 10⁹ cm, R_s = 1.0 × 10¹⁰ cm and R_out = 1.8 × 10¹⁰ cm. Alternatively, we assume a power law density distribution \(n={n}_{{\rm{f}}}{(R/{R}_{{\rm{f}}})}^{-x}\) for R_f < R < R_out = 10¹² cm, which is the outer disk radius. This has n_f = 0.9 × 10¹⁴ cm⁻³ with x = 1.1 for R_f = 6.3 × 10⁹ cm, R_s = 3.7 × 10¹⁰ cm (giving n_s = n(R_s) = 1.3 × 10¹³ cm⁻³).

These densities are very high, but the predominantly H- and He-like ions seen have no density diagnostic potential. Instead, previous work on the black hole binary GRO J1655-40, which also showed evidence for a Compton-thick wind from a likely super-Eddington state^30,42,66,67, measured density directly from a meta-stable L-shell absorption line of B-like Fe xxii (refs. ^42,68,69). This line transition at about 1 keV is outside of the current Resolve bandpass, and would probably not be present in the higher ionization state seen in the GX 13+1 outflow. However, weak meta-stable lines from K-shell Be-like Fe xxiii around 6.6 keV may be used to probe the density⁶² in future modelling.

In principle, a thermal wind may be launched from all radii R ≳ 0.2R_IC, where R_IC is the Compton radius³⁷. For GX 13+1, this nominal limit is approximately 3.3 × 10¹⁰ cm, a factor of a few larger than the inferred launch radius of the fast wind. However, thermal-radiative winds can be expected from much smaller radii when the luminosity approaches the Eddington limit³⁵, so our radii are probably consistent with a thermal-radiative wind.

Finally, we calculate the mass loss rate in the wind. Here the wind is being launched from all radii on the disk from R_f − R_out, so we cannot use the standard mass continuity expressions as the wind mass is increasing over this range. Instead, we calculate the total wind mass in this region, M, and the time, t, it takes to expand out of this region as

where m = 2.4 × 10⁻²⁴ g is the average atomic mass per hydrogen atom in a cosmic gas, Ω is the solid angle of the wind and v(R) is the radial velocity profile.

For the constant density wind, these give \(\dot{M}=M/t=2.4-6.6\,\times \) \(1{0}^{18}\,{\rm{g}}\,{{\rm{s}}}^{-1}\) for the solid angles discussed in the main text (0.08 ≤ Ω/4π ≤ 0.22). This is very similar to the estimates given by mass continuity \(\dot{M}=4{\rm{\pi }}{R}^{2}n(R)v(R)m(\varOmega /4{\rm{\pi }})\), which can be rewritten for the fast wind as \({\dot{M}}_{{\rm{f}}}=4{\rm{\pi }}m(\varOmega /4{\rm{\pi }})(L/{\xi }_{{\rm{f}}})=0.5-1.5\times 1{0}^{18}\,{\rm{g}}\,{{\rm{s}}}^{-1}\), whereas the slow wind gives \({\dot{M}}_{{\rm{f}}}=4{\rm{\pi }}m(\varOmega /4{\rm{\pi }})L\exp (-{\tau }_{{\rm{f}}})/{\xi }_{{\rm{s}}}=1.3-3.7\times 1{0}^{18}\,{\rm{g}}\,{{\rm{s}}}^{-1}\). However, the power law density profile with x = 1.1 has much more mass at larger radii, so it gives much larger \(\dot{M}=M/t=14-39\times 1{0}^{18}\,{\rm{g}}\,{{\rm{s}}}^{-1}\).

Even the lowest estimates for the mass loss rate from constant density assumptions are comparable with the central mass accretion rate of 3.9 × 10¹⁸ g s⁻¹ required to power the inferred X-ray luminosity, whereas the largest estimates have up to 10 times more matter ejected than is accreted.