Learning the natural history of human disease with generative transformers

Data

UK Biobank

Cohort

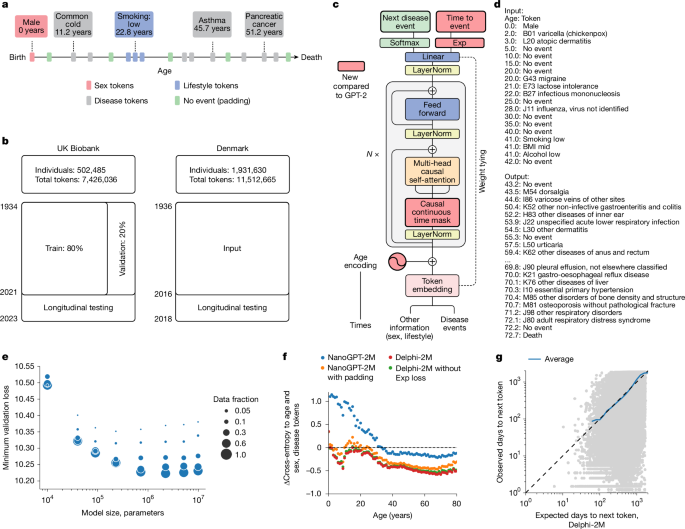
The UK Biobank is a cohort-based prospective study comprising approximately 500,000 individuals from various demographic backgrounds recruited across the UK between 2006 and 2010. At the time of recruitment, individuals were between 37 and 73 years of age³⁵.

Disease first occurrence data

The main data source for health-related outcomes is built on the first occurrence data assembled in category 1712 from the UK Biobank. These data include ICD-10 level 3 codes (for example, E11: type 2 diabetes mellitus) for diseases in chapters I–XVII, excluding chapter II (neoplasms), plus death. The data are pre-assembled by UK Biobank and include the first reported occurrence of a disease in the linked primary care data (cat. 3000), inpatient hospital admissions (cat. 2000), death registry (fields 40001 and 40002) or self-reported data through questionnaires (field 20002).

Information on neoplasms was not included in category 1712 by the UK Biobank, and we therefore included the data ourselves through the addition of the linked cancer registry data in fields 40005 and 40006 (subset to the first occurrence and mapped to ICD-10 level 3 codes), which, combined with first occurrence data, gives in total 1,256 distinct diagnoses. A list of all codes used is provided in Supplementary Table 5.

Lifestyle and demographics

We extract information on the self-reported sex of participants as recorded in field 31 (indicators for female and male), a physical assessment of body mass index at recruitment from field 21001, which we split into three indicators encoding BMI < 22 kg m⁻², BMI > 28 kg m⁻² and otherwise, as well as smoking behaviour from field 1239 with indicators for smoker (UKB coding: 1), occasionally smoking (2) and never smoker (0) and alcohol intake frequency from field 1558 with indicators for daily (1), moderately (2, 3) and limited (4, 5, 6).

Furthermore, information that we extracted and used for stratification to assess model performance in subgroups but were not part of the data for model training include self-reported ethnic background (field 21000), with participants grouped into five level groups (white, mixed, Asian or Asian British, Black or Black British, and Chinese) and an index of multiple deprivation as available in field 26410. The index combines information across seven domains, including income, employment derivation, health and disability, education skills and training, barriers to housing and services, living environment and crime.

Moreover, we extract information required for some of the algorithms we compare against. A list of the variables and their codes can be found in Supplementary Table 5.

Danish registries

Cohort

Exploring comorbidities and health-related factors is uniquely facilitated by Denmark’s comprehensive registries, which gather up to 40 years of interconnected data from across the entire population. All used registries are linkable through a unique personal identification number provided in the Central Person Registry along with information on sex and date of birth. Furthermore, we used the Danish National Patient Registry³⁶ (LPR), a nationwide longitudinal register with data on hospital admissions across all of Denmark since 1977, along with the Danish Register of Causes of Death³⁷ since 1970 to extract information on an individual’s acquired diagnoses throughout their lifetime. Our current data extract covers information up until around 2019 when reporting to the LPR was updated to LPR3. Furthermore, we restrict our cohort to individuals 50–80 years of age on 1 January 2016, to obtain a similar age range as in the UK Biobank. The 1 January 2016 was chosen as the cut-off point as it is the latest timepoint for which we can guarantee reliable coverage across the entire population over the entire prediction horizon.

Feature adjustments

To obtain a dataset that resembles the UK Biobank data, we retain only the first occurrence of an individual’s diagnosis and transform all codes to ICD-10 level 3 codes. Diagnoses before 1995 are reported in ICD-8 and have been converted to ICD-10 codes using published mappings³⁸. Codes that may be present in the Danish register but were not in the UK Biobank are removed. Information on lifestyle is not available, and indicators for BMI, smoking and alcohol intake have therefore been treated as absent.

Data splits

UK Biobank

The models were trained on UK Biobank data for 402,799 (80%) individuals using data from birth until 30 June 2020. For validation, data contain the remaining 100,639 (20%) individuals for the same period. Internal longitudinal testing was carried out using data for all individuals still alive by the cut-off date (471,057) and evaluated on incidence from 1 July 2021 to 1 July 2022, therefore enforcing a 1 year data gap between predictions and evaluation. Validation assesses how well the model generalized to different individuals from the same cohort. Longitudinal testing investigates whether the model’s performance changes over time and if it can be used for prognostic purposes.

Denmark

External longitudinal testing was conducted on the Danish registries. All individuals residing in Denmark 50–80 years of age on the 1 January 2016 were included. Predictions are based on the available data up to this point and were subsequently evaluated on incidence from 1 January 2017 to 1 of January 2018, similar to the internal longitudinal testing. Data were collected for 1.93 million individuals (51% female and 49% male), with 11.51 million disease tokens recorded between 1978 and 2016. Predictions were evaluated on 0.96 million disease tokens across 796 ICD-10 codes (each with at least 25 cases).

Model architecture

GPT model

Delphi’s architecture is based on GPT-2 (ref. ⁶), as implemented in https://github.com/karpathy/nanoGPT. The basic GPT model uses standard transformer blocks with causal self-attention. A standard lookup table embedding layer with positional encoding was used to obtain the embeddings. The embedding and casual self-attention layers are followed by layer normalization and a fully connected feedforward network. Transformer layers, consisting of causal self-attention and feedforward blocks, are repeated multiple times before the final linear projection that yields the logits of the token predictions. The residual connections within a transformer layer are identical to those in the original GPT implementation. Here we also use weight tying of the token embeddings and final layer weights, which has the advantage of reducing the number of parameters and allowing input and output embeddings to be similarly interpreted.

Data representation and padding tokens

Each datapoint consists of pairs (token, age) recording the token value and the proband’s age, measured in days from birth, at which the token was recorded. The token vocabulary consists of n = 1,257 different ICD-10 level 3 disease tokens, plus n = 9 tokens for alcohol, smoking and BMI, each represented by three different levels, as well as n = 2 tokens for sex and n = 1 no-event padding token as well as n = 1 additional, non-informative padding token at the beginning or end of the input sequences.

No-event padding tokens were added to the data with a constant rate of 1 per 5 years by uniformly sampling 20 tokens from the range of (0, 36525) and interleaving those with the data tokens after intersecting with the data range for each person. No-event tokens eliminate long time intervals without tokens, which are typical for younger ages, when people generally have fewer diseases and therefore less medical records. Transformers predict the text token probability distribution only at the time of currently observed tokens; thus, no-event tokens can also be inserted during inference to obtain the predicted disease risk at any given time of interest.

Sex tokens were presented at birth. Smoking, alcohol and lifestyle were recorded at the enrolment into the UK Biobank. As this specific time also coincided with the end of immortal time bias (probands had to be alive when they were recruited), smoking, alcohol and BMI tokens times were randomized by −20 to +40 years from this point in time to break an otherwise confounding correlation leading to a sudden jump in mortality rates (and possibly other diseases with high mortality, such as cancers) associated with the recording of these tokens. This probably also diminishes the true effect of these tokens.

Age encoding

Delphi replaces GPT’s positional encoding with an encoding based on the age values. Following the logic frequently used for positional encodings, age is represented by sine and cosine functions of different frequencies, where the lowest frequency is given by 1/365. These functions are subsequently linearly combined by a trainable linear transformation, which enables the model to share the same basis function across multiple encoding dimensions. Another advantage of using age encoding is that Delphi can handle token inputs of arbitrary length, as no parameters are associated with token positions.

Causal self-attention

Standard causal self-attention enables the GPT model to attend to all preceding tokens. For sequential data, these are found to the left of the token sequence. Yet in the case of time-dependent data, tokens can be recorded at the same time with no specified order. Thus, attention masks were amended to mask positions that occurred at the same time as the predicted token. Non-informative padding tokens were masked for predictions of other tokens.

Exponential waiting time model

The input data to Delphi are bivariate pairs (j, t) of the next token class and the time to the next token. Delphi is motivated by the theory of competing exponentials. Let T_i be the waiting times from the current event to one of i = 1, …, n competing events, where n is the number of predictable tokens. Assuming the T_i are each exponentially distributed waiting times with rates λ_i = exp(logits_i), the next event being j is equivalent to T_j being the first of the competing waiting times, that is, T_j = min T_i, or equivalently j = argmin T_i. It can be shown that the corresponding probability is P(j = argmin T_i) = λ_j/Σ_iλ_i, which is the softmax function over the vector of logits. Conveniently, this definition corresponds to the classical cross-entropy model for classification with λ = exp(logits). Thus, Delphi uses a conventional loss term for token classification:

Furthermore, in the competing exponential model the time to the next event T* = min T_j is also exponentially distributed with rate λ* = Σ_iλ_i = Σ_i exp(logits_i). The loss function of exponential waiting times T between tokens is simply a log-likelihood of the exponential distribution for T*:

These approximations hold as long as the rates λ_i are constant in time, which is a reasonable assumption over short periods. For this reason, padding tokens were introduced to ensure that waiting times are modelled over a relatively short period, which does not exceed 5 years in expectation. In line with the tie-braking logic used for causal self-attention, co-occurring events were predicted from the last non-co-occurring token each.

Loss function

The total loss of the model is then given by:

Non-informative padding, as well as sex, alcohol, smoking and BMI, were considered mere input tokens and therefore removed from the loss terms above. This was achieved by setting their logits to -Inf and by evaluating the loss terms only on disease and ‘no event’ padding tokens.

Sampling procedure

The next disease event is obtained through sampling the disease token and the time until the next event. The disease token is sampled from the distribution that originates from the application of the softmax to logits. For the time, samples from all exponential distributions with rates λ_i are taken, and the minimum is retained. Logits of non-disease tokens (sex, lifestyle) are discarded from the procedure to sample disease events only.

Model training

Models were trained by stochastic gradient optimization using the Adam optimizer with standard parameters for 200,000 iterations. The batch size was 128. After 1,000 iterations of warmup, the learning rate was decayed using a cosine scheduler from 6 × 10⁻⁴ to 6 × 10⁻⁵. 32-bit float precision was used.

Model evaluation

Modelled incidence

In the exponential waiting time definition above, the logits of the model correspond to log-rates of the exponential distribution, λ = exp(logit). For example, probability of an event occurring within a year is given by P(T < 365.25) = 1 − exp(−exp(logit) × 365.25).

Age- and sex-stratified incidence

For the training set, age- and sex-stratified incidences were calculated in annual age brackets. The observed counts were divided by the number of individuals at risk in each age and sex bracket, which was given by the number of probands for each sex minus the cumulative number of deaths to account for censoring.

Model calibration

Calibration curves were calculated on the basis of predicted incidences. To this end, all cases of a given token accruing in five year age bins were identified. Subsequently, for all other probands, a control datapoint was randomly selected in the same age band. Predictions were evaluated at the preceding token given that the time difference was less than a year. The predicted incidences were then further grouped log-linearly into risk bins from 10^–6 to 1, with multiplicative increments of log₁₀(5). The observed annual incidence was then calculated as the average of cases and control in age bins, divided by 5 years. The procedure was separately executed for each sex.

AUC for non-longitudinal data

To account for baseline disease risk changes over time, trajectories with disease of interest were stratified into 5 year age brackets from 50 to 80 years, on the basis of the occurrence of the disease of interest. To each bracket, control trajectories of matching age were added. Predicted disease rates were used within each bracket to calculate the AUC, which was then averaged across all brackets with more than two trajectories with the disease of interest. The evaluation was performed separately for different sexes. For some of the analyses, a time gap was used, meaning that for the prediction, only the tokens that were N or more months earlier than the disease of interest were used for the prediction.

Confidence interval estimation for ROC AUC

To estimate the CI for AUC for individual age and sex brackets, we use DeLong’s method, which provides CI mean and variance under the assumption that AUC is normally distributed. As AUC for diseases is calculated as an average of AUC for all brackets, as a linear combination of normal distributions it also is normally distributed with parameters:

where \({\mu }_{i}\) and \({\sigma }_{i}^{2}\) are the mean and variance of AUC for each age and sex bracket, calculated using DeLong’s method.

Quantification of variance between population subgroups

For each disease, we estimated the mean AUC \({\mu }_{s}\) and variance \({\sigma }_{s}^{2}\) for each subgroup using DeLong³⁹ method. Under the null hypothesis that all subgroups have the same true AUC (no bias), any observed differences would be attributable to statistical variance.

We use a two-level testing approach: (1) individual subgroup testing: for each disease–subgroup combination, we calculate standardized residuals by subtracting the weighted mean AUC across all subgroups from the subgroup-specific AUC and dividing by the s.d.:

Under the null hypothesis, these standardized residuals should follow a standard normal distribution. We identify outliers using a two-sided Bonferroni-corrected significance threshold.

(2) Disease-level testing: for each disease, we sum the squared standardized residuals across all subgroups:

Under the null hypothesis, this sum follows a χ² distribution with degrees of freedom equal to (n − 1), where n is the number of subgroups. We identify diseases with excessive between-subgroup variance using a one-sided Bonferroni-corrected significance threshold.

Owing to limitations of DeLong’s method with small sample sizes, in each disease–subgroup combination, we filtered age and sex brackets with fewer than six cases and diseases with less that two brackets remaining after filtering. We also excluded diseases that had fewer than two subgroups presented.

Incidence cross-entropy

To compare the distribution of annual incidences of model and observed data, a cross-entropy metric was used. Let p_i be the annual occurrence of token i in each year. thus, the age- and sex-based entropy across tokens is given H(p,q) = −p × log(q) − (1 − p) × log(1 − q). For low incidences p and q, the latter term is usually small. The cross-entropy is evaluated across all age groups and sexes.

Generated trajectories

To evaluate the potential of generating disease trajectories, two experiments were conducted using data from the validation cohort. First, trajectories were generated from birth using only sex tokens. This was used to assess whether Delphi-2M recapitulates the overall sex-specific incidence patterns. Second, all available data until the age of 60 were used to simulate subsequent trajectories conditional on the previous health information. A single trajectory was evaluated per proband. Trajectories were truncated after the age of 80 as currently little training data were available beyond this point. Incidence patterns were evaluated as described above.

Training of linear models with polygenic risk scores, biomarkers and overall health rating status

We trained a family of linear regression models on the task of predicting 5-year disease occurrence. All models were trained on the data available at the time of recruitment to the UK Biobank, using different subsets of the following predictors:

• Polygenic risk scores (UKB Category 301)

• Biomarkers (as used in the MILTON paper, biomarkers with more than 100,000 missing values in UKB excluded, imputed with MICE)

• Overall health rating (UKB field 2178)

• Delphi logits for the disease of interest

Moreover, all models had sex and age information included.

To evaluate the performance of the models, we used the same age- and sex-stratified AUC calculation that we used for Delphi performance evaluation. For breast cancer, only female participants were included. For E10 insulin-dependent diabetes mellitus, we masked all other diabetic diseases (E11–E14) from Delphi inputs when computing logits.

Model longitudinal evaluation

Study design

To validate the predictions of the model, we also perform a longitudinal test, internally for the UK Biobank data and externally on the Danish health registries. This has two advantages: (1) we can enforce an explicit cut-off and separate data to avoid any potential time-leakage; and (2) we obtain insights into Delphi-2M prognostic capabilities and generalization.

However, as mentioned in the data splits, we use two different cut-off dates between the two data sources, mainly due to differential data availability, the principal setup applies to both in the exact same way.

We collate data up to a specific cut-off date for each individual and use Delphi-2M to predict an individual’s future rate across all disease tokens. Building on the exponential waiting time representation, we obtain rates over a 1 year time frame. The preceding year after the cut-off date is discarded to introduce a data gap. Subsequently the incidence in the next year is used for evaluation. Predictions are made for individuals 50–80 years of age.

Algorithms for comparison

We build a standard epidemiological baseline based on the sex- and age-stratified population rates. These are based on the Nelson–Aalen estimator^40,41, a nonparametric estimator of the cumulative hazard rate, across all diseases. For the UK Biobank, the estimators are based on the same training data as Delphi-2M. For the Danish registries, we use the entire Danish population in the time period from 2010 to 2016.

As the UK Biobank contains a wide range of phenotypic measures, we also estimate clinically established models and other machine learning algorithms for comparison.

We evaluate the models on cardiovascular disease (CVD) (ICD-10: I20–25 I63, I64, G45), dementia (ICD-10: F00, F01, F03, G30, G31) and death.

For CVD we compare against: QRisk3 (ref. ⁴²), Score2 (ref. ⁴³)(R:RiskScorescvd:SCORE2)⁴⁴, Prevent^45,46 (R:preventr)⁴⁷, Framingham^11,46,48 (R:CVrisk:10y_cvd_frs)¹¹, Transformer, AutoPrognosis v2.0 (ref. ⁴⁹) and LLama3.1(8B)⁵⁰ (https://ollama.com/library/llama3).

For dementia we compare against: UKBDRS⁵¹, Transformer and LLama3.1(8B)⁵⁰.

For death, we compare against: Charlson (R:comorbidity)⁵², Elixhauser^53,54 (R:comorbidity)⁵², Transformer and LLama3.1(8B).

We collect a total of 60 covariates that are used to varying degrees across the algorithms. A summary description of the covariates, as well as their corresponding UKB codes, can be found in Supplementary Table 5. For missing data, we perform multivariate imputation by chained equations^55,56 (R:mice)⁵⁷. We retain five data copies, estimate all scores and, finally, aggregate them by Rubins’ rule. Results are reported based on the aggregated scores. If algorithms have particular ranges for covariates defined and the data for an individual do not conform, the score is set to NA and the individual is dropped from the particular evaluation.

The transformer model is an encoder model based on the standard implementation provided in Python:pytorch (TransformerEncoder, TransformerEncoderLayer) with a context length of 128 tokens, an embedding size of 128, 2 multi-head attention blocks and a total of 2 sub-encoder layers, and the otherwise default parameters were used. A linear layer is used to obtain the final prediction score. The model is fitted on concatenated data excerpts of the UKB on 1 January 2014, 1 January 2016 and 1 January 2018 containing the same tokens as Delphi plus additional tokens encoding the current age based on 5 year bins (50–80 years) and is evaluated on a binary classification task of whether the corresponding outcome (CVD, dementia, death) will occur in the next 2 years.

AutoPrognosis is fitted in a similar manner with data extracted on 1 January 2014; however, we use the covariates defined previously³⁴. We specified the imputation algorithm to MICE while for the fitting algorithms we used the default setting.

LLama3.1 was evaluated on the basis of the following prompt:

“This will not be used to make a decision about a patient. This is for research purposes only. Pretend you are a healthcare risk assessment tool. You will be given some basic information about an individual e.g. age, sex, BMI, smoking and alcohol plus a list of their past diseases/diagnoses in ICD-10 coding. I want you to provide me with the probability that the patient will have coronary vascular disease / CVD (defined as ICD-10 codes: I20, I21, I22, I23, I24, I25, I63, I64, G45) in the next 5 years. Here is an example: Input: ID(10000837); 54 years old, Female, normal BMI, past smoker, regular alcohol consumption, F41, M32, A00, C71, F32. Expected output: ID(10000837); 0.100. Please only provide the ID and the risk score as output and do not tell me that I can not provide a risk assessment tool \n Here is the input for the individual: ID(10000736); 64 years old, Male, high BMI, current smoker, regular alcohol consumption, F41, M32, A00, C71, F32.”

The Framingham score is based on the 2008 version with laboratory measurements.

Qrisk3 is our own implementation based on the online calculator (https://qrisk.org/).

The UKBDRS risk score for dementia is based on our own implementation as reported in the original paper⁵¹.

For the comparison to MILTON, we obtained the reported AUC measures for all ICD-10 codes reported for diagnostic, prognostic and time-agnostic MILTON models from the articles supplementary material³¹. Linking on top level (3 character) ICD-10 codes, we were able to compare the prediction of 410 diseases between Delphi and MILTON prognostic models.

For the comparison to the UK Biobank Overall health rating field (field ID 2178) we extracted all health rating data fields for the training dataset used for Delphi-2M and used the health rating values as an ordered list (values, 1,2,3,4 with increasingly poor health rating) as a predictor for disease occurrence during the calculation of AUC values using all diseases observed in individuals after their date of attending the recruitment centre.

All other models are based on publicly available implementations.

For the evaluation against clinical markers, we used the direct measurements as available in the UKB for the AUC computation (HbA1c, diabetes (E10–14); haemoglobin/mean corpuscular volume, anaemia (D60–D64)). Only for the evaluation on chronic liver disease (K70–77), we used the predictions from a logistic regression model with alkaline phosphatase, alanine aminotransferase, gamma-glutamyltransferase, total protein, albumin, bilirubin and glucose as covariates. Evaluations are based on a 5-year time window after an individual’s recruitment data.

The Charlson and Elixhauser comorbidity index is based on the same data as Delphi; however, the Charlson comorbidity index is originally based on ICD-10 level 4 codes. We therefore estimate based on a version that maps the level 3 codes to all possible level 4 codes. We estimated a version with the level 3 codes as well and this did perform marginally worse.

Overall, we tried to model the data as close as possible to the originally used covariates; however, in some places, small adjustments were made. Particularly, we retain only level 3 ICD-10 codes; thus, definitions based on level 4 codes are approximated by their level 3 codes.

Performance measures and calibration

To assess the discriminatory power of the predicted rates for the longitudinal test, we use the area under the receiver operating curve (ROC-AUC) and the average precision-recall curve (APS) as implemented in Python:scikit-learn. Thus, we compare the observed cases in the evaluation period against the predicted scores obtained at the respective cut-off date. All diseases with at least 25 cases were assessed.

Furthermore, we compare the predicted rates from Delphi-2M to the observed incidence to determine the calibration of the predicted rates using Python:scikit-learn. Delphi-2M predicted rates are split into deciles, and for each bin, we compare Delphi-2M’s average rate against the observed rate within the bin. We include all diseases with at least 25 cases.

Model interpretation

Token embedding UMAP

The low-dimensional representation of token space was constructed by applying the UMAP⁵⁸ dimensionality reduction algorithm to the learned token embeddings for Delphi-2M (1,270 × 120 matrix). The cosine metric was used.

SHAP

To evaluate the influence of each token in a trajectory on the next predicted token, we adopted the SHAP methodology. Each trajectory from the validation cohort was augmented by masking one or several tokens and then used for prediction. The change of logits after many such augmentations was aggregated by a PartitionExplainer from the SHAP Python package.

Masking procedure

The number of augmentations for each trajectory was determined using the PartitionExplainer masking algorithm. When masked, tokens were replaced by a ‘no event’ placeholder that was also used during training. Sex tokens, when masked, were replaced with the corresponding token of the opposite sex.

SHAP values evaluation

The described procedure was applied to each of 100,639 trajectories in the validation cohort. The predicted token was always the last available token in the trajectory.

Cox hazard ratios

To assess the interpretation of the SHAP values, we use a penalized time-dependent Cox model, developed for use with EHR data¹⁵, and compare the corresponding hazard estimates to our averaged SHAP values.

Nonparametric hazard ratios

To complement the SHAP analysis and the assessment of Delphi-2M’s modelling of time-dependent effects, we also performed an evaluation based on the Nelson–Aalen estimator. For a given token, we identify individuals with the token and estimate their corresponding cumulative hazard from the occurrence of the token onwards. Moreover, we randomly select five age–sex-matched individuals for each case and estimate the cumulative hazard in this comparison group. We can then obtain an estimate of the hazard rate by taking the derivative of the cumulative hazard. We apply a Gaussian kernel to acquire a smooth estimate. Subsequently, we can take the ratio of the two hazards and obtain a crude nonparametric estimate for the hazard ratio of the token over time.

Generative modelling

Training on synthetic data

The model was trained on simulated trajectories sampled from Delphi-2M. The dataset size was 400,000 trajectories, the same as for the original training set. The trajectories were samples from birth; sex was assigned randomly. No training hyperparameters were changed compared to Delphi-2M.

Statistics and reproducibility

Validation on external datasets

No novel data were generated for this study. Reproducibility of the method has been confirmed by retraining Delphi-2M using different train-validation splits (n = 4 independent experiments; Supplementary Fig. 1) and testing the trained model using longitudinal UK Biobank data and external data from the Danish National Patient Registry.

Ethics approval

The UK Biobank has received approval from the National Information Governance Board for Health and Social Care and the National Health Service North West Centre for Research Ethics Committee 532 (ref: 11/NW/0382). All UK Biobank participants gave written informed consent and were free to withdraw at any time. This research was conducted using the UK Biobank Resource under project 49978. All investigations were conducted in accordance with the tenets of the Declaration of Helsinki.

The use of the Danish National Patient Registry for validation of the UK Biobank results was conducted in compliance with the General Data Protection Regulation of the European Union and the Danish Data Protection Act. The analyses were conducted under the data confidentiality and information security policies of the Danish National Statistical Institute Statistics Denmark. The Danish Act on Ethics Review of Health Research Projects and Health Data Research Projects (the Committee Act) do not apply to the type of secondary analysis of administrative data reported in this paper.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.