Proximity screening greatly enhances electronic quality of graphene

Device fabrication

The devices were fabricated using the standard van der Waals assembly and electron-beam lithography, following procedures established in the literature without introducing critical modifications. Our detailed protocols are provided in Supplementary Information and summarized below.

Monolayer graphene, hBN crystals (both 30–70 nm thick and 3–4 layers thin) and relatively thick graphite (5–50 nm) were mechanically exfoliated onto an oxidized Si wafer (290 or 70 nm SiO₂). Their thicknesses were determined using optical contrast, atomic force microscopy and Raman spectroscopy (Supplementary Information). For most of the reference devices with remote graphite and Si gates, we assembled the exfoliated crystals using polymer-free flexible silicon nitride membranes¹⁷. For all proximity-gated devices and some reference devices, we employed polydimethylsiloxane stamps with polypropylene carbonate as a sacrificial layer. Although not critical, we found the latter method preferable for proximity-gated devices as it imposes fewer constraints (Supplementary Information).

We began the assembly of encapsulated graphene by picking up a selected top hBN crystal and then using it to sequentially collect graphene and bottom hBN crystals. Crucially for achieving ultrahigh electronic quality, the stacking process required the slow deposition of two-dimensional crystals onto each other, as this minimized the formation of bubbles and wrinkles and, consequently, allowed the sufficiently large final devices (Supplementary Fig. 1). All assembly procedures were conducted in air. Exfoliated flakes were either used within an hour or stored in a glovebox for assembly within 2–3 weeks. The completed trilayer stacks were transferred onto either a graphite crystal (for graphite-gated devices) or an oxidized Si wafer.

Following the assembly, we used electron-beam lithography to define the top gate region and we deposited Cr–Au metallization by electron-beam evaporation. In the subsequent lithography step, we created electrical contacts by first exposing graphene edges using reactive-ion etching and then depositing Cr–Au to form one-dimensional contacts. The typical contact resistance was 2–5 kΩ µm at the neutrality point and decreased down to 0.1–0.3 kΩ µm at high doping. In the final step, we used the metallic top gate as an etching mask and defined multi-terminal Hall bars, as shown in the micrographs throughout the main text, Methods and Supplementary Information.

Although some devices failed during fabrication (typically because of poor one-dimensional contacts), all successfully fabricated proximity-gated devices demonstrated consistently ultrahigh quality, with SdH oscillations always emerging below 4–5 mT and sometimes below 1 mT. The primary determinants of our device quality were interface cleanliness and careful, slow stacking (as described above and detailed in Supplementary Information).

Electrical measurements

Magnetotransport measurements were carried out in two cryogenic systems. A liquid-He cryostat with a variable temperature insert was used to study transport from 1.7 K up to room T. For measurements in the fractional QHE regime, we used a dilution refrigerator (Oxford Instruments) with T from 6 K down to 50 mK and magnetic fields up to 12 T.

For resistance measurements, we used the standard low-frequency lock-in technique at 30.5 Hz. Typically, the a.c. currents were between 1 and 5 nA, which allowed us to avoid heating and self-gating effects. Higher currents were required in magneto-focusing and bend-resistance experiments to achieve sufficient signal-to-noise ratios: up to 1 µA for devices with remote gates and up to 0.1 µA for proximity-gated devices.

To control the carrier density n, we applied gate voltages using a Keithley Sourcemeter-2636B. For proximity-gated devices, in most cases we used only the top Au gate while keeping the bottom graphite or Si gate grounded. This approach prevented tunnelling through and possible breakdown of the few-layer hBN dielectric between the graphene and the proximity gate. However, for measurements of the fractional QHE, we found it advantageous to use the proximity gate to vary n. This strategy allowed us to avoid insulating QHE states inside the graphite gate (due to the 2.5-dimensional QHE in graphite³⁶). Simultaneously, we applied a large bias to the bottom Si gate to suppress insulating states in regions of the graphene electrical leads that were not covered by the graphite gate.

Converting gate voltages into carrier density

For devices with relatively thick gate dielectrics, the carrier density n in graphene exhibits a practically linear dependence on gate voltage V_g because the geometric capacitance dominates (approximately 12 nF cm⁻² for our Si-gated devices). The linearity holds because typical shifts in the chemical potential of graphene are small compared with eV_g. However, the simple relation n ∝ V_g breaks down notably in proximity-gated devices with their ultrathin dielectrics, as high-quality graphene exhibits a vanishingly small density of states near the neutrality point and in quantizing magnetic fields. This phenomenon is conventionally described in terms of quantum capacitance C_q = e∂n/∂µ, which contributes in series with the geometric capacitance and consequently dominates if the density of states and, hence, C_q become sufficiently small^37,38. The resulting nonlinearities in the n(V_g) dependence become particularly pronounced in ultrahigh-quality graphene, as elucidated by Extended Data Fig. 1. Below we describe our methodology for converting the gate voltage into a carrier density.

We modelled our devices as parallel-plate capacitors with top and bottom gates biased at V_t and V_b (bottom panel of Extended Data Fig. 1a). The gates were separated from the graphene by hBN layers of thicknesses d_b and d_t. Applied voltages created electric fields E_t and E_b inside the top and bottom hBN dielectrics. V_t shifted the electrostatic potential by d_tE_t and, therefore, changed the electrochemical potential of graphene µ(n), yielding the equation eV_t = ed_tE_t + µ(n) where e denotes the absolute value of the electron charge. Similarly for the bottom gate, eV_b = ed_bE_b + µ(n). The charge densities at the gate interfaces were n_t = −εε₀E_t/e and n_b = −εε₀E_b/e where ε₀ is the vacuum permittivity and ε ≈ 3.5 is the hBN dielectric constant. Charge conservation requires n_t + n_b + n = 0, which yields the following equation connecting n and µ with the gate voltages:

This equation is generally applicable to any double-gated field-effect device that uses a two-dimensional material as a conducting channel. In most of our measurements, we used only the top gate to vary n while keeping both graphene and the proximity (bottom) gate grounded (V_b = 0). It is important to note that, according to the above equations, electric fields will still develop in the gate dielectrics, even when the graphene is electrically connected to one of the gates, provided the other gate shifts µ(n) from zero. Indeed, if V_b = 0, we obtain E_b = −µ(n)/ed_b, which shows that, despite being grounded, the proximity gate with its ultrathin dielectric actively participates in the device electrostatics and, as E_b ∝ 1/d_b, strongly contributes to the nonlinear behaviour of n(V_t).

The electrochemical potential µ(n) in equation (1) can be calculated by numerically inverting the integral:

where f(E, µ, T) is the Fermi–Dirac distribution function. The density of states D(E) is modelled in graphene as

This equation is written for the general case of a finite magnetic field. Here, E_i is the energy of the ith Landau level, and D(E) depends not only on energy E but also on magnetic field B and level broadening Γ due to both temperature and disorder^37,38. We solved equation (1) numerically (using an energy cutoff of 0.5 eV in all computations). Examples for non-quantizing and quantizing fields are illustrated in Extended Data Fig. 1a by black solid curves.

Experimentally, we determined the carrier density n as a function of V_t by measuring the Hall resistivity ρ_xy(V_t) at zero V_b and employing the standard expression n = B/eρ_xy. The latter is valid only outside the mixed electron–hole regime near the neutrality point (see, for example, Extended Data Fig. 3a and ‘Charge inhomogeneity from Hall measurements’ in Methods), which resulted in gaps on our experimental curves for very low n ≲ δn (Extended Data Fig. 1a). For the known thicknesses d_b and d_t, we fitted our experimental data using the numerical model described above, with broadening Γ as the only fitting parameter. Extended Data Fig. 1a shows good agreement between the experimental n(V_t) dependences and the model, yielding Γ ≈ 0.25 meV. This shows that, for the presented device, the energy broadening was dominated primarily by T. Our model accurately described the experimental curves in both non-quantizing and quantizing fields (left and right panels, respectively). We applied these fitted dependences (using the Γ values determined for each device) to convert V_t into n and present the experimental data for proximity-gated devices as a function of n for different B and T.

We assessed the accuracy of our conversion procedure by examining how well it describes the ρ_xx peak positions on the Landau fan diagram measured over a wide range of V_t and B (Extended Data Fig. 1b). For monolayer graphene in moderate B, these peaks should appear at filling factors ν = 0, ±4, ±8, ±12, … and follow the immutable relation B(ν) = nh/eν on the fan diagram. Using our model with the extracted Γ values, we calculated n(V_t) and used this to determine the B(V_t) dependences for different filling factors, as shown by dashed curves in Extended Data Fig. 1b. The excellent agreement between measured and predicted Landau-level positions confirms the accuracy of our procedure for converting gate voltages into carrier densities. Using the same procedure, we transformed the nonlinear fan diagrams obtained as functions of V_t (such as shown in Extended Data Fig. 1b) into the standard fan diagrams where Landau levels appear as straight lines radiating from the origin, as required by theory (Fig. 3 and Extended Data Fig. 6). These linear fan diagrams provide further confirmation of the accuracy of our approach.

Charge inhomogeneity in the best remote-gated devices

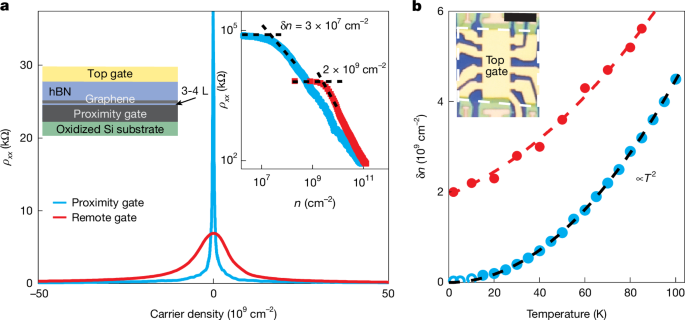
In the main text, we compared our proximity-gated devices with reference devices that used remote graphite gates. Extended Data Fig. 2 provides further details about our best remote-gated device. Its zero-B resistivity ρ_xx(n) near the neutrality point is shown for two representative T (Extended Data Fig. 2a) and replotted on a log–log scale so that we could evaluate the residual charge inhomogeneity δn (Extended Data Fig. 2b). With increasing T, the resistivity peak broadened because of thermally excited carriers. The extracted δn(T) is shown in Extended Data Fig. 2c. Above 150 K, the experimental data follow the expected parabolic dependence δn = n_th(T)/2 ∝ T² within our measurement accuracy, as discussed in the main text. Below 10 K, δn saturates because electron–hole puddles dominate the transport properties.

Charge inhomogeneity from Hall measurements

An alternative way to evaluate the charge inhomogeneity δn is to use Hall measurements¹⁸. Extended Data Fig. 3a shows ρ_xy(n) for one of our proximity-gated devices at two representative T. The density range between the extrema in ρ_xy(n) marks the regime of mixed electron–hole transport where the Hall response no longer follows the standard single-carrier dependence ρ_xy(n) = eB/n. The distance between the extrema is given by n_th ≈ 2δn and provides another quantitative measure of charge inhomogeneity¹⁸. On increasing T from 10 to 40 K, the extrema moved apart and broadened. Extended Data Fig. 3b compares the extracted δn with that expected from thermal excitations at the neutrality point. Above 10 K, δn follows the parabolic dependence n_th(T)/2 ∝ T² (within measurement accuracy), matching the results from the broadening of the ρ_xx(n) peak shown in Fig. 1c.

Metal–insulator transition

At low T, our proximity-gated devices exhibited a highly resistive state at the neutrality point, which showed signatures of strong localization and quantum interference. Extended Data Fig. 4a is a plot of ρ_xx(n) under zero B. There is a pronounced peak at the neutrality point, which reached approximately 100 kΩ at 0.5 K, that is, 5 times larger than expected for charge-neutral ballistic graphene in its minimum conductivity state³⁹. This behaviour indicates a metal–insulator transition, probably of Anderson type, as previously observed in double-layer graphene heterostructures⁴⁰. The resistivity overshoots the maximum metallic value³⁹ of πh/4e² ≈ 20 kΩ at n ≲ 10⁸ cm⁻². This corresponds to the Fermi wavelength λ_F ≳ 3.5 µm, which becomes comparable to the device width W. In this regime, the number of electronic channels fitting W is reduced to less than 5, whereas the Fermi energy is only 10–15 K. Under these conditions, quantum confinement effects become significant and open energy gaps between quantized sub-bands, which can become comparable to k_BT. The onset of spatial quantization could contribute to the observed insulating state, although Anderson-type localization is probably the dominant mechanism given the observed B and T dependences⁴⁰. Away from the neutrality point, other ‘mesoscopic’ features appeared on the ρ_xx(n) curves at subkelvin T (Extended Data Fig. 4a). Given the long λ_F, these features can be attributed to interference (Fabry–Pérot) resonances caused by standing waves in our ballistic devices.

To elucidate the nature of the observed insulating state, we analysed the T dependence of resistivity at the neutrality point (ρ_NP). Extended Data Fig. 4c shows an example of the measured ρ_NP(T). The same data are replotted in Arrhenius coordinates in Extended Data Fig. 4b. The complete evolution of ρ_xx(n) with T is presented in Extended Data Fig. 4d. These plots rule out the presence of simple thermal activation over an energy gap at the Dirac point, which would manifest as a straight line in the Arrhenius plot. Instead, ρ_NP(T) has two distinct regimes: (1) logarithmically increasing with decreasing T below 10 K (black dashed curve in Extended Data Fig. 4c) and (2) a 1/T dependence at higher temperatures (red curve). The 1/T behaviour can be understood as follows. The density of thermally excited electrons and holes at the Dirac point is given by n_th ∝ T² (Fig. 1c), whereas their effective masses m_th ∝ T (refs. ^18,25). Consequently, the observed dependence ρ_NP ∝ 1/T implies a temperature-independent scattering time, τ = m_th/(e²n_thρ_NP), consistent with the ballistic transport of Dirac fermions limited by edge scattering and τ ≈ W/v_F, as discussed in the main text.

The magnetic field dependence provides further insight into the metal–insulator transition. Extended Data Fig. 4e shows ρ_NP(B) at 2 K. The insulating state was suppressed by fields of approximately 1 mT, resulting in pronounced negative magnetoresistance. We attribute this suppression to the breaking of time-reversal symmetry for interfering electron trajectories, a mechanism analogous to the destruction of weak localization in normal metals and which is expected to play a role in strong (Anderson-type) localization¹⁸. On increasing T above 10 K, the magnetoresistance changed sign from negative to positive, as evident from comparing ρ_NP(T) at 0 and 5 mT in Extended Data Fig. 4f. This positive magnetoresistance is characteristic of a charge-neutral Dirac plasma in the Boltzmann regime²⁵. The sign change occurs at approximately 10 K, providing independent confirmation of the regime change from the insulating state to the ballistic Dirac plasma, which was inferred above from changes in the functional form of ρ_NP(T) (Extended Data Fig. 4c). The negative magnetoresistance also rules out an excitonic gap at the Dirac point. If present, such a gap would be enhanced by the magnetic field due to stronger confinement and increased exciton binding energy, contrary to our observations.

Magnetic focusing in reference devices

Extended Data Fig. 5a,b presents magneto-focusing measurements for hBN-encapsulated graphene devices with a Si-wafer gate (approximately 350 nm below the graphene) and a graphite gate (approximately 70 nm below), which are analogous to the measurements in Fig. 2 for proximity-gated devices. The focusing peaks appear at the expected positions given by^26,27 B(n,P) = 2ħ(πn)^1/2P/eL where P is the peak number and L the distance between injector and collector (dashed curves in Extended Data Fig. 5a,b).

We define the ‘first appearance’ of magneto-focusing peaks as the carrier density n where the P = 1 peak becomes clearly distinguishable above a noisy or fluctuating background, typically exceeding it by a factor of over 2. Importantly, the peak grows very rapidly as a function of n, so that the exact threshold factor is relatively unimportant and, in our experience, led to variations of less than 30% in the estimated onset density. Using this criterion, the magneto-focusing peaks in Extended Data Fig. 5a,b first appeared at n ≈ 0.5 and approximately 0.1 × 10¹² cm⁻² for the devices with Si and remote graphite gates, respectively. For the measurement geometries shown in the figure insets with injector–collector separations L ≈ 19 and 22.5 μm, this yielded transport mobilities µ = (eℓ/ħ)(πn)^−1/2 ≈ 2 and 7 × 10⁶ cm² V⁻¹ s⁻¹, respectively. These values are in good agreement with the mobilities extracted from the ρ_xx(n) dependences of the devices at the same densities, which validates the criterion suggested for estimating transport mobilities from the appearance of the first peak in magneto-focusing measurements. Accordingly, we have used this criterion to estimate µ also in proximity-gated devices. The surprising accuracy of this rule-of-thumb criterion stems from the very rapid development of magneto-focusing signals with increasing n, which resembles the similarly simple criterion for estimating the quantum mobility as discussed in ‘Determination of quantum mobility’ in Methods.

Extended Data Fig. 5c summarizes our findings for mobility in all three types of device. Remote graphite gates improve µ several fold compared to Si-gated devices (which explains why graphite gates have become common in the recent literature), whereas proximity screening provides another order-of-magnitude enhancement in electronic quality. Note that the achieved mobilities in Extended Data Fig. 5c have to be compared at different carrier densities because magnetic focusing became observable only at n that exceeded δn by 30–100 times, with δn varying significantly between device types.

Onset of SdH oscillations

We studied seven graphene devices with proximity gates, and results for three of them with remnant δn < 10⁸ cm⁻² are presented below. Extended Data Fig. 6 shows their Landau fan diagrams near the neutrality point, along with horizontal cuts at several fields in the millitesla range. Quantization becomes clearly visible below 1, 2 and 3 mT for devices S2, S3 and S4, respectively, so that µ_q exceeded 10, 5 and 3.3 × 10⁶ cm² V⁻¹ s⁻¹, respectively. The quantum mobility in device S2 matched or exceeded that of device S1, as described in the main text. To ensure reliable identification of SdH oscillations, we considered them to emerge only if the resistivity minima at ν = ±2 became pronounced enough to rule out any possible quantum-interference features (main text and ‘Metal–insulator transition’ in Methods). This required fields notably higher than those needed for the criterion µ_qB* ≈ 1, where SdH oscillations with amplitude less than exp(−π) ≈ 4% of total ρ_xx appear at B* (‘Determination of quantum mobility’ in Methods). Accordingly, the above values provide only lower bounds for µ_q.

Determination of quantum mobility

Although the expression µ_qB* ≈ 1 is widely adopted in the literature, to justify its use in our study, we performed a quantitative analysis of SdH oscillations. To avoid complications arising from the metal–insulator transition, QHE and interference resonances, the measurements were carried out on devices with remote graphite gates at an elevated T of 5 K. Under these conditions, the SdH oscillations exhibited clear sinusoidal behaviour, with their amplitude exponentially increasing with B (examples are shown in Extended Data Fig. 7a).

To analyse such curves, we applied the Lifshitz–Kosevich formula⁴¹

where ω_c is the cyclotron frequency. For each carrier density, we replotted the oscillatory part of the resistivity Δρ_xx as a function of 1/B and fitted it using the Lifshitz–Kosevich expression, with µ_q as the only fitting parameter (inset of Extended Data Fig. 7b). Extended Data Fig. 7b compares the quantum mobilities extracted from these fits with those obtained using the rule-of-thumb criterion µ_qB* ≈ 1 with B* being the field at which SdH oscillations first become clearly discernible (empty diamonds in Extended Data Fig. 7a). Within our experimental accuracy (10–20%), the two methods yield identical values of µ_q, validating our use of the simpler criterion.

Onset of quantized Hall plateaux

Although in our proximity-gated devices quantum Hall plateaux appeared in fields as small as several millitesla, we found that contact geometry, rather than disorder, limited QHE onset. Extended Data Fig. 8a shows the Hall resistivity ρ_xy(n) at different magnetic fields. As B was increased, the peaks of ρ_xy grew until they reached the quantized value of h/2e² at 4–5 mT. At these fields, the cyclotron diameter D_c was comparable to the width w of our voltage probes (for Dirac fermions at ν = ± 2, D_c = 2ℓ_B ≈ 1.6 µm/B(mT)^1/2). Consequently, cyclotron orbits at lower B were reflected, preventing edge states from reaching the contact regions and, thus, destroying the quantization²⁹.

To corroborate this geometric effect, we examined QHE onset in devices with different w. Extended Data Fig. 8b plots the onset field versus w (blue symbols). Hall plateaux developed systematically at lower B for wider contacts, following qualitatively the criterion D_c ≲ w. This indicates that, in our proximity-gated devices, the onset of full quantization was still limited by the dimensions of the voltage probe rather than the homogeneity of graphene or mobility, and we expect the QHE in proximity-gated devices to fully develop in fields as low as 1 mT, if we use contacts wider than 2 μm.

Fractional QHE under proximity screening

To assess how the fractional QHE develops in our proximity-gated devices, we studied in detail its evolution with increasing B, as shown in Extended Data Fig. 9. No fractional states could be observed below 6 T. Their signatures at ν = 2/3 and 5/3 first appeared above 7 T and became more pronounced at higher fields (Extended Data Fig. 9a,b). Notably, no signatures of ν = 1/3 were observed in any of our devices, which we attribute to the large negative quantum capacitance, which increases the total capacitance near incompressible states and can lead to a complete collapse of visible gaps when measurements are performed as a function of gate voltage³¹.

The emergence of fractional states corresponds to the magnetic length ℓ_B decreasing below 10 nm. This is consistent with the fact that ℓ_B represents the spatial scale of electron–electron interactions responsible for the fractional QHE. This critical scale of 10 nm inferred from the emergence of fractional states at 7 T aligns well with the characteristic scale 2παd ≈ 10 nm at which proximity screening for d ≈ 1 nm becomes effective in suppressing electron–hole puddles, as discussed in the main text. The systematic appearance of fractional QHE states only when ℓ_B < 10 nm confirms that proximity screening primarily affects long-range interactions while preserving the short-range ones essential for many-body phenomena in high magnetic fields.

Sources of disorder

Despite considerable progress in improving the quality of graphene devices over the past decade, the primary sources of disorder limiting mobility and charge homogeneity in hBN-encapsulated graphene remain poorly understood. Our current experiments and the existing literature allow us to rule out several potential disorder sources. First, atomic-scale defects in the graphene itself or at graphene/hBN interfaces are unlikely to be the dominant scatterers. Scanning probe experiments would have revealed individual short-range defects that were clearly visible on the corresponding images⁴² and did not occur within areas as large as over 10 µm². Graphene/hBN interfaces are known to be atomically clean and flat, with minimal interfacial contamination⁴³ (except for bubbles and wrinkles, which, however, were absent in our devices; Supplementary Information). Second, charged impurities at the metal/hBN interface of the top gate also appear to play a minimal role. Further experiments demonstrated no significant improvement when using graphite for both top and bottom gates (placed at distances of more than 10 nm). The latter observation is in line with previous studies using double-gated devices with two graphite gates, which found that mobilities were comparable to those in our remote-graphite-gated devices. Furthermore, attempts to use other atomically flat metallic crystals as proximity gates (including Bi₂Sr₂CaCu₂O_8+x and TaS₂) failed to yield high mobilities²¹, presumably due to charged impurities in contact with hBN at their surfaces. Third, elastic strain in graphene can generate electron–hole puddles, but our observations indicate this to be an improbable primary source of disorder. Indeed, strain-induced puddles cannot be suppressed by proximity gating, yet we observed a notable reduction in the charge inhomogeneity.

Beyond edge scattering, which obviously dominates in our limited-width devices, charged impurities within hBN represent the most probable source of both residual disorder and charge inhomogeneity. The hBN crystals used in our devices (from the National Institute for Materials Science) contain impurities at concentrations of approximately 10¹⁵ cm⁻³, primarily carbon substituents (T. Taniguchi, private communication). In comparison, state-of-the-art GaAlAs heterostructures^8,9 contain impurities at concentrations of less than 5 × 10¹³ cm⁻³. However, this comparison requires nuanced interpretation. Impurities in hBN typically lie deep within the bandgap and remain predominantly neutral, whereas impurities in GaAlAs heterostructures (such as Si used for doping) are mostly ionized. Nonetheless, it is plausible that a fraction of deep impurity states in hBN become charged, creating a background electrostatic potential in graphene. The observed effectiveness of proximity gating (particularly in suppressing charge inhomogeneity by two orders of magnitude) strongly supports this interpretation. Proximity screening specifically targets long-range electrostatic disorder while having a minimal impact on short-range scattering mechanisms. Although this analysis provides useful insights, a definitive conclusion about the dominant source(s) of disorder in hBN-encapsulated graphene demands further systematic investigation. This will probably require larger devices, as the mobilities achieved in our proximity-gated devices have been limited by edge scattering due to their finite size.

Helical quantum Hall transport

Although proximity screening suppresses electron–electron interactions, it can enable quantum phases that are otherwise difficult to observe in remote-gate devices. A notable example is the helical quantum Hall phase in the zeroth Landau level, which arises if a spin-polarized ferromagnetic phase is stabilized either by very large in-plane magnetic fields (approximately 30 T)⁴⁴ or by screening Coulomb interactions using high-ε substrates³⁵. In standard graphene devices, the zeroth Landau level typically exhibits an antiferromagnetic ground state, resulting in an insulating bulk and insulating edges. By contrast, the ferromagnetic phase leads to a quantum Hall topological insulator with an insulating bulk but conducting helical edge channels where the current propagation direction is locked to electron spin polarization^35,44 (Extended Data Fig. 10a).

To test for helical edge transport in proximity-gated graphene, we measured the two-terminal conductance in different contact configurations under a perpendicular magnetic field. In our multi-terminal Hall bar geometry, each ohmic contact acts as an equilibration reservoir for counter-propagating edge states, and therefore, each edge section between two contacts represents an ideal helical quantum conductor with resistance h/e². Considering conduction along both device edges, the two-terminal conductance can be written as G_2t = (e²/h)(N_R⁻¹ + N_L⁻¹), where N_R and N_L are the numbers of helical-conductor sections for the right and left edges, respectively (Extended Data Fig. 10a, right panel).

Extended Data Fig. 10b shows the measured two-terminal conductance versus top gate voltage V_t at B = 80 mT, a relatively small but sufficient field for suppressing the insulating state at the neutrality point (‘Metal–insulator transition’ in Methods). As expected, well-defined conductance plateaux appeared at 2e²/h and 6e²/h, corresponding to the filling factors ν = ±2 and ν = ±6, respectively. Additionally, a quantized plateau emerged at the neutrality point (V_t = 0) with G_2t = e²/h, consistent with helical edge conduction and matching the expected value for our geometry with N_L = N_R = 2. Geometry-dependent measurements (Extended Data Fig. 10c–e) further support the presence of helical transport, as altering the number of contacts along the edges between the source and drain changed the conductance, as expected from the above formula. In all configurations, the observed conductance at the neutrality point showed quantized plateaux matching theoretical predictions.

These results demonstrate helical edge states in proximity-screened graphene at magnetic fields more than an order of magnitude lower than previously required (more than 1 T) using a high-ε substrate³⁵. This highlights the potential of proximity-gated devices for accessing exotic quantum Hall phases at reduced magnetic fields by suppressing electron interactions.