The 3D helical flux ropes in VEST
Two essential magnetic field components, the poloidal and toroidal fields, are driven by external coils of VEST51, resulting in a 3D helical vacuum magnetic field configuration. Two flux ropes are discharged by negatively biasing arc plasma guns installed at the lower side of VEST, following the 3D field from each gun to the top plate of VEST38. A simple bias circuit is connected to the plasma guns in parallel with the VEST chamber wall, serving as ground. The vacuum poloidal and toroidal field strengths are set as 95 G and 120 G, respectively, giving the axial field strength at the gun location of 153 G. The total length of the followed field line and the total number of turns are calculated to be 11.3 m and 4.7 turns, respectively, based on the calculated vacuum field.
To provide a clearer view of the flux rope merging and reconnection experiment, a poloidal cross-section is shown in Extended Data Fig. 1b as a 2D view. The red lines are poloidal field lines induced by the flux rope currents, giving rise to an X-point between them with a co-helicity merging scheme in 3D, noted as a red cross. In this experimental scheme, other X-points may exist between the purple and yellow dots. However, the X-point shown in Extended Data Fig. 1b is the most favourable reconnection site, as the strength of the toroidal field (acting as the guide field in this reconnection experiment) is the lowest among the possible X-points.
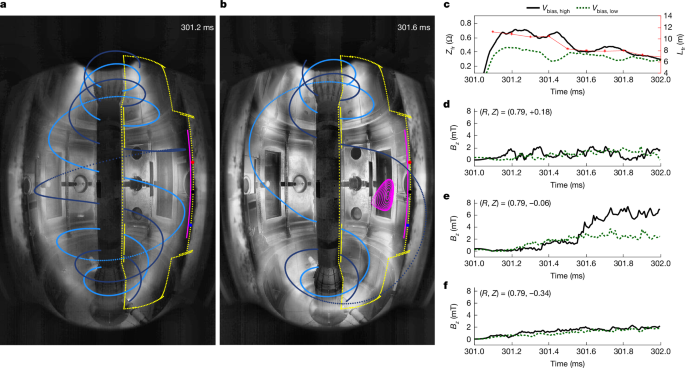
Extended Data Fig. 1c–e show the toroidal plasma, IP,toroidal, total flux rope current, Ifr,total, biasing voltage, Vbias, respectively, of two distinct flux rope discharges involving high (black lines) and low (green dotted lines) Vbias. The only difference in the two experimental conditions is Vbias, which sustains the flux rope discharge. An increase of IP,toroidal after 302 ms is evident only for the case of Vbias,high, compared with the case of Vbias,low. After 302 ms, the experiment and operation transition to a non-inductive current drive technique called electrostatic helicity injection36,37,38,43,52. Although the whole discharge time of experiments is 301–309 ms, the focus of this paper will be on 301–302 ms, for which we show MHD equilibrium changes by turbulent flux rope merging, which enable the eventual further increase in IP,toroidal (ref. 13). Further details on key experimental parameters can be found in Extended Data Table 1.
Limitations of MHD-driven merging
Although the flux ropes in our experiment exhibit 3D helical trajectories because of the background vacuum magnetic field, their stability can be well approximated by a 1D straight flux rope model. This simplification is justified by the boundary conditions—anchoring one end at the arc plasma gun and the other end at the top electrode—that constrain the current and magnetic field to follow primarily axial components. Consequently, the classical Kruskal–Shafranov threshold for ideal current-driven kink instability remains applicable. Assuming a flux rope radius of a = 3 cm, the Kruskal–Shafranov threshold for the ideal current-driven kink instability is calculated as 63 A. This interpretation is further supported by our previous experimental and phenomenological studies, which confirmed that the onset of kink instability in our system aligns well with a straight-line phenomenological model38.
In this experiment, the flux ropes are in a highly kink-unstable regime (Irope ≫ IKS), corresponding to an external kink state characterized by chaotic motion. In reality, this chaotic behaviour prevents the flux ropes from stably contacting each other, making merging through direct contact unfeasible under these conditions. Nevertheless, considering MHD forces alone, the high current of 0.75 kA per rope generates a strong mutual attractive force that could, in principle, lead to reconnection through MHD-driven motion10. However, this possibility is counteracted by a substantial restoring force resulting from the significant bending of the axial magnetic field of each rope11. The large initial separation of 30 cm requires a high curvature in the rope profiles, which gives rise to strong magnetic tension acting on each rope individually. This restoring force effectively suppresses their convergence, despite the mutual attraction. As a result, the displacement induced solely by MHD forces is insufficient to bring the flux ropes into contact within the Alfvén timescale. These results indicate that MHD forces alone are insufficient to induce reconnection under our experimental conditions.
The 3D field-following method
The 3D vacuum magnetic field path for each flux rope can be obtained by calculating the direction and strength of both toroidal and poloidal fields for given points. This calculation process is also called the field-following method53. The initial point for calculation is the location of arc plasma gun (Rinj, Zinj), as shown in Extended Data Fig. 1. Subsequent points are determined by adding the increments in both R and Z components, denoted as dR and dZ, respectively. Increments when the point moves dΦ in the toroidal direction can be obtained by using the following equations: \({\rm{d}}R=R\frac{{B}_{{\rm{R}}}}{{B}_{{\rm{T}}}}{\rm{d}}\varPhi \), \({\rm{d}}Z=R\frac{{B}_{Z}}{{B}_{{\rm{T}}}}{\rm{d}}\varPhi \). In this study, dΦ is set as 0.01745 radians (1°). Here BR and BZ are radial and vertical components of BP, respectively, thus satisfying \({B}_{{\rm{P}}}=\sqrt{{{B}_{{\rm{R}}}}^{2}+{{B}_{{\rm{Z}}}}^{2}}\). By denoting these 2D points every 0.01745 radians in 3D view, the final 3D field path can be achieved. The calculation stops when the calculated points meet the vessel wall. Moreover, the field-following length can be calculated as follows: \(L={\int }_{{\rm{a}}{\rm{l}}{\rm{o}}{\rm{n}}{\rm{g}}B\text{-}{\rm{f}}{\rm{i}}{\rm{e}}{\rm{l}}{\rm{d}}}\sqrt{{dR}^{2}+{dZ}^{2}}\). During the calculation, the effects of vacuum vessel eddy currents and non-uniform vertical fields are considered. The 3D path length at each time (Fig. 1c, red stars) is estimated using this field-following method, which considers not only the vacuum field but also the plasma in CFS.
MHD equilibrium reconstruction
An MHD equilibrium reconstruction code using the finite element method (FEM) has been developed to analyse the current density distribution and plasma equilibrium properties in VEST. The details can be found elsewhere54. In the present work, a total of 36 finite elements (6 × 6) are effectively distributed within the region R = (0.1, 0.6) m and Z = (−0.6, 0.6) m of the 2D poloidal cross-section (Extended Data Fig. 1b). As input data, 49 magnetic field pickup coils are used (27 on the inboard side and 22 on the outboard side). The current elements that reproduce the given field configuration are determined by minimizing a cost function, allowing for the evaluation of plasma shape and position parameters. The weighting factor is set to 10.
Ion Doppler spectroscopy system
The Ciii line (λ0 = 464.74 nm) is used for ion Doppler spectroscopy (IDS)55 in VEST because of its strong intensity and broad spatial distribution under VEST plasma conditions. The Doppler-shifted Ciii line was fitted with a Gaussian profile to obtain the ion velocity and temperature. Fitting errors are reported as 2σ (95% confidence interval). The IDS system consists of high-throughput collection optics, a spectrometer and a detector. In the collection optics, an objective lens (f/2, f = 35 mm) captures light from the plasma, and 10 fibres transmit this light to the junction box and spectrometer. The collection optics define the spatial coverage and resolution as R = 0.390–0.704 m and approximately 20 mm, respectively. The IDS diagnostic system features a wavelength coverage of 460–474 nm and a linear dispersion of 0.014 nm per pixel. An electron-multiplying charge-coupled device camera serves as the detector, which can operate with a temporal resolution of 1 kHz for 10-channel measurements. Owing to the setup of the IDS diagnostics, only the toroidal component was measured.
SXR measurement system
A 20-channel AXUV Si diode array was used in the VEST SXR measurement system and installed in one of the upper ports of VEST. The spatial resolution is 33 mm, and the sampling rate is captured at 125 MHz in the data acquisition system following pre-amplification. An aluminium filter of 0.1 μm was used to ensure transmission of energies 10 eV or greater. Further details can be found elsewhere56. Radially distributed 20 channels of SXR measurement system with a transmission filter of aluminium 0.1 μm were placed in the experiment to measure energetic particles of energies more than 10 eV.
Inductive voltage calculation from impedance of flux rope and fitting
The time evolution of inductive voltage for flux rope, VL, is calculated by fitting the following equation, \({V}_{{\rm{f}}{\rm{r}}}={V}_{{\rm{L}}}+{V}_{{\rm{R}}}={L}_{{\rm{f}}{\rm{r}}}\frac{{\rm{d}}{I}_{{\rm{f}}{\rm{r}}}}{{\rm{d}}t}+{I}_{{\rm{f}}{\rm{r}}}{R}_{{\rm{f}}{\rm{r}}}\) (ref. 57). The voltage sustaining the flux ropes can be decomposed into inductive and resistive components. The inductive component effectively represents the transient state of flux rope such as kink instability57, breaking and reconnection7, whereas the resistive component is related to more static characteristics of flux rope such as its length and area53. For the fitting, the measured Vbias, Ifr shown at Fig. 1d,e and numerically differentiated Ifr and dIfr/dt are used. Then 2D space of the Zfr and \(\frac{1}{{I}_{{\rm{f}}{\rm{r}}}}\frac{{\rm{d}}{I}_{{\rm{f}}{\rm{r}}}}{{\rm{d}}t}\) are plotted. In this paper, the time evolution of Lfr and Rfr are fitted every 0.2 μs. Finally, the time evolution of VL is obtained by multiplying fitted Lfr and measured dIfr/dt.
Measuring equipment and setup
Ifr is measured by a commercial Rogowski coil, CWTLF, from Power Electronic Measurements. The specification of the lab-made magnetic pickup coil and Rogowski coil measuring IP,toroidal can be found in ref. 54. For the voltage measurement, SVD10C of 3RLab is used, and the detailed power circuit can be found in ref. 38. IP,toroidal in Extended Data Fig. 1c was measured by a lab-made Rogowski coil connected to the VEST DAQ system at a sampling rate of 250 kS s−1. By contrast, key quantities analysed in this study—namely Irope, Vbias and BZ—were measured using a high-speed oscilloscope (MSO58 5-BW-2000, sampling rate 2.5 MS s−1) with short (about 2 m) shielded BNC cables. Irope was measured using a CWTLF/30 Rogowski coil with a sensitivity of 1.0 mV A−1 and a noise level of 15 mVp-p, corresponding to an uncertainty of ±5.3 A RMS (±0.71% for approximately 750 A signals). The Vbias was measured by an SVD10C differential probe with an accuracy of ±0.5%, yielding ±5 V uncertainty for 1,000 V. The propagated uncertainty in impedance Z = V/I was estimated using standard error propagation: \(\Delta Z/Z=\sqrt{{(\Delta V/V)}^{2}+{(\Delta I/I)}^{2}}\approx \sqrt{{(0.005)}^{2}+{(0.0071)}^{2}}\approx 0.87 \% \). Additional diagnostics, including ion temperature and toroidal flow from IDS and core emission profiles from SXR arrays, were obtained using dedicated setups in refs. 55,56, respectively.
Simulation setup
The open-source, fully relativistic particle-in-cell SMILEI code46 was used. The code normalization is based on a reference angular frequency ωr, which is set to be ωpe. All other reference quantities are derived from this reference frequency; for example, the reference length is c/ωpe.
The geometry of the fiducial run was Cartesian with a domain of (Lx, Ly, Lz) = (40, 40, 128)de divided into (80, 80, 256) cells, with 100 particles per cell. We also conducted runs with 2563 cells, but the reduced particles per cell due to computational resource limitations led to a larger numerical noise. Therefore, here the fiducial run is presented, but the two setups show qualitatively similar results. A reduced mass ratio of mi = 25me was used, and the Alfvén velocity was set to vA = 0.05c. A uniform background magnetic field was applied in the z direction. The plasma beta was 0.0564, the same for both species, which marginally satisfies the \(\frac{{m}_{{\rm{e}}}}{{m}_{{\rm{i}}}} < {\beta }_{{\rm{e}}} < 1\) condition for kinetic Alfvén wave instability. However, the electron temperature increases as the system progresses and so βe increases to a more intermediate value suitable for the instability. Additional simulations with mi = 100me were conducted, which show qualitatively similar merging behaviour as the fiducial runs. However, in this case, the increased Hall effect due to the large ion–electron scale separation may play a bigger part in the merging process, and so only the case with mi = 25me is presented here.
Two linear flux ropes were formed by injecting electrons at two localized points at z = 0 with a density profile \(n(x,y)\,=\) \({n}_{0}\exp [-\{{(x-{x}_{0})}^{2}+{(y-{y}_{k})}^{2}\}/{\sigma }^{2}]\), with x0 = 20de, yk=1 = 13de, yk=2 = 27de and σ = 1de, where de is the electron skin depth. The control case, corresponding to the Vbias,low condition in the experiment, was run with an injection velocity of vinj = 0.5c, whereas the test case, corresponding to the Vbias,high condition, had vinj = 0.9c. Note that these are not the eventual velocities of the electrons constituting the flux rope; the injected electrons form a double layer that induces secondary acceleration of the ambient electrons, which also reflect the impedance model of arc plasma gun operation40. The electron velocity in the flux rope in the control case satisfies vd < vA (vd ≃ 0.4vA), whereas for the test case, vd > vA (vd ≃ 2vA). The simulations were run for \(t=2,\,500{\omega }_{{\rm{ce}}}^{-1}\). For measurements that require increased temporal resolution, 7 × 7 × 7 = 343 numerical probes were located at regularly separated positions within the simulation domain with a sampling rate of fceΔt = 0.0327.
Beam-driven turbulence in the simulation
To verify that the increased drift velocity gives rise to an instability, a set of 2D simulations was conducted with parameters identical to the fiducial run except for a symmetry in the y direction, an increased particle-per-cell value of 1,000 and a single flux rope. The qualitative result is the same as that in the 3D case (Extended Data Fig. 2) The injected electrons mix with the thermal population and result in an increased effective temperature that renders the condition for kinetic Alfvén wave instability to be satisfied (Extended Data Fig. 3). For the test case, the injected electrons continuously form a bump-on tail distribution that keeps the instability going, whereas for the control case the system relaxes to a quasi-equilibrium. The obtained Fourier spectrum agrees well with kinetic Alfvén wave dispersion (Extended Data Fig. 4).
Turbulence-driven reconnection in the simulation
In the test case, the turbulence levels are much higher than in the control case (Extended Data Fig. 5a). This induces reconnection as can be seen in the increased of reconnected flux in Extended Data Fig. 5b. The magnetic energy density spectrum in Extended Data Fig. 5c is in qualitative agreement with the experiment (Fig. 3), namely, in that the fluctuations at kinetic scales are the strongest before merging and reduces thereafter, but still stronger than in the control case.
The role of turbulence in reconnection can also be directly demonstrated through the anomalous drag58 defined by \(D=-\frac{\langle \delta {n}_{{\rm{e}}}\delta {E}_{z}\rangle }{\langle {n}_{{\rm{e}}}\rangle }\), where the bracket denotes the average in the z direction and δ denotes fluctuating quantities, for example, δne = ne − ⟨ne⟩. This anomalous drag term contributes to the average Ez, thereby contributing to the reconnection electric field as well as particle acceleration and deceleration. This drag was found to be much higher for the test case, especially between the two flux ropes, the highest during reconnection, and smaller after merger (Extended Data Fig. 6).
Two alternative mechanisms that could also induce merging are the kink instability and attraction forces due to parallel currents. Taking the flux rope radius as 2.5de and length as 100de, the individual ropes are kink stable by an order of magnitude. The J × B force between the flux ropes was also found to be pinching only each flux rope (Extended Data Figs. 7 and 8).
Statistics
No statistical analyses were performed. Error bars in Fig. 2a,b represent 2σ fitting uncertainties from Gaussian fitting, corresponding to approximately 95% confidence intervals.