One-third of Sun-like stars are born with misaligned planet-forming disks

Protoplanetary disk inclinations

We assemble a catalogue of resolved protoplanetary disks by first referencing the list of resolved disks in the Catalog of Circumstellar Disks (https://www.circumstellardisks.org/), which identifies 227 disks around pre-main sequence stars as of its last update on 13 August 2021. We supplement these with entries from another recent compilation of ALMA-detected disks⁵¹, as well as resolved disks from individual studies compiled from the recent literature. This amounted to a sample of 690 unique systems. For this study, we isolate our sample to systems with well-determined inclinations (\(\sigma _i_\textdisk\) < 10°) derived from resolved submillimetre observations from ALMA (\(\sigma _i_\textdisk\) = 2.6°, on average). Our adopted measurements of i_disk therefore describe the orientation of dust in the outer disk at characteristic spatial scales of tens to hundreds of au. After filtering out disks that do not meet the uncertainty threshold, we are left with 172 systems. We then remove known binaries and stars with spectral types earlier than F6, yielding a sample of 94. Most stars belong to well-studied star-forming regions, primarily the Taurus-Auriga complex, the Lupus complex, and ρ Ophiuchi, with ages ranging from about 1 to 3 Myr (refs. ^{52,53,54,55,56}). For many disks, several independent inclination measurements have been made. For our analysis, we adopt the measurement of i_disk with the highest reported precision. We note that some disk inclinations are reported with asymmetric uncertainties. In these cases, we adopt the mean of the upper and lower limits.

Stellar properties

For each object in the initial sample of 94 single, low-mass, protoplanetary-disk-bearing stars, we compile vsini_*, P_rot and R_* measurements available in the literature. Rotation periods are either adopted from previous measurements or are newly determined using light curves from TESS or K2. After selecting for stars that satisfy the requirement that vsini_*, P_rot and R_* have been reliably measured (detailed below), we arrive at a final sample of 49 systems. A minimum uncertainty of 5% is imposed on all adopted stellar parameters if the reported values are smaller than this. Adopted values of T_eff, M_*, vsini_*, P_rot and R_* are given in Extended Data Table 1.

Projected rotation velocities

For each object in the sample, we compile published independent measurements of the stellar vsini_* that were obtained with high-resolution spectra and adopt the weighted mean. Because our measurements are drawn from a diverse array of sources, our adopted vsini_* could be subject to systematic effects related to data acquisition, processing and uncertainty estimation. To account for this, we impose a 5% lower limit on the precision of vsini_* to mitigate the possibility of a single measurement unfairly weighting the mean. Also, if an object has two or more measurements with no reported uncertainties, we combine them into a single average value and adopt the standard deviation as an estimate of the uncertainty. If only one vsini_* is reported without an uncertainty, it is excluded.

Rotation periods

We compiled stellar rotation periods in the literature drawn from independent datasets and adopt the weighted mean and uncertainty. To supplement these, we uniformly analyse TESS^57,58 and K2 (ref. ⁵⁹) light curves for targets in our compilation of resolved disks, avoiding the duplication of P_rot measurements from previous analyses of the same TESS and K2 datasets we consider here^{60,61,62,63,64,65,66,67}. We add new rotation periods for 43 objects.

We use the Python package Lightkurve⁶⁸ to download the TESS 2-min and K2 30-min cadence Pre-search Data Conditioning Simple Aperture Photometry (PDCSAP) light curves^69,70,71,72 and, for seven objects, we analyse the TESS light curves reduced with the MIT Quick-Look Pipeline⁵⁷. For K2 light curves in which instrumental systematics seem to be present in the PDCSAP data, we assess the K2 light curves reduced with either the EPIC Variability Extraction and Removal for Exoplanet Science Targets⁷³ pipeline (one object) or the K2 Systematics Correction⁷⁴ pipeline (two objects). Because of the potential for crowding in the field, we visually inspect each full-frame image to verify that there is no visibly apparent contamination from nearby stars.

We prepare the data products from each TESS sector or K2 campaign by removing any ‘NaNs’ from the data series and dividing the light curve by the median flux. Some objects were observed over several sectors or campaigns. If an object was observed over two or more consecutive TESS sectors, we stitch the data together to form one light curve. We do not merge light curves that are separated by one or more sectors because the spot evolution that occurs during long gaps in time may cause the rotation signature to no longer be coherent over the duration of the time series, making it difficult to properly assess the periodogram⁷⁵ and the phase curve. Next, we remove features unrelated to rotational variability from the data (that is, flares and other photometric outliers) by applying a high-pass Savitzky–Golay filter⁷⁶ and selecting only the points in the original dataset that fall within three standard deviations of the flattened time series. After detrending the data, we compute generalized Lomb–Scargle periodograms⁷⁷ of the prepared light curves with a sampling resolution of 0.01 days over a search window from 0.2 days to one-third of the total length of time in the light curve. We identify the stellar rotation period as that which corresponds to the maximum signal in the periodogram. The uncertainty on P_rot is estimated as the half-width of the peak profile in the power spectrum. If one object has more than one TESS or K2 light curve, each light curve is analysed separately and we adopt the weighted mean of the individual results.

Doppler imaging of young stars demonstrates that spots can exist at high and intermediate latitudes rather than at the equator^{78,79,80,81,82,83,84,85,86}. This can affect the measured rotation periods if the young stars in our sample experience differential rotation. Periodic signals detected in the light curves may not actually trace the equatorial rotation period used to compute the stellar inclination angle, which would bias the results towards higher values of i_*. We account for the effect of possible differential rotation of spots at unknown latitudes by inflating the uncertainties of the rotation periods with an error term σ_shear that represents half the maximum difference in rotation between the pole and the equator¹¹. This term relates the star’s absolute shear, ΔΩ (a metric to quantify differential rotation), and the equatorial rotation period, P_max, determined from the light curve:

We assume a Sun-like shear of ΔΩ = 0.07 rad day⁻¹ and add σ_shear in quadrature to the P_rot uncertainties from the periodogram analysis in our sample. Given that the exact spot distributions are unknown, we do not apply any explicit corrections to the measured period value.

Stellar radii

We adopt R_* estimates from the TESS Input Catalog⁸⁷ (TIC). Although the overall distribution of the TIC radii in our sample does not differ substantially from the weighted mean values of other radii found in the literature (Extended Data Fig. 1), adopting radii from the TIC ensures consistency across the sample. TIC radius estimates are determined by means of the Stefan–Boltzmann relation based on Gaia-determined distances, extinction-corrected G-band magnitudes and G-band bolometric corrections⁸⁸. Moreover, the accuracy of R_* in the TIC is well characterized; stellar radii in the catalogue are found to be typically within 7% of the values measured for the same stars with asteroseismology⁸⁹. We therefore inflate the uncertainties on R_* from the TIC by adding a 7% error term in quadrature with the nominal uncertainty¹¹. For most stars in the sample, there is no uncertainty reported with the TIC radius. For these objects, we assume a conservative uncertainty of 16%, which corresponds to the 95% quantile of the entire TIC radius uncertainty distribution. To this, we then add an extra 7% systematic error in quadrature.

The stellar radius and rotation period should always yield an equatorial rotation velocity (v_eq, in which v_eq = 2πR_*/P_rot) that is greater than or equal to vsini_*. Most of the sample follows this to within 2σ, with the exception of nine stars (2MASS J04202555+2700355, 2MASS J04360131+1726120, AA Tau, DoAr 25, FT Tau, IQ Tau, Sz 73, T Cha and WSB 52). This disagreement could be the result of potentially overestimated rotation periods, overestimated vsini_* or underestimated radii. The average P_rot and vsini_* of this subset (P_rot = 5.0 ± 2.7 days and vsini_* = 18.7 ± 9.3 km s⁻¹) compared with non-discrepant systems (P_rot = 4.8 ± 2.0 days and vsini_* = 16.6 ± 11.3 km s⁻¹) do not indicate that an overestimation of either parameter is the cause of the disagreement. However, the TIC radii of the stars in this subset are, on average, 36% lower than the mean of all non-TIC radii compiled for these same stars, whereas the rest of the objects in the sample that do not yield discrepant v_eq and vsini_* values are, on average, only 3% lower than the mean of their non-TIC counterparts. Some TIC radii may therefore be underestimated, leading to the disagreement in viable values of v_eq.

For the discrepant stars, we adopt radii from alternative sources, most of which originate from a separate catalogue of radius estimates⁹⁰ using spectra from the APOGEE⁹¹, GALAH⁹² and RAVE⁹³ surveys, validated with CHARA interferometry⁹⁴, Hubble Space Telescope flux standards⁹⁵ and asteroseismology⁹⁶, which we refer to as the Y23 catalogue. The Y23 catalogue has a characteristic accuracy within 5% of asteroseismology measurements⁹⁶. We thus add a conservative 5% systematic error term in quadrature to the uncertainties quoted in the Y23 catalogue. Four stars do not have a radius estimate from Y23 (2MASS J04202555+2700355, Sz 73, V1094 Sco and WSB 52), so we adopt the mean of the literature radii and estimate a conservative uncertainty equal to two times the standard deviation. After these adjustments to radii, the sample v_eq and vsini_* are consistent to within 2σ (Extended Data Fig. 2), the only exception being WSB 52, which is discrepant at the 2.4σ level. Five systems did not have reported TIC radii (2MASS J04334465+2615005, CIDA-7, Elias 2-24, MHO 6 and WSB 63), so for these systems, we also adopt the radius estimate from the Y23 catalogue, adding a 5% systematic error term in quadrature to the quoted uncertainties. All compiled values of T_eff, M_*, vsini_*, P_rot and R_* from the literature are provided in the Supplementary Methods.

Stellar inclination

With our adopted measurements of R_*, vsini_* and P_rot, we determine the stellar inclination i_* following a Bayesian probabilistic framework¹⁰, which properly accounts for the correlation between vsini_* and v_eq. In particular, we use the analytical expression for the posterior distribution of i_* (ref. ¹¹), which assumes an isotropic prior on i_* and considers uniform priors on vsini_*, R_* and P_rot (with a moderately precise measurement uncertainty of P_rot < 20%):

in which

and \(\sigma _P_\rmrot\), \(\sigma _v\sin i_* \) and \(\sigma _R_* \) are the uncertainties on the rotation period, projected rotational velocity and stellar radius, respectively. We note that the reported vsini_* measurements for four objects in our sample (2MASS J16083070-3828268, GW Lup, Sz 114 and Sz 130) are upper limits. For these cases, we use the analytical expression

in which l is the upper limit of vsini_*. The i_* posterior distributions are shown in the Supplementary Methods. For each star, we report the i_* MAP value and 68% highest density interval in Extended Data Table 2.

Star–disk minimum obliquity, Δi

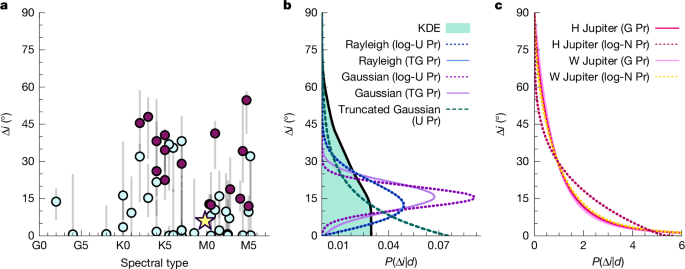
To determine Δi for each object, we randomly draw 10⁶ samples from the posterior distribution of i_* and the probability distribution of i_disk and compute the absolute difference between each sampled pair. Our adopted value of Δi is the distribution mode and our reported uncertainty range is the 68% highest density interval. Resulting Δi values and confidence ranges are provided in Extended Data Table 2 and Δi probability distributions are shown in the Supplementary Methods. Extended Data Fig. 3 shows Δi plotted as a function of system properties such as spectral type, M_*, T_eff, R_*, P_rot, vsini_*, i_disk and i_*. We compute the Pearson correlation coefficient, r, between Δi and each system property to test for correlated dependencies and identify no strong relationship with any parameter. Correlation coefficients in this test range from −0.04 to 0.37. These tests further yield high P-values, suggesting that any correlation indicated in the resulting r-values is statistically indistinguishable from the null hypothesis of no correlation. Correlation coefficients are shown in Extended Data Fig. 3. We note that the correlation coefficient for Δi with respect to i_* seems to be moderately correlated, with r = 0.37 and P = 0.01. However, these results do not take into account the uncertainties of the individual data points. When we repeat this test 100 times drawing Δi randomly from the individual probability distributions, the average Pearson r correlation coefficient is equal to 0.01, with an average P-value of 0.48. The moderate but notable correlation in i_* versus Δi that is initially apparent does not hold when taking into account the uncertainties in Δi. Repeating this procedure for all other system parameters yields similar results. We therefore identify no notable correlation in Δi with respect to spectral type, M_*, T_eff, R_*, P_rot, vsini_*, i_disk or i_*.

Because potential trends in Δi may not present only as a linear relationship, we conduct a second test to identify possible clustering of minimum obliquities at higher or lower values within subpopulations of dependent variables. Specifically, we separate the sample into two subgroups equal in size consisting of smaller or larger stellar parameters. We then determine the mean and standard deviation of each subgroup and compute the significance of the difference of the means. For every system parameter, the two subpopulations are consistent at a <1σ level. We therefore find no evidence that Δi clusters at low or high values for either subpopulation of sample parameters (Extended Data Fig. 3).

KDE of the Δi distribution

The KDE of the population-level Δi distribution is computed for 500 samples drawn from each individual Δi probability distribution in the sample (resulting in a total of 21,500 samples). We choose a kernel broadening parameter of 5.3°, which is the average deviation from the mean of the 68% confidence interval limits for each Δi distribution. Next, we use the uncertainties of i_disk, vsini_*, P_rot and R_* to generate a family of KDE reconstructions of the Δi distribution. For every object, we randomly sample 500 new values for each parameter, drawn from a normal distribution that reflects the adopted value and uncertainty of the parameter. From the samples, we generate 500 new Δi probability distributions for each object, which are then used to generate new KDEs following the same method to compute the nominal KDE. The diversity of the resulting family of KDE reconstructions is shown in Extended Data Fig. 4.

HBM of Δi

We estimate the underlying distribution of Δi with HBM using the open-source Python software ePop! (ref. ⁹⁷). Although the package was originally developed to model eccentricities, it can be generalized by mapping observations that span different ranges to a single domain from 0 to 1. ePop! uses an importance sampling methodology⁹⁸ and offers several choices for underlying parametric models, which have previously been used to characterize stellar obliquity distributions²⁸. In the context of HBM, the model parameters are hyperparameters with posterior distributions determined with the affine-invariant Markov chain Monte Carlo (MCMC) sampler emcee⁹⁹. Here we explore three population-level models to represent the underlying distribution in Δi. We choose these models because they are flexible and consist of just one or two free parameters, easing the interpretation of the results. The first underlying model we test is the Rayleigh distribution, \(\mathcalR(\Delta i|\nu )\), given by

The second is a Gaussian distribution, \(\mathcalN(\Delta i| \mu ,\sigma )\),

and the third is a truncated Gaussian, \(\mathcalT\,(\Delta i|\mu ,\sigma ,a,b)\),

where Φ is the cumulative density function of the standard normal distribution. We convert each object’s distribution in Δi (originally ranging from 0° to 90°) to a new, normalized variable Δi′ = Δi/90°, spanning the interval [a = 0, b = 1] to satisfy the generalized domain space in ePop!. The resulting posterior is then readily remapped to the original scale. Two hyperpriors are tested on the Rayleigh and Gaussian distributions to evaluate the degree to which our choice of priors affects the posteriors. We choose hyperpriors that have demonstrated the ability to produce families of distributions with sufficiently diverse morphologies to yield the most robust results⁵⁶. Our first hyperprior is a truncated Gaussian with μ′ = 0.69, σ′ = 1.0:

and our second choice of hyperprior draws from a log-uniform distribution ranging from 0.01 to 100:

We apply a uniform hyperprior:

for the truncated Gaussian underlying model, with μ ranging from –1,000 to 1,000 and σ from 0 to 1,000. Each MCMC run consists of 80 walkers for 6 × 10⁴ steps with a burn-in fraction of 50%. For both parametric models, we perform a visual inspection of the trace plots to ensure that the chains have properly converged. Each of the best-fit models of the underlying distribution of Δi yields similar results, indicating that the stellar obliquity distribution is broad (Extended Data Fig. 4). We provide the best-fit parameters and confidence ranges for the Rayleigh, Gaussian and truncated Gaussian models in Extended Data Table 3.

Characterization of systematics and biases

The distribution of MAP values of i_* shows that 14 out of 49 stars in our sample are equator-on with inclinations that are likely to be >80°. If the stellar orientation was randomly distributed–which is a reasonable assumption for isolated stars but may not be valid for this sample with resolved disks–the probability of i_* > 80° is \(\int _i_* =80^\circ ^i_* =90^\circ \sin i_* \rmdi_* =0.174\). This points to an expectation value of about 8 for a sample of 49 stars, suggesting that there may be a preference towards equator-on stars in the sample population above what would be expected by chance. Using binomial statistics, we can quantify the significance of this discrepancy by computing the probability of an event occurring that is at least as extreme as these measurements (k = 14 out of n = 49 systems). The probability of a success is P = 0.174 and so the probability of observing at least 14 stars out of 49 with i_* > 80° can be computed by taking 1 minus the probability of observing fewer than 14 stars with i_* > 80°: \(P(k\ge 14| p=0.174,\,n=49)=1-P(k < 14| p=0.174,\,n=49)\,=\,1-\)\(\sum _k=0^13\left(\genfrac0exnk\right)p^k(1-p)^(n-k)=0.054\). There is thus a probability of about 5% of there being at least 14 equator-on stars in our sample. The overrepresentation of high-inclination stars is mild, exceeding the expectation value by only 6.

Computational tools used

This research has made use of the VizieR (ref. ¹⁰⁰) catalogue access tool, CDS Strasbourg, France¹⁰¹ and the following open-source software: ePop! (ref. ⁹⁷), Lightkurve⁶⁸, Astropy¹⁰², NumPy¹⁰³, SciPy¹⁰⁴ and Matplotlib¹⁰⁵.