Remodelling of corticostriatal axonal boutons during motor learning

Animals

All experiments were performed in accordance with protocols approved by the Stanford University Animal Care and Use Committee, in accordance with the National Institutes of Health’s Guide for the Care and Use of Laboratory Animals. All mice were maintained with a 12 h:12 h light:dark cycle at a room temperature of 22 °C with humidity control (30–70%). Both male and female wild-type mice (C57BL/6 J, aged 7 weeks to 6 months) (Jackson Laboratory) were used.

Surgical procedures

We performed surgeries on mice under isoflurane anaesthesia (1.5% in 0.5 l min⁻¹ O₂). We used a combination of Cre and FLEX-GCaMP6s, FLEX-GCaMP8f or FLEX-eGFP viruses to achieve sparse labelling. To drive the expression of GCaMP6s or GCaMP8f in the motor cortex, we stereotaxically injected a mixture of AAV1-CAG-FLEX-GCaMP6s (100842-AAV1, 1:1) or AAV9-syn-FLEX-jGCaMP8f (162379-AAV9) and AAV5-hSyn-Cre (105553-AAV5, 1:200 diluted in saline) into the caudal forelimb area of the motor cortex (from bregma, anteroposterior (AP): 0.3 mm, mediolateral (ML): 1.5 mm; and from dura, dorsoventral (DV): −0.7 mm). Similarly, for structural imaging, we injected a mixture of AAV5-CAG-FLEX-eGFP (51502-AAV5, 1:1) and AAV5-hSyn-Cre (105553-AAV5, 1:1,000 diluted in saline). For expression of GCaMP6s in the thalamus, we injected a mixture of AAV1-CAG-FLEX- CaMP6s (100842-AAV1, 1:1) and AAV5-hSyn-Cre (105553-AAV5, 1:200 diluted in saline) into the PF (from bregma, AP: −2.3 mm, ML: 0.63 mm; and from dura, DV: −3.25 mm). A total volume of 100–300 nl was injected over 10 min, using a micro pump (WPI). To prevent viral backflow, the pipette was left in situ in the brain for 15 min post-injection before withdrawal. Upon completion of the procedure, the incision site was sutured, and the mice were returned to their home cage once they recovered from anaesthesia.

For the implantation of the chronic imaging window, 3–30 days after virus injection, we anaesthetized the mice with isoflurane (1.5% in 0.5 l min⁻¹ O₂). Following scalp removal, a titanium head plate was affixed firmly to the skull using super glue and dental cement (Lang Dental). A circular craniotomy with a diameter of approximately 2.4 mm was performed above the dorsal lateral striatum, centred at the coordinates (AP: 0.3 mm, ML: 4.0 mm). We aspirated the cortical tissue above the striatum using a 27-gauge needle at a 30° angle towards the surface of the corpus callosum^16,51. Subsequently, a cannula was inserted above DLS. The cannula consisted of a stainless-steel tube (~2.4 mm diameter, ~1.6 mm length) and a 2.4 mm round coverslip attached to one end of the tube using adhesive (Norland optical adhesive)^16,51. We then used Kwik-Sil and dental cement to fix the cannula and cover the exposed skull. Mice were returned to their home cage after they recovered from anaesthesia.

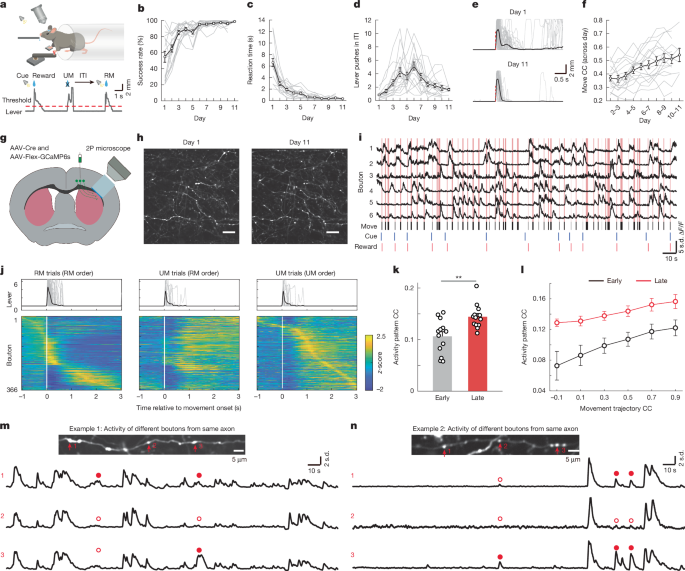
Two-photon imaging

In vivo imaging experiments were conducted using a commercial two-photon microscope (Bergamo II, Thorlabs), operated with ThorImage software. We used a 16×/0.8 NA objective (NIKON), covering a field of view (FOV) size ranged from 120 × 120 to 200 × 200 µm (1,024 × 1,024 pixels). A mode-locked tunable ultrafast laser provided 925 nm excitation for two-photon imaging (Insight X3 Spectra-physics). For calcium imaging, we imaged awake mice when they were performing the lever-pushing task. Imaging data were synchronized and recorded with a PCIe-6321 card (National Instrument) to capture image frame-out timing and behavioural events, encompassing cue, rewards, punishments, licking behaviour, and lever displacement. Time-lapse movies were acquired at an approximate frame rate of ~15 Hz. One to three days were imaged for the early stage and one to six days were imaged for the late stage. For imaging the same population of axons and boutons, same FOVs were imaged between early and late stage. The first 3 days were defined as the early stage, late stage was the days when mice learned the task (≥8 days). For example, one mouse was imaged on days 1–3 and days 9–11, then day 1–3 were defined as early stage, and days 9–11 were defined as the late stage. For corticostriatal axons using GCaMP6s, 13 mice were used in functional calcium imaging, including 8 mice imaged the same axons and boutons at the early and late stage, another 5 mice imaged different FOVs at the early and late stage of learning. For thalamostriatal axons using GCaMP6s, three mice were imaged at late stage of learning. Another three mice were imaged using GCaMP8f.

For structural imaging, mice were anaesthetized with 1–1.5% isoflurane and a heating pad was used to keep normothermia. Image stacks were acquired via real-time averaging of 20 frames, with a z-step of 1 μm to ensure precise axial resolution. For corticostriatal axons, 2–4 regions of interest (ROIs) were imaged per mouse, and these ROIs were repeatedly imaged every other day. Eight mice were used in structural imaging for the training group, and nine mice were used for the control group. For thalamostriatal axons, ROIs were imaged daily, three mice were used for the control group and four mice were used for the training group.

Cued lever-pushing task

The cued lever-pushing task was conducted as previously described¹⁶. In brief, mice were subjected to water restriction at 1 ml per day for three days. The lever-pushing task training started three days after water restriction and habituation. During habituation, mice were head-fixed and received water from the water tube. After starting the training, mice remained water restricted but received water during the training. Lever displacement was continuously monitored using a potentiometer, converting it into voltage signals, and recorded through a PCIe-6321 card (National Instrument). A custom LabVIEW program governed the training paradigm, precisely controlling cue presentation, reward delivery, punishment, and the determination of lever-pushing threshold crossing. Each trial was initiated with a 500 ms, 6-kHz pure tone as the cue. Mice received a water reward (approximately 8 μl) when they pushed the level surpassed the designated threshold (0.5 mm during the initial training on day 1, later increased to 1.5 mm for subsequent sessions) within the allocated task period. Failure to meet the threshold or absence of lever pushing during the task period resulted in the presentation of white noise. The ITI was either fixed at 4 s or randomly varied between 3 and 6 s. Lever pushing during the ITI incurred an additional timeout equivalent to the ITI duration for that specific trial. The task period was 30 s during the first session and then reduced to 10 s for subsequent sessions. The ITI was defined as the time from the end of the last trial (reward or punishment) to the start of the next trial (cue) and does not include the allocated task period. In a subset of mice, we randomly added reward delay trials and reward omission trials on one imaging day while imaging the same population of boutons. In reward delay trials, the reward was not delivered immediately after the lever exceeded the threshold, but was delivered 1 s after the lever exceeded the threshold. In reward omission trials, the reward was not delivered even when lever exceeded the threshold. In a further subset of mice, we included cue-only or punishment-only trials after mouse finished performing the lever-pushing task. A total of 37 mice were trained, mice learned the task within 3 weeks, including 19 mice for calcium imaging and, 12 mice for structural imaging, and 6 mice used for behaviour training.

Movement behaviour analysis

To identify movement bouts, we first determined a threshold to separate the resting and movement period. Movement bouts separated by less than 500 ms were considered continuous and were combined together^11,16. The start time was identified as the point where the lever position crossed a threshold that exceeded the resting period, while the end time was determined by detecting the moment when the lever position fell below the threshold^11,16. To ensure the integrity of the baseline before each movement, we adopted a specific criterion. If there were any other movements occurring within a 3-s window before a particular movement, the latter was excluded from further analysis. This exclusion step was implemented to guarantee the cleanliness and reliability of the baseline period, thus enhancing the accuracy of subsequent analyses. RM was defined as lever pushes that exceeded the threshold during the task period, while UM was those lever pushes that failed to exceed the threshold during the task period, or lever pushes during ITI.

Activity pattern correlation and its relationship to movement trajectory correlation

The activity pattern correlation was calculated based on single trial pairs using population bouton activity for each mouse. Therefore, the activity of all responsive boutons in an imaging FOV were concatenated for each trial in the same order and the trial-to-trial correlation of this population activity vector was calculated. Activity pattern correlation and movement trajectory correlation were calculated for each trial pair using MATLAB function corrcoef. For all trial pairs in one day, we used bins −0.2 to 0, 0 to 0.2, 0.2 to 0.4, 0.4 to 0.6, 0.6 to 0.8 and 0.8 to 1 to average all data points based on movement trajectory correlations. Then the activity pattern correlation was plotted against the movement trajectory correlation for each mouse.

Fraction of activated ensemble difference and its relationship to movement trajectory correlation

Percentage of activated ensemble difference was calculated based on each pair of trials, if a is the number of activated bouton ensemble in trial 1, and b is the number of activated bouton ensemble in trial 2, then the fraction of activated ensemble difference for this trial pair is defined as \(\frac0.5\times (a+b)\), in which |a − b| was the difference in the number of activated ensembles, and \(0.5\times (a+b)\) was the average number of activated ensembles for the trial pair. Then we calculated correlation of the movement trajectory for each trial pair using MATLAB function corrcoef. For all trial pairs in one day, we used bins −0.2 to 0, 0 to 0.2, 0.2 to 0.4, 0.4 to 0.6, 0.6 to 0.8 and 0.8 to 1 to average all data points based on movement trajectory correlations. Then the percentage of activated ensemble difference was plotted against the movement trajectory correlation for each mouse.

Image processing and analysis

For Ca²⁺ image analysis, lateral motion artifacts were corrected using the ImageJ plugin Turboreg⁵² or the efficient subpixel image registration algorithm⁵³. ROIs for axons, axonal shafts and boutons in FOV were manually drawn using Adobe Photoshop session-by-session. For the same FOV imaged both in early and late stages, only boutons with clear bouton morphology that could be identified in all sessions by visual inspection were selected and further analysed. On average 44.3 ± 7.9 (ranging from 10–85) axon segments were analysed per mouse with an average of 10.66 ± 1.66 boutons (early) and 11.2 ± 1.9 boutons (late) per axon segment for M1-DLS projections and 26 ± 16.5 (ranging from 16–45) axon segments per mouse with an average of 6.47 ± 0.88 boutons (late) for PF-DLS projections.

To extract the calcium signals for each axon or bouton, we averaged the fluorescence intensity of all labelled pixels to obtain the raw fluorescence trace. To calculate F₀, we utilized a 30-s sliding window, where the 30th percentile of raw fluorescence within the window was designated as F₀. ΔF/F was computed as (F − F₀)/F₀ for each individual axon and bouton⁵⁴. For data presentation, a z-score of this ΔF/F trace was further calculated.

To confirm that the observed signal was not caused by motion artifacts, we plotted the fluorescence signal of inactive boutons and found no detectable activity across many movement trials (Extended Data Fig. 15).

For structural imaging, individual boutons were identified as swellings along thinner axon shafts, and were manually identified, marked, and tracked across multiple imaging sessions using the custom written script (MATLAB). Only high-quality images displaying sparsely labelled axons, with distinct axon and bouton structures, were selected for subsequent quantification. Analysis of bouton dynamics, including formation and elimination, was performed by comparing boutons between two adjacent imaging sessions. Boutons were classified as ‘persistent’ if they were present in both images, determined through their positions relative to nearby boutons within the same axon. An eliminated bouton was the one that appeared in the initial image but not the second image. A newly formed bouton was the one that was absent in the initial image and then appeared in the second image. The bouton survival rate was calculated as the percentage of boutons formed during day 4 of training that remained present in subsequent training sessions (days 6, 8 and 10).

Identification and classification of RM and UM axon and bouton

The activities of individual axons or boutons in both RM trials and UM trials were aligned to the movement onset, spanning a time window from 1 s before movement initiation (served as the baseline) to 3 s after the movement onset. Subsequently, we calculated the average activity across all trials within this aligned time window. To identify responsive boutons, we examined the peak value of each bouton within the time window (−0.2 to 3 s relative to the movement onset). Boutons were considered responsive if the difference between the peak fluorescence value and the 5th percentile of the averaged activity exceeded 90% of the s.d. For the identification of responsive axons, we plotted histograms of all peak values in RM and UM trials for each mouse. Utilizing a bin size of 0.1× s.d., the peak bin values were determined for both RM and UM distributions, and the threshold was established as the mean of the corresponding peak positions in RM and UM. If the calculated threshold, based on the histogram distribution, exceeded 1× s.d., the final threshold was set at 1× s.d. Responsive axons were identified if the difference surpassed the threshold by comparing each axon’s peak value to the 5th percentile of the averaged activity. Subsequently, axons or boutons were categorized based on their responsiveness in RM and UM trials. Those identified as responsive exclusively in RM trials were classified as RM-only axons or boutons, while those responsive only in UM trials were categorized as UM-only axons or boutons. Axons or boutons showing responsiveness in both RM and UM trials were designated as RM–UM both axons and boutons. To simplify, we combined the RM-only and RM–UM both categories, grouping them as RM, RM-responsive or RM-related axons and boutons. To calculate the delay reward related boutons, we first calculated the activity peak time for each bouton during RM and delay reward trials. If the activity peak time of a bouton was postponed more than 0.93 s, we categorized this bouton as delay reward modulated bouton. Those delay reward modulated boutons were considered to be modulated by reward, rather than movement. To analyse the activity of those reward modulated boutons in reward omission trials, we averaged the calcium activity over a window of 1.67 s to 2.33 s relative to movement onset for delay reward trials and 0.67 s to 1.33 s relative to movement onset for omission trials.

Ca²⁺ event detection and identification of same or unique peaks

To detect Ca²⁺ events, we employed the Matlab findpeaks function with the following criterion⁵⁵: z-scored ΔF/F₀ exceeding 1× s.d. To compare events between pairs of boutons, we considered any events occurring within 670 ms of each other as ‘matched’ and defined them as the same peak⁵⁶, while those peaks that cannot find matched peaks were defined as unique peaks. If the same peaks or unique peaks occurred during a time window 330 ms before and 670 ms after the onset of RM or UM, those peaks were classified as RM or UM-related same or unique peaks, respectively. To calculate the same or unique peak fraction, we divided the number of same peaks with total peaks based on each bouton pair or bouton–shaft pair, and averaged the results over all boutons within one axon, then averaged over all axons in one mouse.

Principal components analysis

We used PCA to project each trial into a lower-dimensional space to discern the low-dimensional embedding of individual boutons during RM and UM trials. Initially, the activity of each bouton was averaged across all RM or UM trials, and the averaged activities were then concatenated for each bouton. We recorded the results in a data matrix where each column represented the concatenated trial-averaged RM and UM activity of one bouton. The size of the matrix was 2M × N, with M denoting the number of timepoints per RM or UM trial (ranging from –1 to 3 s relative to movement onset), and N representing the number of boutons. Subsequently, PCA was conducted across the timepoints of concatenated RM and UM trials, capturing the first three principal components to represent the RM and UM trials in a visually informative 3D principal component space. Each bouton was depicted as a distinct dot within this space, facilitating clear visualization and discrimination of the bouton responses during both RM and UM trials. We used the Matlab pca function to perform dimension reduction.

PCA trajectory and calculation of selectivity index

PCA was conducted using the Matlab pca function on each continuous imaged segment (4,000 frames by n boutons, frame rate: 15 Hz), utilizing the first three principal components to represent the ensemble activity of boutons. Then we aligned the first three principal components from 1 s before to 3 s after each RM and UM onset to generate single RM or UM neural trajectories in the PCA space. We used activity trajectory selectivity index to measure the selectivity of bouton activity towards RM or UM, a method modified from a previously published paper⁵⁷. The activity trajectory selectivity index for an RM trial was defined as (d_{to mean UM trajectory} – d_{to mean RM trajectory})/(d_{to mean RM trajectory} + d_{to mean UM trajectory}), where d_{to mean UM trajectory} is the Euclidean distance between the single RM trial trajectory and the mean UM (RM) trajectory, which was computed frame by frame. The mean RM and UM trajectories were the averages of all RM and UM trajectories, respectively. For example, if the first three principal components of the first frame of a RM trial are \((a,b,c)\), while the first three principal components of the first frame of the mean UM trial are \((x,y,z)\), then the d_{to mean UM trajectory} is \(\sqrt(a-x)^2+(b-y)^2+(c-z)^2\). Similarly, the activity trajectory selectivity index for a UM trial was defined based on distances as (d_{to mean RM trajectory} – d_{to mean UM trajectory})/(d_{to mean RM trajectory} + d_{to mean UM trajectory}). The trajectory selectivity index essentially measures how closely individual trajectories match the mean trajectories of their respective trial type versus the opposite type. For example, for an RM trial, an index score of 1 means the single trial trajectory was at the same point in PCA space as the mean RM trajectory, and an index score of −1 means the single trial trajectory was at the same point in state space as the mean UM trajectory.

Axon–axon and bouton–shaft correlation analysis

Axon–axon and bouton–shaft correlation were calculated using MATLAB function corrcoef. Axon–axon correlations (in Extended Data Fig. 12) and bouton–shaft correlation (in Extended Data Fig. 7b) were calculated using data from each continuous imaged segment (4,000 frames by n boutons, frame rate: 15 Hz), then averaged over sessions on each day. For the bouton–shaft correlations of small and large peaks (in Extended Data Fig. 7d), we first identified peaks, then used data from 20 frames (5 frames before the peak position and 15 frames after peak position) to calculate the peak correlation, then averaged over all peaks in one session, then averaged over all sessions on each day. Small and large peaks were defined as peaks with an s.d. of 1–2 and 8.5–9.5, respectively.

Nearest neighbour analysis

For each bouton, we calculated its Euclidean distances to all other boutons within the same axon, then the bouton with smallest distance were termed its nearest neighbour, and the distance was termed NND. To calculate NND distribution of the shuffled group, we randomly shuffled the bouton positions 1,000 times using MATLAB function randperm.

Statistics

Significance testing was performed using the Wilcoxon rank sum test, Pearson correlation coefficient, one-way ANOVA, two-way ANOVA, paired t-test, and Kolmogorov–Smirnov test using Matlab and Microsoft Excel. Two-sided statistical tests were conducted, and data are presented as mean ± s.e.m., with all statistical tests, statistical significance values, and sample sizes described in the figure legends. *P < 0.05, **P < 0.01, ***P < 0.001; NS, not significant. All source data are included in the source data table. Sample size was first estimated on the basis of our lab’s previous established protocols and previous publications. After we had an estimate of the data variance and distribution, power analysis was used to confirm that our estimated sample sizes were sufficient. We performed power analyses using the formula N = (ZS/E)², where Z is the statistical significance level, S is the standard deviation and E is the margin of error. Mice were randomly assigned to control and training groups. All experiments were repeated in a minimum of three cohorts. All attempts at replication were successful. Experimenters were not blinded to experimental conditions during data collection since all mice had to progress through early and late phases of learning, which are the main condition used for comparison. Experimenters were blinded to experimental conditions during data analysis.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.