Evidence of Coulomb liquid phase in few-electron droplets

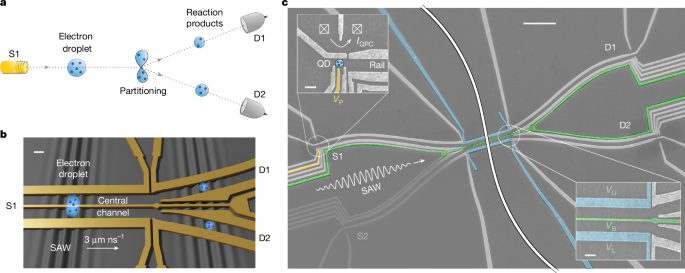
Device description

The device is fabricated in a Si-doped GaAs/AlGaAs heterostructure grown by molecular-beam epitaxy. The 2DEG resides 110 nm below the surface, with electron density 2.8 × 10¹¹ cm⁻² and mobility 9 × 10⁵ cm² V⁻¹ s⁻¹. Metallic gates (Ti, 3 nm; Au, 14 nm) are deposited on the surface of the semiconductor using electron-beam lithography. All measurements are performed at a temperature of about 20 mK in a ³He/⁴He dilution refrigerator. The sample and measurement scheme are the same as in ref. ¹⁸. A set of negative gate voltages is applied to the surface gates to deplete the 2DEG underneath and create the nanostructures, including four QDs, four QPCs and two guiding rails, which are fully depleted. These rails connect the source QDs to the detector QDs and merge in the centre to form a single 40-μm-long channel, equipped with a narrow barrier gate in the middle to tune the shape of the confining potential from a single well to a double well.

SAW generation

The SAW is generated using a double-finger IDT deposited on the surface and placed at a distance of 1.5 mm from the device. The metallic fingers are fabricated using electron-beam lithography and thin-film evaporation (Ti, 3 nm; Al, 27 nm) on the heterostructure. The IDT consists of 111 cells with a periodicity of 1 μm and a resonance frequency of 2.86 GHz at low temperature. The aperture of the transducer is 50 μm. To perform electron transport by SAW, a radiofrequency signal is applied on the IDT at its resonance frequency for a duration of 60 ns. To have a strong SAW confinement potential, the signal is amplified to 28 dB using a high-power amplifier before being injected into a coaxial line of the cryostat through a series of attenuators. The velocity of the SAW is 2,860 m s⁻¹.

Electron transfer

Each single-shot experiment corresponds to the transfer of one or a few electrons from the source QDs to the detector QDs using the SAW as the transport carrier. To prepare a given number N of electrons in a source QD, we use a sequence of fast voltage pulses to the channel gate and reservoir gate controlling the tunnel barriers of the QD. This sequence consists of three steps: initializing the QD, loading the electrons into the QD and preparing the QD for electron transfer. To initialize the source QD, electrons previously present in the QD are removed. Then, a given number of electrons are loaded into the QD by accessing a particular loading position in the charge-stability diagram of the QD. Finally, these electrons are trapped within the QD by switching to a holding configuration, from which they will be taken away by the SAW. At the same time, the two detector QDs are set in a configuration for which the electrons transported by the SAW will be captured with high fidelity. For more details, see Supplementary Note 1. By sensing the QPC currents of both the source and detector QDs with single-electron resolution and comparing their values before and after the electrons are transferred by the SAW, the precise number of electrons transferred to each detector can be determined. When calculating the partitioning probability, the very few events that do not conserve the total number of electrons are excluded by a post-selection routine.

In our experiment, the electrons are deterministically loaded into specific locations within the SAW train. The plunger gate of the QD is used to trigger the sending of the electrons into a precise minimum of the periodic SAW potential with a 30 ps resolution. This precise control allows for the formation of an electron droplet containing up to five electrons, using the two source QDs of the device. To synchronize the two trigger pulses with the radiofrequency signal generating the SAW, we use two arbitrary waveform generators combined with a synchronization module. The outputs of the arbitrary waveform generators are connected to the plunger gates by means of high-bandwidth bias tees for voltage pulsing and dc biasing.

Electron partitioning

The electron droplet is partitioned at the Y-junction located at the end of the central channel, after a flight time of 14 ns. By applying a voltage detuning Δ = V_U − V_L, in which V_U and V_L are the voltages applied to the side gates of the central channel, we can control the partitioning ratio between the two detectors D1 and D2. For all partitioning experiments reported here, the barrier gate voltage is set to V_B = −1.25 V to have a single central channel with a weak double-well potential profile. Careful analysis of the double-well potential and the electron number equilibration in the central channel is described in Supplementary Notes 2 and 3.

Statistical uncertainty

The error in estimating the probability p_n from the counting statistics is dictated by the distribution of independent Bernoulli trials. The corresponding likelihood function of measuring exactly N_n outcomes of n particles in detector D1 out of N_rep repetitions is \(\left(\beginarraycN_\rmrep\\ N_n\endarray\right)p_n^N_n\)\((1-p_n)^N_\rmrep-N_n\). We use the mean N_n/N_rep as the statistical estimate for p_n. The boundaries of the corresponding confidence interval (CI) at confidence level 1 − c = 95% are determined from the likelihood function by inverting a one-tailed binomial test at significance level c/2, for the lower bound and the upper bound separately. At the extreme count N_n = 0 (N_n = N_rep), the lower (upper) boundary is set to 0 (1) and the other boundary is computed at significance level c. These CIs of probability measurements are used in the Ising model parameter estimation. For 0.06 < p_n < 0.94 in our measurements with N_rep = 3,000, the CIs are almost symmetric and approximately given by \(\pm 1.96\sqrtp_n(1-p_n)/N_\rmrep\). Because the maximum width of the CI is about 0.036 (at p_n = 0.5), a value smaller than the size of the data points, we did not represent the error bars on the graphs of probabilities.

Symmetrized multivariate cumulants

In our experiment, the observable is the number n of electrons measured at detector D1, which can be expressed as a sum of binary variables T_j. From \(n=\sum _j=1^NT_j\) and \(T_j^2=T_j\), we derive the general relation

between the probabilities p_n = P_(N−n,n) of the full counting statistics (FCS)²¹ and the kth-order symmetrized multivariate moments m_k defined as averages of all permutations of k distinct variables,

in which \(\left(\beginarraycN\\ k\endarray\right)=N!/[k!(N-k)!]\) is the binomial coefficient. The corresponding symmetrized multivariate cumulants

are, in general, not uniquely determined by FCS probabilities and their calculation requires further information (such as symmetry constraints or a microscopic model).

For statistically equivalent particles (that is, full permutational symmetry of the multivariate probability distribution), all terms in equations (3) and (4) are equal, and the moments m_k can be related to cumulants κ_k through standard univariate relations⁵¹, \(\textln(1+\sum _k=1^\infty m_kz^k/k!)=\sum _k=1^\infty \kappa _kz^k/k!\). Using an explicit formula in terms of Bell polynomials⁵², we can write

See Supplementary Note 5 for the derivation of equation (2) and explicit formulas for κ_k for k = 1–5. An example of correlated partitioning, in which equation (5) is not valid and the general combinatorial expressions for multivariate cumulants^39,53 need to be used, is shown in Fig. 2e and described in detail in Supplementary Note 6.

There is an important distinction between our method for extracting interaction signatures and the approach of so-called factorial cumulants considered in the context of electron transport³² and particle physics⁵⁴. The multivariate moments defined by equation (3) can be written m_k = ⟨(n)_k⟩/(N)_k, in which (x)_k = x(x − 1) ×…× (x − k + 1) is the falling factorial and ⟨(n)_k⟩ is known as the factorial moment of FCS³². The k-dependent denominator (N)_k in this expression for m_k makes the κ_k distinct from the factorial cumulants; see further discussion in Supplementary Note 5.

Ising model on a complete graph

The Ising model on a complete graph is exactly solvable⁵⁵ and, hence, equilibrium fluctuations at any freeze-out quench temperature T can be computed for any N. The Ising Hamiltonian of equation (1) can be expressed as a quadratic form of the observable \(n=\sum _j=1^NT_j\),

The corresponding exact counting statistics in a canonical ensemble is p_n = c_n/Z with the partition function \(Z=\sum _n=0^Nc_n\) and the statistical weights

in which β = 1/k_BT. Together with equations (2) and (5), this gives a way to calculate the exact multivariate cumulants κ_k of all orders k ≤ N at any N.

To make the connection with the thermodynamic phase diagram in terms of μ and T in the large-N limit, explicit analytic expressions are obtained following ref. ⁵⁵. We apply the lowest-order Stirling’s formula \(m!\approx m^me^-m\sqrt2\pi m\) to the factorials in the binomial coefficient \(\left(\beginarraycN\\ n\endarray\right)\) in equation (7) and perform expansion of ln(c_n) near its maximum n ≈ ⟨n⟩ up to quadratic order. This results in a Gaussian approximation to p_n of the form

in which β′ = [4κ₁(1 − κ₁)k_BT_N]⁻¹ and k_BT_N = UN/2 is the zero-field Néel temperature for the antiferromagnetic crossover. The relation between the effective magnetic field μ and the effective magnetization κ₁ = ⟨n⟩/N in the large-N limit is given by the transcendental equation⁵⁶

which has only one solution for the antiferromagnetic sign of the coupling (U > 0).

To quantify the antiferromagnetic correlations in the thermodynamic limit, we choose the pair correlation function ⟪T₁T₂⟫ = κ₂ as the order parameter. It is obtained from the identity ⟨n²⟩ − ⟨n⟩² = Nκ₁(1 − κ₁) + N(N − 1)κ₂ in the large-N limit. Treating n as a continuous variable and using the Gaussian approximation of equation (8), this gives the leading-order behaviour of κ₂ at a fixed T/T_N and N → ∞,

A numerical solution to equation (9) together with equation (10) is used for the phase diagram in Fig. 4b.

As there is no lattice on a full graph favouring a particular pattern of staggered magnetization, the antiferromagnetic transition here is not a second-order phase transition but a crossover. The corresponding change in free energy has a weaker divergence (logN) in the thermodynamic limit than at the ferromagnetic transition. The corresponding singular part⁴⁶ of the free energy change between T = ∞ and T → 0⁺ is βΔF_U>0 = (1/2)ln(1 + T_N/T).

On the ferromagnetic side (U < 0), we note that κ₂N diverges when the temperature T approaches the Curie temperature T_C = −T_N > 0 as κ₂N ∝ (T − T_C)⁻¹ for \(T\to T_\rmC^+\). At T ≤ T_C, the Gaussian approximation of equation (8) breaks down and strong ferromagnetic order sets in. This corresponds to the droplet scattering at the Y-junction as a whole (without partitioning), with probability κ₁ to go to detector D1 and with κ₂ = κ₁(1 − κ₁) > 0 in the large-N limit. For a large but finite droplet, there is no symmetry breaking, hence κ_k>1 = O(1), unlike O(N^−k+1) in the antiferromagnetic case.

Universal scaling of partitioning cumulants

The interaction-dominated partitioning of a large droplet at U > 0 is described by the antiferromagnetic phase of the effective Ising model with T/T_N → 0 and N → ∞. The Boltzmann factor in equation (7) suppresses the fluctuations of n around ⟨n⟩ = κ₁N and caps the large-N asymptotics of univariate cumulants from ⟪n^k⟫ = O(N) (Gaussian limit of binomial distribution) to ⟪n^k⟫ = O(1). From the latter condition (which is independent of the specifics of the Ising model), we derive the asymptotics κ_k = G_k(κ₁)N^−k+1 + O(N^−k) for k ≥ 2, in which the prefactor

is universal and given by the ultraspherical (Gegenbauer) polynomials \(C_k^(a)\) of degree k and parameter a = −1/2. The first polynomials up to k = 5 are plotted in Fig. 3a, to show the universal strong-correlation asymptotics of the scaled cumulants κ_kN^k−1. Note that G₂ = −κ₁(1 − κ₁) is also the zero-temperature limit of equation (10).

The polynomials G_k(κ₁) have exactly k − 2 zeros for 0 < κ₁ < 1, which explains the observed oscillation pattern and provides an exact specific example of oscillations in high-order cumulants³¹. We note that a similar generic N^−k+1 scaling has been discussed for cumulants of initial density perturbations in heavy-ion collisions⁵⁷, in which it arises for different reasons (dominance of autocorrelations in the independent point-sources model).

In contrast to antiferromagnetic correlations decaying with N as κ_k ∝ N^−k+1, the fluctuations in the ferromagnetic case are between n = 0 and n = N only, hence κ_k = O(1), and the limiting form for the unpartitioned scattering (T/T_C → 0 in the Ising model) is the polynomial \(\kappa _k=-\rmLi_1-k\left(\frac\kappa _1\kappa _1-1\right)\), in which Li is the polylogarithm.

Coulomb liquid simulations

We model a finite droplet of Coulomb plasma in 2D using a confining single-electron potential V_1e and an unscreened Coulomb potential⁴⁷, which results in the total potential

in which r_i = (x_i, y_i) is the in-plane coordinate of the ith electron and ϵ_r = 12.1 is the relative dielectric permittivity in GaAs. The equilibrium distribution of electron coordinates is determined by a classical canonical ensemble at an effective temperature T. We sample electron positions r_i using a random walk Metropolis Monte Carlo algorithm designed to sample the canonical distribution. The convergence of the corresponding Markov chain is controlled by the Kolmogorov–Smirnov test⁵⁸. For each set of parameters, a statistics of positions is collected with the estimated effective sample size ranging from 10³ to 10⁵ depending on parameters. The statistics of positions is translated to partitioning statistics of a sudden quench using binary variables T_i = Θ(y_i), in which Θ is the Heaviside step function. This corresponds to an observable n = T₁ +…+ T_N counting the number of particles in the y > 0 half-plane.

The confining electrostatic potential of our experiment can be approximated as a double-well quartic-parabolic 2D potential

in which V_b is the height of the central barrier, y₀ is the distance between the two minima, μ_q is the transverse energy detuning proportional to the side-gates voltage difference Δ − Δ₀ (which controls the partitioning of the droplet) and ω_x is the oscillation frequency in the longitudinal direction, resulting from the confinement potential of the SAW.

The barrier height V_b = 27.5 meV and the distance between minima y₀ = 220 nm are estimated from an electrostatic simulation of the gate-controlled potential as explained in Supplementary Note 2. The transverse oscillation frequency in the two potential minima is then calculated as \(\omega _y=\sqrt32V_\rmb/(my_^2)=7.0\,\rmTHz\) using the effective mass m = 0.067m_e for electrons in GaAs. The longitudinal oscillation frequency in the SAW potential is estimated from the peak-to-peak amplitude A_SAW = 42 meV and wavelength λ_SAW = 1 μm, using the relation ω_x = (π/λ_SAW)(2A_SAW/m)^1/2 = 1.5 THz (see Supplementary Note 4 in ref. ¹⁸). The aspect ratio of the 2D confinement is thus ω_x/ω_y = 0.21.

The potential being entirely determined, the effective electron temperature T is the only free parameter to be chosen for good agreement with the experimental data, as shown by the solid lines in Fig. 3b–e using T = 25 K. This value is also consistent with the one extracted from the barrier-height dependence of the thermally activated hopping rate between the two wells of the quartic potential, as estimated in Supplementary Note 2.