Warming accelerates global drought severity

Drought index

The SPEI³¹ is a widely utilized drought assessment tool that incorporates both AED and precipitation to evaluate drought severity across different timescales. SPEI values are computed by subtracting AED from precipitation. These differences are standardized using a log-logistic probability distribution to ensure consistency across regions, seasons and timescales. This distribution model involves three parameters (α, β and γ), which are estimated using the L-moment procedure. The SPEI indices were calculated using the entire 1981–2022 period as a baseline, ensuring that the full range of variability in the input data is captured. Unlike other drought indices, the SPEI does not require a predefined baseline or calibration period, as it standardizes the data directly from the input time series, ensuring consistency across datasets and timescales. The SPEI values provide categories for wet and dry events (Extended Data Table 1).

Using SPEI, we developed four high-resolution SPEI indices using a combination of two precipitation datasets and two potential evapotranspiration (that is, AED) datasets. The precipitation datasets used were the MSWEP⁴¹ and CHIRPS⁴⁰ precipitation and the AED datasets were GLEAM⁴² and hPET⁴³. The resulting four indices: MSWEP_GLEAM, MSWEP_hPET, CHIRPS_GLEAM and CHIRPS_hPET, were developed at a spatial resolution of 0.05° for the period 1981–2022. The 0.1°-resolution datasets were first interpolated to match the resolution of CHIRPS using bilinear interpolation. In addition, we developed an ensemble mean (HRSPEI) based on all four datasets. For latitudes above 50° N, the mean is derived from MSWEP_GLEAM and MSWEP_hPET, as CHIRPS data are available only up to ±50° latitude. AED and AED variability in high-latitude areas >50° N are generally small, and changes in AED, even at high percentages, result in low absolute magnitudes, making SPEI less sensitive to AED in these regions³².

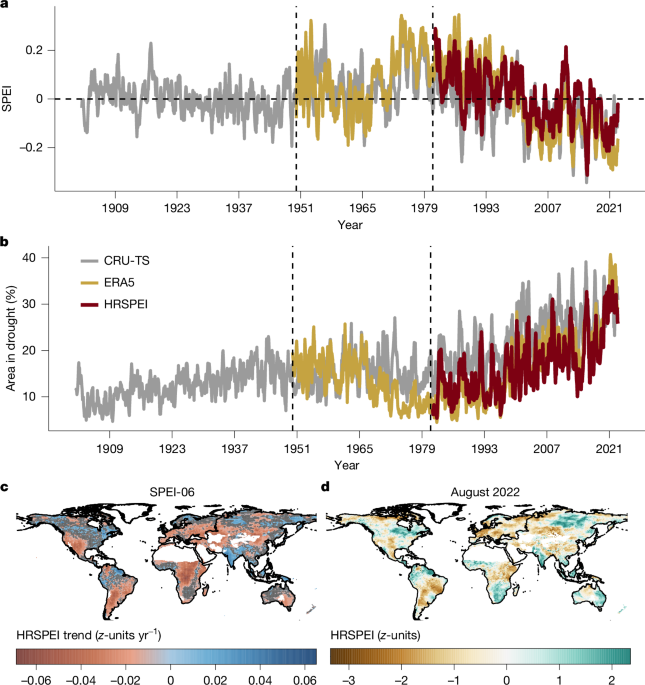
To assess the contributions of precipitation and AED, we developed additional indices based on observed (that is, actual values from hPET and GLEAM) AED with monthly climatological precipitation (Prclm), and observed (that is, a combination of gauge and satellite and reanalysis data) precipitation with climatological AED (AEDclm) for the period 1981–2022. Using AEDclm and Prclm allows us to quantify the impact of precipitation and AED changes and variability on droughts over the past 42 years. To further assess changes in drought during the early and mid-1990s, we developed two coarse-resolution SPEI indices based on ERA5 (0.25°) and CRU-TS (0.5°). The SPEI based on ERA5 was computed using monthly precipitation and AED derived from ERA5 meteorological datasets using the Penman–Monteith equation (equation (1)) for the period 1950–2022. Similarly, the SPEI based on CRU-TS was calculated using monthly precipitation and AED derived from CRU-TS meteorological datasets using the Penman–Monteith equation (equation (1)) for the period 1901–2022.

In this study, we use SPEI < −1 as the threshold to define a drought, with values between −1 and 1 considered near-normal conditions and values >1 indicating wet conditions (Extended Data Table 1). Using SPEI < −1 values, we assessed key drought metrics: magnitude, duration, intensity and frequency. We follow the classic approach and widely adopted methods to define these metrics⁴⁹. Drought magnitude is calculated as the cumulative sum (running total) of SPEI < −1 values during a drought event. Drought intensity is defined as the maximum negative value of SPEI observed during the event. Duration represents the run length of consecutive months with SPEI < −1, and frequency is the total number of drought events within a given period⁴⁹. Finally, severity is used as an overarching term to refer to all aspects of drought: intensity, magnitude, duration and extent.

Global climate and AED datasets

The MSWEP (version 2.8) dataset offers global 3-hourly, daily and monthly precipitation estimates at a 0.1° spatial resolution from 1979 to present⁴¹. Similarly, the CHIRPS (version 2.0) dataset provides daily, decadal and monthly precipitation estimates over land, with a spatial resolution of 0.05° for latitudes below 50°, covering the period from 1981 to present⁴⁰. Both MSWEP and CHIRPS are high-resolution precipitation datasets developed by integrating ground-station observations, satellite data and reanalysis products.

CHIRPS and MSWEP were chosen as they generally outperform other similar gridded precipitation datasets when compared with ground observations^29,30. CHIRPS (0.05°) is particularly designed for monitoring droughts and detecting environmental changes, providing daily precipitation estimates from 1981 to present. It combines satellite-derived Climate Hazards Center Infrared Precipitation (CHIRP) and the Climate Hazards Group Precipitation Climatology (CHPclim) with ground-station data from the Global Historical Climate Network and many other sources. The CHIRPS product benefits from a high degree of homogeneity, provided by its simple but consistent foundation of geostationary thermal infrared satellite observations. CHIRPS also incorporates unique observation inputs from Africa, Latin America and Central America. MSWEP (0.1°) has been designed with both accuracy and homogeneity in mind, providing 3-hourly precipitation estimates from 1979 to present. It integrates daily observations from over 77,000 stations from various national and international data sources, satellite estimates from infrared- and microwave-based satellite datasets, and reanalysis data, offering accurate global precipitation data from 1979 to present. Both CHIRPS and MSWEP have previously been evaluated globally using statistical metrics such as Kling–Gupta efficiency and Nash–Sutcliffe efficiency, as well as various bias and error metrics^29,30. For instance, MSWEP outperformed 22 other global precipitation datasets in capturing daily precipitation from 76,086 gauging stations and in driving hydrological models across 9,053 catchments²⁹. In addition, both MSWEP and CHIRPS were found to outperform other high-resolution gauge-based datasets in modelling daily, monthly and annual streamflow across 1,825 streamflow gauges³⁰. However, both datasets remain subject to inherent uncertainties, and, therefore, considering both helps reduce biases and obtain more reliable estimates, given that they are somewhat independent. For example, they differ in their data sources, with CHIRPS using only geostationary thermal infrared observations, whereas MSWEP also uses microwave observations, and they use different sets of station data to correct locally. Despite these differences, the monthly correlation between MSWEP and CHIRPS shows a high correlation across most regions, except for Central Asia (Extended Data Fig. 9a). The average monthly difference between the 2 datasets varies spatially, reaching up to ±40 mm (Extended Data Fig. 9d). Notably, larger discrepancies occur in regions such as the Amazon, Central Africa and parts of Southeast Asia. Such convergence between the two products helps reduce concerns about the uncertainties owing to different approaches and changes in the constellation of Earth-observing satellites that can affect the robustness of their representation of changes over time.

The hPET is a global hourly AED dataset developed using ERA5 climate datasets and the Food and Agriculture Organization (FAO)’s Penman–Monteith equation (equation (1)). hPET is available for the global land surface at 0.1° spatial resolution covering the period 1981–2022⁴³. In addition, the AED from GLEAM (version 4.2a) is a global dataset derived using Penman’s original equation (equation (2)), using satellite and reanalysis datasets⁴². GLEAM is available at a 0.1° spatial resolution and covers the period 1980–2023. hPET is based on the FAO Penman–Monteith equation, which computes reference crop evaporation by assuming certain surface and aerodynamic characteristics that are constant in time. In contrast, GLEAM calculates aerodynamic conductance as a dynamic variable depending on ecosystem characteristics and local meteorology and therefore is space and time dependent. Nonetheless, given the dominant influence of radiative forcing and atmospheric aridity in both computations, their estimates are overall similar. The correlation between GLEAM and hPET exceeds 0.9 across 91% of the global land surface (Extended Data Fig. 9b), and the monthly average difference between them is up to ±3 mm (Extended Data Fig. 9c).

The global AED and precipitation data from the CRU-TS dataset are available at a spatial resolution of 0.5°, covering the period from 1901 to present⁵⁰. Similarly, the ERA5 reanalysis dataset, representing the fifth-generation reanalysis from the European Centre for Medium-Range Weather Forecasts (ECMWF), is available at a spatial resolution of 0.25° from 1940 to present⁵¹.

Atmospheric evaporative demand

The hPET is estimated using the FAO-56 Penman–Monteith equation (equation (1)), and the GLEAM PET (potential evapotranspiration, AED) is calculated using Penman’s equation, including aerodynamic conductance (equation (2)). In addition, the FAO-56 Penman–Monteith method is applied to calculate AED from ERA5 climate datasets for the period 1950–2022 and CRU-TS climate datasets for 1901–2022. The Penman and FAO-56 Penman–Monteith methods consider various meteorological variables such as wind speed, air temperature, radiation and humidity to estimate AED:

where Δ is the slope of the plot of saturation vapour pressure–temperature relationship, R_n is the net radiation, G is the soil heat flux, γ is the psychrometric constant, T is the mean daily air temperature at 2-m height, u₂ is the wind speed at 2-m height, (e_s − e_a) is the vapour pressure deficit of the air (difference between saturation vapour pressure and actual vapour pressure), ρ_a is the air density, c_p is the specific heat capacity of air at constant pressure, g_a is the aerodynamic conductance, and λ_v is the latent heat of vaporization.

Trend analysis

The trend in SPEI is assessed using the non-parametric Mann–Kendall test and Sen’s slope estimator. The Mann–Kendall test identifies upwards or downwards trends in the SPEI time series for each pixel. Sen’s slope estimator calculates the slope of change in the SPEI series by computing the median of all possible slopes between data points. This method provides a robust estimate of the trend, particularly in the presence of outliers or nonlinear patterns. To identify drought events at the pixel scale, we utilize SPEI categories (Extended Data Table 1). SPEI values less than −1.0 are used to identify areas affected by droughts. We evaluate the frequency, duration and magnitude of these drought events (SPEI < −1) by analysing the number of occurrences, the length of consecutive periods and the intensity of SPEI values during the period from 1981 to 2022.