Problem statement
We represent the observed state of the atmosphere and surface at a discrete time t as a multidimensional array \(X^t\in \mathbbR^V\times H\times W\), in which V is the total number of variables and H and W are the number latitude and longitude coordinates, respectively. The state can be split into surface (St) and atmospheric (At) components: Xt = (St, At), in which \(S^t\in \mathbbR^V_\rmS\times H\times W\) and \(A^t\in \mathbbR^V_\rmAC\times H\times W\) with VS the number of surface-level variables, VA the number of atmospheric variables and C the number of pressure levels. The goal is to predict a future state at time t′ > t. We learn a simulator \(\Phi :(\mathbbR^V\times H\times W)^2\to \mathbbR^V\times H\times W\), \(\Phi (X^t-1,X^t)=\widehatX^t+1\), which maps the observed states at the previous time Xt−1 and current time Xt to a predicted state \(\widehatX^t+1\) at the next time step. For predictions at later time steps, we repeatedly apply the simulator, producing an autoregressive roll-out:
$$\beginarrayr\Phi (X^t,\widehatX^t+1)\,=\,\widehatX^t+2,\\ \Phi (\widehatX^t+1,\widehatX^t+2)\,=\,\widehatX^t+3,\\ \,\,\,\,\,\vdots \\ \Phi (\widehatX^t+k-2,\widehatX^t+k-1)\,=\,\widehatX^t+k.\endarray$$
For a detailed description of the notation and problem statement, including the specific multidimensional array dimensions and variable definitions, see Supplementary Information Section A.
The Aurora model
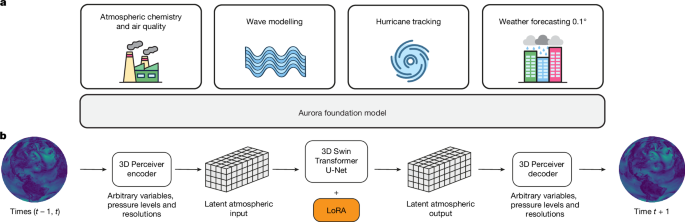
3D Perceiver encoder
To accommodate heterogeneous weather datasets with varying variables, pressure levels and resolutions, we design a flexible encoder that maps different datasets into a standardized 3D representation for input into the model backbone (Extended Data Fig. 3a).
The encoder treats all variables as H × W images. We incorporate static variables (orography, land–sea mask and soil-type mask) by treating them as extra surface-level variables. The images are split into P × P patches and the patches are mapped to embedding vectors of dimension D using variable-specific linear transformations. For the surface and every pressure level, the embeddings of different variables are summed and tagged with an additive encoding of the pressure level or a learned vector for the surface. A Perceiver module21 then reduces variable numbers of physical pressure levels C to a fixed number L = 3 of latent pressure levels. The result is a \(\fracHP\times \fracWP\times L\) collection of embeddings. This 3D representation is tagged with additive encodings for the patch position, patch area and absolute time. These encodings use a Fourier expansion scheme with carefully chosen minimum and maximum wavelengths to capture relevant information at appropriate scales. The patch area encoding enables Aurora to operate at different resolutions.
For a detailed description of the encoder architecture, including specifics on input processing, pressure-level aggregation and further encodings, see Supplementary Information Sections B.1 and B.4.
Multiscale 3D Swin Transformer U-Net backbone
The backbone of Aurora is a 3D Swin Transformer U-Net19,50, which serves as a neural simulator (see Fig. B1 Supplementary Information Section B.1). This architecture allows for efficient simulation of underlying physics at several scales. This architecture falls under the general family of Vision Transformers. However, unlike classical Vision Transformers, here we use local self-attention operations within windows and a symmetric upsampling–downsampling structure.
The backbone is characterized by the following key features: a symmetric upsampling–downsampling structure with three stages each, enabling multiscale processing; 3D Swin Transformer layers performing local self-attention operations within windows, emulating local computations in numerical integration methods; window shifting every other layer to propagate information between neighbouring regions while accounting for Earth’s spherical topology; res-post-norm layer normalization50 for increased training stability; and a flexible design allowing operation at several resolutions without fixed positional biases.
Our backbone contains 48 layers across three stages, compared with the 16 layers and two stages used in ref. 2. This increased depth is made possible by our efficient encoding procedure, which uses a small number of latent levels. For detailed information on the backbone architecture, including window sizes, attention mechanisms and comparisons with previous work, see Supplementary Information Section B.2.
3D Perceiver decoder
The decoder reverses the operations of the encoder, converting the output of the backbone, again a 3D representation, back to the normal latitude–longitude grid (see Fig. 6b). This involves disaggregating the latent atmospheric pressure levels using a Perceiver layer21 to any desired collection of pressure levels and dynamically decoding into patches by means of variable-specific linear layers. For a detailed description of the decoder architecture, see Supplementary Information Section B.3.
Training methods
The overall training procedure is composed of three stages: (1) pretraining; (2) short-lead-time fine-tuning; and (3) roll-out (long-lead-time) fine-tuning. We provide an overview for each of these stages in the following.
Training objective
Throughout pretraining and fine-tuning, we use the MAE as our training objective \(\mathcalL(\widehatX^t,X^t)\). Decomposing the predicted state \(\widehatX^t\) and ground-truth state Xt into surface-level variables and atmospheric variables, \(\widehatX^t=(\widehatS^t,\widehatA^t\,)\) and Xt = (St, At) (see Supplementary Information Section A), the loss can be written as
$$\beginarrayl\mathcalL(\widehatX^t,X^t)=\frac\gamma V_\rmS+V_\rmA\left[\alpha \left(\mathop\sum \limits_k=1^V_\rmS\fracw_k^\rmSH\times W\mathop\sum \limits_i=1^H\mathop\sum \limits_j=1^W| \widehatS_k,i,j^t-S_k,i,j^t| \right)\right.\\ \,+\left.\beta \left(\mathop\sum \limits_k=1^V_\rmA\frac1C\times H\times W\mathop\sum \limits_c=1^Cw_k,c^\rmA\mathop\sum \limits_i=1^H\mathop\sum \limits_j=1^W| \widehatA_k,c,i,j^t-A_k,c,i,j^t| \right)\right],\endarray$$
(1)
in which \(w_k^\rmS\) is the weight associated with surface-level variable k, \(w_k,c^\rmA\) is the weight associated with atmospheric variable k at pressure level c, α is a weight for the surface-level component of the loss, β is a weight for the atmospheric component of the loss and γ is a dataset-specific weight. See Supplementary Information Section D.1 for more details.
Pretraining methods
All models are pretrained for 150,000 steps on 32 A100 GPUs, with a batch size of one per GPU. We use a (half) cosine decay with a linear warm-up from zero for 1,000 steps. The base learning rate is 5 × 10−4, which the schedule reduces by a factor of ten at the end of training. The optimizer we use is AdamW51. We set the weight decay of AdamW to 5 × 10−6. The only other form of regularization we use is drop path (that is, stochastic depth)52, with the drop probability set to 0.2. To make the model fit in memory, we use activation checkpointing for the backbone layers and we shard all of the model gradients across the GPUs. The model is trained using bf16 mixed precision. See Supplementary Information Section D.2 for further details.
Short-lead-time fine-tuning
After pretraining Aurora, for each task that we wish to adapt Aurora to, we start by fine-tuning the entire architecture through one or two roll-out steps (depending on the task and its memory constraints). See Supplementary Information Section D.3 for more details.
Roll-out fine-tuning
To train very large Aurora models on long-term dynamics efficiently, even at high resolutions, we develop a new roll-out fine-tuning approach. Our approach uses low-rank adaptation (LoRA)53 to fine-tune all linear layers in the backbone’s self-attention operations, allowing adaptation of very large models in a data-efficient and parameter-efficient manner. To save memory, we use the ‘pushforward trick’54, which propagates gradients only through the last roll-out step. Finally, to enable training at very large numbers of roll-out steps without compromising memory or training speed, we use an in-memory replay buffer, inspired by deep reinforcement learning55,56 (see Fig. D2 in Supplementary Information Section D.3). The replay buffer samples initial conditions, computes predictions for the next time step, adds predictions back to the replay buffer and periodically refreshes the buffer with new initial conditions from the dataset. For detailed roll-out protocols for each fine-tuning task, see Supplementary Information Section D.4.
Datasets
Aurora was trained and evaluated using a diverse set of weather and climate datasets, encompassing five main categories: analysis, reanalysis, forecast, reforecast and climate simulation datasets. This variety of data sources exposes Aurora to different aspects of atmospheric dynamics, reflecting variability in initial conditions, model parametrizations and chaotic dynamics. Key datasets used in our experiments include ERA5 reanalysis, HRES operational forecasts, IFS ensemble forecasts, GFS operational forecasts, GEFS ensemble reforecasts, CMIP6 climate simulations, MERRA-2 atmospheric reanalysis, as well as CAMS forecasts, analysis and reanalysis data. For a detailed inventory of all datasets used, including specific pressure levels, resolutions and further context for each dataset, see Supplementary Information Section C. These datasets vary in resolution, variables included and temporal coverage, providing a comprehensive basis for training, fine-tuning and evaluating the performance of Aurora across different scenarios.
Task-specific adaptations
Ocean wave forecasting
In the IFS HRES-WAM analysis data, there is a spatially varying absence of data reflecting the distribution of sea ice among other effects. To account for this dynamic nature of the spatial distribution of defined variables, we give each variable an extra channel to represent the presence of a measurement, so we add an extra set of density variables33 (see Supplementary Information Section B.8).
Data infrastructure
Training Aurora presented substantial technical challenges owing to the large size of individual data points (nearly 2 GB for 0.1° data) and the need to handle heterogeneous datasets with varying resolutions, variables and pressure levels. Owing to the size of data points, training is typically bottlenecked by data loading and not by the model. This means that training smaller models is not always cheaper, because training costs will be dominated by data loading. We developed a sophisticated data storage and loading infrastructure to address these technical challenges.
Data storage and preprocessing
We use Azure Blob Storage with several optimizations to ensure efficient data access. These optimizations include colocating data and compute to minimize latency and costs, storing datasets in appropriate chunks to avoid unnecessary data download and to minimize the number of concurrent connections and compressing these chunks to reduce network bandwidth.
Data loading
We have developed an advanced multisource data loading pipeline to efficiently handle heterogeneous data. We now outline the main design principles of our pipeline. Datasets are instantiated using YAML configuration files specifying loading parameters. Each dataset generates a stream of lightweight BatchGenerator objects. The scope of the BatchGenerator class is to abstract away the details and particularities of datasets by offering a common interface for generating data batches. The streams are combined, shuffled and sharded across GPUs. After sharding, finally the common interface of BatchGenerator is used to do the work needed to download and construct batches for training and inference.
This pipeline enables efficient training on several heterogeneous datasets by batching only samples from the same dataset together and automatically balances workloads across GPUs by using different batch sizes for different datasets. This design offers flexibility needed to experiment with the Aurora model architecture while efficiently handling the challenges of large-scale, heterogeneous weather data processing. For a detailed description of the data loading pipeline, including the BatchGenerator object structure and the unpacking process, see Supplementary Information Section E.
Verification metrics
We evaluate the performance of Aurora using two main metrics: the RMSE and the anomaly correlation coefficient. Both metrics incorporate latitude weighting to account for the non-uniform grid of the Earth. The RMSE measures the magnitude of errors between predictions and ground truth, whereas the anomaly correlation coefficient measures the correlation between the deviation of the prediction and ground truth from the daily climatology.
To assess performance on extreme weather events, we use a thresholded RMSE. The thresholded RMSE uses a threshold to determine which latitude–longitude grid points should be included in the calculation, allowing for evaluation of model performance across different intensity levels of weather phenomena. The thresholds are defined using the mean and standard deviation of the ERA5 reanalysis data over all training years computed separately for each latitude–longitude point. We vary these thresholds linearly for both positive and negative values to obtain RMSE curves for different intensity levels.
For a comprehensive explanation of the verification methods used in this work, including their mathematical formulation and interpretation, see Supplementary Information Section F. Taken together, the metrics used here provide a robust framework for evaluating the performance of Aurora across various weather conditions, from typical to extreme events.
Further details
Further details are available in the Supplementary Information and rely on refs. 26,46,57,58,59,60,61,62,63,64,65,66,67,68,69,70,71,72,73,74,75.