Global emergence of unprecedented lifetime exposure to climate extremes

ISIMIP and exposure projections

The Inter-Sectoral Impact Model Intercomparison Project (ISIMIP) provides a simulation protocol for projecting the impacts of climate change across sectors such as biomes, agriculture, lakes, water, fisheries, marine ecosystems and permafrost (www.isimip.org). In ISIMIP2b, impact models representing these sectors are run using atmospheric boundary conditions from a consistent set of bias-adjusted global climate models (GCMs) from phase 5 of the Coupled Model Intercomparison Project (CMIP5) that were selected based on their availability of daily data and ability to represent a range of climate sensitivities¹⁷; the Geophysical Fluid Dynamics Laboratory Earth System Model (GFDL-ESM2M; ref. ³⁰), the earth system configuration of the Hadley Centre Global Environmental Model (HadGEM2-ES; ref. ³¹), the general circulation model from the Institut Pierre-Simon Laplace Coupled Model (IPSL-CM5A-LR; ref. ³²) and the Model for Interdisciplinary Research on Climate (MIROC5; ref. ³³). Impact simulations are run for pre-industrial control (286 ppm CO₂; 1666–2099), historical (1861–2005) and future (2006–2099) periods. Future simulations are based on Representative Concentration Pathways (RCPs) 2.6, 6.0 and 8.5 of GCM input datasets. Global projections of annual, grid-scale fractions of exposure to each extreme event category are calculated from ISIMIP2b impact simulations and GCM input data. For the full details of these computations, we refer to ref. ¹², but we summarize extreme event definitions below.

For heatwaves, droughts, crop failures and river floods, we use localized pre-industrial thresholds to determine event occurrences, whereas for tropical cyclones, we use a single absolute threshold, and wildfires are modelled explicitly (Supplementary Table 20). Heatwaves affect an entire grid cell if the Heat Wave Magnitude Index daily (HWMId; refs. ^34,35) of that year exceeds a threshold in the pre-industrial control HWMId distribution in that grid cell¹¹. Although we refer to heatwaves throughout the paper, our definition technically refers to a 3-day extreme heat event that is expected on average once per century under pre-industrial climate conditions. These extreme heat events occur, by definition, everywhere across the world, but with different associated absolute temperature values. Previous analysis highlighted that intergenerational inequalities in lifetime heatwave exposure are robust across a range of heatwave definitions¹¹. Crop failures are based on the sum of the area occupied by maize, wheat, soy or rice within a grid cell when their simulated yield falls below a threshold of their pre-industrial reference yield. Droughts, such as heatwaves, affect an entire grid cell if, for 7 months, monthly soil moisture remains below a threshold of pre-industrial soil moisture levels. Floods only correspond to river flooding, and the flooded area is derived from comparing daily discharge simulations from models of the global water sector to pre-industrial discharge. CaMa-Flood, a global river-routing model³⁶, is used to convert these discharge values to flooded areas. Tropical cyclones occur if a grid cell sustains hurricane-force winds (≥64 knots) at least once a year^37,38. Exposure to tropical cyclones does not encompass the flood hazards typically associated with tropical cyclones. Wildfires occur when the burnt area is simulated in a grid cell. Burnt area is either taken directly from annual burnt area calculations or as the annual sum of monthly burnt area in cases in which impact models simulate burnt area sub-annually, capped at 100% of a grid cell. We reiterate that all exposure definitions here neglect potential exposure reduction measures and non-local effects.

We subsequently quantify human exposure to climate extremes in a way that facilitates comparison and aggregation across extreme event categories. We consider all people in a grid cell exposed to a climate extreme in a particular year if the climate extreme occurs in that year. We thereby assume that if such a river flood or wildfire occurs somewhere in a 0.5° × 0.5° grid cell, this is sufficiently close to any person located in that grid cell to be considered affected by this extreme event. Using demographic data (see below), we subsequently convert this annual human exposure to lifetime exposure of birth cohorts by summing annual grid fractions of individual event categories across their lifetimes.

Demographics

Demographic data for population totals, cohort sizes and life expectancy enable our projection of the CF experiencing ULE to these six extremes. Population totals at the grid scale come from the ISIMIP database (Fig. 2b; ref. ¹⁷) and originate from population estimates from v.3.2 of the History Database of the Global Environment (HYDE3.2; refs. ^39,40) for the historical period (1860–2000) and population projections from middle-of-the-road Shared Socioeconomic Pathway (SSP2; refs. ^41,42) for the future period (2010–2100). We note that these datasets at present do not account for the impact of climate on population dynamics, for example, through changes in migration, fertility and mortality, although these feedbacks may substantially alter the demographic data. Cohort sizes from the Wittgenstein Centre for Demography and Global Human Capital⁴³ provide estimates of country-level population totals every 5 years (between 1950 and 2100) for each 5-year age group (0- to 4-year-olds, 5- to 9-year-olds, and so on, until 95- to 99-year-olds and a final age group for those 100 years and older). Life expectancy data come from the United Nations World Population Prospects (UNWPP; ref. ⁴⁴) and describe the life expectancy of 5-year-olds at the country level for 5-year blocks (1950–1955 to 2015–2020). In this dataset, life expectancy is reported for 5-year-olds to exclude biases from infant mortality. Countries that can be spatially resolved at the ISIMIP grid scale and have cohort and life expectancy estimates in these datasets meet the requirements of this study and total 177. We refer to the supplementary material of ref. ¹¹ for a broader discussion of these datasets but explain our application of them in this analysis below.

All demographic datasets are modified to represent lifetimes annually, beginning from 1960 to 2020. Life expectancies for each country are first linearly interpolated to annual values by assuming that the values of the original 5-year groups are representative of the middle of that group. Furthermore, we add 5 years to annual life expectancies to capture the life expectancy of each cohort since birth, as the original data begin at age 5. As the maximum UNWPP life expectancy for people born in 2020 prescribes the final year in this analysis (2113), annual population totals must be extrapolated to reach this year. For population totals, we take each year beyond 2100 as the mean of the preceding 10 years of the dataset, such that population numbers for 2101 are the mean of 2091–2100. For cohort sizes in each country, we interpolate annual cohort sizes and age groups from the original 5-year age groups and divide age totals by 5 to maintain original population sizes in this dataset and linearly extrapolate these estimates to 2113. This provides the absolute numbers of 0- to 100-year-olds for each year across 1960–2113.

To downscale this demographic information to the grid scale, we assume spatially homogeneous cohort representation and life expectancy. Birth cohort size is represented as the number of people of age 0 of a given birth year in a given grid cell. This is estimated by multiplying the absolute population of the birth year (using the annual grid-scale population totals from ISIMIP) by the relative size of the age 0 cohort (using the interpolated 0- to 100-year-old population totals from the Wittgenstein Centre cohort data). Spatial variability in age structure and life expectancy within a country is therefore ignored in this study.

Mapping impacts to GMT trajectories

To project CF across different warming pathways by 2100, we construct a series of incrementally warming GMT pathways between 1960 and 2113 based on GMT trajectories taken from the AR6 Scenario Explorer⁴⁵. The time series from the AR6 scenario explorer were chosen as anchor points for interpolation to produce a range of plausible GMT time series. Furthermore, they were selected to minimize overshooting in the early years of low GMT pathways over higher GMT pathways, which can skew lifetime exposure estimates for early birth cohorts (Supplementary Fig. 9). The upper bound of this subset was limited to 3.5 °C in favour of sampling more simulations for higher GMT projections, which we discuss further below. For the lower bound, 1.5 °C was chosen because it is a more realistic minimal warming scenario than 1.0 °C. Note that the 1.5 °C anchor scenario maximally reaches 1.57 °C before reducing to 1.5 °C by 2100. It is, therefore, referred to as 1.5 °C throughout this analysis. These warming levels are reported relative to pre-industrial temperatures from 1850 to 1900. This yields a total of 21 GMT pathways for which we project CF.

Our dataset of extreme event exposures represents occurrences of these extremes forced by GCM-modelled climates. These climates have unique GMT warming pathways that depend on their radiative forcing scenario (historical or RCP), as prescribed by the ISIMIP2b modelling protocol. To project these exposure maps along even intervals of warming scenarios, which the original simulations do not provide, we use the 21 GMT pathways described above. For each pairing of the 21 target GMT pathways and the concatenated historical and future exposure projections, we sample exposures by matching the GMT warming levels of the exposure series to the years of the target GMT pathways (Supplementary Figs. 9 and 10). The GMT warming levels behind the exposure projections are first smoothed with a 21-year rolling mean before GMT mapping is undertaken. In cases in which our constructed GMT pathways exceed the GMT warming levels of GCM simulations by too much, this mapping erroneously resamples the year of exposures corresponding to the maximum warming level of their forcing GCM. To this end, we implement a constraint in this sampling procedure such that GMT-mapped series are only used if the maximum difference across all GMT pairs is no larger than 0.2 °C. This constraint incrementally reduces ensemble sizes of exposure projections for higher GMT pathways (Supplementary Table 19).

Lifetime exposure

Estimating lifetime exposure to extreme events requires crossing life expectancy data at the country level with grid-scale exposure projections. For each GMT trajectory (1.5–3.5 °C, 0.1 °C intervals), birth year (1960–2020) and country (177), exposures are summed across lifetimes at the grid scale. This assumes life expectancy to be spatially homogeneous across each country. Exposure during the death years is also included in this sum by multiplying these exposure projections by the fraction of the final year lived. This produces country-wide maps of lifetime exposure at the grid scale for each GMT trajectory and birth year in this analysis.

To generate a baseline distribution of lifetime exposure in a world without climate change, large samples of pre-industrial lifetime exposures are bootstrapped assuming 1960 life expectancy in each country. Here, for each exposure projection originating from a simulation under a pre-industrial climate, 10,000 lifetime exposures are estimated by resampling exposure years with replacement. Depending on ISIMIP2b data availability, pre-industrial exposure projections have a length of 239–639 years per simulation from which to resample from¹¹. This process generates 40,000–310,000 country-wide maps of lifetime exposure, depending on the extreme event considered and its underlying data availability, enabling exposure projections in a pre-industrial climate. Using the pre-industrial period as a baseline enables (1) our GMT mapping procedure; (2) bootstrapping a stationary time series to achieve a large reference dataset; and (3) the production of a reference dataset with information that is independent of the projections forming our ULE estimates.

Emergence of ULE

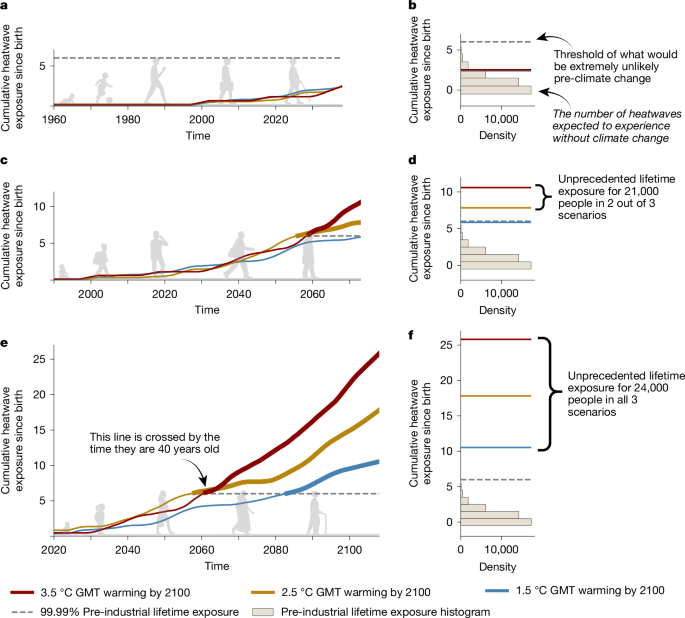
We define an emergence threshold for ULE to extreme events as the 99.99th percentile of our grid-scale samples of pre-industrial lifetime exposure. When it comes to the selection of this percentile, we went as extreme as possible given the bootstrapping of the pre-industrial control runs. This choice was based on a sensitivity analysis for different percentile values that showed a levelling off of lifetime exposure for percentiles more extreme than 99.99%. This indicated that the 99.99th percentile achieves the limit of reliable information that can be extracted from the empirical distribution. For each extreme event, birth year, GMT pathway and grid cell, we assess if lifetime exposure emerges or passes this threshold of extreme exposure in a pre-industrial climate. If this threshold is passed, we consider the whole birth cohort in this grid cell to have emerged, tallying its size among a global pool of the same birth cohort and GMT trajectory of people projected to live ULE. This means that, in some locations, even if the sum of exposed grid cell fractions across a pre-industrial lifetime does not cover the entire grid cell, we still extract the entire birth cohort size associated with that grid cell. We sum the number of emerged people in each birth cohort globally, although this birth cohort has a different life expectancy in each country. Once the number of people who have emerged globally is tallied, we divide this by the respective total cohort sizes to estimate CF per birth cohort. Note that ULE, therefore, does not refer to unprecedented in terms of the magnitude of assets or people exposed, but rather in terms of the number of events accumulated across an average person’s lifespan in comparison with what they would face in a pre-industrial climate.

ULE across socioeconomic vulnerability strata

We use two grid-scale indicators of vulnerability to compare with our estimates of ULE to heat waves. The first is an ISIMIP2b GDP input dataset using concatenated historical and SSP2 time series covering 1860–2099 annually¹⁷. This dataset was disaggregated from the country to grid level using spatial and socioeconomic interactions among cities, land cover and road network information and SSP-prescribed estimates of rural and urban expansion⁴⁶. The second indicator is the Global Gridded Relative Deprivation Index v.1 (GRDI; ref. ¹⁶), which communicates relative levels of multidimensional deprivation and poverty (0–100, least to most deprived). This deprivation score uses six input components. First is the child dependency ratio, which is the ratio between the population of children and the working-age population (15–64 years). This can indicate vulnerability, for which high ratios indicate a dependency of supposed consumers and non-producers on the working-age (producing) population⁴⁷. Second, infant mortality rates (IMR), taken as the deaths in children younger than 1 year of age per 1,000 live births annually, are a signal of population health and form a long-term Sustainable Development Goal of the United Nations⁴⁸. Third, the Subnational Human Development Index (SHDI), an assessment of human well-being across education, health and standard of living, originates from the Human Development Index, the latter of which is considered one of the most popular indices to assess country-level well-being. The SHDI improves on the HDI in terms of spatial scale and in representing 161 countries across all world regions and development levels⁴⁹. Fourth, as rural populations are generally prone to multidimensional poverty⁵⁰, low values in the ratio of built-up to non-built-up area (BUILT) signal high deprivation. The fifth and sixth components use the mean (of 2020; VNL 2020) and slope (2012–2020; VNL Slope) of nighttime light intensity, a proxy for human activity, economic output and infrastructure development⁵¹, to indicate deprivation for areas of low nighttime light intensity. These input components range from 30 arc seconds (roughly 1 km) resolution to subnational regions and are harmonized in an ArcGIS Fishnet feature class for aggregation onto a 0–100 range representing low to high deprivation. For the final aggregation, the IMR and SHDI components are given half the weight of the rest of the inputs, given their coarser resolution. The GRDI, therefore, encapsulates multiple dimensions through which generations face deprivation and therewith socioeconomic vulnerability to climate extremes. Although our approach does not explicitly account for actual or potential adaptation to climate change, this multidimensional approach to vulnerability provides relevant information on the current adaptation potential of local populations.

We preprocess GDP and GRDI products to enable their comparison with our ULE estimates across birth years. For GDP, similar to other datasets in our analysis, we extend the series to 2113 to accommodate the longest life expectancy of the 2020 birth cohort by copying the final year of the original dataset. We then use our ISIMIP population totals to compute GDP per capita at the grid scale. Using the GDP per capita metric, we calculate lifetime mean GDP per capita using our life expectancy information for the 1960–2020 birth cohorts. We refer to lifetime mean GDP per capita as simply GDP. For GRDI, we conservatively regrid the original grid cells of  about 1 km to the 0.5° ISIMIP grid. Although GRDI is a map composed of data spanning 2010–2020, we assume this to be representative of 2020, but nonetheless compare it with the 1960–2020 birth cohort range, similar to the rest of the analysis.

We then identify 20% quantile ranges (that is, (0–20], (20–40], … (80–100]) for the lifetime GDP of each birth year and for the singular GRDI map (assumed to align with 2020 population totals). To this end, we rank the vulnerability indicators and apply these ranks to our birth cohort totals on the same grid and for the matching year. For example, the ranks taken from the lifetime mean GDP of the 2020 birth cohort are aligned with the population totals of newborns in 2020. Finally, we bin the ranked vulnerability indicators by their associated population totals into five groups of nearly equal population (as it is not possible to achieve perfect bin sizes given the sums of grid-scale population totals). This groups the richest and poorest and least and most deprived into the aforementioned quantile ranges. The quantile range of each vulnerability indicator is then a map that can be used to mask the existing locations of ULE, such as birth years and all GMT pathways. With GRDI (Supplementary Fig. 11) and GDP (Supplementary Fig. 12), we compare the lowest and the highest 20% of each indicator by population.