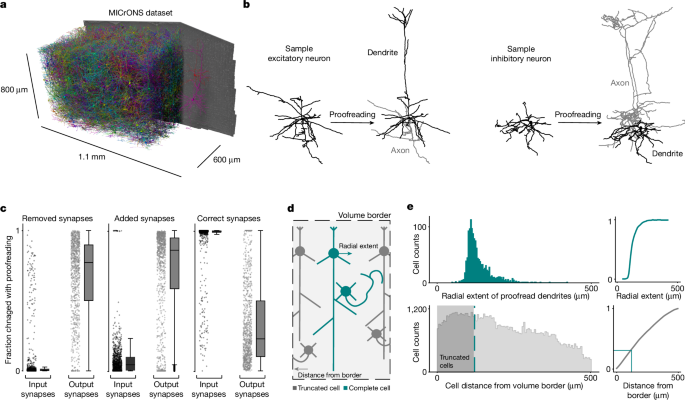
MICrONS dataset
This dataset consists of a 1.1 mm × 800 µm × 600 µm segmentation of a volumetric serial-section electron microscopy dataset from mouse visual cortex of a male postnatal day 87 (P87) mouse. The dataset covers all layers of cortex and spans primary visual cortex and two higher visual areas. The dataset has been described in detail elsewhere5. Briefly, two-photon imaging was carried out on the mouse, which was subsequently prepared for electron microscopy. The specimen was then sectioned and imaged using transmission electron microscopy6. The images were then stitched, aligned and processed through a deep learning segmentation algorithm, followed by manual proofreading5,6,7,15.
Cortical column
In this manuscript, we leveraged proofreading that was carried out and labels that were prepared as part of a separate study of a 100-µm columnar region of primary visual cortex within the larger dataset15. For clarity and completeness, we repeat some aspects of the methods that define that column here.
Column selection
The column borders were found by manually identifying a region in the primary visual cortex that was as far as possible from both the volume boundaries and the boundaries with higher-order visual areas. A 100 × 100 µm box was placed on layer 2/3 and was extended along the y axis of the dataset. While analysing the data, it was observed that deep-layer neurons had apical dendrites that were not oriented along the most direct pia-to-white-matter direction, and thus we adapted the definition of the column to accommodate these curved neuronal streamlines. Using a collection of layer 5 ET cells, points were placed along the apical dendrite to the cell body and then along the primary descending axon towards the white matter. The slant angle was computed as two piecewise linear segments, one along the cortical depth to lower layer 5 where little slant was observed, and one along the direction defined by the vector-averaged direction of the labelled axons.
Using these boundaries and nucleus centroids5, all cells were identified inside the columnar volume. Coarse cell classes (excitatory, inhibitory and non-neuronal) were assigned on the basis of brief manual examination and rechecked by subsequent proofreading and confusion analysis with early versions of the classifiers described here. To facilitate concurrent analysis and proofreading, all false merges that connected any column neurons to other cells (as defined by detected nuclei) were split.
Proofreading
Proofreading was carried out by five expert neuroanatomists using the Connectome Annotation Versioning Engine56,57 and a modified version of Neuroglancer58. Proofreading was aided by on-demand highlighting of branch points and tips on user-defined regions of a neuron based on rapid skeletonization (https://github.com/AllenInstitute/Guidebook). This approach quickly directed proofreader attention to potential false merges and locations for extension, as well as allowing a clear record of regions of an arbour that had been evaluated.
For dendrites, all branch points were checked for correctness and all tips were examined to determine whether they could be extended.
False merges of simple axon fragments onto dendrites were often not corrected in the raw data, as they could be computationally filtered for analysis after skeletonization (see below). Detached spine heads were not comprehensively proofread, and previous estimates place the rate of detachment at approximately 10–15%.
For inhibitory axons, axons were ‘cleaned’ of false merges by looking at all branch points. Axonal tips were extended until either their biological completion or data ambiguity, particularly emphasizing all thick branches or tips that were well suited to project to new laminar regions. For axons with many thousands of synaptic outputs, some but not all tips were followed to completion once main branches were cleaned and established. For smaller neurons, particularly those with bipolar or multipolar morphology, most tips were extended to the point of completion or ambiguity. Axon proofreading time differed substantially by cell type, not only because of differential total axon length, but also because of axon thickness differences that resulted in differential quality of auto segmentations, with thicker axons being of higher initial quality. Typically, inhibitory axon cleaning and extension took 3–10 h per neuron. Expert neuroanatomists further labelled excitatory and inhibitory neurons into subclasses. Layer definitions were based on considerations of cell body density (in analogy with nuclear staining) supplemented by identifying kinks in the depth distribution of nucleus size near expected layer boundaries.
Cell labelling
For excitatory neurons, the categories used were: layer 2/3 IT, layer 4 IT, layer 5 IT, layer 5 ET, layer 5 NP, layer 6 IT and layer 6 CT cells. Layer 2/3 and upper layer 4 cells were defined on the basis of dendritic morphology and cell body depth. Layer 5 cells were similarly defined by cell body depth, with projection subclasses distinguished by dendritic morphology following ref. 2 and classical descriptions of thick (ET) and thin-tufted (IT) cells. Layer 5 ET cells had thick apical dendrites, large cell bodies, numerous spines and a pronounced apical tuft, and deeper ET cells had many oblique dendrites. Layer 5 IT cells had more slender apical dendrites and smaller tufts, fewer spines and fewer dendritic branches overall. Layer 5 NP cells corresponded to the ‘spiny 10’ subclass described in ref. 2; these cells had few basal dendritic branches, each very long and with few spines or intermediate branch points. Layer 6 neurons were defined by cell body depth, but only some cells were able to be labelled as IT or CT by human experts. Layer 6 pyramidal cells with stellate dendritic morphology, inverted apical dendrites or wide dendritic arbours were classified as IT cells. Layer 6 pyramidal cells with small and narrow basal dendrites, an apical dendrite ascending to layer 4 or layer 1, and a myelinated primary axon projecting into white matter were labelled as CT cells.
Basket cells were recognized as cells that made more than 20% of their synaptic inputs onto the soma or proximal dendrites of cells. Neurogliaform cells were recognized by having a low density of output synapses, and boutons that often had synaptic vesicles but no postsynaptic structures. Bipolar cells were labelled by having only 2 or 3 primary dendrites, and primarily making synapses with other inhibitory neurons. Note that the Martinotti/non-Martinotti subclass label was given to cells that have previously been described in the literature to primarily target the distal dendrites of excitatory neurons without exhibiting hallmark features of bipolar or neurogliaform cells.
Owing to high levels of proofreading in the column, there were very few errors; thus, the training set was augmented with manually labelled errors from the entire dataset.
Proofreading and truncation analysis
For every proofread cell in the cortical column (described above), we compared the cellular volume of the initial reconstruction from the automated segmentation to the cleaned and completed reconstruction. To measure the precision connectivity for each cell, we noted the number of synapses that got removed with proofreading, the number of synapses that were added, and the number of synapses that were maintained with each cell before and after proofreading.
To estimate the likelihood of truncation, we measured the distribution of dendritic extents from the proofread column cells. For each cell, we measured the radial distance of each input synapse from the cell’s soma. For each cell, the distance from the soma of every input synapse was calculated and the radial extent was defined as the 97th percentile of this distribution. From a distribution of these measurements across all cells, we used the median value of 121 µm as a threshold for dendritic truncation, although closer to 250 µm would be required to guarantee no truncation for any cell. For the rest of the cells in the dataset, we measured the distance of the soma from the volume borders in x and z. The overlap in these distributions relates to the probability of truncation, leading to our conclusion that roughly one-third of the cells have some degree of dendritic truncation.
Generating nucleus and soma features
We analysed nuclei using the results of a deep neural network segmentation5, extracted the mesh using marching cubes and obtained the largest component of the detected mesh. Nuclear features were then extracted on the remaining meshes. These features included nucleus volume, nucleus area, the area-to-volume ratio, nucleus surface area within an infolding, the fraction of the total surface area within an infolding, and cortical depth (measured as the distance from the pial surface). Nucleus fold features were extracted by creating a shrink-wrapped47 mesh for each nucleus mesh. We then calculated the distance of each vertex on the nucleus mesh from the shrink-wrapped mesh. After visual inspection of cells across all of the reported subclasses, any vertex further than 150 nm was considered to be within an infolding.
For each nucleus detection, the somatic compartment was identified as the ID in the segmentation that surrounded >80% of the nucleus. Somatic segmentations (downloaded at 64 × 64 × 40 nm resolution) went through a heuristic cleaning procedure to remove missing slices of data and incorrectly merged fragments. As each soma was matched to its corresponding nucleus, 15 µm surrounding the nucleus’s centre of mass was cut out from the dense segmentation and converted into a binary mask. The value of 15 µm was chosen owing to the high quality of the segmentation (Fig. 2a) and it was large enough to encompass the entire soma of all cells from the smallest glial cell to the largest 5P-ET neuron. Binary dilation by five voxels in three dimensions was carried out, followed by filling of all holes, and then binary erosion of three voxels. The resulting binary mask was meshed using marching cubes and connected component analysis was run on the result. The value of five voxels was deemed an appropriate dilation to remove merged fragments without creating additional holes in the mesh. The largest connected component mesh was retained, and any disconnected components were dropped. Somatic features were extracted for all nuclear detections that were not cut off by the volume boundary (see the section entitled Filtering procedure). These somatic features included soma area, soma volume, the area-to-volume ratio, the number of synapses on the somatic cutout and the soma synapse density. Using both the somatic and nucleus meshes, we calculated the ratio between the nucleus volume and soma volume and the offset between the two, measured as the Euclidean distance between the nuclear centre of mass and the soma centre of mass.
Filtering procedure
There were 133,580 nuclear detections in the dataset, and the filtering procedure consisted of three steps. First, any detected objects less than 25 µm3 were filtered out as errors as these largely consisted of small fragments of nucleoli. Second, after identifying the segment IDs within a 15-μm bounding box around each nucleus, if more than 20% of these IDs corresponded to error ID 0, they were filtered out. Most of these error cases were cells close to the volume border or areas in the volume with higher segmentation errors such as those near blood vessels. Third, cells that were predicted as errors by the object classifier of the hierarchical model described below (model 1 in Fig. 5a) were also removed from analysis. This resulted in a final set of 94,010 cells, neuronal and non-neuronal.
Feature normalization
Owing to differences in section thickness during sample preparation, we noticed abrupt shifts in nucleus and soma size features along the sectioning axis (z plane). This presumably is due to changes in section thickness across the dataset. To account for these abrupt and systematic shifts, we binned the entire dataset by the longest length scale for which there did not seem to be systematic shifts in the distribution in the z plane (800 nm) and normalized each feature value by the average within each z bin.
For 2D UMAP embeddings and training of the classifiers, it was important to place all features in approximately similar scales. For this reason, we independently z-scored each feature across all cells and used that as the input for classifier training as well as the UMAP embeddings in Figs. 3–6.
Generating PSS features
Around each synapse, we extracted a 3,500-nm region to obtain the synapse region mesh. We experimented with region cutouts between 1,000 and 5,000 nm; however, smaller cutouts led to ambiguities in the main shaft identification and thereby produced errors in the subsequent skeletonization. At 3,500 nm, the skeletons were more stable and segmented as expected. This mesh was then segmented using the CGAL surface segmentation algorithm59, which splits regions on the basis of differences in thickness. We adapted our previously developed method24 to identify the PSS region by using a local skeleton calculated from the synapse region mesh, rather than a precomputed whole-cell mesh. This allowed us to adapt this method for cells in the dataset without the need for proofreading.
Given a cell for which all PSSs have been extracted within a 60 µm radius from the nucleus centre, the objective was to build a descriptor that encapsulates the various properties of the PSS. In particular, we aim to capture two of these properties: the type of shape of the PSS and the distance of the PSS from the soma. Moreover, as different cells can have different numbers of shapes (synapses), we needed a fixed-size representation for each cell. To capture shape information, a dictionary of all shape types was built using a dictionary dataset from 236,000 PSSs from a variety of neurons24. These shapes were rotationally normalized and used to train a PointNet autoencoder60,61 to learn a latent representation of size 1,024. The high-dimensional latent space spanning all of these shapes is a continuous space (Extended Data Fig. 3), which was used to generate a bag of words model30 for the shapes. To ensure that we were sampling the entire embedding space, we carried out k-means clustering with k = 30 to estimate cluster centres. We manually reordered the bin centres for visualization purposes from shapes representing small spines, to those representing longer spines, to dendritic shafts of different shapes, and finally somatic compartments. The top row of the right panel of Fig. 4d shows the shape in the dictionary that is closest to each of these cluster centres. For distance from the soma, we split the 60 µm radius around the nucleus centre into four 15-µm radial bins (Fig. 4c,d). All PSSs were then binned according to their shape and distance properties to generate a histogram of counts. Initially we extracted PSSs from within 120 µm radius. However, on inspection of the normalized histograms and the 2D UMAP embedding space, the additional radial bins did not increase our differentiability and did increase truncation effects near the dataset; thus, we reduced the radius to 60 µm. Finally, this histogram was z-scored and then added to the rest of the features as input to classifiers and the UMAP embedding (Figs. 4 and 6).
Hierarchical model training and validation
Hierarchical framework
We defined an object as the segmentation associated with a predicted nucleus5 from which nucleus, soma and PSS features could be extracted. A hierarchical framework was designed to predict the cell type of any such object (Fig. 5c). To begin, there were 106,761 nuclear segmentations that passed the first 2 filters described above (see the section entitled Filtering procedure). The first level in the hierarchy predicted whether an object was a neuron (72,158), non-neuron (21,856) or an error (12,751). All objects predicted as errors were excluded from all subsequent analyses except for the hierarchical model evaluation. Non-neuronal cells were then classified as one of the following: astrocyte (7,850), microglia (2,638), oligodendrocyte (7,020), oligodendrocyte precursor cell (OPC; 1,703) or pericyte (2,645). For neurons, cells were predicted as either excitatory (64,195) or inhibitory (7,963) followed by a separate subclass classifier for each class type. Excitatory subclasses were layer 2/3 pyramidal (19,735), layer 4 pyramidal (14,777), layer 5 IT (7,949), layer 5 ET (2,215), layer 5 near-projecting (NP) pyramidal (970), layer 6 IT (11,734) and layer 6 CT pyramidal (6,815). After extracting PSS features from all predicted inhibitory neurons, a subset of neurons (n = 1,158) that were actually excitatory clearly separated from the rest of the cells in the perisomatic feature space (with PSS features). This was expected owing to known differences in proximal dendrite morphology between inhibitory and excitatory neurons. These neurons were then passed through the excitatory neuron classifier and labelled as excitatory for all subsequent analyses with a final set of 6,805 inhibitory cells with the following subclass counts: basket cells (3,239), bipolar cells (997), Martinotti/non-Martinotti cells (1,992) and neurogliaform cells (571).
Training
Soma and nucleus features were extracted from the 3D mesh of all objects and PSS features were extracted for all neurons predicted as inhibitory. For each level of the hierarchy, multiple classifiers were trained using either nucleus alone, nucleus and soma features, or nucleus, soma and PSS features. Within each level of the hierarchy, classifiers were trained using the cells and labels from the manually annotated cortical column. Owing to the sparsity of some of the cell classes, we augmented the training set in the following ways: 470 errors were added from within and around the column for the object model; 11 proofread 5P-NP cells and 250 proofread 5P-ET cells were added to train the excitatory subclass model.
For each classifier, the model type was chosen using a randomized grid search for the following models: support vector machine with a linear kernel, support vector machine with a radial basis function kernel, nearest neighbours, random forest classifier, decision tree and neural network. For each type, 50 models were trained with varying parameters and the top-performing model was chosen. Individual models were further optimized using tenfold cross-validation evaluated on the basis of accuracy and F1 score (a measure for precision and recall). Training and test examples were held consistent across models for direct performance comparison within each level.
Model performance and validation
The hierarchical model was defined as the sequential combination of the best-performing classifiers at each level. To see the performance of all different feature sets at each level of the hierarchy, see Extended Data Table 1. The overall performance of the hierarchical model was measured with a test set that involved manual inspection of 100 examples of each of the neuronal and non-neuronal subclasses as well as errors. This resulted in a test set of 1,700 cells. Cross-validation and test performance for the hierarchical model are reported below (Extended Data Fig. 4). Note that all scores reported are the weighted accuracy based on the sampling rate of each class within the column.
The top level of the hierarchy (the object model), distinguished neurons from non-neurons as well as erroneous detections. The cross-validated accuracy score on the column was 96% with a test score of 97%. The second level of the model simply distinguished excitatory from inhibitory neurons. Here, the column cross-validated accuracy score was 94% and the test set was 93%. Overall, across all subclasses, the hierarchical model on the column had a cross-validated accuracy of 91% and a dataset-wide test set accuracy of 82%.
Chandelier cell identification
Chandelier cells are characterized by their unique axo-axonal synapses onto the AIS of target pyramidal cells. As there were no chandelier cells within the densely reconstructed column, we sought to test whether the perisomatic feature space would facilitate an enriched dataset-wide search for these cells. After identifying and proofreading a chandelier cell, we selected the top 20 nearest neighbours by Euclidean distance using a KDTree search of the perisomatic feature space (nucleus, soma and PSS features) after z-score normalization of each feature across cells. We also selected 20 random cells from the predicted inhibitory neurons. For each of these 40 cells, we proofread the reconstructions to ensure that there were no extraneous neurites attached, and extended the axon until there were at least 100 output synapses. On average, each of the 20 nearest neighbours had 590 output synapses attached and the random cells had 809 synapses attached.
To quantify whether a given cell was a chandelier or not, we measured the angle (ϕ) and the distance (r) between every output synapse and the soma of the postsynaptic cell (Fig. 6c). A synapse with an angle value of 0° would be considered to be directly above the target soma whereas one with an angle of 180° would be considered to be below it. Owing to variations in axon directionality with respect to the pial surface, we considered synapses with angle values between 160° and 180° and within 60 µm of the soma to be on the AIS of the target soma. In fact, because the specificity of chandelier targeting is so high, the density of synapse angle distributions alone was enough to identify other chandelier cells (Fig. 6e). On inspection of the proofread 20 nearest neighbours, we determined that cells with more than 40% of their synapses within 160–180° were chandelier cells. The average normalized density for the identified cells was 62% as compared to 8% for the non-chandelier cells. A two-tailed Fisher exact test was carried out to test significance between the random cell population and the nearest neighbours.
Inhibitory neuron output targeting
After characterizing a single 5P-NP-targeting cell, we applied a similar strategy to the one above to search for more neurons in the dataset that had a similar connectivity pattern. We selected the top 20 nearest neighbours by Euclidean distance in the perisomatic feature space using a KDTree search. These cells were proofread to remove false mergers and the axon was extended to include at least 100 synapses. It should be noted that there were five cells for which the axons could not be extended owing to volume boundaries or segmentation errors, so they were replaced with the five nearest cells. On average, each of the 20 nearest neighbours had 448 synapses attached.
To quantify whether a cell preferentially targeted 5P-NP neurons, we measured the fraction of total output that targeted different predicted subclasses. Cells that output more than 30% of their synapses onto 5P-NP cells were considered to have this rare connectivity preference. A two-tailed Fisher exact test was carried out to test significance between the random cell population and the nearest neighbours.
Predicted subclass densities
To measure the predicted cell densities per subclass across the MICrONS dataset, we divided the dataset into 50-µm2 bins in the x–z plane. For each bin, we calculated the number of cells in each subclass and scaled that value to the number per square millimetre to facilitate direct comparisons to reported densities in the literature.
Dataset 2
The second dataset covers a millimetre-square cross-sectional area, and 50 µm of depth within the primary visual cortex of a P49 male mouse18,20,51. The largest available segmentation spans layer 2/3 of the cortex through to layer 6. After applying the nuclear detection model18 and filtering out all nuclear objects below 25 µm3 and cells that were cut off by the volume border (see the section above entitled Filtering procedure), 1,944 cells were used for the analysis. The class type of each cell was labelled manually and used as the ground truth. Owing to the thinness of the volume, much of the distal cell morphologies were cut off and thus subclass type labelling was not possible. Nuclear and somatic mesh cleaning as well as feature extraction and normalization followed the same procedures outlined above.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.