Glacial isostatic adjustment reveals Mars’s interior viscosity structure

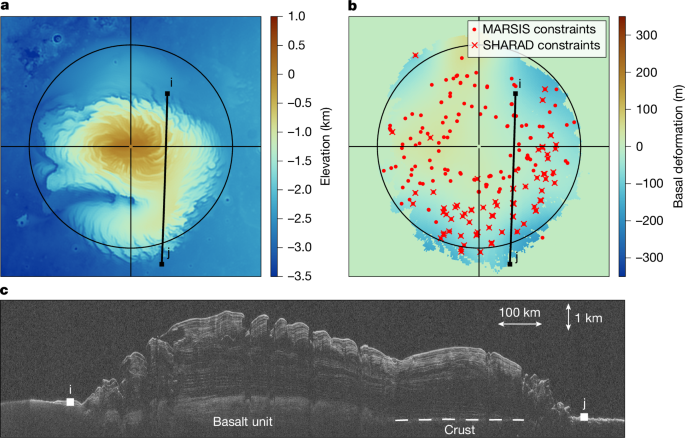
Constraints on the deformation beneath the north polar cap

The deformation beneath the north polar cap is obtained by comparing estimates on the polar cap thickness from elevation and radar data following ref. ⁶. In that work, the polar cap thickness was estimated by subtracting the observed ice cap elevation from a preloading surface constructed using elevation data far from the polar cap and unaffected by flexure (Extended Data Fig. 9). MARSIS radar analyses were performed at 213 locations spatially scattered across the polar deposits. All available MARSIS radargrams close to each location were investigated, and the reflections arising from the icy surface and the ice–substratum interface were visually identified. Using the same framework, analyses of SHARAD radargrams were performed at those 213 locations. Because of its higher frequency, SHARAD does not penetrate through the sand-rich basal unit and we here only retain locations where the ice–crust interface is observed (n = 78).

The radar thickness depends on the dielectric properties of the icy materials, which are not uniquely known for the entire north polar cap. On the other hand, viscoelastic deformations depend on both the interior structure and density of the loading materials. Therefore, we compare our simulated viscoelastic deformations to radar measurements using an r.m.s. misfit function for all interior models considering a real dielectric constant range of 2.5 to 3.5 and an ice density of 920 to 1,500 kg m⁻³ covering the possible presence of water and dry ice and dust in the ice cap^5,6. We limit our ice density and dielectric constant parameter space by considering possible mixtures of dust, water and dry ice using a three-component Maxwell–Garnett mixing model⁶. The density of water and dry ice is considered to be 920 and 1,560 kg m⁻³, respectively, and the dust density is assumed to range from 2,200 to 3,400 kg m⁻³. The dielectric constants of these same materials are 3.0, 2.5 and 6.0, respectively^5,6. Because of these, a model with an ice density of 920 kg m⁻³ (pure water ice), but with a dielectric constant of 3.5, can be safely ruled out as it does not correspond to any existing mixture of ice and dust in the north polar cap.

By accounting for uncertainties linked to the range resolution of MARSIS, surface roughness at the scale of the Fresnel zone of MARSIS and the uncertainty when estimating the preloading surface, an upper limit on the r.m.s. was estimated to be 266 m (ref. ⁶). Using the same approach and because of the higher frequency and resolution of SHARAD, a lower maximum allowed misfit of 175 m is given to the SHARAD comparison. Thus, a model is deemed acceptable if the r.m.s. misfit for MARSIS and SHARAD is no more than 266 and 175 m, respectively.

For context, Fig. 1b shows a flexure map beneath the north polar cap that was obtained by interpolating the radar-derived flexure using a 400-km moving window to obtain a smooth basement map and to get rid of short-wavelength uncertainty in elevation and radar-derived polar cap thickness. For comparison, a similar map using a dielectric constant of 2.75 instead of 3.0 is shown in Extended Data Fig. 9. In both cases, the present-day deformation beneath the north polar cap is no more than a few hundreds of metres.

Thermal evolution modelling

We have run 84 Martian 3D geodynamic models considering a wide range of parameters using the GAIA code^7,18,29. Therein, conservation equations of mass, linear momentum and thermal energy, are solved from 4.5 Ga to the present day given a set of model parameters. Key parameters that control the present-day thermal state of the interior are core radius, crustal thickness and radiogenic heat production, some of which have been recently constrained by InSight^7,25,30. Our geodynamic simulations use the 3D structure of the crust, as derived from gravity, topography and InSight data²⁶. Absolute viscosities can be obtained using the Arrhenius viscosity law and considering reference values for the viscosity, pressure and temperature⁷.

All tested models use the following naming convention: d_c^InSight − ρ_south(−ρ_north), where d_c^InSight is the crustal thickness at the InSight landing site in kilometres and ρ_north and ρ_south are the bulk density of the northern and southern hemisphere crust in grams per cubic centimetre (Extended Data Fig. 1 and Extended Data Table 1). If only one crustal density, ρ, is indicated, this value is assumed to be constant across the planet. If added, λ provides the crustal heat producing element enrichment factor with respect to the nominal Gamma Ray Spectrometer measured average (below). Models with additional annotations have higher activation energy (E = 325 kJ mol⁻¹), initial temperature (T_init = 1,850 K), temperature difference across the mantle (ΔT = 2,205 K) and have a η_jump 25-fold mantle viscosity jump compared to the reference values used in most other cases (that is, E = 300 kJ mol⁻¹, T_init = 1,650 K, ΔT = 2,000 K, no viscosity jump, see Extended Data Table 1 for further details). The effect of these parameters within their allowed possible ranges is minor compared to crustal thickness (Fig. 2).

In our nominal models, crustal heat production is laterally constant and equal to the surface average of 49 pW kg⁻¹, estimated from Gamma Ray Spectrometer data²⁸. However, because the spectrometer instrument is only sensitive to the first upper tens of centimetres of the surface⁴⁵, different composition and heat production may exist at greater depth. Therefore, we also consider models in which the bulk crust has a heat production different from the near surface, with an enrichment factor, λ, of 0.83 and up to 2. The upper bound leads to heat production of 98 pW kg⁻¹, which is slightly higher than the highest measured crustal heat production of 75 pW kg⁻¹ (ref. ²⁸), making it a reasonable upper range. Because the number of radiogenic elements in a planetary interior is finite, some models with a thick crust cannot reach crustal enrichment factors of 2, as the mantle is already fully depleted. Thus, our approach establishes an upper limit for Mars’s mantle viscosity (and the lowest possible temperature) within our geodynamic evolution framework. Whereas higher viscosities may be obtained using a higher reference viscosity, these models would be mostly conductive and be unable to explain ongoing volcanism on Mars.

Geologic observations and geophysical models indicate the presence of melts in the Martian interior^19,20,21. All of our models are able to predict melting at the present day when considering the present-day Martian solidus as estimated in ref. ⁴⁶. From our initial set of 84 geodynamic models, we select a subset of 27 end-member models with a wide range of viscosity structure for our viscoelastic analyses (Extended Data Table 1).

Thermal profile to lithosphere elastic thickness

A thermal profile can be converted to an elastic lithosphere by setting the bending moment of an elastic plate equal to that of the bending stresses in a more realistic rheology that considers fracturing and viscous flow⁴⁷ as

where the left term corresponds to the analytic integration of the bending moment of an elastic plate with thickness T_e, and in which ν is Poisson’s ratio, E_y is Young’s modulus and K is the lithosphere curvature. The right term computes the bending moment limited by the yielding strength of the lithosphere (\({\sigma }_{{\rm{YSE}}}\)), and where z is the depth, z_n the depth of the neutral plane and T_m is the mechanical thickness⁴⁷. The yield strength of the lithosphere strongly depends on temperature variations and includes faulting and viscous stresses. The mechanical thickness is defined as the depth where bounding stresses are close to zero, here approximated to 50 MPa (refs. ^5,47).

Thermal profiles from our interior models are converted to an equivalent elastic thickness using the TeHF code⁴⁸ that solves the above equation. We consider a wide range of model parameters including, a dry and wet diabase rheology for the crust, a dry and wet olivine rheology for the mantle. For each rheology, we consider strain rates of 10⁻¹⁷ to 10⁻²⁰ s⁻¹ consistent with the timescale of mantle convection and polar cap formation¹⁸ (Fig. 3). The curvature of the lithosphere is also varied from 10⁻⁹ to 10⁻¹¹ m⁻¹ (ref. ⁶). For all models, this conversion approach leads to elastic thicknesses less than 270 km, which is inconsistent with constraints from elastic flexure indicating elastic thicknesses more than 330 km (refs. ^5,6, Extended Data Fig. 1). This demonstrates that previous elastic modelling must be revisited to consider the interior transient viscoelastic response.

Calculation of viscoelastic deformation

The vertical displacement at time t_end, colatitude and longitude (θ,ϕ), are determined by the convolution of the spectral representation of the load potential change over the considered time interval with the transfer function represented by the load Love number h′ as

where g₀ is the gravitational acceleration at the surface, l and m are the degree and angular order, Y_lm are real spherical harmonics and l_max. is the maximum spherical harmonic degree used for calculations. The change in the load potential of the north polar cap (V_lm) is calculated assuming a mean bulk density ranging from 920 to 1,500 kg m⁻³ and using the polar cap thickness derived from elevation data and radar measurements^5,6. For simplicity and because of a lack of observational data, we solely increase the polar cap thickness over time, based on the current morphology of the north polar cap. We do not consider any radial expansion and growth.

Love numbers are computed based on the internal structures predicted by thermal models (Extended Data Fig. 2) using a Maxwell rheology and up to l_max. = 50, which is largely sufficient to resolve the polar cap loading (roughly degree 8, wavelength of 1,250 km). We show that the effect of using a transient rheology such as Andrade is minor compared to the uncertainty in mantle viscosity structure, and note that it does not change the time behaviour for the considered long-term process (Extended Data Fig. 10). The ALMA code assumes an incompressible interior. Compressibility affects Love number calculation, leading to slightly higher deformations. This effect is considered as second order when compared to the uncertainty in Mars’s interior structure.

Each interior model from our thermal evolution simulation is discretized into 68 constant-thickness layers with a given density, viscosity and rigidity, from the core to the surface. This number of layers is chosen to optimize the calculation of the load Love number using ALMA. The interior rigidity is computed using Perple_X (ref. ⁴⁹) together with the interior temperature, pressure and TAYAK mineralogy^7,26,27.

This study uses average one-dimensional interior profiles to constrain viscoelastic deformations beneath the north polar cap. Although future work may achieve larger accuracy by modelling 3D deformations from a 3D interior structure and polar cap load, several mitigating factors should be noted. Our 3D geodynamic models indicate that Mars’s northern regions show homogeneous properties (rigidity, viscosity, temperature) comparable to the global average (Extended Data Fig. 5). This indicates that lateral variations in the interior structure have minor effects on the estimated deformations. In particular, we expect these effects to be markedly lower than the current uncertainty in Mars’s interior structure (Fig. 2). Furthermore, the axisymmetric shape of the north polar cap load reduces the influence of the polar cap geometry on deformation estimates. For these reasons, differences between a full 3D viscoelastic loading model and our current model are expected to be small.

Polar cap loading history and past ice caps

On Mars, polar caps have grown and decayed following the planet’s obliquity cycles²³. It is not uniquely known how obliquity has varied in the planet’s recent history (500 million years ago), as orbital models become chaotic as one goes backward in time³³. Yet, it is generally thought that past polar caps existed in the geologically recent history^23,34, and these may affect the present-day deformation in the northern regions.

To model this process, we have constructed a loading history in which north polar caps grow and decay. Our first model starts at 430 Ma with no polar cap, and builds up a 3.2-km-thick polar cap in 5 Myr following a half cycle of a cosine function, removes that polar cap in 5 Myr and then repeats with a new cycle. The radius of the edge of the polar cap is constant. The interior response associated with the ice cap periodic growth and decay is modelled over the full process duration using the viscoelastic formalism described above. The two end-member viscosity structures from our ensemble of geodynamic models are tested with this time-loading history. In both cases, the flexure values at the present day are 35 and 45 m larger than when neglecting this past history for the low- and high-viscosity models, respectively (Extended Data Fig. 6).

We have also tested these same interior models against the ice-accumulation history of ref. ²³. This model starts at 10 Ma with a past north polar cap that disappears at about 8 Ma. After a time interval with no north polar cap, a new polar cap forms with a near linear increase in thickness from 4 Ma to the present day (Extended Data Fig. 7). A key unknown is what was the state of the 10 Ma ice cap and whether it was long-standing and at equilibrium or more recently formed. In one model, we assume that the previous ice cap was present over the last 500 Ma and thus at equilibrium (Extended Data Fig. 7) and in a second model, we assume that it formed at 14 Ma (Extended Data Fig. 8). In the case where the ice cap was long lasting, the present-day deformation increased by up to 70 m, whereas it only increased by a few metres for a young former ice cap.

The above tests show that the deformation beneath the north pole can only be increased when considering the effect of ancient ice caps. Whereas this effect would reduce our inferred maximum age for the polar cap by a few million years ago, it would not affect our constraints on Mars’s interior structure.

Constraints on polar deformation from time-variable gravity

Previous work inverted for Mars’s static and time-varying gravity field on the basis of tracking of Mars Global Surveyor, Mars Odyssey and Mars Reconnaissance Orbiter missions over 8 Martian years⁹. Here we build on that work by analysing residual trends in C₂₀ and C₃₀ after the zonal harmonics are corrected for seasonal variability. In both cases, the sign of these coefficients is negative, indicating the planet’s gravitational oblateness and north–south asymmetry. We correct the time-varying signal of these zonal harmonics for annual, semi-annual and tri-annual variations, as well as half (5.5 years) and full solar cycle periods (11 years, ref. ⁹). The function used to fit the both C₂₀ and C₃₀ time-variable coefficients is in the form of

where P₁ to P₁₀ are the best-fit periodic coefficients, t is time in seconds past J2000, T₁ = 365 × 86,400 × 1.880894, T₂ = 365 × 86,400 × 0.940447, T₃ = 365 × 86,400 × 0.626965, T₄ = 11 × 86,400 × 365 and T₅ = 11 × 86,400 × 365/2.

After this correction, the residuals show trends with slopes of 1.5 ± 1.6 × 10⁻¹⁸ and 2.5 ± 3.3 × 10⁻¹⁹ s⁻¹ for the C₂₀ and C₃₀ coefficients, respectively (Extended Data Fig. 4 and Extended Data Table 2). Given the negative sign of C₂₀ and C₃₀, positive trends suggest polar ice accumulation and that the south polar cap is accumulating less ice compared to the north polar cap. For those time-variable coefficients the Pearson correlation coefficients (r values) are 0.13 and 0.06, respectively. We further test the null hypothesis that the residuals have no correlation with time using Wald’s test. For the C₂₀ and C₃₀ coefficient residuals, we obtain P values of 0.35 and 0.46, respectively, which are both higher than typical significance levels of 0.05. Together, these values indicate a positive slope, although not statistically significant.

After 1 Martian year, our analysis indicates a \(\Delta {C}_{20}\) value of 4.7 × 10⁻¹¹ and \(\Delta {C}_{30}\) of 7.7 × 10⁻¹². Together, these can be used to derive the north polar gravitational acceleration as

where G is the gravitational constant, M and R are Mars’s mass and radius. Based on this equation, our measured \(\Delta {C}_{20}\) and \(\Delta {C}_{30}\) imply north polar gravitational acceleration of 6.4 × 10⁻⁵ mGal. Using the Bouguer plate formula, 2πGρh, and a water ice density of 920 kg m⁻³, the above gravity acceleration suggests a maximum ice-accumulation rate of 1 mm per year when not accounting for isostatic adjustment. This value is consistent with predicted rates of 0.50 to 1.06 mm per year by climate models^23,39, indicating that gravity residuals provide information on north polar processes.

Our models predict that glacial isostatic adjustment is ongoing, with downward deformation rates of 10⁻⁴ to 4 mm per year (Fig. 3). In our framework, glacial isostatic adjustment pushes the mantle downward such that the gravitational signature of this process should be scaled by mantle density (3,500 kg m⁻³) and has an effect opposite to ongoing ice accumulation that scales with water ice density (920 kg m⁻³). Given the overall purity of the north polar layered deposits⁵, dust accumulation is not accounted for here. Erosion rates that have been measured to be small, 2 × 10⁻⁴ mm per year (ref. ⁵⁰), are also neglected. Owing to its higher elevation, the south polar cap is expected to only accumulate small amount of dry ice⁵¹, which is here neglected.

Because of a lack of a clear trend in our residual gravity analyses, we here assume that the gravitational potential from ongoing subsidence cannot be higher than from the polar cap accumulation rate. This indicates that ongoing subsidence rates must be at most around 26% (920/3,500) that of ice accumulation. Ice-accumulation estimates from previous work therefore limit the subsidence rate to less than 0.13 mm per year (ref. ³⁹) or less than 0.28 mm per year (ref. ²³) and we here use the minimum of these two values to limit our parameter space (Fig. 3). Choosing the other value has no effect on our derived viscosity structure, but would provide a lower limit to the polar cap age of 0.9 Ma instead of 1.7 Ma.

Moment rate inversion from InSight

The InSight seismometer has detected dozens of marsquakes over its 4 years of activity²⁴, but none from the north polar regions (75–90° N). Analyses of InSight data have shown that a 3.8 to 3.9 magnitude event originating from these northern regions could have been detected¹⁰. Because the seismic moment rate depends on the strain rate experienced by the seismically competent lithosphere^40,41, it is possible to invert for a maximum strain rate in the northern regions based on this non-observation. The maximum strain rate is obtained by comparing the seismic moment rate \(({\dot{M}}_{{\rm{seismic}}})\), as measured by InSight, to a geodetic moment rate \(({\dot{M}}_{{\rm{geodetic}}})\) obtained from the Kostrov equation⁴⁰.

Mars’s seismic moment rate based on the InSight catalogue can be defined in terms of the b value¹⁰ as

where n is the number of terrestrial years, M_g is the magnitude of the seismic event and Γ is the gamma function. The geodetic moment rate, which depends on the strain rate originating from lithospheric deformation, \(\dot{\varepsilon }\), scales as

In this equation, α is a seismic efficiency factor ranging from 0 to 1, V is the seismogenic volume and μ is the average shear modulus throughout this volume.

Given the non-observation of 3.9 magnitude marsquakes at high latitudes over the 4-year lifetime of the InSight mission, substituting \({\dot{M}}_{{\rm{geodetic}}}\) and \({\dot{M}}_{{\rm{seismic}}}\) in the above equations can be used to infer a maximum strain rate as a function of α, μ and V. The shear modulus μ is obtained from the interior models and the seismogenic volume V is calculated assuming a seismogenic depth given by the 573 or 1,073 K mantle isotherms⁵². In our models, μ and V are found to range from 44–72 GPa and 67–334 km, with a low shear modulus corresponding to models with a thin seismogenic layer thickness. The seismic efficiency factor, α, however, is mostly unknown for Mars, although it has been shown to be less than 0.7 (ref. ¹⁰). As a result, we consider this parameter to be 0.7 or 0.03, the latter of which is the minimum value that has been estimated on Earth⁴¹.

We derive the maximum strain rate from the non-observation of marsquakes in the northern regions over 4 years of InSight data collection to be 1.84 × 10⁻¹⁸ s⁻¹. As shown in Fig. 3, young polar caps (less than 1 Ma) show strain rates that are higher and inconsistent with the InSight-derived moment rate, and these models are thus excluded.