Continued Atlantic overturning circulation even under climate extremes

Models and experiments

We analyse the AMOC upwelling pathways in 34 CMIP6 models (Extended Data Table 1) from the pre-industrial control (piControl) simulation⁵¹ and their responses under two extreme-forcing scenarios: the ‘abrupt-4xCO2’ experiment⁵¹ (‘4xCO2’ herein) and the ‘u03_hos’ experiment from the North Atlantic Hosing Model Intercomparison Project¹⁹ (NAHosMIP). In 4xCO2, atmospheric CO₂ concentrations are instantaneously quadrupled from piControl levels and maintained for 150 years. In u03_hos, a uniform freshwater forcing of 0.3 Sv is applied to the North Atlantic between 50° N and the Bering Strait for at least 100 years. We examine seven CMIP6 models in u03_hos. We use a single ensemble member from each run (Extended Data Table 1). All available models are included in our analysis to ensure a wide range in the AMOC’s upwelling pathways, enabling robust relationships to be inferred.

Variables

We analyse the monthly mean overturning mass streamfunction, including both Eulerian mean and parameterized eddy components³⁴, in depth space (variables, ‘msftmz’ or ‘msftyz’) and in density space (variables, ‘msftmrho’ or ‘msftyrho’), in six models that provide this variable or in which we calculate it. We average the overturning streamfunction over the first 50 years of the piControl simulation, and over the 20-year period centred on 90 years into the 4xCO2 and u03_hos experiments to obtain the ‘future’ state. We focus on the period 90 years in the extreme-forcing experiments because it is available in all models and because the AMOC has generally stabilized. We calculate the AMOC strength (where AMOC is defined as the Atlantic Ocean mid-depth overturning cell) from the maximum Atlantic streamfunction value north of the Equator and below 500 m depth. We calculate the PMOC strength from the maximum Indo-Pacific streamfunction value at 34.5° S, between 500 m and 4,000 m depth, to exclude wind-driven gyres and unrelated deep overturning circulations. Although weak PMOC cells are present in the control experiment of a few models (Fig. 3a,c), they are confined to the deep ocean and thus do not affect the magnitude of the AMOC’s upwelling pathways. In density space, the AMOC and PMOC strengths are defined similarly to those in depth space, but at a neutral density greater than 1,026 kg m⁻³ in the HadGEM3 models and at a density referenced to 2,000 m greater than 1,035 kg m⁻³ in 4 other models analysed (Extended Data Fig. 4).

Calculating the AMOC’s upwelling pathways

Upwelling pathway definitions

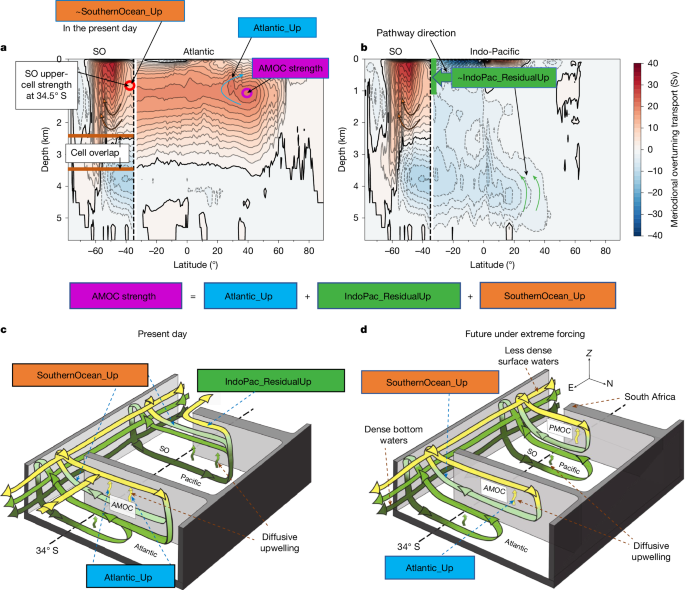
We apply the method of ref. ³, adapted from ref. ³⁷, to calculate the AMOC’s upwelling pathways (Fig. 1a). These pathways quantify the time-mean area-integrated volume transports that return deep waters from the AMOC’s southwards branch to its shallower northwards branch (Fig. 1c). We define the AMOC strength as its maximum strength below 500 m depth in the North Atlantic (Fig. 1a, purple circle). The upwelling pathways—Atlantic (‘Atlantic_Up’), Indo-Pacific residual (‘IndoPac_ResidualUp’) and SO (‘SouthernOcean_Up’)—define the regions where AMOC origin waters upwell before rejoining the northwards branch of the AMOC. Each upwelling pathway is greater than or equal to zero and collectively match the AMOC strength (equation (4) and Fig. 1) as the global overturning circulation conserves volume.

We determine the three upwelling pathways by analysing the zonally integrated meridional overturning streamfunction in the Atlantic and Indo-Pacific oceans, and a globally integrated streamfunction in the SO, defined as latitudes south of 34.5° S (Fig. 1). These have units of sverdrups (10⁶ m³ s⁻¹). The Atlantic upwelling pathway (Atlantic_Up, blue box) corresponds to the upwelling rate of AMOC deep waters in the Atlantic Ocean that return northwards nearer the surface, inferred from the closed streamlines of the AMOC (Fig. 1a). The SO upwelling pathway (SouthernOcean_Up, orange box) quantifies total upwelling of North Atlantic (that is, AMOC) origin waters by the SO upper cell, including those that first upwell in the Indo-Pacific (Fig. 1). The Indo-Pacific residual upwelling pathway (IndoPac_ResidualUp, green box in Fig. 1b) quantifies the AMOC’s upwelling pathway in the Indo-Pacific Ocean that does not later upwell in the SO (the latter is accounted for by SouthernOcean_Up). Upwelling of AMOC origin waters in the South Indo-Pacific Ocean subtropical gyre cells that first upwell in the SO (most notable in CESM2-based models) are also accounted for by SouthernOcean_Up, not IndoPac_ResidualUp. We calculate the Indo-Pacific residual upwelling pathway as a residual using equation (4), which ensures volume conservation in the ocean.

In ref. ³, we showed that in a transient state, changes in AMOC strength are balanced by changes in the AMOC’s upwelling pathways, and vice versa. These changes are communicated rapidly by non-advective wave processes³¹, ensuring a global upwelling–downwelling balance to conserve volume. Thus, on a decadal or longer timescale, the time-mean AMOC upwelling pathways are equal to the time-mean AMOC strength (Fig. 2). Changes in the meridional overturning circulation remote from, but connected to, the North Atlantic through the overturning streamfunction therefore modulate the AMOC strength, even if the AMOC weakening is instigated by changes in North Atlantic forcing.

Equations

The equations used to calculate the upwelling pathways (equations (1)–(4)) are:

where AMOC_max is the maximum AMOC strength north of the Equator (referred to as the AMOC strength in the main text; purple circle in Fig. 1a), AMOC_min (≥0 Sv) is the minimum value among the maximum AMOC strengths simulated at each latitude, calculated between 34.5° S and the Equator (grey circle in Extended Data Fig. 10), AMOC_34S is the maximum AMOC strength at 34.5° S, PMOC∣_{z_AMOC_34S} is the PMOC strength (≥0 Sv) at 34.5° S at the depth of AMOC_34S, and ψ_max∣_{ϕ = 34.5°S} is the maximum (at any depth) of the globally integrated SO upper cell strength at 34.5° S (red circle in Fig. 1a).

South Atlantic and Indo-Pacific overturning cells

In some models, a weak, localized South Atlantic circulation at 34.5° S, isolated from the North Atlantic, upwells in the SO (Extended Data Fig. 10). This circulation, denoted ‘South_Atlantic_local’ (equation (2) and Extended Data Fig. 10), is accounted for when calculating both the Atlantic upwelling pathway (equation (1)) and the SO upwelling pathway (equation (3)) as it reduces SO upwelling (that is, the globally integrated SO upper cell strength at 34.5° S, ψ_max∣_{ϕ = 34.5°S} (red circle in Fig. 1a)) available for upwelling AMOC deep waters. ‘South_Atlantic_local’, determined from equation (2), is reduced if a component of the localized South Atlantic waters enters an anticlockwise overturning cell in the Indo-Pacific Ocean, upwells and rejoins the northwards branch of the localized South Atlantic circulation. This is because these waters do not upwell in the SO and thus do not reduce SouthernOcean_Up.

Under extreme forcing, most models develop a PMOC that upwells in the SO, further reducing the amount of SO upwelling available to upwell AMOC deep waters. We therefore modify the method of ref. ³ to account for the presence of a PMOC. A latitudinally expansive PMOC at the depth of the AMOC maximum at 34.5° S, z_AMOC_34S, indicates that any AMOC waters that enter and upwell in the Indo-Pacific Ocean must later upwell in the SO to rejoin the AMOC’s northwards branch, as they cannot bypass the PMOC. This scenario occurs in the future state of all models with a PMOC (Extended Data Figs. 2 and 3), ensuring that IndoPac_ResidualUp is zero (Fig. 2d,h). If SouthernOcean_Up, calculated from the first expression on the right-hand side of equation (3), exceeds the AMOC transport into the SO (AMOC_min; grey circle in Extended Data Fig. 10), we adjust SouthernOcean_Up to match AMOC_min (second expression on the right-hand side of equation (3)). This ensures that the AMOC’s SO upwelling pathway is not stronger than the AMOC transport into the SO, as required by conservation of volume. We therefore implicitly account for the impact of the PMOC on the AMOC’s SO upwelling pathway in this case, based on conservation of volume. We account for the PMOC implicitly rather than explicitly to prevent inaccuracies in the upwelling pathways that would otherwise occur in the following scenarios.

1. 1.

   If the PMOC maximum is below z_AMOC_34S, then AMOC deep waters can enter the PMOC’s northwards branch before upwelling in the SO (most notable in CESM2-based models).

2. 2.

   If a localized clockwise overturning cell at 34.5° S is present in the upper Pacific Ocean (found in the control state of a few models; for example, Extended Data Fig. 1f,g), then SO upper cell waters enter the northwards near-surface branch of these Pacific cells, sink and later enter the AMOC’s northwards branch via SO zonal transports.

In these scenarios, not all the southwards PMOC transport at 34.5° S reduces the AMOC’s SO upwelling pathway (SouthernOcean_Up), so explicitly accounting for the maximum PMOC strength at 34.5° S would underestimate this upwelling pathway.

We therefore only explicitly account for upwelling of PMOC deep waters in the SO if they cannot be connected to the AMOC (first expression on the right-hand side of equation (3)), unlike in the scenarios above. Thus, we subtract the PMOC strength at the depth of the maximum AMOC strength at 34.5° S, z_AMOC_34S, from ψ_max∣_{ϕ = 34.5°S} when calculating SouthernOcean_Up (equation (3)). Hence, if the PMOC maximum is shallower (deeper) than z_AMOC_34S, we subtract the magnitude of the southwards (northwards) PMOC transport below (above) z_AMOC_34S to calculate SouthernOcean_Up. This results in a small decrease in SouthernOcean_Up during the initial 30 years of the forcing experiments relative to not explicitly accounting for these PMOC transports.

Our approach is validated by IndoPac_ResidualUp tending rapidly (over several decades) towards zero (Fig. 2d,h) before we constrain it to zero by setting SouthernOcean_Up to AMOC_min (second expression on the right-hand side of equation (3)). The PMOC rapidly expands, preventing upwelling above the PMOC’s base. Therefore, IndoPac_ResidualUp quickly tends to zero when a PMOC forms. Our approach is further validated by the strong correlation between the inverse future PMOC strength and the change in the AMOC’s SO upwelling pathway (Fig. 4a,c), despite our approach not explicitly accounting for the PMOC in the future-state calculations (when SouthernOcean_Up is set to AMOC_min). The outlying CESM2-based models in Fig. 4c,f and Fig. 5b,d (purple shading) emphasize the importance of implicitly accounting for the PMOC in the future state to prevent inaccuracies in the magnitude of SouthernOcean_Up (see scenario 1 above). We further validated our method by examining the overturning streamfunctions across models and experiments for inconsistencies with their calculated upwelling pathways.

Southern Ocean buoyancy fluxes

Following ref. ⁵², we calculate the surface buoyancy flux, B, across 16 CMIP6 models using equation (5):

where g is the acceleration due to gravity, ρ₀ is the reference density of seawater and S₀ is the reference salinity. The net surface heat (Q_H; W m⁻²) and freshwater (Q_F; kg m⁻² s⁻¹) fluxes are positive for surface ocean inputs of heat and freshwater, respectively. We allow the thermal expansion and saline contraction coefficients (α and β) to vary with latitude and time, using the sea surface temperature and salinity variables (‘tos’ and ‘sos’, respectively) from each model. The net surface heat and freshwater flux variables (‘hfds’ and ‘wfo’, respectively) include contributions from sea-ice fluxes. We separate the heat and freshwater fluxes into their components—the net longwave and shortwave radiation (‘rls’ and ‘rss’), latent and sensible heat fluxes (‘hfls’ and ‘hfss’), precipitation and evaporation fluxes (‘pr’ and ‘evspsbl’), and sea-ice freshwater fluxes that are calculated as a residual. We calculate the multi-model mean components from a subset of nine models that provide all these variables (Extended Data Fig. 7b). We find that using a time-varying thermal expansion coefficient causes large shifts in the changes in the heat flux components, but these shifts mostly compensate each other, resulting in only minor differences in the net surface heat and buoyancy flux changes (a slight reduction in the maximum positive changes). Therefore, we show changes in the heat flux components using the thermal expansion coefficient from the control simulation (Extended Data Fig. 7b) to accurately determine the cause of the net buoyancy flux changes.

Significance tests

We conduct a two-tailed Student’s t-test to assess significance of correlations between variables. A P value below 0.05 is considered significant, indicating a 95% confidence level.