A travelling-wave strategy for plant–fungal trade

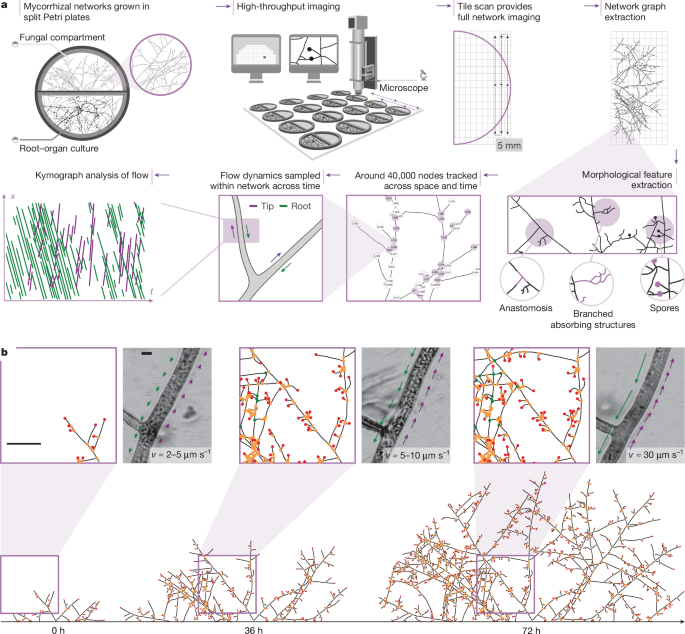
Biological material and plate preparation

We performed experiments with Ri T-DNA transformed carrot root (D. carota clone DCI) organ cultures colonized by R. irregularis strain A5 (DAOM664344), R. irregularis strain C2 (DAOM664346)⁵⁶ (I. Sanders) and R. aggregatum. We cultivated fungal stocks on modified Strullu–Romand (MSR) medium^57,58 in association with transformed carrot root for 2–6 months until plates were fully colonized. We then used these stock cultures to inoculate sterile roots, as described below.

Each biological sample contained a root-organ culture in a split Petri plate (94 mm diameter, Greiner Bio-One). One side contained the root colonized with AM fungi, and the other side contained a fungus-only compartment. We designed trapezoid shaped acrylic frames to fit against the central barrier of the two-compartment split plates. These 1-mm-thick frames had a longer top edge (88 mm) than bottom edge (85.5 cm), and a consistent height (12 mm). The frames included a central opening (50 × 2 mm) that was located 2 mm from the top edge. This opening connected to the upper edge of the central barrier of the plate and was covered by a nylon mesh, leaving only a 50-mm-wide window for the fungus (but not the root) to cross through into the second compartment. A nylon mesh (pore size, 50 μm, 9 × 71 mm) was attached to the acrylic frame using UV resin such that the frame opening was fully covered by the mesh and free of resin. The resin was cured with UV light for 3 min. The frames were then wrapped in aluminium foil and sterilized at 80 °C for 72 h.

We filled the two compartments with MSR medium. In the fungus-only compartment, we used regular MSR (per 1 l, 739 mg MgSO₄·7H₂O, 76 mg KNO₃, 65 mg KCl, 4.1 mg KH₂PO₄, 359 mg Ca(NO₃)₂·4H₂O, 0.9 mg calcium pantothenate, 1 mg biotin, 1 mg nicotinic acid, 0.9 mg pyridoxine, 0.4 mg cyanocobalamin, 3 mg glycine, 50 mg myo-inositol, 1.6 mg NaFeEDTA, 2.45 mg MnSO₄·4H₂O, 0.28 mg ZnSO₄·7H₂O, 1.85 mg H₃BO₃, 0.22 mg CuSo4₄·5H₂O, 2.4 mg Na₂MoO₄·2H₂O, 34 mg (NH₄)Mo₇O₂₄·4H₂O). In the root compartment, the phosphate content of the medium was reduced to 1% (that is, 1%P MSR) of the abovementioned concentration (41 mg l⁻¹ KH₂PO₄). We supplemented all media with 10 g l⁻¹ sucrose and 3 g l⁻¹ Phytagel. We verified that the addition of sucrose to the fungal compartment did not change the dynamics discussed in this Article (Extended Data Fig. 8). In the plates where carbon availability was doubled, the sucrose concentration in the media in the root compartment was increased to 20 g l⁻¹ sucrose.

In a laminar airflow hood, we filled one compartment of a sterile two-compartment split plate with 28 ml MSR medium. We placed an autoclaved sheet of cellophane (Hoefer TE73, semi-circle with trapezoidal overhang at the straight edge) on top of the solidified medium. We then folded the cellophane overhang into the empty second compartment. We next inserted the custom acrylic frame into the empty compartment, securing the cellophane overhang between the acrylic frame, central barrier and the bottom of the plate. To avoid dislocation of cellophane and/or frame, we poured 5 ml 1%P MSR into the second compartment to immobilize the components. We then filled the compartment to a total of 25 ml 1%P MSR.

To quantify the saturation density and internal flow velocities of AM fungi in the absence of host roots, we used MSR medium with 0.3% (w/v) Phytagel as a growth substrate. For the myristate treatment, we supplied the medium with 0.5 mM myristic acid (Sigma-Aldrich; stock concentration 0.5 M in acetone). The control treatment lacking myristate (0 mM) received the same volume of acetone. After autoclaving, we filled 15 ml of medium in small Petri dishes (60 mm). Once fully cooled, we placed a circular sterile piece of porous cellophane (Hoefer TE73, 50 mm) onto the surface of the medium. The 0.5 mM concentration of myristic acid (C₁₄H₂₈O₂) contributed a total of 1.3 mg of carbon to the 15 ml of medium in the plate, which was then inoculated with spores as described below.

Inoculation of fungal material on root system

In a laminar airflow hood, we transferred 2–3 cm of in vitro Ri T-DNA transformed D. carota root (genotype 1 or 2) to the root compartment of the split plate. This compartment was not covered by cellophane. We then cut a circular plug containing only AM fungal mycelium and spores from fungal stock plates. We placed the inoculation plug on top of the root, covering around half of the root. We sealed the plates with parafilm and stored them horizontally and upright in an incubator at 25 °C. For AM fungi grown with myristate, we inoculated the centre of each plate with 10–15 spores in mixture of single spores and clusters without roots. In all cases, we checked plates regularly for growth and removed any roots crossing from the root compartment into the cellophane-covered fungal compartment. The AM fungi colonized the roots in roughly 30 days, crossing into the fungus-only compartment around 5–6 weeks after inoculation. For AM fungi grown without roots, we used a similar time frame (around 2 months). We recorded the time of the first barrier-crossing event, which was set as time zero, after which we began imaging network formation.

Image processing

Details of image processing describing the segmentation of hyphal segments and spores as well as network graph extraction and node tracking can be found in Supplementary Methods.

Analysis

Defining network features

Defining the ROI. To detect and describe all network features, we first defined the ROI for analysis within the fully stitched image of the fungal compartment. To avoid border effects, we defined the ROI as the area between a line that ran parallel to the central barrier of the split plate, separated by 6 mm from the barrier, and a 4.5 cm radius semicircle centred at the midpoint of that line within the plate.

Classifying graph edges into BASs and RH. We considered that a given edge of the network graph belonged to a BAS when any of these three criteria were met: (1) the length of the edge was less than 400 μm; (2) the length of the edge was less than 1,000 μm and one of the two end points of the edge coincided with the end point of a hypha (that is, a tip); (3) the average width of the edge was less than 7 μm and the product between this width and the length was less than 9,000 μm². These choices were inspired by the definition of BASs according to a previous study³³, with parameters tuned to achieve satisfactory BAS detection under visual evaluation. Edges that did not belong to a BAS were designated as belonging to an RH. The total length of RH shown in Fig. 4b is therefore the total length of all edges of the network minus the total length of BAS edges.

Width estimates for BAS identification. Although the low (×2) magnification used for network extraction does preclude accurate determination of hyphal width, we found that, to discriminate between RH and BAS, it was helpful to use crude width estimates obtained using the following procedure. First, transects perpendicular to the hyphal edge and of 120 pixels in extent were generated using the function profile_line of the package skimage⁵⁹. We then fitted a Gaussian function to the resulting curve using the curve_fit function of the scipy.optimize⁶⁰ package. Width was defined as two times the s.d.

Growing tip definition. Growing tips were defined as tracked nodes of degree 1 that were at least 40 pixels from their detected position in the last image frame where they were detected. Most network tips (degree 1 nodes) are non-growing BAS tips. Imperfect network alignment or extraction sometimes led to artefactual detection of growth in non-growing tips, which meant a non-zero speed was not a sufficiently robust criterion for detecting actively growing tips. It was therefore important to analyse non-growing BAS tips separately (see below).

Classifying growing tips into BAS and RH. Although the classification criteria for graph edges based on hyphal filament dimensions (see above) were sufficient for accurate estimation of total RH and BAS lengths, they did yield a finite rate of classification errors that tended to be higher near growing tips (because edges near RH tips had similar dimensions to BAS edges). Those errors had little effect on total length estimation but did significantly affect the estimation of growing tip density. Accurate estimation of growing tip density therefore required distinct classification criteria from those of edges. A growing tip was therefore designated as belonging to a RH if its final position was at a distance greater than a threshold distance, 2.5 mm, away from its initial position and all other growing tips were designated as belonging to BAS. The threshold was set by visually assessing the classification quality. As the model described the population of RH tips, we chose to plot in Figs. 2 and 3 the density of growing RH tips. Including all growing tips did not affect the travelling-wave dynamics discussed in the text.

Detecting anastomosis (tip annihilation) events in space and time. Anastomosis events occur when growing tips fuse with hyphal edges to create junctions across which cytoplasm is connected. Thus, every anastomosis event is also a tip annihilation event that contributes to regulating colony growth and densification behind the advancing wavefront. To compute the anastomosis rate plotted in Fig. 3, we first detected anastomosis events in our tracking analysis, where they were defined as the subset of all events at which a tracked node’s degree jumps from 1 to 3, whose degree never reverts back to degree 1 thereafter. The complementary subset whose degree does revert back to 1 were classified as hyphal crossing events. We recorded for each anastomosis event its position in space, defined by the pixel at which the skeletonized T-junction trifurcates, and its time, defined as the last timestep in which they were of degree 1. The anastomosis rate (in units mm⁻² h⁻¹) within a given ring at time t was computed by dividing the number of anastomosis events occurring within that ring over a time interval [t,t + Δt] by the area of that ring and also by Δt, the time interval between two successive frames. For the total anastomosis count (Fig. 4), the method was adjusted to study the evolving topology of the network (see the ‘Total anastomosis count’ section).

Detecting branching events/newborn tips. Newborn tips, which result from branching events, at each timestep t were defined as growing tips that appeared for the first time at t. To compute the branching rate plotted in Fig. 3, we first detected branching events in our tracking analysis. The branching rate (in units mm⁻² h⁻¹) within a given ring at time t was computed by dividing the number of branching events occurring within that ring over a time interval [t,t + Δt] by the area of that ring and also by Δt, the time interval between two successive frames.

Distance from origin and travelling-wave speed. We defined the distance from origin r by approximating the polygonal convex hull of the colony as a semicircle, and computing from the convex hull area A the semicircle radius r as \(r=\sqrt{\frac{2A}{\pi }}\). The accuracy of this approximation for r is limited by the degree to which the convex hull of the colony is well approximated as a semicircle and varied across sample plates given the considerable random variation in colony shape. Inaccuracies in the estimate for r in turn leads to inaccuracies in the wave speed v estimated from the density profiles n(r) and ρ(r) at different times. For this reason, the growth speed of the ‘puller hyphae’ at the growing front v_p provides a more robust proxy for the travelling-wave speed, and was used to study the stability of wave speeds in Fig. 2 and Extended Data Figs. 1, 3, 4 and 8.

Definition of ‘puller hyphae’ at the growth front. At every timepoint t, we defined puller hyphae as those hyphae whose tip satisfies the definition for growing tips (see above), and in addition resides at the growth front at time t. Tips were defined to be at the growth front at timestep t if they were a vertex of the colony’s convex hull at both timesteps t and t + 1.

Definition of the time coordinate. In Figs. 2d, 3d and 5, zero on the time axis corresponds to the start time of imaging, which was initiated as soon as crossing into the fungal compartment was detected by manual examination of the pre-imaging sample pool. As those manual examinations were carried out once every 2 days, on average, the zero point on these time axes is therefore later than the actual crossing time by an unknown interval of up to 2 days. To compare temporal network development across samples in Fig. 4b–e, it was necessary to align in time the data from each sample. We therefore defined the offset time t* as the time at which the total RH length in the fungal compartment reached 100 mm, and plotted data from all samples as a function of t − t*.

Definition of the arrival time t_n at the nth ring. The arrival time t_n (used as a time offset in Fig. 2c) at which the travelling wave passes through the nth ring was defined as the time at which the front of density within that ring reached half of its maximal value. To obtain t_n for the hyphal density wave, we fit a sigmoid curve of equation \(\rho (t)={K}_{1}\frac{1}{1+{{\rm{e}}}^{\lambda ({t}_{n}-t)}}\) to the hyphal density timeseries in the nth ring, with K₁, λ and t_n as free parameters. For the tip density wave, we fit the curve of equation \(n(t)={K}_{2}\frac{{{\rm{e}}}^{\lambda ({t}_{n}^{{\prime} }-t)}}{(1+{{\rm{e}}}^{\lambda ({t}_{n}^{{\prime} }-t)}{)}^{2}}\) with K₂, λ and \({t}_{n}^{{\prime} }\) as free parameters.

Total anastomosis count. Whereas spatially resolved detection of anastomosis events for Fig. 3 achieved through tracking (see above) allowed us to estimate the rate of tip annihilation after formation of three-way nodes, the aim of the total anastomosis count across the entire network (Fig. 4) was to study the evolving topology of the network. As described in the Supplementary Methods, a fraction of anastomoses also occurred at crossing points (that is, degree 4 nodes), which do not lead to tip annihilation but might significantly affect the overall graph topology. We therefore used a different technique to detect anastomoses for the total-count analysis, based on graph theory. According to Euler’s formula for planar graphs, there is a relationship between the number of faces (which equals the number of anastomoses), the number of nodes v and the number of edges e and the number of faces f: v − e + f = 2. The number of edges and number of nodes were readily accessible from the extracted network graph. We found through high-magnification control experiments (Supplementary Methods) that around 10% of all anastomoses computed through the Euler formula corresponded to anastomoses at degree 4 nodes. Counting or not counting them does not substantially affect the overall picture, but we nevertheless included them in the anastomosis count (Fig. 4c).

Analysis of flows

Kymograph generation

We recorded transport videos at high magnification (×100), as described in Supplementary Methods. We captured more than 1,600 videos at 20 or 25 fps for a minimum duration of 20 s across a total of 28 biological samples (split Petri plates). Within each biological sample, we recorded videos at different positions within the network (between 20 and 100 distinct positions per plate). We captured all videos within RH. We sampled flows as a function of spatial position across the network and this was done in a manner that follows particular hyphae (>90% of videos), as exemplified by the experiment shown in Fig. 5d. As these bright-field videos are label free, they effectively integrate information about the motion of any organelle or other biological object within the cytoplasm that produces sufficient intensity contrast. Most videos exhibited simultaneous antiparallel flows of such contrast objects (Supplementary Video 5), with some directed towards the host, that is, the root (Fig. 5a (green arrow)) and others toward the tip of the hypha (Fig. 5a (purple arrow)). For kymograph analysis, we analysed each video by first picking a linear (one-pixel wide) ROI of length 20 µm (Fig. 5a (white arrow)) at the centre of a straight section of the hypha to obtain at every image frame a (one-dimensional) vector of pixels x. We then arrayed x at each image frame to obtain a 2D image (kymograph) where one axis (shown vertically, in the example of Fig. 5a) represents the spatial dimension along x (of total length 20 µm) and the other axis (Fig. 5a (horizontal)) represents time (over the entire duration of the video, ranging from 20 s to 60 s). Example kymographs are shown in Extended Data Fig. 10, including kymographs from networks grown without a host in myristate (Extended Data Fig. 10). Given the label-free nature of the imaging performed, these kymographs represent a superimposition of many trajectories of individual contrast objects within the cytoplasm (detected generically as ‘particles’ in our speed analysis; see below) as their position along x evolves from frame to frame.

Speed extraction

We extracted one kymograph with multiple trajectories per video recorded, that is, a total of more than 1,600 kymographs to sample around 100,000 trajectories across a range of positions in space and times throughout network development. The kymograph extraction was done using MATLAB. We detected from each kymograph a set of individual trajectories by using a deep learning software for automated kymograph analysis (KymoButler, Wolfram Mathematica) developed previously⁴⁹. This program works by using a fully convolutional deep neural network to identify bidirectional tracks to obtain from each kymograph a collection of particle trajectories. We imposed a minimum duration of ten consecutive frames as a constraint on the trajectory detection algorithm to ensure that detected trajectories correspond to the actual motion of contrast objects. Very short trajectories (below 500 ms in duration) could be associated with tracking errors across image frames that give rise to erroneous (and often anomalously high) flow speeds being detected. Imposing this constraint led to robust detection of correct flow speeds up to a limit of 40 or 50 µm s⁻¹ (for videos recorded at 20 or 25 fps, respectively), corresponding to the speed of an object that travels the full spatial extent of the kymograph (20 µm) in 10 image frames. We checked all kymographs manually after the automatic detection to validate our protocol and confirm the accuracy of our detected speeds. Example kymographs are represented in Extended Data Fig. 10. As seen in Extended Data Fig. 10, detected trajectories demonstrated movements in both directions (toward the tip in purple and toward the root in green) for around 3,600 trajectories per biological sample). The statistics of their average velocities are represented in the violin plots of Fig. 5b.

Maximum-speed extraction

As the automatic detection of average velocities did not capture outliers (that is, very rapid flows larger than 40–50 µm s⁻¹, mentioned above), we performed a manual screening of all recorded videos (more than 1,600 in number) to detect the fastest flow in each direction for each video. Once the fastest flows were identified within each video, the maximum velocity within the video was obtained by manually pointing at the slope of the corresponding trajectory (straight line) within the associated kymograph. We then obtained maximum velocities for each video as represented in Fig. 5c.

Over the entire set of over 1,600 videos investigated, only 7% of the videos (<120 in number) included maximum-speed outliers that were not detected automatically by the algorithm. This relatively low incidence of undetected outliers provided additional confidence that the average speed statistics represented from the automated detection (Fig. 5b) are reliably representative.

Spatial mapping within the network

We next mapped the spatial position of each flow video to the skeletonized network to enable analyses of flow velocities as a function of space, as seen in Fig. 5d–f. We recorded the acquisition x–y coordinate within the sample plate for each high-magnification flow video (using a ×100 objective, image size of 141 µm × 103 µm at the sample plane), and we aligned the full set of these coordinates for each plate with the network skeleton (extracted from the stitched image of the fungal compartment obtained with a ×2 objective) leading to a rough overlap. This first alignment was achieved by matching the x–y coordinates of one particular video (such as an easily identifiable tip) within the skeleton. We then manually performed a finer adjustment of the position of each video within the network by comparing the exact shape of each hypha imaged with the skeleton. The maximum error for alignment was around 100 µm (of the same order of magnitude as the size of the high-magnification field of view).

Distance to the tip

The distance to the tip corresponds to the curvilinear length to the tip of the hypha to which a given video position belongs—not the closest tip including other hypha of the network. A hypha is an equivalence class on the set of edges based on the continuity relationship. In brief, two edges belong to the same hypha if they are the trace left by the same growing tip. In practice hyphae can be recognized by a continuity in edge directionality and width at each junction. On the basis of visual identification, we manually defined which hypha each edge in a given video belonged to and therefore with which tip of the hypha it was associated. Distances are defined by the curvilinear length along the graph through the shortest path that goes from the video position to the tip.

Plate harvesting and DNA extraction

The roots were harvested from the split plate using tweezers, removing any trace amounts of media at 1 (n = 3), 3 (n = 5), 7 (n = 3), 12 (n = 4) and 30 (n = 8) days after R. irregularis A5 crossed to the fungal compartment. The total wet weight of the roots was measured and split for DNA extraction and root staining to determine colonization. The roots separated for DNA extraction were placed to dry in an oven in a paper bag at 80 °C and the dry weight was measured after 72 h.

The samples were first ground using liquid nitrogen and a mortar and pestle to disrupt the cells. DNA was extracted using the Qiagen DNeasy PowerSoil kit according to manufacturer’s instructions. One change was made in the duration of the first centrifugation step, lengthened from 30 s to 3 min to better separate the supernatant. DNA was eluted into 50 µl 10 nM Tris-HCl, pH 8.5, and quantified using the Nanodrop Spectrophotometer ND-1000. For phosphorus content determination of roots and agar, see the Supplementary Methods.

Intraradical mycelium quantification

To quantify intraradical length, we used two methods: (1) one traditional method relying on root staining and visual quantification (that is, the Trouvelot method)⁶¹; and (2) one method using droplet digital PCR (ddPCR)^62,63 to calculate the number of nuclei and then convert it to length of hyphae based on our calculated nuclear density per µm of hyphae (Supplementary Methods). We used ddPCR with fluorescent probes specific to AM fungi, targeting sequences that occur only once per nucleus (that is, the single-copy MAT gene) to directly quantify the total number of nuclei across the hyphae⁶⁴. For each plate, four non-template controls and four positive controls (R. irregularis, A5 DNA extracted from pure culture) were used to set the fluorescence amplitude threshold (high threshold) values to distinguish between the positive and negative droplet cloud. Once thresholds were set, we used the concentration (copies per µl) to calculate the length of hyphae using a modified formula from⁶³. To calculate the length of the hyphae in the roots (µm), this final value was then multiplied by the average distance between nuclei as described in the Supplementary Methods, Extended Data Fig. 6 and Supplementary Video 8.

Statistics and reproducibility

Network analyses

For Fig. 3b and Extended Data Fig. 12e–g, ring-frame temporal profiles were computed over n_ring = 15 rings, sampled across the same growing network.

For Fig. 3c, speed histograms were computed from n_pink = 1,645 and n_cyan = 103 growing tips.

For Extended Data Figs. 1b, 3b, 4b and 8b, datapoints represent the mean over the n growing tips at the front observed at each timepoint. The value of n fluctuated in the range 1 ≤ n ≤ 21, with 77% of all timepoints in the range n ≥ 3.

For Extended Data Fig. 2, the number of samples for each data series is given by p/t/n where p is the panel label, t indicates genotype and/or treatment, and n is the number of independent biological replicates: a/A5-100C/10, a/A5-200C/2, a/C2-100C/5 a/C2-200C/3, a/Agg-100C/4, b/AMF/23, b/free-living/25, c/A5-100C/20, c/A5-200C/13, c/C2-100C/11 c/C2-200C/12, d/A5-100C/10, d/A5-200C/2, d/C2-100C/5 d/C2-200C/3, e/genotype-1/22, e/genotype-2/6, f/genotype-1/27f/genotype-2/18, h/symbiotic/23, h/myristate/5.

Extended Data Figure 11a was computed from 118 hyphal growth trajectories, and Extended Data Fig. 11b was computed from 71 RH and 881 BAS branch points, all sampled from the same growing network.

Flow analyses

For Fig. 1b, we observed speeds between 2 and 5 μm s⁻¹ in 43 videos acquired within the time interval t = 0.5–1.5 days, speeds between 5 and 10 μm s⁻¹ in 26 videos acquired within t = 1.5–2.5 days and speeds between 15 and 45 μm s⁻¹ in 8 videos acquired within t = 2.5–3.5 days.

For Fig. 5b, each pair of violin plots in the top panel (for positive and negative velocities) and points in the bottom panel (for the absolute ratio of positive and negative means) appearing at the same x coordinate corresponds to data from an independent biological replicate. The number of samples for violins at each x coordinate is given by x/p/r/k, where x is the timepoint (in days) at which that biological replicate was measured (x coordinate), p is the count of trajectories in the tipward direction, r is the count of trajectories in the rootward direction and k is the number of videos from that replicate: 0.4/464/494/12, 0.6/989/387/29, 1.4/527/516/13, 1.5/306/555/7, 2.3/774/941/22, 2.4/686/1,092/19, 3.3/402/872/23, 3.3/969/1,160/24, 3.4/1,678/1,060/54, 3.4/1,553/2,332/50, 4.4/592/1,084/24, 4.4/673/865/18, 4.6/1,475/1,842/52, 8.4/4,959/4,594/158, 10.6/677/614/22, 12.4/1,817/1,823/22, 13.3/825/1,546/16, 14.4/517/1,365/13, 15.3/1,223/1,284/22, 16.4/1,034/987/26, 17.5/2,468/1,373/53, 20.4/2,689/2,342/73, 21.4/9,595/8,414/284. In total, about 75,000 trajectories from approximately 1,200 videos were used.

For Fig. 5c, each pair of violin plots (for positive and negative extreme velocities) appearing at the same x coordinate corresponds to data from an independent biological replicate, except at x = 0, where 11 biological replicates had the same measured value along the x coordinate. The number of samples for violins at each x coordinate is given by x/p/r/k, where x is the number of spores measured at that x coordinate, p is the count of trajectories in the tipward direction, r is the count of trajectories in the rootward direction and k is the number of videos from that replicate: 0/8,060/9,026/309, 15/1,475/1,842/58, 38/1,223/1,284/32, 39/517/1,365/21, 60/1,553/2,332/55, 67/1,034/987/31, 72/2,494/2,437/54, 73/4,959/4,594/177, 84/825/15,46/27, 249/9,595/8,414/332, 380/2,689/2,342/81, 857/2,468/1,373/59 In total, about 1,200 videos were used. For each video, only the maximum value of all trajectories is used for the violin plot.

For Fig. 5e, each pair of violin plots (for positive and negative velocities) appearing at the same x coordinate corresponds to data from one kymograph, from a set of videos sampled across network locations indicated in Fig. 5d. The number of samples for each violin is given by x/p/r, where x is the distance to the tip (x coordinate), p is the count of trajectories in the tipward direction and r is the count of trajectories in the rootward direction: 0.01/3/2, 1.02/1/0, 1.73/1/0, 2.31/2/1, 2.79/1/0, 3.78/1/29, 3.78/1/29, 3.78/1/29, 3.78/1/29, 6.33/1/43, 6.33/1/7, 6.33/60/43, 6.33/60/7, 6.87/64/35, 6.87/4/35, 7.85/0/4, 8.64/5/10, 9.22/48/94, 9.22/48/36, 9.22/5/94, 9.22/5/36, 12.0/4/43, 12.0/4/14, 12.0/35/43, 12.0/35/14, 12.72/24/74, 12.72/24/29, 12.72/45/74, 12.72/45/29, 14.57/21/40, 14.57/14/35, 14.57/14/40, 14.57/21/35, 14.94/2/44, 14.94/2/24, 14.94/4/44, 14.94/4/24, 17.19/40/32, 17.19/50/32, 17.19/50/32, 17.19/40/32, 17.89/23/46, 17.89/27/39, 17.89/27/46, 17.89/23/39, 20.53/2/79. In total, 824 trajectories from 27 kymographs were used. Each violin corresponds to one video.

For Fig. 5f, each pair of violin plots (for positive and negative velocities) appearing at the same x coordinate corresponds to data from one kymograph, from a set of videos sampled across network locations indicated in Fig. 5d. The number of samples for each violin is given by x/p/r, where x is the BC (x coordinate), p is the count of trajectories in the tipward direction and r is the count of trajectories in the rootward direction: 0.01/1/0, 0.01/3/2, 0.06/1/0, 0.07/1/0, 0.07/2/1, 0.08/1/29, 0.08/1/29, 0.08/1/29, 0.08/1/29, 0.09/64/35, 0.09/4/35, 0.18/0/4, 0.21/60/43, 0.21/60/7, 0.21/1/43, 0.21/1/7, 0.21/5/10, 0.25/5/94, 0.25/5/36, 0.25/48/94, 0.25/48/36, 0.37/4/43, 0.37/4/14, 0.37/35/43, 0.37/35/14, 0.42/40/32, 0.42/50/32, 0.42/40/32, 0.42/50/32, 0.43/2/79, 0.47/24/74, 0.47/24/29, 0.47/45/74, 0.47/45/29, 0.5/23/46, 0.5/27/39, 0.5/27/46, 0.5/23/39, 0.58/14/35, 0.58/14/40, 0.58/21/35, 0.58/21/40, 0.6/2/44, 0.6/2/24, 0.6/4/44, 0.6/4/24. In total, 824 trajectories from 27 kymographs were used. Each violin corresponds to one video.

For Fig. 5b–f, all violin plots plotted using violinplot function of matplotlib Python library with the parameter show_extrema set to false. All linear fits computed using regplot function of seaborn Python package⁶⁵. It computes the regression line and shows a 95% confidence interval as a shaded area around this regression line.

For Extended Data Fig. 7c, for all box plots, the number n of independent biological replicates was n = 7.

For Extended Data Fig. 10g, violin plots were constructed from n trajectories from p videos sampled across k independent biological replicates. For networks connected to host roots n = 71,009, p = 113, k = 11; for networks in non-symbiotic context n = 2,450, p = 86, k = 7. We excluded immotile objects, which we defined as trajectories demonstrating displacements indistinguishable from diffusion, demonstrating speeds below a threshold of 0.8 μm s⁻¹ corresponding to the average speed of a one pixel wide (r = 35 nm) particle diffusing for Δt = 20 s (video length) in water (\(D=\frac{{k}_{b}T}{6\pi \eta r},v=\sqrt{\frac{D}{\Delta t}}\)). This lead to excluding about 50% of the trajectories in the case of myristate, where flows were generally less active.

Intraradical colonization imaging

For Extended Data Fig. 6b–f, imaging with DAPI staining was done on three independent plates on three different days showing similar results.

Bootstrap resampling uncertainties

For Fig. 2b, we obtained uncertainty estimates for hyphal and growing tip density by splitting each ring in which densities were computed into a set of 10,000 rectangles of equal area, computing the densities in each of the rectangular area separately, and estimating the s.d. of the mean density by bootstrap resampling (sampling with replacement) 100 times over the set of rectangular area densities. The shaded regions correspond to two times the s.d. of the bootstrap resampling.

For Extended Data Figs. 1a, 3a, 4a and 8a, as the bootstrapping procedure used for Fig. 2c is computationally costly, for these Extended Data figures on replicates we estimated uncertainties in the density by assuming scaling relations based on relative magnitudes of uncertainties in Fig. 2b. Specifically, we used σ_ρ = 160 μm mm⁻² × ρ/ρ_sat for the filament-density uncertainty and σ_n = n/4 for the tip-density uncertainty. The shaded regions correspond to the mean ± σ_ρ,n.

For Fig. 2c,d, the shaded region is the confidence interval obtained by bootstrap resampling 1,000 times the sigmoid fit of each density profile in each ring reference frame. A function \(\rho (t)={K}_{1}\frac{1}{1+{{\rm{e}}}^{\lambda ({t}_{n}-t)}}\) was fitted to the resampled hyphal density timeseries in the n-th ring, with K₁, λ and t_n as free parameters. The grey region in Fig. 2c,d shows, respectively, the interval around the mean value of K₁, t_n ± 2 times the standard error of the bootstrap estimates of these parameters.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.