Interplay of geometrical and spin chiralities in 3D twisted magnetic ribbons

Multiphoton lithography

To fabricate the 3D twisted ribbons, a super-resolution STED microscope (Abberior Instruments) was adapted extensively in both hardware and software, to perform MPL. A functional diagram of the system is shown in Supplementary Fig. 1. A femtosecond Er fibre laser (Menlo Systems C-Fiber 780) is used to generate multiphoton excitation at an 80-MHz repetition rate and at a wavelength of 780 nm. The optical pulse power is controlled by an acousto-optic modulator before focusing the beam onto a liquid photoresist through a Nikon Plan Apo Lambda 100×/1.45 Oil objective lens. Precise motions of the objective along the optical axis (z-axis) are controlled by the combination of a motorized focus stage embedded in the microscope (Nikon Ti-2, working distance: 10 mm) and an XYZ piezostage (Physik Instrumente P-545.3C8S PInano, working distances: 200 μm for all axes). XY-motions are achieved by the combination of an XYZ piezostage and a coarse motion stage (Physik Instrumente U-780 PILine XY-stage: working distances: 135 mm (x-axis) and 85 mm (y-axis)). The coarse motion stage allows for the fabrication of large structures such as contact pads.

The fabrication process is as follows: first, one drop of photoresist is applied onto a borosilicate glass coverslip that is placed on the microscope sample stage. The glass–photoresist interface is automatically positioned by monitoring the reflection from the substrate surface using a photodiode. The interface positioning errors are less than 200 nm. To improve adhesion, the fabrication is started by focusing the laser inside the substrate. During the fabrication, the laser is scanned along the xy-axes using a set of galvano scanners (maximum scanning range of 80 μm) and along the z-axis using an XYZ piezostage. The photoresist used for fabrication is composed of 7-diethylamino-3-thenoyl-coumarin (DETC, Luxottica Exciton) as the photoinitiator, 0.25 wt% concentration, and pentaerythritol triacrylate (PETA, Merck Sigma-Aldrich) as the monomer. The photoresist is prepared by precisely weighing each component chemical and mixing them with a magnetic stirrer for 20–40 min at room temperature until the photoinitiator is observed to be completely dissolved in the monomer. This type of photoresist has been widely used and characterized in previous experiments with STED-MPL³⁷. Laser excitation pulses with 0.2 nJ energy are applied at an 80 MHz repetition rate. The laser is XY-scanned at a speed of 6.25 mm s⁻¹ with the galvano scanner. To reduce the surface roughness, the scanning step interval is set to be 25 nm along the x- and z-axes. After the illumination, the unpolymerized photoresist is removed by submerging the sample in propylene glycol monomethyl ether acetate (PEGMEA, Merck Sigma-Aldrich) for 25 min, followed by submersion in 2-propanol for 5 min. Finally, the sample is carefully dried with dust-free compressed air to avoid residue or dust on the surface.

Film growth 

After the MPL process is completed, the glass substrate is cut into smaller pieces in preparation for deposition. The magnetic film stacks are deposited onto both the polymer structures and glass substrate by magnetron sputtering at an Ar pressure of 10⁻³ torr at room temperature. The deposition system has a base pressure better than 10⁻⁹ Torr. The film growth rates are about 0.9 Å s⁻¹ for Pt and about 0.2 Å s⁻¹ for FM and Ru films. A 100 Å thick TaN layer is first deposited to improve the adhesion and the smoothness of the following films. TaN capping layers, 30 Å and 60 Å thick, are used to prevent the oxidation of the magnetic layers for the SAF and FM films, respectively. Full film stacks are 100 TaN/30 Pt/3 Co/7 Ni/3 Co/60 TaN and 100 TaN/30 Pt/3 Co/7 Ni/1.5 Co/9.5 Ru/3.5 Co/7 Ni/3 Co/30 TaN for FM and SAF films, respectively (all thicknesses are in Å). Although the sputtered beams are not highly directional or collimated, no films are deposited on the substrate surfaces that are shadowed by the suspended sections of the fabricated structure. By contrast, as the substrate is rotated during deposition, the grown films are mostly uniform over the flat and twisted regions in the ribbons.

Atomic force microscopy

An Asylum Research Cypher atomic force microscope is used to check the roughness of the deposited films. The suspended region of the 3D device with a +11° twist together with a contiguous section of the substrate is scanned along the ribbon direction in tapping (a.c.) mode to minimize the perturbations at the ribbon edges. The pixel size was set to 10 nm with a scan rate of 0.3 Hz and a voltage of 600 mV. The values given in the paper correspond to the root mean square of roughness, R_q. The measured R_q is about 0.37 nm in the twisted region with ζ = +11° (as compared with the approximately 0.1 nm RMS roughness for the substrate itself) (Supplementary Note 4).

Kerr microscopy

Current-induced DW motion on the 3D twisted magnetic ribbon structures is measured using polar Kerr microscopy at room temperature (Fig. 1c and Supplementary Fig. 2). The polarizer in the Kerr microscope linearly polarizes the incident light. By contrast, a λ/4 waveplate is combined with an analyser to measure the Kerr ellipticity, allowing the magnetization contrast along the z-axis to be detected. Devices are wire-bonded by contact pads. The device resistances are measured before and after characterization to probe for notable changes in the devices such as deformations from Joule heating, with variations typically less than 1%. A nanosecond pulse generator is used to move the DWs. The rise and fall times of the voltage pulses are 0.3 ns and 0.8 ns, respectively. Pulse lengths longer than 10 ns are typically applied unless DW nucleation is observed. Sometimes 8 ns long pulses are used when higher voltage pulses are needed for the experiment and 10 ns pulses are observed to promote nucleation (owing to heating effects).

First, a DW is nucleated at either end of the ribbon by fields or current pulses, or a combination of both. Then the DW is driven into the twisted region by sequences of current pulses. Differential mode Kerr microscopy is used: an initial image is used as the background that is subtracted from the image being acquired after a sequence of current pulses has been applied. This process significantly improves the magnetic contrast and resolution of images by minimizing the effect of drift and vibrations on the Kerr contrast. Consequently, the processed Kerr image shows two boundaries in the ribbon that correspond to the previous and present DW positions. These complete process cycles (DW nucleation and motion) are automatized and repeated three to five times to check the reproducibility and for statistics. The current pulse length is limited to avoid Joule heating of the ribbons that are poorly thermally connected to the surface.

The upper bound of J is limited by DW nucleation, whereas the lower bound corresponds to J_c below which the speed of the DW is less than 5 m s⁻¹. In each measurement cycle, a DW is attempted to be driven along the whole ribbon by applying a sequence of current pulses. Each Kerr image is acquired after the application of current pulses, corresponding to the DW displacement during the pulses (Fig. 2). A sequence of current pulses with a minimum pulse length t_p = 10 ns is typically applied between each Kerr image acquisition. Pulses that are 7 ns and 30–50 ns long are used for higher and lower J, respectively, as the larger t_p often heats the suspended 3D structures that are rather poorly thermally connected to the substrate. This also limits the maximum J, by more than 40% compared with the counterparts on Si substrates, that can be applied and, thereby, the maximum DW velocity. A 10 ns long pulse is typically used, although 7 ns and 30–50 ns long pulses are used for higher and lower J, respectively. Each cycle is repeated thrice to check reproducibility. As for the magnetic ribbon with ζ = −45°, the sample is placed on a wedge at 22.5° angle to enhance the Kerr image contrast.

Data processing

A semi-automatic classification algorithm is developed to locate DW positions from the acquired images. First, a denoising process is applied to each image during the acquisition cycle by image reconstruction using a multistage progressive image restoration³⁸. After denoising, the ribbon edges are automatically detected, after which the reconstructed images are normalized, and the contours of the magnetization shade are detected and filtered based on the area and aspect ratio. The resulting contour candidates are presented to the user for selection. The DW positions are determined from the boundaries of selected contours, from which the velocity is calculated based on the input parameters, such as pulse lengths. The average velocity along the ribbon is obtained from the initial and final positions of the DWs for each measurement cycle and the corresponding number of applied pulses.

Vibrating sample magnetometry

The magnetic properties of unpatterned films are characterized by measuring the easy-axis (out-of-plane) and hard-axis (in-plane) loops with a vibrating sample magnetometer (Lakeshore VSM 8600) at room temperature. The applied field range is ±20 kOe (easy axis for SAF films and hard axis) and ±2 kOe (easy axis for FM films). Both FM and SAF films show excellent perpendicular magnetic anisotropy. The SAF films exhibit large AF exchange coupling and a small net magnetization (see Supplementary Note 5 for magnetic properties, including magnetic hysteresis loops, magnetizations, anisotropies and symmetric and antisymmetric exchange interactions).

Cross-sectional transmission electron microscopy

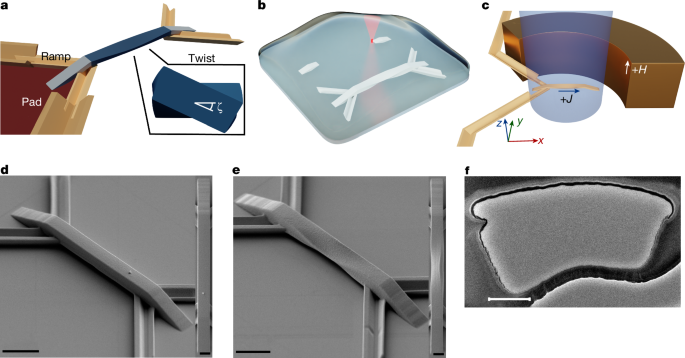
The uniformity of the film deposition through a cross-section of a device was characterized for a device with ζ = −11° through transmission electron microscopy (TEM). The TEM sample preparation was performed using a TESCAN GAIA3 FIB-SEM workstation. First, the suspended sections of the devices were coated with protective layers of C and Pt using focused electron and ion (Ga) beam-induced deposition, Then, a small slice of the device cross-section in the middle of the suspended section was cut for each device, attached to a Cu TEM-grid and gradually polished with decreasing beam current. A final, low-energy polishing step was performed to clean the exposed surfaces from implanted Ga ions. During the electron-beam-induced deposition, the suspended section of the device was seen to deform, leading to the surface curvature and indentation noticeable on the left side of Fig. 1f, but the deformation did not influence the characterization outcome as the film thickness over the polymer scaffold was unaffected and the sliced cross-sections were not further modified during the remainder of the process. High-resolution TEM characterization of the processed cross-section was performed using a JEOL JEM-F200 microscope, at 200 kV. Cross-sectional TEM on the region with ζ = +11° shows that the deposited films are uniform and conformally grow on the scaffold surface except near the edges of the ribbon in which the films are thinner with a thickness gradient (Fig. 1f). No film was found to be deposited onto the shadowed areas or the backside of the suspended ribbon. The thinner regions at the ribbon edges may cause DW pinning during current-induced motion.

3D twisted magnetic ribbons with different chiral twists

A 3D device is composed of three sections: two ramps, a suspended ribbon, electrical contact leads and a pad delimitation structure (Fig. 1a,b). The ramps not only support the suspended ribbon but also allow for electrical access from contact pads to the suspended ribbon. The suspended ribbon has a twisted region along the longitudinal direction with two different chiral twists at opposite ends of the ribbon so that both ends are horizontal with respect to the ground plane. For example, one half of the twisted region has a left-handed geometrical chirality (−), whereas the other half has a right-handed geometrical chirality (+). V-shaped structures with a 90° cross-section angle are prepared by MPL to electrically isolate the two electrical contact leads to the device. These structures are used to eliminate additional processing that would otherwise be needed. Suspended ribbons were fabricated that are 20 μm long and 1.25 μm, 2.5 μm and 5 μm wide, with ζ = 0, ±11°, ±18°, ±26° and ±45°. The 2.5-μm wide ribbons were chosen for detailed measurements. Each ramp has a 10-μm projected length on the ground plane with an elevation angle of 18° for all devices. We define the section within each half of the ribbon that has a constant twist parameter as having an effective twisting length L ≈ 4 μm. The twist parameter ξ is defined as ξ = ζ/L such that the twisting angle X along the twisting axis x, is given by X = ξx (see Supplementary Note 2 for more details).

The fabricated twisted ribbons have two distinct regions: the ribbon is twisted over one half of its length with one-handedness (region A) and then twisted with the opposite-handedness over the second half (region B), as shown in Extended Data Fig. 2. This enables the ramp structures to be identical at either end of the ribbon (Methods). To investigate the current-driven DW motion in the 3D twisted ribbons with two opposite chiralities, the DW displacements for low and intermediate J in Fig. 2c,d are replotted in Extended Data Fig. 2. The data show that the twisting of the ribbon significantly influences the DW motion and strongly depends on the DW configuration, whether \(\odot \)⊗ or ⊗\(\odot \). For J ≈ 1 × 10⁸ A cm⁻² (Extended Data Fig. 2a), the ⊗\(\odot \) DWs are blocked in region A for the 3D twisted ribbon with ζ = +11° (region A, left half) and −11° (region B, right half). By contrast, \(\odot \)⊗ DWs pass through region A but are stuck in region B (ζ = −11°), as shown in Extended Data Fig. 2a. By contrast, for the twisted ribbon having ζ = −11° (region A, left half) and +11° (region B, right half) and vice versa (Extended Data Fig. 2c). An example for an intermediate value of J is shown in Extended Data Fig. 2b,d.

Geometrical chiral-twist-dependent local exchange energy

To illustrate how the local exchange energy E_ex is affected by the chiral twist, schematic illustrations are shown in Fig. 4. The arrows on the 3D twisted ribbons represent the local magnetizations M. that is, red: \(\odot \) (up domain) and blue: \(\otimes \) (down domain) and green: DW. Here we consider the untilted DW case (χ = 0) only, for simplicity. Note that 3D twisted ribbons have two distinct faces, upper and lower, as the 3D twisted ribbons are mathematically orientable (but a Möbius strip is not orientable, that is, it has only one face). Figure 4a,b shows how the orthogonal unit vector set \(\{\hat{{\bf{p}}},\hat{{\bf{r}}},\hat{{\bf{u}}}\}\) (thick black arrows) at the edge of the 3D twisted ribbon rotates around as the ribbon gets twisted by ζ = −180° (left-handed chirality) or ζ = +180° (right-handed chirality). The orientation of M can be defined with respect to either the upper or the lower face. Here the upper face at the left end of the ribbon (that is, x = 0) has been chosen to define the orientation of M. For example, the \(\odot \)⊗ DW configuration corresponds to θ = 0 (\(\odot \)) and π (\(\otimes \)) that are defined with respect to the normal vector \(\hat{{\bf{u}}}\) on the upper face when the domains are at the left end.

As the ribbon gets twisted by π, the upper face faces up at the left end of the ribbon, rotates around and then faces down at the right end of the ribbon. Importantly, although M does not rotate at all, a DW can be created just by twisting the ribbon if the DW width (πΔ) equals the twisting length (π/ξ) by a π-rotation, as shown in Fig. 4a,b. In this case, M rotates in the opposite direction as the ribbon twists around its length direction \(\hat{{\bf{p}}}\), such that M within the DW rotates less than the case without any twist, that is, the gradient of M becomes smaller. If the DW width were perfectly identical to the length of the π-twisted region, then \(\hat{{\bf{m}}}\) would be perfectly uniform within the DW, thus effectively equivalent to a single magnetic domain in the cartesian coordinate system while there are two domains with a DW in the curvilinear coordinate system. Note that the exchange energy is determined by the magnetization gradient in the cartesian coordinate system. This happens when the DW is a Bloch-type wall with either (1) ψ = π/2 and the ribbon twists around in the right-handed way (ζ > 0) or (2) ψ = 3π/2 and the ribbon twists around in the left-handed way (ζ < 0). This describes the case that M remains the same when the arrow colour changes in Fig. 4a,b. In these cases, the local exchange energy per unit volume ϵ_ex is small and is the same as that for a single domain in a flat strip as the gradient of M is zero.

By contrast, if M rotates in the same direction as the ribbon is twisted around, M has to rotate around twice, that is, 2π to form a DW as the ribbon gets twisted by π. This happens when the DW is a Bloch-type wall either having (1) ψ = 3π/2 and the ribbon twists around in the right-handed way (ζ > 0), or (2) ψ = π/2 and the ribbon twists around in the left-handed way (ζ < 0). In these cases, ϵ_ex is large as the gradient of M is large. These show that ϵ_ex is determined by the geometrical chirality of the 3D twisted ribbon and the chirality of the Bloch-type walls. By contrast, for the untilted Néel-type walls (ψ = 0 or π), ϵ_ex in the DW is not affected by twisting the ribbon, thereby equaling that for a DW in a flat strip as M in DW rotates in the direction orthogonal to what the ribbon twisted around. In this case, ϵ_ex is intermediate between the two cases above.

Combining all the cases above, we can readily find that an effective DMI field H_tor is induced by the interplay between the chiral twist and the helical Bloch-type wall chirality. The orientation of H_tor is determined by the DW configuration, and the sign of ζ such that the torsional torque τ_tor = −γM × H_tor results in a geometrical chirality and DW-configuration-dependent DW motion by current as observed in our experiments. Note, for clarification, that the interface DMI stabilizes a chiral Néel-type DW structure but the geometrical twisting favours a chiral Bloch-type wall when the DW is untilted. Thus, the actual structure of the moving DW lies somewhere in between.

Note that the above cases describe only untilted DWs for which case a DW has a tilting angle χ = 0. When χ ≠ 0, the situation becomes more complicated, and the details are discussed in Supplementary Note 2. A comprehensive summary of all the cases is presented in Extended Data Table 1.

Effective interface and twist-induced Dzyaloshinskii–Moriya interaction fields

The effective interface-induced DMI fields H_DM≈1 kOe are extracted by fitting the v–H_x curves shown in Extended Data Fig. 8a from which we find D = M_sH_DMΔ ≈ 0.52 erg cm⁻² (see Supplementary Note 5 for details). The twist-induced effective field H_tor = A_ex/(bM_sΔ) ≈ 126 Oe is obtained from A_ex = 34 pJ m⁻¹, M_s = 520 emu cm⁻³, Δ = 4 nm, L = 1 μm, ζ = 11° and ξ = ζ/L = 0.19 μm⁻¹. Note that H_tor plays a key part in the chiral-twist-dependent current-driven DW motion. From these, we find that the effective curvilinear chiral-geometry-induced DMI constant D_tor = 2ξA_ex = 6.5 × 10⁻³ erg cm⁻². Here, M_s is experimentally measured, whereas the value of A_ex is estimated by interpolation from literature values⁴⁰ for Co (56 pJ m⁻¹) and Ni (15 pJ m⁻¹) and the film stacks (3 Å Co/7 Å Ni/3 Å Co). By contrast, the value of ζ that is used is the nominally designed value, whereas the values of Δ and L are obtained by fitting v–J curves in Fig. 3. The fitted Δ = 4 nm is different from what is estimated (10 nm) from A_ex and K_eff above. Note that there are significant uncertainties in the determination of Δ. Δ =4 nm agrees with those from similar published film stacks that show Δ = 4.3 nm for 30 Pt/3 Co/7 Ni/1.5 Co (ref. ⁴¹). The fitted L = 1 μm is lower than the designed value L ≈ 5 μm (Supplementary Fig. 14). This difference may be because of the following. First, the effective L may be smaller than the designed L because the gradient of angle variation along the 3D twisted ribbon can deviate from linearity, as shown in Supplementary Fig. 14. Second, the fabricated structures are slightly off from the designed ideal 3D twisted ribbons apart from the nonlinear twisting angle variation. Third, our analytical model has been developed using approximations based on ξw ≫ 1 (where w is the width of the 3D twisted ribbon) for simplicity to capture the underlying physics, as discussed in detail in Supplementary Note 2. Fourth, hidden imperfections or pinning sites may amplify the chiral-twist-dependent current-driven DW motion. Larger geometrical chirality-induced DW motion in experiment than that in model predictions have also been observed in curved wires¹⁹ and Y-shaped wires²⁰ on flat surfaces. Most importantly, note that all trends of chiral-twist-dependent CIDWM agree well with the model predictions although there are quantitative differences between the experiment and the analytical model.

Torsional fields and torsional torques

We developed an analytical model to understand our observations. A comprehensive discussion is included in Supplementary Note 2.

Current-driven chiral DW motion with reversed DW chirality and/or opposite SHE-induced SOT in twisted ribbons

Our model shows that the twisting effect on the current-induced DW motion is determined not only by the geometrical chiral twist but also by the chirality of a Néel-type DW. To verify this prediction experimentally, we prepared twisted ribbons that are coated with two distinct film stacks that have reversed DW chirality and/or opposite SHE-induced SOT by placing a thick Pt layer on top of Pt/Co/Ni/Co and tuning the respective thicknesses of the Co and Pt layers¹⁸. We find that the measured current-induced DW motions in devices with reversed DW chirality and/or opposite SOT are significantly slowed down because of competition between the bottom and top interface DMIs and SOTs apart from the velocity reduction in 3D twisted ribbons compared with flat strips. This makes these experiments highly challenging for reliable measurements of DW motions that are much more susceptible to DW pinning–depinning at the greater number of imperfections in the 3D twisted ribbons. We find that the twisting effect can be masked by this DW pinning–depinning, as discussed below.

Note that the chirality of a Néel-type DW is determined by the competition between the DMIs induced from the bottom and top interfaces. When the DMI at the bottom Pt/Co interface is larger than that at the top Co/Pt interface, the DW is left-handed and when it is smaller, the DW is right-handed. The DMI strength is typically proportional to the Co layer thickness. By contrast, the SHE-induced SOT is positive when the SHE from the bottom Pt layer is larger and negative when the SHE from the bottom Pt layer is smaller than that from the top Pt layer. The SHE is proportional to the Pt layer thickness when the Pt layer is not much thicker than the spin diffusion length of Pt. Note that the film stack used in Figs. 2–4 has a left-handed DW chirality and a positive SHE-induced SOT.

First, the following film stacks were grown on flat Si/SiO_x substrates to check the DW chirality and the SHE-induced SOT (Extended Data Fig. 4):

• 6 Pt/2 Co/7 Ni/4 Co/30 Pt (sample ID MA5032): left-handed DW chirality and negative SHE-induced SOT and

• 6 Pt/4 Co/7 Ni/2 Co/30 Pt (sample ID MA5031): right-handed DW chirality and negative SHE-induced SOT.

Although the PMA is decent in these films, the anisotropy strength is smaller than for the 30 Pt/3 Co/7 Ni/3 Co films, thereby limiting the application of high current densities due to DW nucleation. The v–H_x curves are useful to determine the chirality of the interface DMI-induced chirality in Néel-type DWs and the sign of the SHE-induced SOT. The fields H_CR in the v–H_x curves, in which the velocity crosses through zero along the H_x axis are positive and negative for \(\odot \)⊗ and ⊗\(\odot \) DWs, respectively, the DW chirality is left-handed, and in which the velocity crosses through zero along the H_x axis are negative and positive for \(\odot \)⊗ and ⊗\(\odot \) DWs, respectively, the DW chirality is right-handed. By contrast, when the signs of the slope are negative and positive for \(\odot \)⊗ and ⊗\(\odot \) for positive currents J > 0, respectively, the sign of SHE-induced SOT is positive, and when the signs of the slope are positive and negative for \(\odot \)⊗ and ⊗\(\odot \) for positive currents J > 0, respectively, the sign of SHE-induced SOT is negative. For J < 0, the slope signs are reversed because of the reversed spin polarization in spin current, whereas H_CR does not change.

For 30 Pt/3 Co/7 Ni/3 or 1.5 Co that has been used for the twisting-dependent experiments in our paper, the DW is a left-handed Néel-DW and the SOT is positive, as shown in Extended Data Fig. 5a,b, thereby showing that the DW moves along the current flow direction in the absence of H_x (Extended Data Fig. 5a). Note that, for a given J, the DW velocities in the flat strips in Extended Data Fig. 5 are significantly larger than those from a ribbon having ζ = 0° shown in Fig. 3a. This shows that some imperfections and pinning sites in the ribbons significantly increase the threshold current density J_c, thereby reducing the DW velocity overall.

Right-handed Néel-type DWs (reversed DW chirality) are found in flat strips formed from the film stack 6 Pt/2 Co/7 Ni/4 Co/30 Pt on Si/SiO_x, as shown in Extended Data Fig. 5d (H_CR < 0 for \(\odot \)⊗ and H_CR > 0 for ⊗\(\odot \)). As the top Pt layer (30 Å) is thicker than the bottom Pt layer (6 Å), the sign of the SHE-induced SOT is reversed and negative, thereby leading to positive and negative slopes for for J > 0 and negative and positive slopes for DWs, respectively, for J < 0, as shown in Extended Data Fig. 5d. Consequently, the DW moves along the current flow direction in the absence of H_x (Extended Data Fig. 5c). Note that the DW velocities are low because of the competition between the interface-induced DMIs from the top and bottom interfaces, as compared with those with left-handed chirality and positive SHE-induced SOT from a single Pt layer.

To investigate how the SOT interacts with the geometrical twisting, we have additionally prepared twisted ribbons coated with the film stack 6 Pt/4 Co/7 Ni/2 Co/30 Pt that has a left-handed Néel-type DW and a negative SHE-induced SOT. As shown in Extended Data Fig. 5f, H_CR > 0 for \(\odot \)⊗ and H_CR < 0 for ⊗\(\odot \), whereas positive and negative slopes for \(\odot \)⊗ and, respectively, for J > 0, and negative and positive slopes for \(\odot \)⊗ and ⊗\(\odot \), respectively, for J < 0. Consequently, the DWs move along the electron flow direction in the absence of H_x as shown in Extended Data Fig. 5e. As for the right-handed Néel-type DWs and negative SHE-induced SOT, the overall DW velocities are significantly reduced.

First, a 6 Pt/2 Co/7 Ni/4 Co/30 Pt film that has a reversed DW chirality (right-handed) was grown on a left-handed twisted ribbon with ζ = −11° that corresponds to the left half of the twisted ribbon. As shown in Extended Data Fig. 6, the DW velocity for (2.49 ± 0.53 m s⁻¹) is larger than that for \(\odot \)⊗ (1.29 ± 0.20 m s⁻¹) at J = 6.4 × 10⁷ A cm⁻². This agrees with the prediction of our analytical model that the torsional torque is determined not only by the geometrical chiral twist but also by the DW chirality, as shown in Extended Data Table 2. Next, current-induced DW motions are measured from non-twisted and right-handed and left-handed twisted ribbons that were coated with 6 Pt/4 Co/7 Ni/2 Co/30 Pt films. Note that this film stack has a left-handed DW chirality and a negative SHE-induced SOT such that the DW moves along the electron flow direction (opposite to the current flow direction). Thus, J < 0 that is used during the measurements leads to v > 0. Note that DW velocities are measured only in the left-half region of the twisted ribbon. DW velocities for \(\odot \)⊗ are nearly identical to those for ⊗\(\odot \) for an untwisted ribbon as anticipated from our model (Extended Data Fig. 7). By contrast, a \(\odot \)⊗ DW moves faster than a ⊗\(\odot \) DW for the right-handed chiral twist (Extended Data Fig. 7b). This agrees with the model prediction (Extended Data Table 3). For a left-handed chiral twist, the DW velocity differences between the two DW configurations are not large (Extended Data Fig. 7c). This may be because DW velocities are overall very small (<5 m s⁻¹), thereby being more sensitive to pinning–depinning because of imperfections that can mask the torsional torque effect in the devices with reversed DW chiralities and SHE-induced SOT. Further improved fabrication processes that minimize such DW pinning–depinning will allow for clearer differences.