RNA neoantigen vaccines prime long-lived CD8+ T cells in pancreatic cancer

Trial design, patients and endpoints

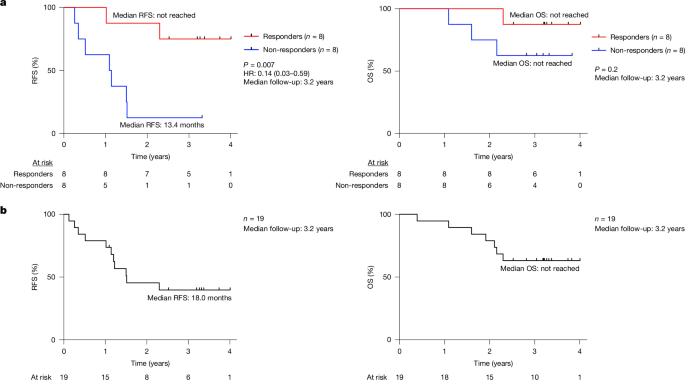
In our previously reported¹ single-centre, investigator-initiated, phase 1 clinical trial, patients with single, radiographically suspicious, surgically resectable PDAC, no distant metastases, and ≥5 neoantigens as predicted by our computational pipeline were treated with sequential surgery, adjuvant atezolizumab (anti-PD-L1), autogene cevumeran (an individualized vaccine based on uridine mRNA–lipoplex nanoparticles encoding up to 20 MHCI and MHCII restricted neoantigens) and mFOLFIRINOX. All patients had ECOG (Eastern Cooperative Oncology Group) performance status 0–1. We included patients with pathologically confirmed PDAC with surgical margin status R0/R1. We excluded patients with metastatic, borderline or locally unresectable PDAC and patients who received neoadjuvant therapy. The primary endpoint was safety. Secondary endpoints were 18-month RFS and 18-month OS. Additional eligibility criteria, procedures, treatments, and ethical study conduct have been described and are available in the protocol¹ (Supplementary File 1).

We treated 19 patients with atezolizumab (safety-evaluable cohort), of which 16 patients received subsequent autogene cevumeran (biomarker-evaluable cohort)¹. Fifteen of these 16 patients received subsequent mFOLFIRINOX. As described previously¹, vaccinated patients were classified as autogene cevumeran (vaccine) responders if they generated high-magnitude T cell responses to vaccine neoantigens assessed by a previously described ex vivo IFNγ ELISpot assay²⁹ that detects vaccine-induced T cell responses and does not distinguish CD8⁺ from CD4⁺ T cell responses.

We defined recurrence as new lesions by response evaluation criteria in solid tumours (RECIST, version 1.1). We defined RFS from either the date of surgery (RFS) or from the date of the last autogene cevumeran priming dose (landmark RFS) to the date of recurrence or death, whichever occurred first. We defined OS from the date of surgery to the date of death. We censored patients without events at the last known date they were recurrence-free. We defined the recurrence window as the time frame from surgery when ~80% of patients recur^2,3,4. Data cut-off was 1 December 2023, extending the median follow-up to 38 months.

We conducted the study in accordance with the Declaration of Helsinki and good clinical practice guidelines. The study was approved by the institutional review board (IRB) at Memorial Sloan Kettering Cancer Center (MSK), the United States Federal Drug Administration (FDA), and was registered on clinicaltrials.gov (NCT04161755). All participants provided written informed consent.

Mutation identification and neoantigen selection for personalized vaccines

We previously reported detailed characteristics of vaccine neoantigen selection¹. In brief, we identified expressed non-synonymous mutations and HLA type by whole-exome sequencing of patient-specific tumour–normal pairs and tumour RNA sequencing. We then bioinformatically estimated neoantigens and ranked neoantigens by immunogenicity as previously described³⁰.

Autogene cevumeran manufacture

As reported¹, for every patient, we manufactured individualized mRNA neoantigen vaccines under good manufacturing practice conditions as two uridine-based mRNA strands with noncoding sequences optimized for superior translational performance^31,32. We designed each strand to encode up to 10 MHCI and MHCII neoantigens formulated in approximately 400-nm diameter lipoplex nanoparticles²⁶ that comprised the synthetic cationic lipid (R)-N,N,N-trimethyl-2,3-dioleyloxy-1-propanaminiumchloride (DOTMA) and the phospholipid 1,2-dioleoyl-sn-glycero-3-phosphatidylethanolamine (DOPE) to enable intravenous delivery.

Patient samples, cell lines and cell culture

We purified patient PBMCs by density centrifugation over Ficoll-Paque Plus (GE Healthcare) and cultured purified cells in RPMI medium supplemented with 10% fetal bovine serum (FBS, Nucleus Biologics), 1 mM sodium pyruvate, 2 mM l-glutamine, non-essential amino acids and 2-mercaptoethanol, 100 U ml⁻¹ penicillin-streptomycin (MSK medium preparation core facility), with 100 U ml⁻¹ IL−2 (Peprotech) and 100 U ml⁻¹ IL-15 (Peprotech) added every other day. To map single clone reactivity, we purchased pan negative selection purified human T cells (Precision for Medicine) and cultured purified T cells in RPMI medium (Gibco, Thermo Fischer Scientific) supplemented with 10% FBS (Sigma-Aldrich), 100 U ml⁻¹ penicillin-streptomycin (Gibco, Thermo Fischer Scientific), 1,000 U ml⁻¹ IL-7 (Peprotech, Thermo Fischer Scientific), 100 U ml⁻¹ IL-15 (Peprotech, Thermo Fischer Scientific) and 4 mM l-glutamine (Gibco, Thermo Fischer Scientific). We cultured T2 and K562 cells with RPMI medium (Gibco, Thermo Fischer Scientific) supplemented with 10% FBS (Sigma-Aldrich) and 100 U ml⁻¹ penicillin-streptomycin (Gibco, Thermo Fischer Scientific). We cultured Phoenix-AMPHO and RD114-envelope producer cells with DMEM medium (Gibco, Thermo Fischer Scientific) supplemented with 10% FBS (Sigma-Aldrich) and 100 U ml⁻¹ penicillin-streptomycin (Gibco, Thermo Fischer Scientific). We froze tumour, adjacent tissue and draining lymphatic tissue samples from resected tumour specimens for subsequent analysis.

HLA cloning and transduction

We cloned patient-matched HLA alleles and transduced T2 and K562 cells as previously described¹. In brief, we cloned HLA alleles followed by an IRES GFP reporter into a SFG γ-retroviral vector and transfected Phoenix-AMPHO cells using Lipofectamine 3000 (Thermo Fisher Scientific). We collected vector-containing supernatants and used them to transduce T2 and K562 cells by spinoculation in the presence of Polybrene (EMD Millipore). We sorted HLA⁺ K562 cells and GFP⁺ T2 cells using an Aria Cell sorter (BD Biosciences).

TCR reconstruction, cloning, transduction and peptide stimulation

We reconstructed and cloned TCRs as previously described¹. In brief, we identified T receptor beta (TRB) V-D-J and T receptor alpha (TRA) V-J sequences from purified, sequenced single T cells and fused them to modified mouse constant TRB and TRA chain sequences, respectively. Then, we joined TRB and TRA chains with a furin SGSG P2A linker and cloned them into a SFG γ-retroviral vector. We transduced human pan T cells as previously described¹ with minor modifications. In brief, we transfected Phoenix-AMPHO cells with SFG γ-retroviral vectors using Lipofectamine 3000 (Thermo Fisher Scientific). Then, we used vector-containing supernatants to transduce RD114-envelope producer cells. We sorted transduced cells to generate stable cell lines and concentrated vector-containing supernatants using Retro-X Concentrator (Takara). We activated human pan T cells with CD3/CD28 beads (Thermo Fisher) and transduced them at day 3 post-activation in a Retronectin (Takara) coated plate using concentrated vector-containing supernatants. Transduction efficiency was confirmed by flow cytometry gating on live CD8⁺ mTCR⁺ cells.

To select possible neoantigen epitopes to test TCR specificity and binding, we generated all possible unique 8–14mers out of all full-length (18–27mer) immunogenic (ELISpot-positive) vaccine neoantigens. We predicted binding of each of these 8 to 14mers to the patient’s HLA-I by NetMHCPan4.1. We further selected peptides with binding affinities <1000 nM or predicted strong binders (as per NetMHCPan4.1) for further testing and peptide stimulation.

We stimulated TCR-transduced T cells with peptides as follows: we pulsed 2.5 × 10⁵ HLA-transduced T2 or K562 cells in a 96-well U-bottom plate at 37 °C with the indicated peptides at the indicated concentrations for 1 h. Then, we centrifuged and washed the peptide, added 5 × 10⁴ TCR (effector:target ratio of 1:5) or mock (control) transduced T cells per well, and measured CD137 (4-1BB) expression on CD8⁺ mouse TCR⁺ T cells after 24 h in coculture. To calculate the avidity of a TCR for its cognate epitope and the corresponding wild-type peptide, we stimulated TCR-transduced T cells with antigen-presenting cells pulsed with different concentrations of mutant or wild-type peptide (range from 100 μM to 10⁻⁵ μM), performed a nonlinear regression to fit the data to a sigmoidal curve, and calculated the EC₅₀ as the peptide concentration that activates 50% of the TCR-transduced T cells. When a TCR did not show reactivity with an EC₅₀ value tending towards infinite, we assigned the EC₅₀ to be 1,000 μM.

Immune response

TCR Vβ sequencing

We extracted gDNA from bulk PBMCs, purified T cells and patient tissue samples using a DNA extraction kit (Qiagen). We used Dropsense 96 to quantify samples, dilute standard concentrations, and prepare libraries. We then generated sample data using an immunoSEQ Assay (Adaptive Biotechnologies), as previously described¹. In brief, we amplified the somatically rearranged TCRB CDR3 using a two-step, amplification bias-controlled multiplex PCR reaction, that contains forward and reverse amplification primers specific to every known V and J gene segment and amplifies the CDR3 receptor hypervariable locus, followed by a second PCR to add barcode and Illumina adapter sequences³³. Reference gene primers in the PCR further quantify total nucleated cells available for sequencing, and thus measure the fraction of T cells in each sequenced sample. The CDR3 and reference gene libraries were then sequenced, raw sequence reads demultiplexed per Adaptive’s barcode sequences, and demultiplexed reads processed to remove adapter and primer sequences and identify and remove primer dimer, germline and contaminant sequences. Relative frequency ratios between similar clones and a modified nearest-neighbour algorithm were used to cluster the filtered results, and merge closely related sequences to correct for sequencing induced technical errors. The output sequences were then annotated to the V, D, and J genes and N1 and N2 regions that constitute each unique CDR3, and the corresponding encoded CDR3 amino acid sequence. We defined annotated genes per the IMGT database (https://www.imgt.org). The output TCR V CDR3 sequences were then normalized and corrected for residual multiplex PCR amplification bias and quantified versus synthetic TCRB CDR3 sequence analogues³⁴.

Single-cell RNA and TCR sequencing

As reported¹, we prepared libraries for single-cell immune profiling, sequenced and post-processed raw data at the Epigenomics Core at Weill Cornell Medicine.

Sample preparation

To analyse the gene expression of vaccine-induced clones, bulk T cells from patient-derived PBMCs were purified by fluorescence-activated cell sorting and sequenced as previously reported¹. In brief, we purified single T cells and prepared scRNA-seq libraries as per company specifications prior to performing single-cell immune profiling (10x Genomics, guide CG000330). Each cellular suspension at 97% viability and at 950 cells per μl was loaded onto to a Chromium X to generate Gel Beads-in-Emulsion (GEM) targeting 10,000 single cells per sample.

Sequencing and data processing

To generate 5 P expression libraries, we enzymatically fragmented an aliquot of the cDNA (~50 ng), and end-repaired, A-tailed, subjected to a double-sided size selection with SPRI select beads (Beckman Coulter), and ligated to adaptors. We then introduced a unique sample index for each library through 14 cycles of PCR amplification using the indexes (98 °C for 45 s; 98 °C for 20 s, 54 °C for 30 s and 72 °C for 20 s × 14 cycles; 72 °C for 1 min; held at 4 °C), subjected indexes to a second double-sided size selection, and quantified libraries using Qubit fluorometric quantification (Thermo Fisher Scientific). We assessed quality on an Agilent Bioanalyzer 2100, obtaining an average library size of 460 bp. To generate full-length TCR VDJ regions, we subjected cDNA aliquots (5 ng) to nested PCR amplification with specific VDJ outer and inner primer pairs (98 °C for 45 s; 98 °C for 20 s, 67 °C for 30 s and 72 °C for 20 s × 8 cycles; 72 °C for 1 min; held at 4 °C), 1-sided size selection using SPRI select beads, and assessed quality and quantity of the VDJ region using an Agilent Bioanalyzer 2100. The average library size was 620 bp.

We then clustered gene expression and TCR libraries on an Illumina Novaseq pair end flow cell sequenced for 28-10-10-91, to obtain about 350 million clusters per sample. We processed sequencing images using Illumina’s Real Time Analysis software (RTA). We used 10x Genomics Cell Ranger Single Cell Software suite v6.0.0 (https://support.10xgenomics.com/single-cell-gene-expression/software/pipelines/latest/what-is-cell-ranger) to demultiplex, align (hg19), filter, UMI count, and single-cell 5′ end gene count samples, assemble TCRs, annotate paired VDJ, and perform quality control per manufacturer’s parameters.

CloneTrack

Clone definition

We defined a T cell clone by the nucleotide CDR3 sequence of the β chain and its V and J genes (TRB). For T cells identified by single-cell sequencing, we defined clones by the CDR3B nucleotide sequence, and mapped clones to paired TCR Vβ sequencing. The V/J genes were disregarded to remove cross-platform biases in V/J gene calling.

We defined the frequency of a clone x as \(f_x\,=\fracn_xN\), where n_x is the number of reads corresponding to the clone x as defined above, and N is the summation of all productive (in-frame, no stop codons) reads, as done previously¹.

We computed the aggregate frequency of several clones \(x\in X\) using an aggregate count \(n_X=\sum _x\in Xn_x\) and used a pseudo-frequency as previously described¹ if \(n_X=0\).

We defined vaccine-induced and atezolizumab (anti-PD-L1)-induced clones as previously described¹. In brief, in CloneTrack, we select a baseline timepoint, and a time period of interest, and compute P values for each clone to determine if it expands twofold or greater within the determined time period, using a modified Fisher exact test as previously described¹, with Bonferroni multiple hypothesis testing adjustment for both the clones and the number of timepoints examined. We select the most significant timepoint for each clone with an adjusted P < 0.001. For vaccine-induced CloneTrack clones, we use the timepoint immediately preceding the vaccine priming dose as the baseline and define the expansion time period to extend until the first dose of chemotherapy (after completing all priming doses). We impose a de novo constraint on prime clones, such that the clones must not be detected in blood before the start of the priming doses. For anti-PD-L1-expanded clones, we use the timepoint immediately preceding the anti-PD-L1 dose as the baseline and define the expansion time period to extend until period immediately after anti-PD-L1. Our updated analyses yield identical clones as detected previously¹.

We defined a clone induced by a vaccine boost by modifying the above described modified Fisher exact test¹ with a twofold expansion factor between the timepoints immediately pre- and post-boost, together with a de novo constraint and a significance threshold of adjusted P < 0.001 after accounting for the Bonferroni multiple hypothesis correction. No induced vaccine boost clones were found.

Half-life and lifespan

As we have sufficient timepoints in our CloneTrack time series, we can utilize a standard mathematical method to estimate half-life and lifespan in biological and physical systems—fitting an exponential function to experimentally observed decay rates of individual T cell clones. For each clone, we plot the experimentally measured trajectory (Extended Data Fig. 4e, top), and then derive the half-life and lifespan for the clone after priming doses alone and after priming + boost doses as described below.

1. (1)

   To estimate the clone half-life and lifespan post-priming, we identify the peak priming time (time when the clone’s frequency peaks before boost), and select all times from peak priming to boost (Extended Data Fig. 4e, top, orange circles).

2. (2)

   To estimate the clone half-life and lifespan post-prime/boost, we identify the peak boost time (time of the clone’s first measured frequency post-boost), and select all times post peak boost.

When a clone is not detected (frequency = 0), we impute its frequency \(f_\rmimputed=0.5/\max \_\rmsample\_\rmnorm\) where \(\max \_\rmsample\_\rmnorm\) is the total sequence count in the largest sequencing sample in the time series.

We then hypothesize that the frequency of a clone exponentially decays as a function of time:

where f(t) = clone frequency at time t; f₀ = peak clone frequency; τ = mean lifetime. There are two free parameters, \(f(t)\) and \(t_1/2\), which must be inferred. To infer the free parameters for each of these curves, we performed a linear fit on the log of the clone frequencies using a least-square regression (implemented using stats.linregress).

We take \(t_=0\) by subtracting peak time from all subsequent times, and linearize the exponential equation:

We can now fit a linear regression to the above equation to derive the decay constant, \(\tau \). The fitted slope is \(m=-\,\frac1\tau \). Therefore:

As the half-life of a clone is the time for a clone to reduce from its peak frequency by 50%,

Where m is the fitted slope from the observed trajectory.

We define lifespan as time for a clone’s frequency to fall below the detection threshold (10⁻⁶). We derive the lifespan (t_{disappearance}) as:

The two quantities we report from these fits are the half-life (\(t_1/2\)), and the lifespan (t_{disappearance}). These estimated values were then clipped at maximum values of 5 years for the half-life \(t_1/2\), and 100 years for the disappearance time \(\Delta t_d\), including for any clones which were growing instead of shrinking, which would infer negative half-lives and lifespan.

To estimate goodness of fit, we calculate the root mean square error (RMSE) that measures for each clone, how far each estimated point is from the observed frequency at that timepoint, averaged across the time series.

Specifically, the RMSE is calculated as

Where N is the number of points being fitted, \(y_i^\prime \) is the estimated frequency at timepoint i and y_i is the observed frequency at timepoint i.

We calculate the RMSE in the natural log space in which the equation is fitted and visualize the RMSE (Extended Data Fig. 4e, bottom) on a log₁₀ scale, equivalent to the scale we plot the clone trajectories (Fig. 2b and Extended Data Fig. 2a). All estimated frequencies are within a factor of 10 of the observed frequencies, and 98 of 144 (68%) of estimated frequencies fits lie within a factor of 2 of the observed values.

CloneTrack survival curves

The survival curves of CloneTrack clones were determined based on time from first observation of the clone. As all of these clones were unobserved in the blood pre-vaccination, this appearance time (t_a) can be determined precisely. For the observed survival time (\(t_s\)), we took the difference from the last timepoint a clone is observed to the appearance time. For the estimated survival curves we determined the survival time using the disappearance time \(\Delta t_d\) and the start time \(t_\) (either peak prime frequency or post-boost follow-up time) for that fit:

Note, patient 5 did not receive a boost, so their two CloneTrack clones are included in both the prime and total estimated survival curves.

Time integrated cumulative vaccine frequency

To measure the cumulative frequency of the CloneTrack clones up to a set point in time we computed an integrated average of the aggregate CloneTrack frequency time series. As T cell clone frequencies change on a logarithmic scale, we integrated and averaged the log of the frequency trajectory and then exponentiated at the end (a weighted geometric mean);

Where \(p_c(t)\) is the frequency trajectory of CloneTrack clone c. To avoid taking logs of zeros we used a minimum frequency of 2 × 10⁻⁶ if no CloneTrack clones were measured at a timepoint. We used a time t = 644 days for analysis, corresponding to the latest follow-up timepoint at which complete clonal analysis is available for all patients. The numerical integration was done using scipy.integrate.cumtrapz.

Metaclones

To find additional T cell clones that may be responding to the vaccine, we looked for clonotypes with TCR sequences similar to the vaccine-reactive clones (that is, CloneTrack clones). We used GLIPH2.0³⁵ with default parameters to cluster all beta chain TCRs (including CDR3 amino acid sequence, V and J gene) of each patient using most available TCR sequencing samples for that patient (restricting samples to early follow-ups). Among the GLIPH groups that were labelled as significant (Fisher score <0.05) compared with the background CD4/CD8 reference TCRs provided by GLIPH2, we identified those containing CloneTrack clones (vaccine-responding metaclones). For each patient, TCR clones (defined by their nucleotide sequence and V/J genes) with CDR3 amino acid sequences belonging to each vaccine-responding metaclone were identified at each timepoint and the sum of the frequencies of these clones (excluding the original CloneTrack clones) was plotted for all available timepoints.

Single-cell analysis

Quality control

Filtered count matrices generated by Cellranger (v6) were integrated into a single matrix using Scanpy³⁶. Cells were filtered by having a sequenced high confidence TRB CDR3 region called from Cellranger VDJ (v6). Genes were further filtered based on whether the distribution of the gene expression over the set of cells that express the gene (non-zero expression) has at least 1 nat of entropy and the gene was found in at least 1% of total cells. Both mitochondrial and ribosomal genes were removed.

Phenotyping

Phenotyping was done using the GeneVector pipeline³⁷. Cells and genes that pass quality control are embedded according to the GeneVector methodology using mutual information signed by the correlation coefficient into a 20-dimensional latent space³⁸. Phenotyping was then done on cells belonging to CloneTrack clones (as identified by their TRB sequences) by fitting a gaussian mixture model with three components to the cosine similarity of each cell embedding vector onto five genes embedding six vectors (MKI67, GZMB, ZNF683 and KLF2) as implemented in Scikit-Learn³⁹.

PhenoTrack

We generated PhenoTrack plots using the phenotyping method described above. Each PhenoTrack plot is defined by examining a set, C, of T cell clones for a particular individual, and tracks the relative frequency, and flow of phenotypes of each clone. As clones can expand or disappear in the repertoire, these plots differ from standard Sankey and alluvial plots in that there is no balanced flow in and out of nodes. To define these plots, we first calculated the frequency of each phenotype f_i for each clone c at each timepoint T, \(p_c,T(\,f_i\,))\). This can be represented as a sum over all cells x that have clonotype c (indicated as \(x \sim c\)):

Where X_T is the set of sequenced clones at timepoint T, N_T is the total number of cells in X_T, and \(p(\,f_i\,|x)\) is the probability cell x has phenotype f_i (if using deterministic assignments this is either 0 or 1). The static phenotype breakdown of each sequenced timepoint can be easily determined by summing over all clones in C:

This is represented by the solid bars at the sequenced points. We can never determine phenotype swapping of individual cells, as any cell that was sequenced is necessarily not present at the next timepoint, so to determine phenotype flow from one point to the next we examined the phenotype probabilities of clones. It is also important to note that as a clone c may not have the same frequency at timepoint T as at timepoint T + t, the total flow out from a timepoint may not equal the flow into the next timepoint. This necessitated us to define both outflow and inflow between adjacent timepoints. The phenotype flow out from a phenotype f_i to f_j for an individual clone c between timepoints T and T + t can be defined according to an independent approximation:

The inflow for this same transition only differs in the clone frequency normalization:

To get the total flows over our clone set C we need only sum over the clones \(c\in C\):

and

These outflows and inflows, along with a simple Hill function interpolation between the two, determine the width of the bands showing the transitions between phenotypes. Each band is coloured based on the phenotype it flows out of. Also note, that because a clone may not be present at both timepoints the total flow in/out of a timepoint may not equal the static probabilities, that is:

and

indicating clones either leaving or entering the repertoire at those respective timepoints. For PhenoTrack plots that aggregate over individuals, all of these equations were averaged over the individuals.

We define pre/post-vaccination phases as follows:

• Expansion: all time periods during priming doses of autogene cevumeran

• Contraction: all time periods after priming doses of autogene cevumeran and before mFOLFIRINOX

• Early memory: 0.8–1.8 years post-vaccination

• Mid memory phase: 1.9–2.3 years post-vaccination

• Late memory phase: all time periods from 2.4 years onwards

Ternary plots

The ternary plots were generated by reducing the phenotype space to three phenotypes and determining the phenotype breakdown of each clone of interest only with respect to these phenotypes:

These 3D probability vectors can then be plotted on the 2D simplex. Single timepoints can be represented as a scatter plot and transitions between timepoints can be represented by arrows. The width or size of a marker represents the frequency of the clone at the initial timepoint. Clones can also be aggregated together by summing and renormalizing.

P
_gen

The probability of each amino acid CDR3 TRB to be generated through VDJ recombination, also known as P_gen, was computed using the OLGA software⁴⁰. P_gen was computed for each TRB in all baseline samples for responding patients using the default human TRB IGoR model⁴¹ shipped with OLGA. Each P_gen was computed for the amino acid CDR3 TRB excluding V and J gene restrictions.

Gene-expression analysis

For the differential gene analysis, we specifically examined only cells belonging to CloneTrack clones in patients 1, 6, 10, 11, 14 and 29 (n = 9,110 cells). We normalized the gene expression by the total number of counts in each cell (implemented by scanpy.normalize_total) and computed log gene expression on the normalized genes expression (implemented by scanpy.logp1):

where GE(c,g) is the read count of gene g in cell c.

We computed the differential gene heatmap between phases phase-by-phase. Only genes that were not ribosomal or mitochondrial were considered (n = 24,800). For each phase, we identified genes that were the most significantly upregulated in cells from that phase relative to all other (CloneTrack) cells using Mann–Whitney U with Bonferroni multiple hypothesis correction with an adjusted P value threshold of 0.001. Genes that passed significance were then ordered by their mean differential log₂ gene expression:

where Ph indicates the cells from a particular phase. We depict the top 25 upregulated genes from the phases: expansion, contraction, memory as a heatmap composed of the differential expression for each of these genes at each of the above phases (Fig. 3d).

We generated the gene expression violin plot for a gene g by using the LGE(c,g) of that gene for cells of the labelled phases.

We perform gene set enrichment analysis to confirm genes expressed by vaccine-induced T cells in the expansion phase are modulated by proliferating T cells⁴² (gene set: Travaglini_Lung_Proliferating_NK_T_Cell, P value = 2.3 × 10⁻²², false discovery rate q value = 3.7 × 10⁻¹⁹), and in the contraction phase modulated by CD8⁺ T cells post-antigen exposure (gene set: Kaech_Day8_Eff_VS_Memory_CD8_TCell_DN, P value = 7.8 × 10⁻¹⁸, false discovery rate q value = 5.4 × 10⁻¹⁵).

Whole-exome sequencing, mutation identification and phylogeny

We applied the same bioinformatic pipeline as previously described²⁸. In brief, we aligned reads to the reference human genome (hg19) using BWA (v0.7.17)⁴³, and marked duplicates by picard-2.11.0 MarkDuplicates (https://broadinstitute.github.io/picard/). Then, we performed indel realignment by the Genome Analysis toolkit (GenomeAnalysisTK-3.8-1)⁴⁴ using RealignerTargetCreator and IndelRealigner. We used the 1000 genome phase1 indel (1000G_phase1.indels.b37.vcf) and Mills indel calls (Mills_and_1000G_gold_standard.indels.b37.vcf) as references. We then calibrated base quality by the GATK’s BaseRecalibrator using dbSNP version 138 as reference source. After a pre-processing step, we employed MuTect 1.1.7⁴⁵ and Strelka 1.0.15⁴⁶ to identify SNVs and indels in tumour samples compared to normal tissue. Using bam-readcounts (v0.8) (https://github.com/genome/bam-readcount), we counted the number of reference and alternative alleles at each mutation position. We then filtered mutations by coverage and variant allele frequency (VAF) by the following criteria: (1) total coverage for tumour ≥10; (2) VAF for tumour ≥4%; (3) number of reads with alternative allele ≥9 for tumour; (4) total coverage for normal ≥7; and (5) VAF for normal ≤1%. After filtering, we took union of filtered mutations within each individual, leveraging primary and recurrent samples. This allowed us to capture coverage and VAF changes from primary to recurrent tumours, even for undetected mutations. We repeated the bam-readcount step for this union set of mutations. Since VAF is not a normalized measure to represent cancer cell fraction (CCF), we used phyloWGS (v1.0-rc2)⁴⁷ to reconstruct the phylogeny tree and also to infer CCF on the merged set of mutations. Primary and recurrent tumours share the same topology, but the CCF can differ between primary and recurrent samples. We chose the tree for each sample that has the largest likelihood value. We visualized trees with R package data.tree (v1.1.0) (https://cran.r-project.org/web/packages/data.tree/index.html). The colour represents CCF changes from primary to recurrent tumours in log scale (log CCF_rec/CCF_prim).

In vitro peptide stimulation

For each neoantigen, we designed 2–4 overlapping 15mer peptides (OLPs, Genscript) covering the mutated neoantigen sequence encoded by the RNA vaccine (Genscript). We resuspended all peptides in DMSO at 10 mg ml⁻¹. Then, we cultured 1 × 10⁶ PBMCs in a 48-well plate with peptide pools (total peptide concentration of 20 μg ml⁻¹) added on day 1, and IL-2 (100 U ml⁻¹) and IL-15 (10 ng ml⁻¹) added on day 2 and every subsequent 2–3 days. Then, on day 7 we restimulated PBMCs with peptide pools, and analysed T cell degranulation by incubating stimulated cells for 1 h with an anti-CD107a antibody, and T cell TNFα and IFNγ production by incubating stimulated cells for 4 h at 37 °C with a protein transport inhibitor (BD Biosciences) and measuring intracellular cytokine production by flow cytometry.

Epitope spreading

To detect epitope spreading in responders, we stimulated PBMCs in vitro with neoantigens not encoded in vaccines. First, we used WES to identify somatic mutations as described above. Then, we filtered out mutations either included in the vaccine, called with low confidence, or whose transcript encoded an amino acid sequence present in the patient reference proteome (that is, we excluded synonymous, stop gain, and start loss mutations). From this set, we computationally created 27mers with the mutated residue at position 14 (where fewer than 13 amino acids were available before or after the mutated residue, all available residues were included), tested binding of 27mer derived 8 to 14mer neoepitopes (excluding all k-mers that did not span the mutation site) to the patient’s HLA-I by NetMHCPan4.1, and selected 27mers containing at least one neoepitope predicted to be a strong binder (as per NetMHCPan4.1) or with a binding affinity²⁷ <150 nM. We then designed 2–4 OLPs (Genscript) covering the mutated 27mer and performed in vitro peptide stimulations of bulk PBMCs as described above.

Flow cytometry and cell sorting

We analysed PBMCs and transduced T cells on a FACS LSR Fortessa (BD Biosciences) using FACSDiva software (version 8.0.1, BD Bioscience). We stained cells for cell surface and intracellular markers using antibody cocktails per manufacturer’s recommendations, in a final staining volume of 100 µl, with appropriate controls as indicated. We used the following antibodies and reagents: from BioLegend, CD137 (clone 4B4-1, PE; 3 µl per sample), CD3 (clone SK7, PE-Cy7; 4 µl per sample), CD4 (clone OKT4, Brilliant Violet 650; 2 µl per sample), CD45 (clone 2D1, Alexa Fluor 700; 5 µl per sample), CD56 (clone HCD56, BV605; 2 µl per sample), CD8 (clone SK1, AF700 and APC-Cy7; both 2 µl per sample), HLA_ABC (clone W6/32, APC; 3 µl per sample), IFNγ (clone 4S.B3, BV421; 5 µl per sample), and mTCR (clone H57-597, PE-Cy5; 0.5 µl per sample); from BD Biosciences, CD107a (clone H4A3, PE; 20 µl per sample), CD56 (clone NCAM16.2, BV786; 5 µl per sample), TNFα (clone Mab11, APC; 2.5 µl per sample), and DAPI (564907; 0.2 µl per sample); and from Invitrogen, fixable viability Dye eFluor 520 (65-0867-14; 1.0 µl per sample). We used the following definitions: human T cells as live, CD45⁺CD56⁻CD3⁺ cells; degranulating CD8⁺ T cells as live, CD56⁻CD3⁺CD8⁺CD107a⁺; neopeptide-stimulated CD8⁺ T cells as live, CD56⁻CD3⁺CD8⁺TNFα⁺IFNγ⁺; and activated transduced T cells as live, CD3⁺CD8⁺mTCR⁺4-1BB⁺. We sorted T cells using an Aria Cell sorter (BD Biosciences). We analysed the data using FlowJo (version 10).

Identification of T cell clones through in vitro neoantigen rechallenge

In vitro neoantigen-specific T cell clones were identified as previously described¹ with minor modifications. In brief, to determine if a T cell clone was specifically stimulated by a neopeptide pool, we sort-purified T cell clones into activated and inactivated fractions (CD107a⁺ and CD107a⁻) after peptide stimulation for either TCR Vβ or single-cell VDJ sequencing.

To identify antigen-specific T cell clones, we determined a peptide-specificity stimulation P value for each T cell clone using a one-tailed binomial test (implementing the scipy.stats.binom_test) with a threshold S, to indicate significance with respect to at least S fraction of a clone being antigen-activated. We set the threshold such that no expanded T cell clones were detected in the control (DMSO) PBMCs for the experiment, by sweeping all thresholds from 0 to 1 with steps of 0.1. The minimum threshold which gave no expansion in each DMSO control was selected and an extra step of 0.1 was then added to enforce higher specificity of the expanded clones identified in the experiment. We defined clones based on the nucleotide sequence of the TRB junction. We adjusted P values using Bonferroni correction and determined significance at an adjusted P value threshold of <0.001.

Statistical analyses

Sample sizes (n) represent the number of patients, samples, clones or cells. We analysed survival curves by log-rank (Mantel–Cox) test, compared two groups using unpaired two-tailed Mann–Whitney test, paired groups with two-tailed paired t-test or two-tailed Wilcoxon matched-pairs signed rank test, multiple groups with Kruskal–Wallis test, categorical variables by chi-squared test, and correlated parameters with Spearman correlation. We compared longitudinal clonal expansion by two-tailed Fisher’s exact test, and in vitro clonal activation by binomial test with Bonferroni correction. For differential gene-expression analysis, we used Wilcoxon rank sum without any multiple hypothesis correction. P < 0.05 was considered statistically significant. All analyses were performed using GraphPad Prism (version 10.1.1) or Python (version 3.11.6).

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.