Community estimate of global glacier mass changes from 2000 to 2023

GlaMBIE (https://glambie.org) is a community effort to compile, homogenize, combine and analyse regional estimates of glacier mass changes from four distinct observation methods, or hybrids of observation methods: glaciological observations, DEM differencing, altimetry and gravimetry (Extended Data Fig. 1). In total, we analysed 233 regional estimates of glacier mass changes from about 450 data contributors organized in 35 research teams (Supplementary Tables 1 and 2). Data contributions were compiled through an open call for data submission and selected based on expert evaluation of their confidence levels. Within each observation method, the selected input data were homogenized for time, space and unit domains using common corrections. They were then combined first within and second among methods for each of the 19 regions and finally aggregated to global estimates. Below, we briefly summarize the input data (Extended Data Fig. 1) and the general workflow (Extended Data Fig. 2) of our intercomparison exercise, including key equations. The full methodological details are available in our code (‘Code availability’). For more information on the different observation methods, we refer to a recent review on measuring glacier mass changes from space²⁶ and the methods references of our input data as listed in Supplementary Table 1. As an output, GlaMBIE provides the native input data in a standardized format, combined estimates per observation method and combined estimates among observation methods (‘Data availability’). Given the available data, we consider our combined estimate (among methods) to best reflect the expert evaluation of the GlaMBIE community.

Glacier regions

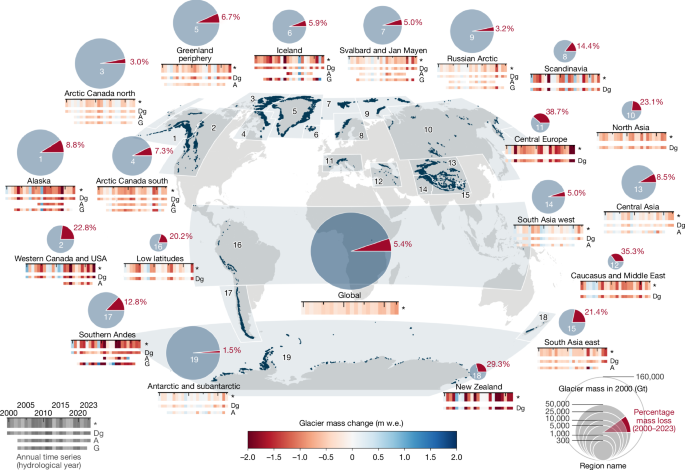
We used the 19 first-order glacier regions defined by the Global Terrestrial Network for Glaciers⁵¹. These regions appear suitable for glacier studies owing to their manageable number and geographical extent, which in most cases is close to the spatial correlation distance of the variability of glacier mass change, which is several hundred kilometres^25,52. In our analysis, we differentiate between regions with a large glacier area (>15,000 km²) and regions with a small glacier area (<15,000 km²).

Glacier area, volume and mass in 2000

We aggregated the regional glacier area from the Randolph Glacier Inventory (RGI 6.0)^19,53. This snapshot inventory provides one digital outline and a corresponding area for each glacier in the world. Although RGI aims for a reference year in 2000, the regional (area-weighted average) reference years deviate by up to 22 years (Extended Data Table 4). To account for glacier shrinkage, we used regional glacier area-change rates (percent per year) compiled from IPCC AR5⁴⁷ (Ch. 4, Fig. 4.10 and Table 4.SM1), extended with additional literature from Zemp et al.²⁵. With these annual area-change rates, we corrected glacier area from RGI 6.0 to the year 2000 (Table 1) and computed yearly time series (t_y) of regional glacier area (S in km²):

where \(S_t_\) is the regional glacier area in the (area-weighted average) reference year t₀ and δS/δt is the annual area-change rate (in percentage). It is noted that the latest version of RGI (7.0)^54,55 was not used as it only became available after the launch of the GlaMBIE, and its full implementation in glacier mass-change assessments will take a few years. Regional glacier volume and mass are from a multi-model consensus ice-thickness estimate²⁰, which was based on glacier outlines from RGI 6.0. We used their estimates relevant to sea-level rise, that is, subtracting the ice fraction below present-day sea level. In addition, we corrected their values to the year 2000 (Table 1) by using annual mass changes after 2000 from our combined estimate (see below) and before 2000 from the input dataset of Dussaillant et al.⁵⁶, which provides mass-change estimates from 1976, combining glaciological observations with DEM differencing. For regional glacier area and related changes over time, we assume a general uncertainty of ±5% based on a glacier mapping intercomparison study⁵⁷. Uncertainties for glacier volume and mass are from the multi-model consensus ice-thickness estimate²⁰.

Glaciological observations

This approach determines glacier mass changes traditionally in the unit metre water equivalent (1 m w.e. = 1,000 kg m⁻²) from in situ observations of accumulation and ablation, generally based on measurements at stakes and in snow pits⁵⁸. The method provides surface mass changes from a few hundred glaciers distributed in almost all glacier regions over seasonal-to-annual timescales with some records beginning in the late-nineteenth century^21,24. We analysed glaciological observations from the World Glacier Monitoring Service^24,59. The data cover the period from 2000 to 2023 and are available for all but two glacier regions (Extended Data Fig. 1 and Supplementary Table 1). We replaced the data gaps in Arctic Canada south with observations from Arctic Canada north and the gaps in the Russian Arctic with observations from Svalbard. We only used the interannual variability from glaciological observations, which is considered high confidence^25,52 owing to its spatial correlation over several hundred kilometres^60,61. The long-term trend, however, was not used owing to the sparse spatial coverage (typically well below 10%) and limited representativeness of the glaciological samples concerning total mass changes^44,62,63,64. Also, the glaciological method does not account for ice discharge of marine-terminating glaciers, which is a relevant mass-loss component in some regions³⁴ and implicitly accounted for in DEM differencing, altimetry and gravimetry. Consequently, we combined the temporal variability from the glaciological observations with long-term trends from DEM differencing (Extended Data Fig. 2).

DEM differencing

This approach determines glacier elevation change (traditionally in the unit of metres) by repeated mapping of glacier surface elevations, such as from optical stereo photogrammetry or synthetic aperture radar interferometry^26,46. The method provides multi-annual elevation differences, ideally corrected for vertical land motion⁶⁵, and requires density assumptions for converting to geodetic mass changes²⁹. DEM differencing represents glacier mass changes above sea level as it implicitly accounts for calving owing to ice discharge (contributing to sea-level rise), but it does not include any mass changes below water level (not contributing to sea-level rise) owing to the retreat or advance of lake- and ocean-terminating glaciers³⁴. We used 42 geodetic estimates from DEM differencing from 12 research teams covering all glacier regions and the entire period since 2000 using various methods^{27,46,66,67,68,69,70,71,72,73,74,75,76,77,78} (Extended Data Fig. 1 and Supplementary Table 1). The regional assessments used various optical (for example, Advanced Spaceborne Thermal Emission and Reflection Radiometer (ASTER), GeoEye, Pléiades, SPOT-5/6/7 (SPOT from French ‘Satellite pour l’Observation de la Terre’), Wordview-1/2) or radar (for example, Shuttle Radar Topography Mission (SRTM), TerraSAR-X add-on for Digital Elevation Measurements (TanDEM-X)) sensors and products. The spatial coverage of regional results from participants ranged between 25% and close to 100%. The observational coverage was considered to be representative of the entire region or data gaps were filled by spatial or hypsometric interpolation⁴⁶. DEM differencing often provides long-term regional trends at high confidence levels, but it does not fully represent seasonal or annual variability. Consequently, we combined the long-term trends from DEM differencing and the annual variability from glaciological observations.

Altimetry

Laser and radar altimetry determine elevation change (traditionally in the unit of metres) along ground tracks or in swath modes, which must be extrapolated to glacier-wide results and aggregated to regional estimates. Elevation change can be derived at seasonal to monthly resolution, often reported as multi-annual change rates, from laser altimetry (2003–2009 from ICESat, since 2018 from ICESat-2) and radar altimetry (since 2010 from CryoSat-2, earlier from ERS-1/2 and Envisat). Results are partly corrected for elastic uplift rates from present-day and long-term ice-mass changes (for example, in Greenland periphery, Iceland)⁶⁵ and require density assumptions for converting to geodetic mass changes²⁹. Similar to DEM differencing, altimetry represents glacier mass changes relevant to sea-level rise. We analysed 41 geodetic assessments from altimetry from nine research teams covering 13 out of 19 regions using various methods^{28,42,43,45,79,80,81,82,83,84,85} (Extended Data Fig. 1 and Supplementary Table 1). Altimetry provides both temporal variability and long-term trends at high confidence levels for regions with a large glacier area, including the Greenland and Antarctic periphery. The missing regions either have small and widely scattered glaciers or have not been covered by the mission planning. Like DEM differencing, the spatial coverage differed between regions and sensors used. It was either considered representative for the entire region or data gaps were filled by spatial or hypsometric interpolation^28,86,87,88.

Gravimetry

This approach estimates mass-change anomalies traditionally in the unit of gigatonnes (1 Gt = 10¹² kg) by measuring changes in the distance between two satellites in a shared orbit and by applying a series of corrections, for example, for atmospheric drag, solar radiation pressure, glacial isostatic adjustment, signal leakage and non-glacier hydrological components^26,30,31,89. The method has almost continuously provided regional mass changes at monthly resolution since 2002, with a few dozen months of missing data (typically interpolated from the months before and after) and an observational gap of 11 months between the GRACE (2002–2017) and GRACE Follow-On (2018 to present) missions. For gravimetry, we analysed 78 data contributions from 7 research teams, covering 17 out of 19 regions using various methods^{31,90,91,92,93,94,95,96,97} (Extended Data Fig. 1 and Supplementary Table 1). Gravimetry provides both temporal variability and long-term trends at medium to high confidence levels for seven regions with a large glacier area and related large mass change. The periphery of Greenland and Antarctica is excluded owing to the high uncertainty of separating the mass-change signal of the glaciers and the ice sheets. Gravimetry estimates for regions with a small glacier area and related small mass changes are considered to be of low to no confidence owing to the leakage of non-glacier mass changes, limitations in the hydrological models and poor signal-to-noise ratio and, hence, are shown in the results (Extended Data Table 2 and Extended Data Figs. 1, 3 and 4) for completeness but not included in our combined estimates. The challenges of isolating the glacier signal with GRACE and GRACE Follow-On in regions with a small glacier area are well reflected in implausible mean regional change rates or interannual variabilities shown in Extended Data Fig. 3.

Hybrid estimates

Some research teams provided estimates combining results from different observation methods, labelled ‘hybrid results’ here to distinguish them from the ‘combined results’ derived by the GlaMBIE workflow. We analysed 58 hybrid results from 7 research teams covering all 19 regions (Extended Data Fig. 1 and Supplementary Table 1). These hybrid estimates are diverse in their approaches. Dussaillant et al.^56,98 and Huss et al.²³ combined glaciological observations with geodetic estimates at the glacier scale for all 19 regions with similar but partly different approaches. From their results, we assigned the temporal variability to the glaciological and the long-term trends to the DEM differencing methods. Box et al.⁹⁹ similarly calibrated glaciological observations to results from gravimetry in Alaska, the Canadian Arctic, Iceland, Svalbard and the Russian Arctic. From their results, we assigned the temporal variability to the glaciological and the long-term trends to the gravimetric method. Colgan et al.¹⁰⁰ inverted low-resolution gravimetry changes over Greenland periphery and the Canadian Arctic using high-resolution altimetry observations. We used the results for the Canadian Arctic and assigned their long-term trends to gravimetry. Ke et al.¹⁰¹ calculated long-term trends from ICESat-2 with reference to SRTM and National Aeronautics and Space Administration’s Digital Elevation Model (NASADEM) over High Mountain Asia. We assigned their results to altimetry. Pálsson et al.¹⁰² submitted two versions of glaciological observations covering 90% of the glacier area over Iceland, one with and one without corrections for non-surface mass-change components. We used their results with corrections and assigned both their trend and variability to the glaciological method. Miles et al.¹⁰³ estimated glacier mass changes over High Mountain Asia in an approach combining DEM differencing, ice velocities and glacier thickness estimates. We excluded their results to avoid double counting the long-term trends from DEM differencing by Brun et al.⁶⁹, submitted to GlaMBIE separately.

The GlaMBIE workflow

The principal approach and workflow of the intercomparison exercise are illustrated in Extended Data Fig. 2 and described in the following paragraphs. In summary, we compiled glacier mass changes through an open call to the research community from the different observation methods at their native temporal resolution and in their traditional units for the 19 predefined regions. After primary quality control, input data were homogenized for time, space and unit domains and were selected based on an expert evaluation. Selected datasets were de-trended according to their annual variability and long-term trends. After re-trending, datasets were combined within and among observation methods.

Quality control, homogenization and selection

All data submissions were run through basic quality controls, including checks for completeness and correctness concerning data format, the plausibility of value ranges relating to units, potential outlier detection, and identification of spatial and temporal data gaps. A data-quality report with plots for visual inspection was generated for each data submission, and identified issues were discussed and resolved with the data provider. In the first processing step, all input data were homogenized concerning unit, temporal and spatial domains to reduce corresponding biases and to make results comparable across observational sources. Units were converted—if required—to specific mass changes (in metre water equivalent), considering time-variable glacier area as outlined above. Results from gravimetry (in gigatonnes) were divided by the regional glacier area, considering area changes over time. Results from altimetry and DEM differencing (in metres) were converted assuming an average density of the volume change of 850 kg m⁻³, assuming no change in bulk glacier density over the observation period. In line with the work by Huss²⁹, we prescribed the related uncertainty to be ±60 kg m⁻³ and chose to increase it to ±120 kg m⁻³, ±240 kg m⁻³ and ±480 kg m⁻³ for survey periods shorter than 10 years, 5 years and 1 year, respectively. We aligned the temporal domain to annual resolution following hydrological years in the regions of the Northern Hemisphere (1 October to 30 September), in the tropics (1 January to 31 December) and in the Southern Hemisphere (1 April to 31 March). Input data with monthly or seasonal resolution were aggregated to annual sums over the hydrological year. Input data with multi-annual resolutions, such as from DEM differencing or partly from altimetry and gravimetry, were used for long-term trends only, corrected to hydrological years (if needed) by assuming a linear change. Regional results were corrected from hydrological to calendar years for global aggregation using regional glaciological time series, which were downscaled from seasonal to monthly resolution using an analytical model approach¹⁰⁴. The uncertainty of this temporal correction was assumed to be ±10% of the correction, which depends on the seasonal mass turnover of the region¹⁰⁵. The spatial domain was regularized by using common glacier regions and (earlier) converting all results to specific mass changes (in metre water equivalent) under consideration of regional area changes. This approach allowed us to use common regional glacier area and area-change rates to calculate regional mass changes in gigatonnes across all input data.

After quality control and homogenization, all input data underwent an expert evaluation by the GlaMBIE community (that is, co-authors and data contributors). In a workshop, the consortium and representatives from all data contributors assessed the confidence levels¹⁰⁶ (no, medium or high) of both temporal variability and long-term trend of each observation method at a regional level. On the basis of this consensus decision, we excluded input data from observation methods regionally evaluated as having ‘no confidence’. We used input data of medium or high confidence with the same weight. Our combined regional estimates give equal weight to all selected input data within and among observation methods (that is, glaciological and DEM differences, altimetry, gravimetry). Within observation methods, this approach implicitly gives a larger weight to multiple results from the same sensors, that is, various results based on ASTER within DEM differencing, or numerous results based on the same GRACE or GRACE Follow-On gravity field solution within gravimetry. Among observation methods, the weight of a given method depends on the availability of regional data and the assessed confidence level. As an example, the glaciological observations have no weight on regional trends (owing to ‘no confidence’) but determine the temporal variability by one-third in Iceland (sharing the same weight with altimetry and gravimetry) and fully in Central Europe (owing to lack of confident results from the other methods). Altogether, our combined estimates reflect the currently available observations with a potential bias towards specific sensors and approaches. An overview of all included and excluded datasets is given in Extended Data Fig. 1 and Supplementary Figs. 1–19, and the regional weight of each observation method can be derived from Extended Data Fig. 3.

Separation of temporal variability from the long-term trend

We note that in the case of all time series covering the same observation period, one could simply average the annual values. For overlapping observation periods, however, simple averaging would introduce artefacts, that is, jumps from average values within the common observation period to observed values of one series outside the common observation period. In our approach, we first separate the annual anomalies from the period average and then calibrate each series with reference to a common period of records (cPoR)^25,52 (Extended Data Fig. 2a), which differs depending on region and method. We calculated for each time series (i) the annual anomaly β for a given year (y) as the difference between the observed mass change B and the arithmetic mean balance \(\barB\) over the common period of records:

The resulting time series of annual anomalies were then averaged to one time series of mean yearly anomalies \(\bar\beta _y\). This yearly time series was then re-trended by adding the long-term trend of each input dataset:

This resulted in multiple time series of calibrated annual mass changes \(B_\rmcal,i\) (one for each input dataset), which have different long-term trends (based on the input dataset) but a common estimate of annual anomaly. In cases without annual observations (for example, altimetry pre-2010 or gravimetry during the observational gap between GRACE and GRACE Follow-On), we used the averaged anomaly from the other observation methods to fill in \(\bar\beta _y\) for missing years. Finally, these calibrated yearly time series were averaged to get one time series \(\barB_\rmcal\) for each observation method and region.

The uncertainty of the mean annual anomaly \(\sigma _\bar\beta \) combines the reported observational uncertainty σ_obs of the individual input datasets (i) with the variability of the ensemble σ_var, taken as independent:

with

and

Thereby, the ensemble variability was expressed as standard error, which was calculated from the standard deviation (s.d.) of the annual values from the common period with full sample coverage (PoR) divided by the number of time series (N) for a given year (y).

The uncertainty of the calibrated time series was calculated by combining the uncertainties of the mean anomalies \(\bar\sigma _\bar\beta _y\) and the long-term trends \(\sigma _\barB_i\) as:

The uncertainty of the mean calibrated time series \(\sigma _\barB_\rmc\rma\rml\) combines (again) the uncertainties of the individual calibrated time series with the variability of the corresponding ensemble.

Combined estimate within observation methods

The approach of de-trending and re-trending was applied to combine the input data for each observation method. We combined the glaciological method’s temporal variability with the long-term trends from geodetic DEM differencing. We separately combined temporal variability and long-term trends from within the methods for altimetry and gravimetry. The expert evaluation assigned data submissions from hybrid approaches to the best-fitting method. As a result, for each region, our approach provided one combined estimate for (1) glaciological observations and DEM differencing, (2) altimetry and (3) gravimetry (Extended Data Fig. 2b), provided that corresponding data had been submitted. The uncertainties of the combined estimates were calculated, as explained in the section above.

Combined estimate among observation methods

On the basis of these (up to three) combined estimates per region, we then calculated a combined estimate among observation methods using the same approach as before. This means that we de-trended the time series with reference to the common observation period. Then, we averaged these anomalies and re-trended the time series of mean anomalies to the trends of the observation methods over the common period of records. Finally, we averaged the resulting time series to get a combined regional estimate among observation methods (Extended Data Fig. 2b). The regional results are provided as mean specific mass changes (B_reg in m w.e.) and as mass changes (ΔM_reg in Gt). The latter was calculated as the product of the specific mass changes and the regional glacier areas (S_reg), considering area changes (see above):

The corresponding uncertainty (σ_ΔM) was calculated by combining fractional uncertainties related to the combined observations (σ_B) and regional glacier area (σ_S):

Global aggregation

Global estimates were computed by aggregation of regional results, that is, by calculating regional area-weighted means for specific mass changes (B_glob in m w.e.), considering area changes (see above):

and by simple sums for global mass changes (ΔM_glob in Gt):

Related uncertainties were calculated, assuming that regional estimates are independent, as:

and

Observations from all methods represent glacier mass changes above sea level, or—to be more precise—above floatation level. Hence, the conversion to sea-level equivalents was directly calculated by dividing the global mass change (Gt) by an ocean area of 362.5 million square kilometres^107,108. These estimates include glacier mass changes in hydrologically landlocked (endorheic) basins, which only indirectly contribute to sea-level changes¹⁰⁹. We note that the uncertainties (σ) above are formulated at the 1σ level (that is, 68% confidence interval) to simplify equations, whereas the results in the main text, figures and tables are reported at the 1.96σ level (that is, 95% confidence interval).