Spontaneous ordering of identical materials into a triboelectric series

Contact electrification, also known as ‘tribocharging’ or ‘triboelectrification’, defies our understanding. In principle, it seems simple: take two neutral insulators, touch and separate them and they will exchange electrical charge^1,2,3. Often identified with ‘static electricity’ and demonstrations of balloons rubbed on hair, contact electrification is nevertheless essential in wide-ranging corners of nature, from the electrification of thunderclouds⁴, to the pollen that sticks to bumblebees⁵, to the accretion of dust into protoplanets⁶. Yet, as any contact electrification article reiterates, the most fundamental aspects of the effect, that is, the charge carrier(s) and the cause(s) for their exchange, remain debated. Among the most salient observations associated with contact electrification is the ‘tendency’ of different materials to order into triboelectric series, that is, transitive lists based on the sign with which materials charge^2,7,8,9,10. For example, in the first such list, created by J. C. Wilcke in 1757, glass charged positive to paper and paper charged positive to sulfur, ergo glass charged positive to sulfur². The notion of triboelectric series has prompted suggestions that contact electrification might be dominated by a single underlying parameter—for the sake of a name, call it φ. The slate of candidate mechanisms associated with φ is numerous, including: electronic properties^11,12, acidity/basicity^13,14,15, zeta potential^16,17, hydrophilicity/hydrophobicity^{18,19,20,21,22,23}, flexoelectricity²⁴ and mechanochemistry^{25,26,27,28,29,30,31}, to name a few. However, owing to the lack of consensus on the most basic aspects of contact electrification, there is no agreement that one, if any of these, is correct. Moreover, many experiments cast doubt on the validity of triboelectric series—and the hope for any rational explanation of contact electrification—all together^1,3. Series compared among different laboratories are frequently inconsistent^1,3,32. Two materials can initially exchange charge one way (A positive to B), only later to exhibit polarity reversal (B positive to A)^33,34. Experiments have occasionally pointed to the existence of ‘triboelectric cycles’, that is, series that loop back onto themselves^25,35,36. More perplexingly still, even ‘identical’ materials exchange charge when contacted^37,38,39, with one leading model for this effect relying on randomness and unpredictability⁴⁰.

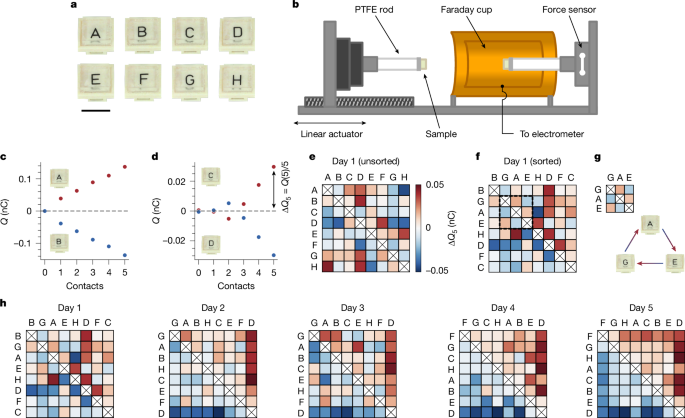
On the basis of the preceding discussion, our investigation begins with the following question: do samples of identical materials order into triboelectric series? We pursue this question with the system shown in Fig. 1. We prepare identical samples of polydimethylsiloxane (PDMS) and label them with letters A–H (Fig. 1a). We work with PDMS because of its low Young’s modulus (E = 4.3 ± 0.2 MPa; see Supplementary Information and Extended Data Fig. 1) and extreme smoothness (nominal roughness of pristine, that is, newly fabricated and uncontacted, samples R_q ≈ 7 Å), which help to make contacts as ‘conformal’ as possible. To measure charge exchange for a pair of samples, we use the setup shown in Fig. 1b. We mount each sample on a polytetrafluoroethylene (PTFE) rod. One rod is inside a Faraday cup that is connected to an electrometer, which allows us to measure charge (see Methods). The other is outside on a linear actuator that enables us to push the samples together. With an inline force sensor, we reach a set pressure (P ≈ 45 kPa, or approximately 1% macroscopic strain) in every contact. Before measuring charge exchange, samples are always fully discharged (<0.5 pC residual charge; see Methods). Representative charge-exchange data for consecutive contacts with two sample pairs are shown in Fig. 1c,d. In the first, one sample charges consistently positively and the other consistently negatively (Fig. 1c). In the second (Fig. 1d), the charging exhibits a polarity reversal—an observation seemingly indicative of the unpredictability of contact electrification but—as will become clear later—an important clue. To account for such variability, we define ΔQ₅ as the average charge exchange over five contacts, always starting with fully discharged samples (see Methods).

a, We prepare identical samples of PDMS by curing a single parent slab and then cutting eight smaller (1 cm × 1 cm × 0.3 cm) pieces, labelled A–H. Scale bar, 1 cm. b, We mount sample pairs on PTFE rods and use a linear actuator to push them together. Inline force feedback allows us to reach a set pressure (P ≈ 45 kPa, approximately 1% macroscopic strain). We measure charge exchange with an electrometer connected to a Faraday cup enclosing one sample. Before all measurements, samples are discharged to <0.5 pC (see Methods). The chamber/sample storage area is held at 30 ± 2% RH and 22 ± 1 °C. c, Example of charge versus contacts with two pristine samples, one charging persistently positively and the other negatively. d, Charge exchange between two pristine samples that exhibits an unpredictable sign change. To average over such variability, we define the average exchange after five contacts as ΔQ₅, which is always measured after both samples have been completely discharged. e, To test for a triboelectric series, we measure ΔQ₅ for all pair combinations with a staggered contact sequence (see Methods), creating a matrix in which the colours indicate charge given to the column sample. f, The inability to sort the matrix (see Methods) in e such that the upper-right (lower-left) corner is purely positive (negative) indicates that the samples charge randomly, that is, do not form a series. g, As highlighted in f, the defects in a series are indicative of cycles; here A charges positively to G, E charges positively to A, but E charges negatively to G. h, Repeating tests over several days with the same set of samples, randomness gives way to order and, by the fifth day, the samples form a perfect triboelectric series.

We test whether samples order into a series by measuring ΔQ₅ for all pair combinations (28 in total) in a staggered sequence (see Methods) and constructing a charge-exchange matrix, for which the colour represents the charge acquired by the column sample. Figure 1e shows such a matrix for a first attempt with pristine samples. The unsorted matrix, that is, with letters arranged alphabetically, is almost completely random, but this is to be expected. The likelihood of any order corresponding to our alphabetical naming is very small: 1/2²⁸ if samples charge completely random, 1/8! if they form an unknown series. When we sort the samples according to the number of positive and negative outcomes (Fig. 1f; see Methods), they still exhibit highly random charging—the columns and rows cannot be arranged such that all entries above (below) the diagonal are positive (negative), as required for a series. On closer inspection, the imperfections are indicative of the triboelectric cycles mentioned previously. For instance, as highlighted in Fig. 1g, sample A charges positive to G, E charges positive to A and yet E charges negative to G. Such paradoxes are not because of remnant charge (as ΔQ₅ is always measured after complete discharge) nor to experimental uncertainty (as measurement error is much smaller than any ΔQ₅ value).

Once again, these data seem to highlight the unpredictability of contact electrification and in particular the role of randomness with ‘identical’ materials. An optimistic spin on the chaos is that it could offer a starting point from which one might alter parameters one at a time until order appears. To our surprise, however, we need not intentionally alter anything. In Fig. 1h, we show the resulting sorted charging matrices obtained by simply repeating the measurements of Fig. 1e with the same samples on consecutive days. The initial randomness progressively dissipates, giving way to a perfect series on the fifth attempt. This spontaneous ordering occurs every time we start with a pristine ensemble. Typically, we observe a perfect series around the fifth attempt, although it has required as many as ten and as few as two. Once a series forms, it is relatively stable, but cycles or letter swaps (especially in the centre) may pop in and out.

What causes this evolution? One possibility is that some parameter changes with time, altering the charging behaviour of samples with it. For instance, PDMS is known to exhibit ageing, in which, over a timescale of weeks to months, the mechanical⁴¹ and electrical properties⁴² can drift. More generally, contact electrification has been shown to be extremely sensitive to environmental conditions²³, for example, relative humidity (RH) history, which might also be considered. We can exclude such time-based evolution for the following reasons. First, pristine samples begin by charging randomly and evolve into a series independently of when we test them (for example, a day, a week, a month) after their fabrication. Second, although large variations in humidity history (>90% RH) do alter the observed charging behaviour (see Supplementary Information and Extended Data Fig. 2), we store samples and conduct experiments in tightly regulated conditions with little variability (see Methods).

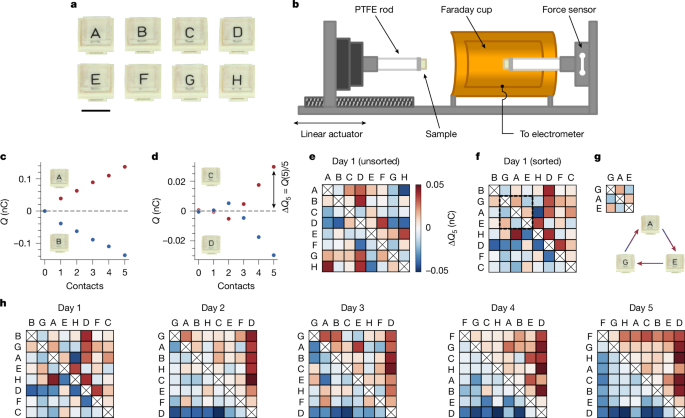
Rather than time, we find that the evolution is a result of the act of contact. Figure 2a shows measurements of ΔQ₅ for 24 pairs of pristine samples. These charge randomly around zero, with a spread of about 0.007 nC. To isolate contact as the culprit, we compare this baseline to experiments with a new batch of pristine samples, half of which we expose to 100 previous contacts (and, as always, discharge). When we measure ΔQ₅ for the ‘contact-biased’ samples pressed against the uncontacted ones (Fig. 2b), we see a substantial effect. The contacted samples always charge negatively. The 100 contacts used to cause this are well within the total number required for a series to emerge (about 5 trials × 7 samples × 5 contacts = 175 contacts). We investigate this further using a trio of samples, as shown in Fig. 2c: an ‘advancing’ sample (green A), a ‘lagging’ sample (ivory A) and an ‘extra’ sample (ivory X). Starting from the pristine state, we first measure ΔQ₅ between the advancing and lagging samples. We then bias the advancing sample with 20 contacts against the extra sample. After discharging, we measure ΔQ₅ again between advancing and lagging samples. By repeating this process, we generate a growing difference in the contact history between the advancing and lagging samples. This translates into the advancing samples charging increasingly negative, with different rates and plateaus for different trios (Fig. 2d). As we show in the Supplementary Information and Extended Data Fig. 3, the bias created by contact is long-lasting. The act of contact—by definition required for contact electrification to occur—can alter the underlying parameters(s) that drive contact electrification. In other words, our materials ‘remember’ their contact history.

a, Towards uncovering what causes the series evolution, we first performed baseline measurements between 24 pairs of pristine samples. These charge randomly about zero with a standard deviation of about 0.007 nC. b, Motivated by the possibility that the act of contact itself could drive the series evolution, we prepare 48 new samples and expose half to 100 prior contacts. Contacting these against unbiased ones and measuring ΔQ₅ reveals a marked effect, with the previously contacted samples always charging negative. c, We investigate how this ‘contact bias’ evolves using trios of samples: an ‘advancing’ sample (green A), a ‘lagging’ sample (ivory A) and an ‘extra’ sample (ivory X). We first measure ΔQ₅ between the advancing and lagging samples starting from the pristine state. We then subject the advancing sample to 20 contacts with the extra sample. After discharging, we measure ΔQ₅ again between the advancing and lagging samples. Repeating this process develops a growing contact bias between the lagging and advancing samples. d, Charge exchange versus advancing (bottom) and lagging (top) contacts for different trios of samples. All advancing samples charge more negatively as their contact bias increases, although each one at a different rate and with a different plateau. As explained in the main text, we assume that the charge exchange in this evolution is caused by a difference in a generalized potential, φ, which obeys equation (2). Solid curves are fits to the model.

This reality suggests a hypothesis to explain the spontaneous ordering into a series. First, we suppose that every sample, i, has some ‘effective potential’—for the sake of a name, call it φ_i. In line with the randomness-based model for identical materials⁴⁰, their initial values come from some parent distribution, \({\varphi }_{i}^{0}\approx {\mathcal{N}}({\varphi }^{0},{\sigma }_{0})\), which could be, for example, Gaussian^22,40,43. When two samples, i and j, make contact, the charge they exchange is related to the difference in their potentials, that is,

In this picture, the ordering of the triboelectric series at any instant should correspond to the ordering of the different potentials. However, it is clear from Fig. 2d that contact causes changes to the potentials, that is, dφ_i/dn_i = f(n_i, φ_i,…), in which n_i is the number of contacts sample i has experienced. The critical idea is now this: if contact causes the potentials to ultimately separate, then any ensemble will eventually result in a triboelectric series. Moreover, if the ordering of the final potentials, \({\varphi }_{i}^{\infty }\), is not the same as \({\varphi }_{i}^{0}\), it must be the case that, during their evolution, they ‘crossed’, resulting in what we (incorrectly) perceive as ‘cycles’.

We can use this hypothesis to develop a numerical model that reproduces our experimental data. Figure 2d implies an evolution consistent with the following differential equation,

in which α_i are growth rates and \({\varphi }_{i}^{\infty }\) are the values of the potentials at infinite contacts.

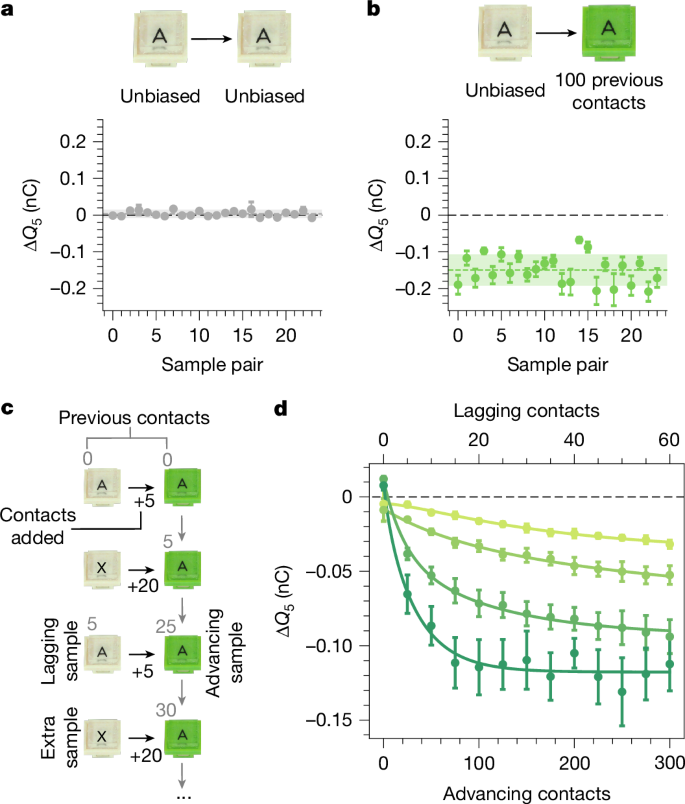
We use this equation to fit our data in Fig. 2d, which allows us to extract the ranges of the parameters α_i, \({\varphi }_{i}^{0}\) and \({\varphi }_{i}^{\infty }\). We use this information to draw new values of \({\varphi }_{i}^{0}\), \({\varphi }_{i}^{\infty }\) and α_i and define eight ‘virtual’ samples. We perform ‘contacts’ between these samples in a staggered sequence, just as in the experiments (see Methods), calculating the charge exchange through equation (1) and letting the φ_i evolve according to equation (2). Figure 3a shows the evolution of the φ_i versus the total number of contacts of all samples for a simulation instance. When a sample is being contacted, its potential evolves, and otherwise it is stationary. Owing to the fact that the samples evolve differently, the potentials cross each other. As foreseen in the previous paragraph, triboelectric cycles are manifestations of these crossings—they are not ‘real’ but rather consequences of our inability to perform contact without changing the system. This is the clue hidden in Fig. 1d, in which we witness a crossing in the act. As the samples continue to evolve, the individual φ_i slowly separate, until they are sufficiently resolved and no more crossings occur—the series is established. The corresponding matrices can be seen in Fig. 3b, in which—after five runs—a perfect series is attained. Just as in the experiments, the speed of this evolution depends on the values picked for the model, with slower or faster evolutions possible in different simulation instances.

a, Using equations (1) and (2), we perform numerical simulations to reproduce the series observed in Fig. 1. We initiate eight virtual samples with parameters α_i, \({\varphi }_{i}^{0}\) and \({\varphi }_{i}^{\infty }\), drawn from the range of fit values to the data in Fig. 2d. Performing the same staggered contact sequence as in Fig. 1e, we evolve and record all φ_i(n_i). We plot the total number of contacts, \(N=\sum {n}_{i}\), on the x axis and remove ensemble drift on the y axis by subtracting ⟨φ⟩. Individual φ_i swap positions during the evolution but stably separate after a sufficient number of contacts. b, Corresponding charging matrices from a, for which we observe samples evolve into a series such as in the experiments. The apparent disorder in imperfect matrices, that is, the appearance of ‘cycles’, is because of the φ-crossings between samples as contact causes them to evolve. c, We develop an algorithm to force experiments to produce the ‘appearance’ of a series of our choosing, in this case {A, B, C, D, E, F, G, H}. First, sample A is subjected to 50 contacts with an extra sample X, then five contacts with H, G, F, E, D, C to measure ΔQ₅, and finally 50 contacts with sample B (measuring ΔQ₅ in the first five). Next, sample B has five contacts with H, G, F, E, D and then 50 with C and so on. d, As intended, this creates the appearance of an alphabetical series on the first attempt. As we show in Extended Data Fig. 5, this is indeed only an appearance, as reattempting the series with a staggered contact sequence (the one used for Fig. 1e) leads to a different and unpredictable result.

The proposed model not only allows us to explain previous observations but also predict new ones. To illustrate this, we design an experimental ‘contact algorithm’ to create the appearance of the series of our choosing (Fig. 3c). We again fabricate eight pristine samples A–H, plus an extra sample X. As a first step in our algorithm, we use the extra sample to bias A with 50 contacts. We then measure ΔQ₅ for A against the rest of the samples from H to C. With sample B, we perform 50 contacts against A, which simultaneously allows us to bias sample B while measuring its ΔQ₅. Next, we measure ΔQ₅ for B against all other samples except C, with which we perform 50 contacts while measuring ΔQ₅, and so on. As we remarked earlier, the probability that eight pristine samples order into an alphabetical series is very small (1/8! at best). Figure 3d shows that, by understanding and wielding the role of contact history, we create this motif on the first attempt. In the Supplementary Information and Extended Data Fig. 4, we illustrate that we can just as well force the appearance of a cycle by manipulating contact history. In either case, the word ‘appearance’ is key, as we are enforcing outcomes by always ensuring that one sample has substantially more contacts than the other when ΔQ₅ is measured. As we show in the Supplementary Information and Extended Data Fig. 5, reusing the samples of Fig. 3d for a second try at a series without manipulating the contact order (that is, with the same staggered contact sequence as Fig. 1e) leads to an entirely different and (predictably) unpredictable result, including ‘cycles’.

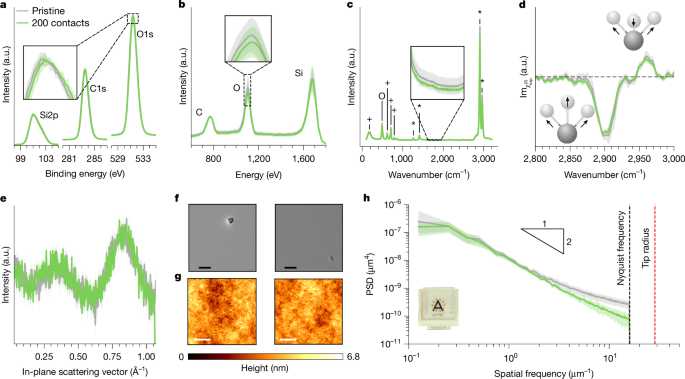
Clearly, the act of contact fundamentally alters sample surfaces in a way that affects the contact electrification mechanism. These alterations could be elemental (for example, changing the atomic composition), molecular (affecting bonds) or physical (for example, changing structure/morphology). In Fig. 4, we present a set of surface-sensitive tests to search for these changes. At the atomic scale, experiments for contact electrification between different materials have shown that contact leads to changes in elemental composition^26,33,44. Figure 4a shows high-resolution X-ray photoelectron spectroscopy (HR-XPS) data for pristine versus 200-contacted samples, which reveal no statistically significant differences in the silicon, carbon or oxygen content. Increasing surface specificity with low-energy ion scattering (LEIS, which probes the first few atomic layers compared with about 10 nm in XPS) also shows no alterations (Fig. 4b). Some studies have reported molecular modifications after different-material contact electrification^26,30. We use Raman (to probe about 1 μm into the bulk) and heterodyne-detected sum-frequency generation (HD-SFG) spectroscopy (which probes the topmost roughly 1 nm) and, in both cases, cannot distinguish between pristine/contacted samples (Fig. 4c,d). To test for physical changes, we put three techniques to work: grazing-incidence X-ray scattering (GIXS), scanning electron microscopy (SEM) and atomic force microscopy (AFM). In-plane signals from the GIXS measurements show that there are no detectable differences in the subnanometre, interatomic arrangements near the surface (Fig. 4e). At first glance, the SEM and AFM images (Fig. 4f,g) seem to indicate no obvious morphological differences on the surface. However, calculating the power spectral density (PSD) of the AFM data (Fig. 4h) reveals a surprising feature—contacted surfaces are smoother at higher spatial frequencies. Performing many scans at several locations on the same sample before/after contact, we find that these differences are statistically significant. In the Supplementary Information and Extended Data Figs. 6–8, we show that increasing from 200 contacts to several thousand creates no changes in the LEIS, Raman and HD-SFG data but causes even more smoothening of the high-frequency tails in the roughness PSD. In Extended Data Fig. 9, we contact pristine samples against intentionally roughened ones, in which again the smooth ones charge negatively. These observations strongly suggest that the high-frequency smoothening presented in Fig. 4h is indeed the cause of the contact bias in Fig. 2 and, consequently, the driver of the spontaneous ordering in our system.

a, To probe atomic differences in the uppermost approximately 10 nm, we use HR-XPS and measure the Si2p, C1s and O1s peaks. Previous work⁴⁴ reported a subtle (about 300 meV) shift in the O1s peak of PDMS after contact electrification with polyvinyl chloride (PVC), but averaging several measurements shows that such shifts are within noise in our experiments (that is, shaded error band in the inset). b, Focusing on elemental differences in the outermost atomic layers with LEIS again shows no measurable differences in the C, O or Si concentrations. c, To probe for molecular differences, we record Raman spectra at several locations and plot the mean (line) and standard deviation (error band). The peaks marked as +, O and * correspond to Si–C, Si–O and C–H, respectively. We observe no notable differences in any of the peaks, nor can we reproduce differences found previously³⁰ between 1,600 and 1,950 cm⁻¹ and attributed to COOH groups (inset). d, To probe the outermost molecular layer, we use HD-SFG to measure the symmetric/asymmetric C–H stretching modes (2,900 cm⁻¹ and 2,960 cm⁻¹, respectively). Within the error bands, the pristine/contacted samples are again indistinguishable. e, GIXS data for pristine and contacted samples, which probes subnanometre interatomic structure, also renders pristine/contacted samples as indistinguishable. f, Using SEM to image each surface, we find no visible changes in the surface integrity; regions with (rare) specks are shown intentionally to aid visualization. Scale bars, 20 μm. g, With AFM to characterize surface roughness, we do not find any visible differences. Scale bars, 2 μm. h, However, we do detect differences in the PSD of the roughness, for which contacted samples are smoother at higher spatial frequencies than uncontacted ones. The error bands represent scatter from about ten measurements on different regions for the same sample in the pristine/contacted states, indicating that this result is statistically significant. a.u., arbitrary units.

As we discuss thoroughly in the Supplementary Information, a long history of observations casts suspicion on mechanical history and surface morphology, yet have not cleanly established that every charge-exchanging contact probably entangles the two. Most notably, recent experiments have shown the tendency that ‘smooth polymers charge negatively’ is widespread²⁹. Taking this at face value, the only conceptual leap required for the spontaneous ordering of series to be widespread is the occurrence of morphological alterations during contact, which is a well-established principle in the tribological framework of Bowden and Tabor⁴⁵. These facts lead us to conjecture frequent occurrence in other polymers, although further experiments are required to know for certain. For other insulators beyond polymers (for example, insulating oxides), we do not extend our conjecture.

We conclude that the unpredictability in contact electrification may not be so hopeless after all. By carefully paying attention to contact history, we can not only explain the unpredictability in our system but even tame it. Considering the effect of contact history, the notion of triboelectric series may be a useful heuristic, but not much more. If the effect is widespread, chasing an immutable ordering is comparable with chasing a mirage. Last, by focusing on contact electrification with identical materials, and particular sources of unpredictability therein, we distil minimal ingredients relevant to its mechanism(s). With a phenomenon that is (1) so unpredictable and (2) studied by distinct scientific disciplines with different languages and conceptual biases, such purified information is valuable. In our system, it allows us to conclude that the cause of charge transfer must be intimately connected to nanoscale contact mechanics. In light of this, two of the mechanisms from the introduction deserve special attention: mechanochemistry and flexoelectricity. The former proposes that mechanical strain—which becomes exceptionally large during deformation of nanoscale asperities—can be sufficient to cause heterolytic bond cleavage and consequent liberation of charged species for transfer^25,29,30. The latter couples electrical polarization to mechanical strain gradients—which also become large in nanoscale deformation—and hence can be expected to produce large electric fields during contact⁴⁶. Our data are insufficient to validate/invalidate either of these hypotheses directly but compel us towards enticing speculation: both may be at play. Our work therefore calls for more careful consideration of these mechanisms, potentially in cooperation, with a special focus on the inherently tribological nature of contact electrification.