Learning produces an orthogonalized state machine in the hippocampus

All procedures were performed in accordance with the Janelia Research Campus Institutional Animal Care and Use Committee guidelines. Both male and female GCaMP6f (Thy1-GCaMP6f⁵⁹) transgenic mice were used, 3–6 months of age at the time of surgery (3–8 months of age at the beginning of imaging studies).

Surgery

Mice were anaesthetized with 1.5–2.0% isoflurane. A craniotomy on the right hemisphere was performed, centred at 1.8 mm anteroposterior and 2.0 mm mediolateral from the bregma using a 3-mm diameter trephine drill bit. The overlying cortex of the dorsal hippocampus was then gently aspirated with a 25-gauge blunt-tip needle under cold saline. A 3-mm glass coverslip previously attached to a stainless-steel cannula using optical glue was implanted over the dorsal CA1 region. The upper part of the cannula and a custom titanium headbar were finally secured to the skull with dental cement. Mice were allowed to recover for a minimum of 2 days before being put under water restriction (1.0–1.5 ml daily), in a reversed dark–light cycle room (12-h light–dark cycle).

Behaviour

Virtual reality setup

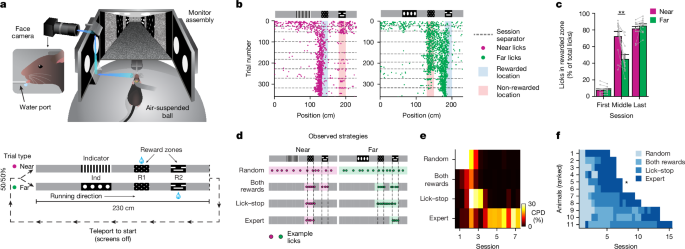
The virtual reality behavioural setup was based on a design previously described⁶⁰. The spherical treadmill consisted of a hollowed-out Styrofoam ball (diameter of 16 inches, 65 g) air-suspended on a bed of 10 air-cushioned ping-pong balls in an acrylic frame. Mice were head fixed on top of the treadmill using a motorized holder (Zaber T-RSW60A; MOG-130-10 and MOZ-200-25, Optics Focus) with their eyes approximately 20 mm above the surface. To translate the movement of the treadmill into virtual reality, two cameras separated at 90° were focused on 4-mm² regions of the equator of the ball under infrared light⁶⁰. Three axis movement of the ball was captured by comparing the movement between consecutive frames at 4 kHz and readout at 200 Hz (ref. ⁶⁰). A stainless-steel tube (inner diameter of 0.046 inches), attached to a three-axis motorized stage assembly (Zaber NA11B30-T4A-MC03, TSB28E14, LSA25A-T4A and X-MCB2-KX15B), was positioned in front of the mouse’s mouth for delivery of water rewards. The mouse was shown a perspective corrected view of the virtual reality environment through three screens (LG LP097QX1 with Adafruit Qualia bare driver board) placed roughly 13 cm away from the animal (Fig. 1a). This screen assembly could be swivelled into position using a fixed support beam. All rendering, task logic and logging were handled by a custom software package called Gimbl (https://github.com/winnubstj/Gimbl) for the Unity game engine (https://unity.com/). All inter-device communication was handled by a MQTT messaging broker hosted on the virtual reality computer. Synchronization of the virtual reality state with the calcium imaging was achieved by overlaying the frame trigger signal of the microscope with timing information from inbuild Unity frame event functions.

To observe the mouse during the task without blocking its field of view, we integrated a periscope design into the monitor assembly. Crucially, this included a 45° hot-mirror mounted at the base of a side monitor that passed through visible light but reflected infrared light (Edmund Optics 62-630). A camera (Flea3-FL3-U3-13Y3M) aimed at a secondary mirror on top of the monitor assembly could hereby image a clear side view of the face of the mouse. Using this camera, a custom Bonsai script⁶¹ monitored the area around the tip of the lick port and detected licks of the mouse in real time that were used in the virtual reality task as described below.

Head fixation training

After recovering from surgery, mice were placed on water restriction (1.0–1.5 ml daily) for at least 2 weeks before behavioural training. Body weight and overall health indicators were checked every day to ensure mice remained healthy during the training process. Mice were acclimated to experimenter handling for 3 days by hand delivering water using a syringe. For the next three sessions, with the virtual reality screens turned off, mice were head fixed on the spherical treadmill while water was randomly dispensed from the lick port (10 ± 3 s interval; 5 µl per reward). These sessions lasted until mice acquired their daily allotment of water or until 1 h had passed. We observed that during this period most mice started to run on their own volition. Next, we linked water rewards to bouts of persistent running and increased this duration across sessions till the mouse would run for at least 2 s straight (approximately five sessions). During this time, we also slowly increased the height of the animal with respect to the treadmill surface across sessions to improve performance. Mice that did not show sufficient running behaviour to acquire their daily allotment of water were discarded in further experiments.

2ACDC task

At the beginning of each trial, mice were placed at the start of a virtual 230-cm corridor. The appearance of the walls was uniform except at the location of three visual cues that represented the indicator cue (40 cm long) and the two reward cues (near or far; 20 cm long). Depending on the trial type, a water reward (5 µl) could be obtained at either the near or far reward cue (near and far reward trials). The only visual signifier for the current trial type was the identity of the indicator cue at the start of the corridor. For the first 2–3 sessions, the mouse only had to run past the correct reward cue to trigger reward delivery (‘guided’ sessions). On all subsequent sessions, mice had to lick at the correct reward cue (‘operant’ sessions). No penalty was given for licking at the incorrect reward cue. In other words, if the mouse licked at the near reward cue during a far trial type, then the mouse could still receive a reward at the later far reward cue. Upon reaching the end of the corridor, the virtual reality screen would slowly dim to black, and mice would be teleported to the start of the corridor to begin the next semi-randomly chosen trial with a 2-s duration. The probability of each trial type was 50%, but to prevent bias formation caused by very long stretches of the same trial type, sets of near or far trials were interleaved with their number of repeats set by a random limited Poisson sampling (lambda = 0.7, max repeats = 3). The identity of the indicator cue was kept hidden for the first 20 cm of the trial and was rendered when the mice passed the 20-cm position. To internally track the learning progress of the mouse, we utilized a binarized accuracy score for each trial depending on whether the mouse only licked at the correct reward cue. Once the mouse had three sessions in which the average accuracy was above 75%, we considered the mouse to have learned that cue pair.

2ACDC task with novel indicators

For 3 mice out of the 11 well-trained mice on the original 2ACDC task, we subsequently trained them to perform the 2ACDC task novel indicator pairs. After reaching three consecutive sessions with more than 75% task accuracy for the original 2ACDC task, the novel task was introduced in the following session, but with the original task shown for the first 5–10 min at the beginning of each session before switching completely to the new task. When the mouse could perform the new task for 3 consecutive days with more than 75% accuracy, we moved on to the next novel indicator pair until the last one was finished (four novel indicator pairs in total).

2ACDC task with extended grey regions

As another modification to the original task design, the grey regions were extended in certain trials, which we called the ‘stretched trials’. In the stretched trials, the linear track was extended from 230 cm to 330 cm, and the reward positions were moved from [130, 150] cm to [180, 200] cm (the first rewarding (near) object), and [180, 200] cm to [280, 300] cm (the second rewarding (far) object). Note that the distance between the indicator cue and the near object in the stretch trial is equal to the one between the indicator cues and the far object in the normal trial. During a session with stretch trials, following a 5-min warm-up using only the normal 2ACDC trial, the stretch trial was adopted at intervals of every five or six trials.

Calcium imaging

Neural activity was recorded using a custom-made two-photon random access (2P-RAM) mesoscope²⁷ and data acquired through ScanImage software⁶², running on MATLAB 2021a. GCaMP6f was excited at 920 nm (Chameleon Ultra II, Coherent). Three adjacent regions of interest (each 650 µm wide) were used to image dorsal CA1 neurons. The size of the regions of interest was adjusted to ensure a scanning frequency at 10 Hz. Calcium imaging data were saved into tiff files and were processed using the Suite2p toolbox (https://www.suite2p.org/). This included motion correction, cell regions of interest, neuropil correction and spike deconvolution as described elsewhere⁶³.

Multiday alignment

To image the same cells across subsequent days, we utilized a combination of mechanical, optical and computational alignment steps (Extended Data Figs. 2 and 3). First, mice were head fixed using a motorized head bar holder (see above), allowing precise control along three axes (roll, pitch and height) with submicron precision. Coordinates were carefully chosen at the start of training to allow for unimpeded animal movement and reused across subsequent sessions. The 2P-RAM microscope was mounted on a motorized gantry, allowing for an additional three axis of alignment (anterior–posterior, medial–lateral and roll). Next, we utilized an optical alignment procedure consisting of a ‘guide’ LED light that was projected through the imaging path, reflected off the cannula cover glass and picked up by a separate CCD camera (Extended Data Fig. 2b). Using fine movement of both the microscope and the head bar, the location of the resulting intensity spot on the camera sensor could be used to ensure exact parallel alignment of the imaging plane with respect to the cover glass.

To correct for smaller shifts in the brain tissue across multiple sessions, we took a high-resolution reference z-stack at the start of the first imaging session (25 μm total, 1-μm interval; Extended Data Fig. 2c). The imaging plane on each subsequent session was then compared with this reference stack by calculating a cross-correlation in the frequency domain for each imaging stripe along all depth positions. By adjusting the scanning parameters on the remote focusing unit of the 2P-RAM microscope, we finely adjusted the tip or tilt angles of the imaging plane to achieve optimal alignment with the reference stack. We used a custom online Z-correction module (developed by Marius Pachitariu⁶⁴, now in ScanImage), to correct for z and xy drift online during the recording within each session, using a newly acquired z-stack for that specific session.

To find cells that could be consistently imaged across sessions, we first performed a post-hoc, non-rigid, image registration step using an averaged image of each imaging session (diffeomorphic demon registration; Python image registration toolkit) to remove smaller local deformations (Extended Data Fig. 2g–i). Next, we performed hierarchical clustering of detected cells across all sessions (Jaccard distance; Extended Data Fig. 3). Only putative cells that were detected in 50% of the imaging sessions were included for further consideration. We then generated a template consensus mask for each cell based on pixels that were associated with this cell on at least 50% of the sessions. These template masks were then backwards transformed to the spatial reference space of each imaging session to extract fluorescence traces using Suite2p.

Data analysis

Coefficient of partial determination

To assess the unique contribution of each behavioural strategy (random licking, licking in both reward locations, lick–stop and expert) to overall animal behaviour, we used the coefficient of partial determination (CPD). In this analysis, a multivariable linear regression model was first fitted using all behavioural strategies as regressors, providing the sum of squares error (SSE) of the full model (SSE_fullmodel). Each regressor was then sequentially removed, the model refitted, and the SSE without that regressor (SSE_~i) was computed. The CPD for each regressor, denoted as CPD_i, was then calculated as CPD_i = (SSE_~i − SSE_fullmodel)/SSE_~i, revealing the unique contribution of each behavioural strategy to the overall variance in licking behaviour.

Place field detection

To identify significant place cells, we utilized an approach based on Dombeck et al.⁶⁵ (but see also Grijseels et al.⁶⁶ for overall caveats with such approaches). Place fields were determined during active trials, indicated by active licking within reward zones, and at running speeds greater than 5 cm s⁻¹. For detecting activity changes related to position, we first calculated the calcium signal by subtracting the fluorescence of each cell mask with the activity in the surrounding neuropil using Suite2p. Next, the baseline fluorescence activity for each cell was calculated by first applying Gaussian filter (5 s) followed by calculating the rolling max of the rolling min (‘maximin’ filter; see Suite2p documentation). This baseline fluorescence activity (F₀) was used to calculate the differential fluorescence (ΔF/F₀), defined as the difference between fluorescent and baseline activity divided by F₀. Next, we identified the significant calcium transient event in each trace as events that started when fluorescence deviated 5σ from baseline and ended when it returned to within 1σ of baseline. Here baseline σ was calculated by binning the fluorescent trace in short periods of 5 s and considering only frames with fluorescence in the lower 25th percentile.

Initially, putative place fields were identified by spatially binning the resulting ΔF/F₀ activity (bin size of 5 cm) as continuous regions where all ΔF/F₀ values exceeded 25% of the difference between the peak of the trial and the baseline 25th percentile ΔF/F₀ values. We imposed additional criteria: the field width should be between 15 and 120 cm in virtual reality, the average ΔF/F₀ inside the field should be at least four times greater than outside; and significant calcium transients should occur at least 20% of the time when the mouse was active within the field (see above). To verify that these putative place fields were not caused by spurious activity, we calculated a shuffled bootstrap distribution for each cell. Here we shuffled blocks of 10-s calcium activity with respect to the position of the mouse and repeated the same analysis procedure described above. By repeating this process 1,000 times per cell, we considered a cell to have a significant place field if putative place fields were detected in less than 5% of the shuffles.

Population vector analysis

For the analysis of similarity of representation between near versus far trial types, we performed population vector correlation on the fluorescence ΔF/F₀ data. Each 5-cm spatial bin, we defined the population vector as the mean ΔF/F₀ value for all neurons. Fluorescence data were included only when the speed of the mouse exceeded 5 cm s⁻¹. The cross-correlation matrix was generated by calculating the Pearson correlation coefficient between all location pairs across the two trial types.

Spatial dispersion index

To evaluate the extent of spatial dispersion in place tuning across single cells, such as distinguishing between tuning to single positions versus multiple positions, we took the single-cell tuning curve over track positions and normalized it so that the area under the curve is 1. The spatial dispersion index is defined as the entropy of this normalized ΔF/F₀ signal by: entropy = −∑ [p(i) × log₂ p(i)], where p(i) denotes the probability associated with each position bin index.

UMAP

To visually interpret the dynamics of high-dimensional neural activity during learning, we utilized UMAP on our deconvolved calcium imaging data. The UMAP model was parameterized with 100 nearest neighbours, three components for a three-dimensional representation, and a minimum distance of 0.1. The ‘correlation’ metric was used for distance calculation. The data, a multidimensional array representing the activity of thousands of cells concatenated from several imaging sessions, were fitted into a single UMAP model. This resulted in a three-dimensional embedding, in which each point characterized the activity of the neuron ensemble at a single imaging frame.

Modelling

CSCG

In the 2ACDC task, the combination of position along the track and trial type defines a state of the world (z). Although this state is not directly observable to the animal, it influences the sensory observation (x) that the animal perceives. The sequence of states in the environment obeys the Markovian property, in which the probability distribution of the next state (that is, the next position and trial type) depends only on the current state, and not all the previous states, assuming the animal always travels at a fixed speed. When an animal learns the structure of the environment and builds a map, it tries to learn which states (position, trial type) are followed by which states, and what sensory experience they generate. This can be viewed as a Markov learning problem. A HMM consists of a transition matrix whose elements constitute \(p(z_n+1| z_n)\) that is, the probability of going from state z_n at time n to z_n+1 at time n + 1, an emission matrix whose elements constitute \(p(x_n|z_n)\), that is, the probability of observing x_n when the hidden state is z_n, and the initial probabilities of being in a particular hidden state \(p(z_1)\).

The CSCG is an HMM with a structured emission matrix in which multiple hidden states, referred to as clones, deterministically map to the same observation. In other words, \(p(x_n=j|z_n=i)=0\) if \(i\notin C(j)\) and \(p(x_n=j|z_n=i)=1\) if \(i\in C(j)\), where \(C(j)\) refers to the clones of observation j²¹ (Extended Data Fig. 8f). The emission matrix is fixed and the CSCG learns the task structure by only modifying the transition probabilities (Extended Data Fig. 8e,f), making the learning process more efficient. The Baum–Welch expectation maximization algorithm was used to update the transition probabilities such that it maximizes the probability of observing a given sequence of sensory observations^67,68,69.

We trained the CSCG on sequences of discrete sensory symbols mimicking the sequence of patterns shown to the mice in the two tracks. Each 10-cm segment of the track was represented by a single sensory symbol. In addition, the teleportation region was represented by a distinct symbol repeated three times, spanning 30 cm. In the rewarded region, the mice could receive both visual input and a water reward simultaneously. However, our model could only process a single discrete stimulus at a time. Thus, we divided the rewarded region into two parts. We presented the visual cue first, mimicking the ability of the mouse to see the rewarded region ahead before reaching it. Subsequently, we presented a symbol representing the water stimulus, which was shared across the two trials. The near trial sequence, denoted as [1,1,1,1,1,1,2,2,2,2,1,1,1,4,6,1,1,1,5,5,1,1,7,0,0,0], and the far trial sequence, denoted as [1,1,1,1,1,1,3,3,3,3,1,1,1,4,4,1,1,1,5,6,1,1,7,0,0,0]′, were used. Where 1 represented the grey regions, 2 and 3 indicated the indicators for near and far tracks, respectively, 4 denoted the visual observation associated with the first reward zone, 5 represented the visual stimulus associated with the far reward zone, 6 denoted the common water reward received in both tracks, 7 represented the brick wall at the end of each trial, and 0 indicated the teleportation region (Extended Data Fig. 8c). However, the representations and learning dynamics are not sensitive to the addition of the brick wall and teleportation segments.

We initialized the model with 100 clones for each sensory observation symbol and performed 20 iterations of the expectation-maximization process at each training step with sequences from 20 randomly selected trials, comprising both near and far trial types. We extracted the transition matrix at different stages of learning and used the Viterbi training algorithm to refine the solution²¹, and then plotted the transition matrix as a graph, showing only the clones that were used in the representation of the two trials (Extended Data Fig. 8a). We ran multiple simulations and compared how correlation between the two trial types changed over learning for different positions along the track (Extended Data Fig. 8b).

We also explored alternate sequences of sensory stimuli. In one variant, we provided the water symbol before the visual symbol of the reward zone (for example, […1,1,1,6,4,1,1,1…] where 6 represented the water and 4 denoted the visual symbol). In addition, we introduced a symbol that conjunctively encoded the simultaneous water reward and visual symbol (for example, […111,4,6,111…] in the near trial and […111,5,8,111…] in the far trial, where 6 denoted a combined code for water and visual R1, and 8 represented a combined code for water and visual R2; Extended Data Fig. 8c). Although the final learned transition graphs matched for all the four sequence variants, the exact sequence of learning differed. Specifically, reward cue followed by a visual cue for reward zone often led to decorrelation of pre-R1 followed by pre-R2 (Extended Data Fig. 8c,d), contrary to what is often observed during learning in animals.

Vanilla RNNs

We implemented custom RNN models to learn the structure of the 2ACDC task. Task sequences incorporated numerical symbols with unique meanings: ‘1’ denoted the grey region; ‘2’ and ‘3’ represented near and far cues, respectively; ‘4’ and ‘5’ indicated near and far reward cues, respectively; ‘6’ symbolized reward; and ‘0’ denoted teleportation. An example of a near trial followed the structure: 1,1,1,1,1,1,2,2,2,2,1,1,1,4,6,1,1,1,5,5,1,1,0, and a far trial followed the structure: 1,1,1,1,1,1,3,3,3,3,1,1,1,4,4,1,1,1,5,6,1,1,0. We converted these numerical symbols into one-hot encodings to represent these categories. The RNNs consisted of an input layer, a recurrent hidden layer and an output layer. Both input and output layers contained seven units, corresponding to the unique sensory cues in the task. The hidden layer size varied between 200 and 5,000 units, depending on the specific variant. We explored four activation functions for the hidden layer: exponential softmax, ReLU, polynomial softmax and sigmoid. The exponential and polynomial softmax functions implemented a soft winner-take-all mechanism, whereas ReLU and sigmoid provided more traditional activation patterns. The models were trained using backpropagation through time with the Adam optimizer. Learning rates ranged from 0.002 to 0.2, adjusted based on the activation function to ensure stable training. We used cross-entropy loss as the objective function. For each simulation, we generated sequences of 40–100 trials (random mixture of near and far trials), with half used for training and half for testing. Each trial consisted of 23 time steps corresponding to positions along the virtual track. Models were trained for 60–1,200 epochs. We ran multiple independent simulations with different random seeds to assess variability, ranging from 4 to 48 simulations depending on the specific model variant. To initialize the models, we used small random values drawn from a normal distribution for the weight matrices. The input-to-hidden and hidden-to-hidden weight matrices were initialized with a standard deviation of 0.001, whereas the hidden-to-output weight matrix used a standard deviation of 0.01–1, depending on the model variant.

Hebbian-RNN

Previous work³⁸ showed that a local Hebbian learning rule in a RNN can approximate an online version of HMM learning. We used an RNN consisting of K = 100 recurrently connected neurons and n = 96 feedforward input neurons. The feedforward input neurons carried orthogonal inputs for each of the 8 sensory stimuli, with 12 different neurons firing for each stimulus. The recurrent weights V and feedforward weights W were initialized from a normal distribution with 0 mean and standard deviation 2.5 and 3.5, respectively. The membrane potential of the kth neuron at time t is given by \(u_k^t=\sum _i^Nw_kix_i^t+\sum _j^Kv_kj\,y_j^(t-\Delta t)\), where w_ki is the feedforward weight from input neuron i to RNN neuron k, v_kj is the recurrent weight from neuron j to neuron k, Δt = 1 ms is the update time, and \(x_i^t\) and \(y_j^t-\Delta t\) are exponentially filtered spike trains of the feedforward and recurrent neurons, respectively (exponential kernel time constant of 20 ms). The probability of neuron k firing in Δt was computed by exponentiating the membrane potential and normalizing it through a global inhibition, \(f_k=\frace^u_k\sum _l^Ke^u_l\). For each neuron k, spikes were generated with a probability of f_k by a Poisson process, with a refractory period of 10 ms during which the neuron cannot spike again. When the postsynaptic neuron k spiked, then the weights onto neuron k were updated as \(\Delta w_ki(t)=\alpha (e^-w_kix_i(t)-0.1)\) and \(\Delta v_kj(t)=\alpha (e^-v_kjy_j(t)-0.1)\), where α is the learning rate (0.1) and \(y_j(t)\) is the exponentially filtered spike train. Both weights V and W were kept excitatory. We computed the correlation between the RNN representation of different positions in the near and far trial types at different stages during learning and compared it with the cross-correlation matrices for mice.

LSTM

We implemented LSTM networks using the same task structure and input sequences as the vanilla RNNs. The LSTM model consisted of a single LSTM layer with 500–1,200 hidden units, followed by a linear readout layer. Both input and output layers contained seven units, corresponding to the unique sensory cues in the task. The LSTM processed the input sequence and produced hidden states for each time step. These hidden states served as the primary output for analysis and were also passed through the linear readout layer to generate predictions. We explored several LSTM variants, including a standard model, one with L1 regularization on hidden states, another with dropout applied to the hidden states, and a version with a correlation penalty to encourage decorrelation between hidden states of different trial types. These models were trained using the Adam optimizer with learning rates between 3 × 10⁻⁴ and 5 × 10⁻⁴, using cross-entropy loss as objective function. Training proceeded for 200–300 epochs on sequences of 100 trials, with half used for training and half used for testing. We conducted multiple independent simulations with different random seeds. For all LSTM variants, we analysed the hidden state dynamics (cell states for some variants), examining their correlation structure between different trial types and the accuracy of the model in predicting reward locations.

Transformers

We implemented a transformer architecture based on the minGPT repository (https://github.com/karpathy/minGPT), specifically using the GPT-micro configuration. This model uses 4 layers, 4 attention heads and an embedding dimension of 256. The transformer was adapted to learn the 2ACDC task structure, using the same input encoding as the vanilla RNN and LSTM models. We generated sequences of trials with random starts, totalling 1,000–3,000 batches. Each batch consisted of ten randomly assembled trials. From these, we selected random 100-element chunks to form our input sequences. The vocabulary size was set to match our dataset, and the block size (maximum sequence length) was adjusted based on our experiments with different context lengths. To address the sequential nature of the task, we trained transformers with various context lengths ranging from 1 to 100, finding that lengths exceeding 4 were sufficient to solve the task. This threshold is specific to our task structure, allowing disambiguation between reward locations given the inter-reward grey cue length of 3. The transformer was trained using the Adam optimizer with a learning rate of 3 × 10⁻⁴ for 600–2,000 iterations. The objective was to predict the next sensory symbol, using cross-entropy loss. During testing, we primarily used four-symbol sequences to evaluate the next-input prediction accuracy of the model. For analysis, we examined the pre-logit layer of the transformer, as it represents the final stage of feature extraction before classification, potentially capturing the most task-relevant information. Our key findings regarding the representational structure were robust across different context lengths, up to 100 symbols.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.