Emergence of collective oscillations in massive human crowds

Image acquisition, density and velocity measurements in the Chupinazo crowd

In this section, we explain how we film the dense crowds and how we convert raw images into quantitative data.

The Chupinazo crowd

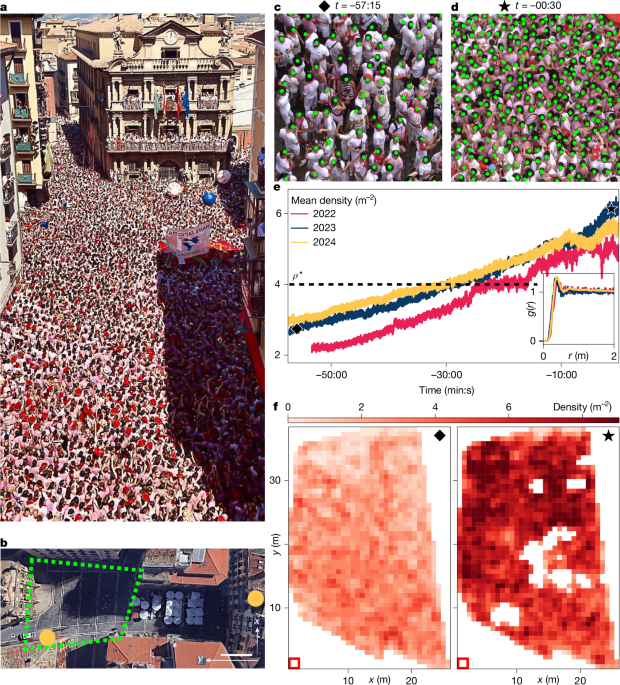
The crowds we film in Pamplona are composed of the attendees of the San Fermín festival. Most of them are locals who are well aware of how the event unfolds: they know the dress code and when to raise their red handkerchiefs, and they eagerly await the orchestra after the festival opening speech and fireworks. Many foreign tourists are also present, and the crowd consists mostly of young adults of all genders. As the Chupinazo is broadcast on the Spanish national networks and popularized internationally, we can assume that most of the participants are aware of the high crowd density that they will be confronted with before gathering. As a result, participants of the Chupinazo come in a festive mood, with evident signs of alcohol consumption. When the crowd is sparse, small groups of people can be seen singing, clapping and lightly pushing each other without creating significant movement. However, when the crowd density exceeds ρ*, we observe high-amplitude motions, referred to as crowd quakes in a different context²¹. Unlike, for instance, at heavy-metal concerts, there are no signs of individuals actively pushing others when the crowd is dense; instead, people try protecting themselves from the crowd. Lastly, those unable to enter the square at the entrances keep on accessing the Plaza Consistorial and pushing inwards. Two entrances are blocked by police forces until just a few minutes before noon. Here, hundreds of people (mostly locals) try gathering in the already crowded square. The number of people on the Plaza Consistorial peaks at noon and can be as large as about 6,000 people.

We filmed four Chupinazo events, in 2019, 2022, 2023 and 2024. The 2020 and 2021 editions were cancelled because of COVID-19 restrictions. The weather was sunny in 2019 and 2023. It was cloudy and rainy in 2022 and 2024. We were not informed of and did not observe any change in the organization of the ceremony.

Image acquisition

We recorded videos from the two observation spots indicated in Fig. 1b. In 2022, 2023 and 2024, we used Sony FDR-AX33 and Sony FDR-AX43A camcorders on both spots. The frame rate was 25 frames per second and the resolution was 3,840 × 2,160 pixels (4K videos). In 2019, we used telephoto lenses (Sigma 150–600 mm F5-6.3 DG OS HSM ∣ S) mounted on Nikon D500 cameras with a frame rate of 30 fps and a resolution of 3,840 × 2,160 pixels. We illustrate the observation set-up in Extended Data Fig. 6. The cameras were mounted on standard tripods on the balcony of the leftmost building (fifth floor of the tourism office of Pamplona, 2023 and 2024), and on custom mounts on the rightmost observation point (private balcony on the fourth floor of the highest building surrounding the Plaza Consistorial, 2019, 2022, 2023 and 2024).

Image correction protocol

We used the same protocol as in ref. ¹² to correct for the perspective distortions. In short, we mapped the pixel coordinates (u, v) of every frame to a coordinate in the square frame (x, y, z). The goal was to generate images with fixed pixel dimensions in metres. This was done using planar homography, assuming pinhole cameras and neglecting the height of the z axis³⁰. To do so, we first selected a reference image of the plaza (Extended Data Fig. 7a) when clear of pedestrians. We chose a set of four points distributed over the square and matched them on a satellite view from Google Earth Pro (Extended Data Fig. 7b). We then computed the planar homography matrix using these four points from the two views and rescaled all the images accordingly. Finally, by measuring the distances on the satellite view in metres and in pixels, we determined the size of the pixels in metres. In the rescaled images, all the pixels have the same dimensions (Extended Data Fig. 7c). In Extended Data Fig. 7, we show the set of points used in 2023, on the raw image, the satellite view and the resulting rescaled image. The pixels on the corrected images are almost squares and their dimensions respectively in the x, y directions correspond to 0.028 × 0.029 m, 0.046 × 0.045 m, 0.012 × 0.012 m and 0.013 × 0.012 m in 2019, 2022, 2023 and 2024, respectively.

To estimate the relative error caused by the planar homography protocol, we compared the distances between the original reference points with the distances measured in our corrected images. We found the following relative errors respectively in the x, y directions: 1% × 12%, 1% × 1%, 1% × 3% and 1% × 3% in 2019, 2022, 2023 and 2024, respectively.

As in ref. ¹², we also corrected for the zero-height approximation. Previously, we assumed that all visible pixels in the images lie on the same plane as the ground. However, we observed the heads of pedestrians that are not on the ground. Here we recall the formula and give the values measured for the zero-height approximation correction. More details can be found in ref. ¹². Let Δx′ represent the distance measured between two heads in images corrected for perspective distortion. Owing to the height of pedestrians, that distance is overestimated. Let Δx denote the distance between the feet of the same pedestrians in the same image. These distances are related by the following equation

where H is the height of the observation spot and h is the typical height of pedestrians. This relationship is valid in all direction and is independent of the position in the image. We set h = 1.73 m based on the average height of Spanish people and we estimated H = 16 ± 1 m by using a picture of the buildings with pedestrians serving as a length reference³¹.

Finally, in 2019, the weather was sunny and the shadow cast by the buildings introduced artefacts in our particle image velocimetry (PIV) measurements (Fig. 1a). To address this issue, we performed an additional image processing step. We used a Python script available on GitHub to homogenize the brightness of the image^32,33. This procedure removed all the PIV artefacts that arise at the edge of the building shadows.

Time interval of unguided crowds

Each year, we focus on an approximately 1-h time interval. We defined the origin of time as when the festival attendees raise their red handkerchief to signal the opening of the festival and change their behaviour according to the Chupinazo tradition. This happens around noon, and before the festival officially starts no external guidance dictates the dynamics of the crowd. No acoustic, visual or mechanical signal coordinates the motion of the crowd.

Spatial delimitation of our measurements

Before the opening of the festival, part of the celebration consists of holding large flags and playing with big balloons on the square (Extended Data Fig. 7d). When we measured the density and velocity fields, we needed to make sure to consider only the regions of space devoid of these objects that obstruct our field of view.

To do so, we used a standard machine learning tool, YOLOv8³⁴. It is designed to detect specified objects on images. We trained it on 15 images from 2019 and 2022 by manually annotating the polygons enclosing the balloons and flags on our pictures. In practice, we annotated the images using the labelstudio software on the raw images. The area and position of the detected objects were then corrected using the planar homography parameters and converted into dynamical masks applied to every frame (Extended Data Fig. 7e). Both the density and the velocity fields were computed on the masked images (Extended Data Fig. 7f).

Detection of the attendees and density measurement

To detect the position of the head of the people in the crowds, we took advantage of the machine learning algorithm P2PNet³⁵. It is designed to estimate the number of people in a picture based on a convolutional neural network pretrained on 300 images with dense crowds (ShanghaiTech dataset³⁶). We further trained the neural network on 4 manually annotated images taken from our 2019, 2022 and 2023 footage. To annotate the images, we used a homemade Python script and trained P2PNet for 3,500 epochs of 4 batches. The discrepancy between the automated and manual counting procedures in the full field of view of a picture is smaller than 5%. We detected the heads on the raw images (Fig. 1c,d).

We aimed to clean the data before computing the density by minimizing the impact of false positives and missed detections. Given that pedestrians continuously appear in the frames, they are more likely to be correctly detected compared with the occurrence of false positives or misses. We predicted that detection errors manifest as high-frequency ‘flashes’. To counteract this, we converted the detection data into a density field by applying a Gaussian convolution over the detected points where 3σ approximately equals the size of a head, σ being the typical width of the two-dimensional Gaussian. This density field was then averaged over 0.4 s, and a 33% threshold was applied to retain only points of high occurrence. A maxima-finding algorithm was subsequently employed to obtain the cleaned detection data.

To define the density field, we used the same windows (dimensions and locations) as the velocity field (Supplementary Table 1). In each window, approximately 1.5 × 1.5 m² in size, we counted the number of people and divided this value by the window area. Given the quality of our images, we were able to detect the individuals and define the local density field in the region shown in Fig. 1b only for our 2022, 2023 and 2024 images.

We used trackpy³⁷ to measure the trajectories shown in Fig. 3d.

Measurement of the velocity field

We describe Chupinazo crowds as continua. As frequently used in fluid mechanics, we measured the Eulerian velocity field in the crowd using conventional PIV¹². We used a typical window size of about 1.5 m and a typical time step of about 0.5 s. The precise different values to characterize the observed dynamics are summarized in Supplementary Table 1. The measurement error of the two components of the velocity field in a single PIV box is of 0.1 m s⁻¹ in 2019 and 2022, 0.05 m s⁻¹ in 2023 and 2024.

Image acquisition, density and velocity measurements in the 2010 Love Parade

In this section, we explain the origin of the data and the process of converting raw images into quantitative data.

The Love Parade 2010

The Love Parade 2010 was a music festival held in July in Duisburg, Germany⁴. During the event, 21 people died and more than 500 were injured at the main entry of the festival area (Extended Data Fig. 8). This traumatic event has been the subject of numerous scientific studies, also because a number of videos showing the convergence towards the catastrophe have been publicly released⁴.

Videos

Numerous recordings from mobile phones and cameras are available on the internet. The organizer released some camera footage of the main entry where the catastrophes occurred, before they happened (https://www.youtube.com/watch?v=QpzISdBE3dA). We selected two clips (clip 1 from 14:04 to 15:46 and clip 2 from 19:24 to 19:49) where we observed high-amplitude motion of the crowd.

Image correction protocol

We were unable to perform any image correction on the Love Parade 2010 data.

Density measurement

We were unable to measure the density in clip 1 owing to the low resolution, which hindered detection and manual annotation. In clip 2, we annotated one image. We estimated the area covered by the field of view by measuring the shoulder-to-shoulder width of festival attendees in pixels and then converting it to metres. Our estimate of the crowd density is ρ = 8 ± 1 m⁻².

Measurement of the velocity field

We used the same methodology for the Chupinazo and the Love Parade crowds. We measured the Eulerian velocity field in the crowd using conventional PIV¹². As not enough reference points are visible on the images to perform perspective correction, we used the raw images to measure the approximated velocity field. We summarize the values of the different parameters chosen to characterize the observed dynamics in Supplementary Table 1.

Power spectra

We use the same methodology as for the Chupinazo crowds.

Characterization tools

We developed all our numerical tools using mostly the numpy package of the Python numerical language.

Radial pair correlation function

We used data from the detection of the attendees (see above) and the function static.pair_correlation_2d from trackpy³⁷, which takes into account non-periodic boundary conditions. The radial pair correlation function is computed in a rectangle devoid of flags and balloons and averaged over a period of about 7 minutes in the densest crowds (see below).

Power spectra

To compute the power spectra of the velocity v(r, t), velocity orientation \(\hat{{\bf{v}}}({\bf{r}},t)\), and squared speed v²(r, t) fields of Fig. 3a–c, we first computed the discrete-time Fourier transform for each position r using the numpy.fft.fft function. For the sake of consistency, we normalized these values by the total duration of the signal. A perfect cosine signal with pulsation ω₀ would have a discrete-time Fourier transform showing peaks of amplitude 1/2 at ±ω₀. The local spectra are given by the squared norm of each discrete-time Fourier transform signal. Finally, we performed spatial averages of the local spectra to compute S_v(ω), \({S}_{\widehat{{\bf{v}}}}(\omega )\) and \({S}_{{v}^{2}}(\omega )\). These spectra were computed using signals of duration 6 min 30 s for the 2023 data, 7 min 30 s for the 2022 data and 30 s for the 2019 data. In 2019, the safety system of our cameras reset them approximately every 30 s owing to overheating. We therefore computed our spectra over shorter time intervals, but averaged them over all our 30-s-long acquisitions.

To accurately compare the 2019, 2022 and 2023 spectra, we divided the spectra by their mean value between ω = −2 rad s⁻¹ and ω = 2 rad s⁻¹ and the final spectra were obtained after a final smoothing over 5 subsequent data points.

Time–frequency characterization

To perform the time–frequency analysis of Fig. 3f, we applied the above method to compute the power spectra on time intervals [t, t + Δt] with Δt = 3 min and repeated the same operation for increasing values of t with a step of 1 s.

Correlation lengths

To compute the radial correlation functions of the velocity, orientation and speed fields, we first computed their two-dimensional spatial correlation functions. The value of the correlation C_f(R) of a vector function f(r, t) is given by

where δf(r, t) = f(r, t) − ⟨f(r, t)⟩_r,t and with ⟨⋅⟩_r,t standing for an average over positions r and time t. In practice, we compute the value of δf at the point r + R using numpy.roll to shift the data that form the vector δf(r). We then use numpy.nanmean to compute the averages. We parallelized this computation using multiprocessing.Pool. To compute the radial correlation function, we created bins corresponding to radial displacements. For a bin ranging from r₀ to r₀ + δr, we averaged all the values of the two-dimensional correlation function C(R) for r₀ ≤ ∣R∣ < r₀ + δr. We defined the instantaneous correlations by performing the time average over 3-min-long intervals. We defined the correlation lengths as the distances at which the radial correlation functions reach the value 0.1.

Chirality of the local dynamics

Here we focus on the oscillatory component of the crowd motion. We first applied a temporal band-pass filter to the velocity field. The filter width was set to the full-width at three-quarter maximum height of the power spectra shown in Fig. 3a. In practice, we performed a time Fourier transform on the velocity field, we applied the band-pass filter and performed an inverse Fourier transform.

We defined the local spin field ϵ(r, t) as the sign of the instantaneous increment of the angle θ made by the velocity with the x axis. For each position in space, we computed the orientation of the filtered velocity field \(\theta \,\in \,[{\rm{-\pi }},{\rm{\pi }}]\). We healed the discontinuities of θ(r, t) so that \(\theta \,\in \,[-\infty ,\infty ]\). We performed a moving average of time window T₀/2, with T₀ = 2π/ω₀ and ω₀ the pulsation of the maximum of the power spectrum. At each position r and time t, we measure the sign ϵ(r, t) of the time variations of θ(r, t), which defines the spin field ϵ(r, t) = ±1. We illustrate this protocol in Extended Data Fig. 9 and show the resulting spin fields for the 2022 event, which reveal the same phenomenology as in Fig. 4. We estimated the error bars of the spin field distribution using the jackknife method over 10,000 samples³⁸. For the correlation length of the spin field, we ran the band-pass filter on time windows of 3 min and computed the correlation length as detailed above.

Phenomenological inference of the active friction laws

In this section, we show that confinement and odd frictional forces conspire to yield spontaneous chiral oscillations at an incoherent speed in dense crowds.

Odd friction and spontaneous symmetry breaking

Our starting point is the mean-field description of the crowd mechanics, which takes the form of Newton’s second law ∂_tv = f/ρ, where ρ is the mass density and f is the sum of all the body forces originating from the interactions between the pedestrians and the ground or between the pedestrians and the confining walls. We decompose it into four terms: f(t) = −ργv(t) + ρp(t) − ρku + ρσζ(t), where the first drag term classically models the damping of the velocity fluctuations via the momentum exchange with the ground. In the spirit of a Landau expansion, we retain the lowest-order term in v and consider a linear drag force. The second term is what we refer to as an active friction with the ground. It is a vector that models the conversion of the body deformations into propulsive forces. The third term stems from the confinement of the crowd by walls. Again, in the spirit of a Landau expansion, we retain the lowest-order term in the displacement variable u (with v = ∂_tu). The last term in the force definition is a Langevin noise source that classically accounts for the coupling to all the fast degrees of freedom ignored within our mean-field picture. ζ(t) is a Gaussian random noise of zero mean and covariance \(\langle {\boldsymbol{\zeta }}(t){\boldsymbol{\zeta }}({t}^{{\prime} })\rangle =\delta (t-{t}^{{\prime} }){\mathbb{I}}\).

In Supplementary Information, we show that the constitutive relation that defines the propulsive force p cannot take the form p(t) = f(v(t), u(t)) (see also Extended Data Fig. 5a–c). In others words, we must take into account the proper dynamics of p. Because the crowd is globally isotropic (Extended Data Fig. 4) and has no reference position in space, the constitutive equation must be independent of u and invariant upon rotations. Furthermore, our experimental observations show that the parity symmetry of the crowd is not explicitly broken. We thus proceed to a systematic Landau expansion to find the most general constitutive equation. Restricting ourselves to first-order derivatives in time and keeping only the leading-order nonlinearities, corresponding to the six third-order terms, we find

where ηs are material parameters and ζ_p(t) is another Gaussian random noise of zero mean, covariance \(\langle {{\boldsymbol{\zeta }}}_{{\bf{p}}}(t){{\boldsymbol{\zeta }}}_{{\bf{p}}}({t}^{{\prime} })\rangle =\delta (t-{t}^{{\prime} }){\mathbb{I}}\) and uncorrelated from ζ(t). We discuss in Supplementary Information the effect of all terms and all nonlinearities in Newton’s second law and equation (6). We study them one at a time to single out their impact on the crowd dynamics. The conclusion of this thorough investigation is that our experimental findings are nicely captured by a minimal model where inertia plays a negligible role and where only two nonlinearities rule the dynamics of the p variable. The α² term which we refer to as a ‘weathercock’ term in the main text is essential to yield chiral orientational oscillation. However a second nonlinearity is required to stabilize the oscillatory dynamics against fluctuations. More accurately, we show that the dynamics is unstable when all the η_i vanish. However, stable chiral states can emerge when η₁ ≠ 0, η₃ ≠ 0 or η₅ ≠ 0. As the stability domain of the chiral states is much larger when stabilized by a nonlinear windsock effect (η₃ and η₅), we therefore focus on a minimal model where we disregard inertia and retain only the α² and η₃ nonlinearities.

The mechanics of dense crowds is then captured by a minimal set of two equations:

where we have set all η_i to zero, except η₃ ≡ η/γ_p. The first equation corresponds to Newton’s second law and the second equation is the constitutive equation of the crowds. We provide a physical interpretation of this constitutive relation in the main text. The nonlinear η term implies that the amplitude of the windsock effect decreases as the amplitude of the propulsive force increases. We also note that this equation is strikingly similar to the mechanical description of active solid metamaterials derived in ref. ²⁷ from a microscopic model. Only the sign in front of the double cross-product is different.

Although equation (7) has a clear physical meaning, it is unpractical to investigate the fixed points, the limit cycles and the stability of the dynamics. To characterise the deterministic dynamics of our nonlinear system (σ = σ_p = 0), we write \({\bf{u}}=v\widehat{{\bf{u}}}\), with u the norm of u and \(\widehat{{\bf{u}}}\) its orientation. We then inject this form into equation (7), and express the dynamics in terms of the three variables u (the displacement magnitude), v = ∂_tu (the ‘speed’) and \({\varOmega }^{2}={({\partial }_{t}\widehat{{\bf{u}}})}^{2}\) (the square of the angular velocity of \(\widehat{{\bf{u}}}\)). We then find

with β_c = γ + k/γ_p. We stress here that the dynamical variable Ω² does not prescribe the direction of rotation of u but only its rate of change.

Fixed points and limit cycles

We now look for the fixed points of the dynamics (u_⋆, v_⋆, \({\varOmega }_{\star }^{2}\)) by setting the partial derivatives to zero in equation (8). The first fixed point is trivial and corresponds to quiescent crowds where u_⋆ = 0 and v_⋆ = 0, whereas \({\varOmega }_{\star }^{2}\) is ill defined as the displacement vanishes (u_⋆ = 0). There also exists a second pair of non-trivial fixed points for β > β_c characterized by v_⋆ = 0

and

This second pair of fixed point corresponds to two circular limit cycles for u (and v). The radius of the limit cycles is u_⋆ for u (and u_⋆∣Ω_⋆∣ for v), and they are swept at opposite angular frequencies ±Ω_⋆. To make sure that these two limit cycles explain the oscillatory dynamics of our crowds, we must first show that they are stable to small perturbations.

Linear stability of the fixed points and limit cycles

We now study the linear stability of the two fixed points. For the trivial fixed point, we linearize equation (7) in the noiseless limit around (u_⋆ = 0, p_⋆ = 0), and find

The trace of the matrix is γ_p(β − β_c)/γ. It changes sign when β = β_c. The determinant is given by kγ_p/γ and always remains positive. We thus conclude that the trivial fixed point is stable if β < β_c, as the matrix has two eigenvalues with a negative real part. Instead, the matrix has two eigenvalues of positive real part when β > β_c and the quiescent fixed point hence becomes unstable. This criterion coincides with the emergence of the limit cycles.

We now address the stability of the two limit cycles. We set u = u_⋆ + δu, v = δv and \({\varOmega }^{2}={\varOmega }_{\star }^{2}+\delta {\varOmega }^{2}\) and linearize the above equations with respect to δu, δv and δΩ². We find

The eigenvalues μ of the Jacobian matrix are solutions of the cubic equation −μ³ + τμ² + νμ + Δ = 0, with τ the trace and Δ the determinant. The three coefficients of the characteristic polynomial depend on β and read

The limit cycles are stable if the three eigenvalues have a negative real part. This is equivalent to imposing that τ < 0, Δ < 0 and ν + Δ/τ < 0. In Supplementary Information, we analyse extensively the conditions under which these three inequalities are verified. We show that there are ranges of parameters for which the limit cycles are stable for all values of β, leading to stable chiral states above β_c. Instead, there are some other ranges of parameters for which the limit cycles can destabilize for some values of β. Our results are summarized in the stability diagram = (γγ_p/k, γη/α²) shown in Extended Data Fig. 10.

We have therefore shown that our mechanical model of confined dense crowds evolves according to a dynamics that cannot be captured by a steepest descent in an effective potential. This so-called non-reciprocal and nonlinear dynamics is here characterized by a mean-field phase transition (a bifurcation) from a trivial state to a chiral state where v chases p while p runs away from v along circular trajectories swept at constant rate. This stationary chiral dynamics can operate along two possible directions selected by initial conditions. The parity symmetry of the dynamics is spontaneously broken.

Crowds as frictional odd matter

Our stability analysis shows that the propulsive force must relax faster than the displacement field to observe spontaneous oscillations: γ_p > k/γ. This finding a posteriori justifies the relevance of the asymptotic analysis γ_p ≫ k/γ discussed in the main text, which we now detail (see also Supplementary Information). In this limit, we can ignore the time variations of the fast variable p, which is instantly slaved to u (in the absence of noise). We can then generically decompose p as p = (−K_∥ + k)u + K_⊥u^⊥, and solve for K_∥ and K_⊥ by using this form in the algebraic equation satisfied by p:

where we have used Newton’s second law to express v = ∂_tu, as a function of u and p. We are then left with a single equation for the degree of freedom u that takes the form ∂_tu = −∇V_eff(u) ± (K_⊥/γ)u^⊥, where ∇V_eff(u) = K_∥u. The dynamics of the crowd is akin to that of a particle falling in an effective potential V_eff and couples to a nonlinear odd spring K_⊥. Again the sign of K_⊥ is not a priori specified and can take both values with equal probability. We sketch the dynamics of the particle in Fig. 5e. Deep in the chiral phase (β ≫ β_c), V_eff has the shape of a ‘Mexican hat’. Once the particle reaches the minimum of the potential, u takes a finite value. In turn, the particle dynamics orbits at constant speed along the ground-state circle under the action of of the odd spring force either in the clockwise or anticlockwise direction depending of the sign of K_⊥. This minimal model nicely captures the chiral dynamics of the dense crowds and provides an intuitive explanation for its nonlinear dynamics.

Numerical methods

Numerical integration schemes

We solve equation (7) using a fourth order Runge–Kutta scheme³⁹, with a time step δt (see below). We compute the velocity, orientation and speed spectra for n_run different realizations of the random noise forces and random initial conditions. All spectra are measured in a steady-state regime after n_st preliminary integration steps specified below.

The definition of the spin ϵ(t) requires filtering the velocity field. To do so, we computed the mean velocity spectrum S_v over the n_run runs and performed a moving average of size n_w = 10. We then defined our band-pass filter by considering only the angular frequencies ω for which the value of the smoothed spectra satisfies \({\max }_{{\omega }^{{\prime} }}{S}_{{\bf{v}}}({\omega }^{{\prime} })-{S}_{{\bf{v}}}(\omega )\le [{\max }_{{\omega }^{{\prime} }}{S}_{{\bf{v}}}({\omega }^{{\prime} })-{S}_{{\bf{v}}}(0)]/4\) (quarter-difference between the maximum and the value of the spectrum at zero angular frequency). We finally used inverse fast Fourier transform to compute the filtered signals \({\widetilde{v}}_{x}\) and \({\widetilde{v}}_{y}\). From these filtered signals, we then determined the angle that the filtered velocity field makes with the x axis: \(\theta =\arctan ({\widetilde{v}}_{y}/{\widetilde{v}}_{x})\). The resulting discontinuous time series was defined on the unit circle. We then unwound this time series to define the orientation angle over \({\mathbb{R}}\). Finally, we defined the spin ϵ(t) as the sign of the difference between two consecutive values of the orientation angle.

We estimated the error bars associated with the power spectra and histograms of ϵ using the jackknife method over n_run measurements³⁸.

Simulation parameters

Without loss of generality, we can set γ = 1 and α = 1, which amounts to defining our units of length and time. The model has then six control parameters, which are β, γ_p, k, η, σ and σ_p. To integrate the equations of motion, we set δt = 0.001, so that the damping coefficients in equations (1) and (2) verify k/γ ≳ 20δt and 1/γ_p ≳ 100δt for the typical values of γ_p and k that we consider. This value of δt also ensures that the angular frequency Ω_⋆ always remains in our simulation window. The number of steps n is set so that the system explores exhaustively its phase space. Finally, the number of steps n_st = 1.5 × 10⁵ is set so that the system reaches the limit cycle when β > β_c.

The n_run = 100 simulations are initialized on one of the limit cycles in the absence of noise when β > β_c, namely, \({\bf{u}}={u}_{\star }(\cos \varphi \,\widehat{{\bf{x}}}\,+\) \(\sin \varphi \,\widehat{{\bf{y}}})\) with φ drawn uniformly in the range \([{\rm{-\pi }},{\rm{\pi }}]\), and \({\bf{p}}={u}_{\star }\sqrt{{k}^{2}+{\gamma }^{2}{\varOmega }_{\star }^{2}}[\cos (\varphi +{\phi }_{\star })\,\widehat{{\bf{x}}}\,+\) \(\sin (\varphi +{\phi }_{\star })\,\widehat{{\bf{y}}}]\), where \(\tan {\phi }_{\star }=\gamma {\varOmega }_{\star }/k\) with equal probability for the sign of Ω_⋆. Otherwise, the simulations are initialized from u = 0 and p = 0.

For Fig. 3a–c, we used k = 0.027, γ = 1.00, γ_p = 18.00, β/β_c = 1.10, η = 0.45, σ = 0.00 and σ_p = 2.00. For Fig. 3f, we used γ = 1.00, γ_p = 18.00, η = 0.45, σ = 2.00 and σ_p = 2.00.