Scaling and networking a modular photonic quantum computer

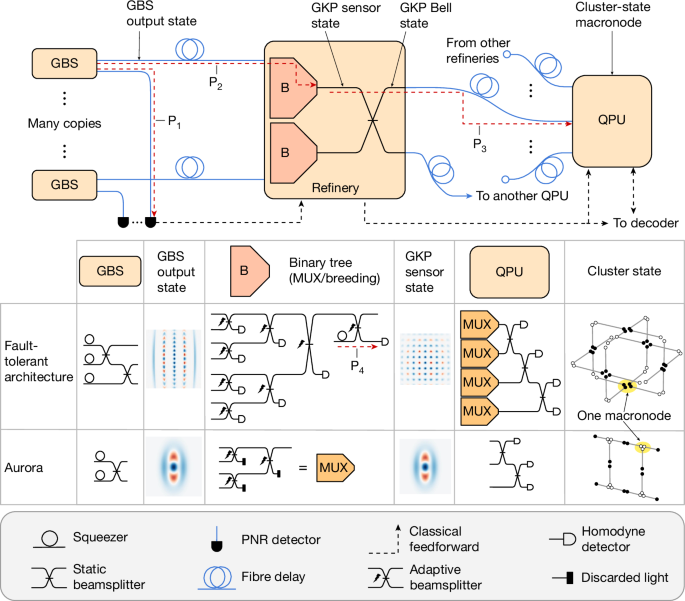
The Aurora hardware system (Extended Data Fig. 1) is composed of six distinct principal subsystems: (1) a customized master laser system provides coherent pump and local oscillator beams, as well as reference beams for phase stabilization; (2) a sources array generates squeezed light and two-mode Gaussian states; (3) a PNR detection system is used for heralding non-Gaussian states; (4) an array of refineries, each multiplexing eight inputs to one entangled pair; (5) a QPU array forms the spatial and temporal connections in the cluster state and performs homodyne measurements on each qubit; and (6) an array of fibre buffers provides appropriate phase- and polarization-stabilized delay lines between the sources and refineries, as well as between the refineries and QPUs. The entire system, apart from the cryogenic detection array, fits into 4 standard 19-inch server racks. Here we summarize the main features of these subsystems, as well as our method for verifying the multimode entanglement present in our cluster-state benchmark experiment; a more detailed exposition of these topics is available in Supplementary Information.

Laser system

The laser system is responsible for providing appropriate pump pulses (P1 and P2) to each squeezer in the sources array, a local oscillator beam temporally mode-matched to the quantum pulses for homodyne detection, and a variety of reference beams used to stabilize fibre delays (ref) and resonator positions (probe) throughout the rest of the system.

The laser system (depicted in Supplementary Fig. 24) begins with five narrow-linewidth lasers (P1, P2, local oscillator, ref and probe), all manufactured by OEWaves (OE4040-XLN) except for the probe, which was made by PurePhotonics (PPCL550). A broadband electro-optic frequency comb is derived from the local oscillator laser and serves as a frequency/phase reference to stabilize the remaining four lasers. Each laser is then modulated at the experimental clock rate of 1 MHz to provide temporal modes suitable to their purposes: the pump lasers are carved into 1-ns pulses (Exail MXER-LN-20, DR-VE-10-MO), the ref and probe lasers are carved into 400 ns (with AO Fiber pigtailed Pulse Picker from AA Opto-Electronic) and 50-ns pulses (using Exail MXER-LN-20), respectively, interleaved with the pump pulses at a later stage. The local oscillator laser has its complex temporal envelope mode-matched (using Exail MXIQER-LN-30) to the output of a representative squeezer (selection process is described in Supplementary Information). Each pulse train is amplified to a suitable power using erbium-doped fibre amplifiers (Model Pritel MC-PM-LNFA-20) before being combined into a polarization-maintaining fibre (with Opneti PMDWDM-1-1-CXX-900-5-0.3-FA). P1, P2 and local oscillator beams again have their phases stabilized, before being distributed among two sets of channels. The first channel, of which there are 24 copies, contains P1, P2, probe and ref, and is sent onwards to the sources array. The second channel, of which there are five copies, contains the local oscillator and ref, and is sent onwards to the QPU for coherent detection. Owing to the manner in which the beams are distributed, the ref laser carries the phase information in the system and thus can be used to stabilize measurement angles in the QPU. A second copy of the ref beam, slightly detuned in frequency, is sent on to the refinery array and used to stabilize interconnections between sources and refinery as well as between refinery and QPU.

Sources array

Each of the 24 sources chips are identical in design, and are based on the silicon-nitride waveguide platform provided by Ligentec SA and fabricated on their 200-mm production manufacturing line at X-Fab Silicon Foundries SE. Squeezers in these devices are based on a photonic molecule design, in which a pair of microring resonators are tuned to enable degenerate squeezed light to be generated using a dual-pump scheme, while leading-order unwanted parasitic nonlinear processes are suppressed⁶. The generated squeezed states are characterized using optical heterodyne tomography and found to be nearly single mode. The local oscillator temporal mode is matched to the dominant temporal mode as described in Supplementary Information. The outputs of the squeezers are passed through integrated asymmetric Mach–Zehnder interferometer (MZI) filters to remove pump light, then entangled by a tunable linear optical interferometer. Tuning of the interferometer, filters and resonators is accomplished using thermo-optic phase shifters. The chips are 8 mm × 5 mm in size, and are fully packaged and encased in a modular enclosure that mounts on a custom backplane chassis assembly. The end-to-end insertion loss (from pump input to quantum output) of the chips is 2.16 dB, and 1.82 dB of loss is experienced by the quantum light from when it is generated to when it is available in the fibre outputs. This figure includes an estimated squeezer resonator escape efficiency of (88 ± 3)%, filter and interferometer propagation loss of (0.36 ± 0.04) dB, and chip out-coupling loss of (0.90 ± 0.15) dB (81% coupling efficiency).

Newer designs based on different fabrication platforms and components, although not yet deployed in Aurora, have since been developed that combine multiple layers of thin silicon-nitride waveguides with a dispersion-optimized thicker layer, enabling much lower chip–fibre coupling loss, and higher squeezing through better suppression of parasitic nonlinear processes. Single-mode waveguide propagation losses of approximately 2.2 dB m⁻¹ have been demonstrated, with even lower losses available in wider cross-sections for resonators. Escape efficiencies in squeezer microresonator structures exceeding 98% are routine, but further improvements in design and fabrication are needed to maintain an acceptable loaded quality factor under such strong over-coupling conditions. Similarly, chip–fibre coupling from these devices with losses of approximately 0.1 dB have been observed, with simulations for future structures indicating that arbitrarily low losses are possible. These results are consistent with recent progress reports in low-loss quantum photonic component development²⁶. Even once realized, maintaining such low chip–fibre coupling losses through the packaging process in a manufacturing line capable of producing the millions of chips needed to furnish machines of practical utility remains an outstanding challenge.

PNR detection system

The PNR detection system is based on an array of 36 transition edge sensors (TES), housed in a pair of Bluefors (LD400) dilution refrigerators at 12-mK base temperature. These sensors are inductively coupled to an array of coherent superconducting quantum interference devices (SQUID) for cryogenic amplification, the signals from which are digitized and analysed in real time by an array of field-programmable gate array boards that discriminate photon number from the analogue pulses emerging from each sensor. Previously, such TES detectors were limited to repetition rates of a few hundred kilohertz, owing to their intrinsic thermal reset behaviour; higher experimental repetition rates required the use of demultiplexers²², which are undesirable owing to their added loss and complexity. The TES detectors employed in Aurora enjoy native operation at 1-MHz repetition rate, while preserving photon miscategorization error below 10⁻² for photon numbers up to 7. To enable this, the sensors were fabricated with small gold fins deposited at the margins of the tungsten absorber area; this engineers the thermal response of the detectors to absorbed photons to become faster by increasing the electron–phonon coupling with minimal impact on the other performance metrics of the detectors. The detection efficiency of this generation of TES detectors was not optimized for Aurora, and ranged from 97% to 69.3%.

The majority of the spread in this detection efficiency is believed to originate from variations in the detector packaging process. In Aurora, the deployed sensors were assembled by hand with no special quality assurance process enforced. More recently, TES detectors with operational speed at or above 1 MHz have been measured with consistently high detection efficiency above 90%. This is expected to increase to at least 97%, matching the best channels available in Aurora, as a more reliable packaging and assembly process is developed. Still, PNR detection efficiencies over 99% are needed to stay within the loss budgets for the P₁ path in our architecture (Fig. 1). Our simulations indicate that the primary challenge to achieving this, apart from repeatable and reliable assembly processes, lies in obtaining tight process control over the multilayer dielectric stack parameters used to form the optical cavity that enhances photon absorption in the tungsten film.

Refinery array

The refinery array consists of 6 nominally identical PICs, 14.6 mm × 4.5 mm in size, based on the thin-film lithium-niobate PIC platform offered by HyperLight and fabricated on a semiconductor volume manufacturing line. Two binary trees—each composed of three electro-optic Mach–Zehnder modulator switches—select, based on feedforward instructions provided by the PNR detection system, the switch pattern that optimizes the output state. These MZI switches have an average insertion loss of 0.19 dB, giving an average total insertion loss of 4.15 dB for the full optical path through each refinery chip, which includes the binary tree, chip in- and out-coupling, and Bell pair entangling beamsplitter losses. Pairs of refinery chips, all of which are fully packaged, are hosted in three rack-mounted enclosures. Appropriate duty cycling of the switch settings between quantum pulse time windows allows the voltage bias of each modulator to be continually monitored and locked, yielding an average switch extinction ratio of more than 30 dB.

In Aurora, the refinery chips implement probability-boosting multiplexing as well as Bell pair synthesis, but do not have homodyne detectors at the multiplexer switch outputs and thus do not implement breeding. Efforts are underway to integrate photodiodes into the refinery chip platform, and we expect the next generation of refineries to implement the full adaptive breeding protocol.

Although the modulation and detection bandwidths demanded by the refinery’s functions are not especially challenging compared with other applications, the loss requirements are. The importance of lower losses in MZI switches is compounded by the number of them present in the various optical paths. In the versions of the architecture contemplated in Fig. 4, the deepest combined path (P₂ and P₃ in Fig. 1) incorporates as many as 15 MZI switches. Even neglecting all other losses, this would mean that no more than approximately 7 mdB can be tolerated in each switch. Efforts to obtain this are well underway, with recent design and process optimizations yielding performance consistent with losses of 30 mdB per MZI switch. Early indications point to the importance of optimizing the thin-film lithium niobate (TFLN) etching process to manage scattering losses in the underlying waveguides. In addition, electrical control approaches must be engineered that enable high driving voltages. The MZI switch loss is nearly proportional to its length; shorter modulator sections are perfectly acceptable optically, but require proportionately higher applied voltages to operate. The driving approach must be scalable to allow operation of thousands of adaptive switches on the same chip. High-voltage-compatible integrated circuit fabrication nodes are being explored for this purpose. Other approaches using alternative materials such as barium titanate²⁶ have shown promise for delivering lower-voltage operation in this context, but further process improvements would be needed to compete with TFLN on raw propagation loss.

QPU array

The QPU array consists of 5 nominally identical modules, each based on a 300-mm silicon photonic-chip platform offered by AIM Photonics that hosts silicon-nitride and silicon waveguides, germanium photodiodes, and carrier depletion modulators. Within the chips, each measuring 6.2 mm × 4.3 mm and fully packaged within a rack-mounted enclosure, silicon nitride is used for edge coupling from the fibre inputs and for the interferometer that implements spatial entanglement in the cluster state. The quantum light then transitions to silicon waveguides and is mixed with local oscillator light on appropriate beamsplitters, and terminates on germanium photodiodes for homodyne detection. The loss experienced by each quantum input to the QPU is on average 3.68 dB, of which 0.82 dB arises from the edge couplers and optical packaging, 2 dB from the interferometer circuit and 0.86 dB from the photodiodes. The local oscillator input to one homodyne detector is modulated using silicon carrier injection modulators, with each quadrature phase setting actuated based on real-time instructions from the digital QPU controller. This controller is based on a field-programmable gate array, which is programmed to select the appropriate measurement bases, taking into account the algorithm and decoder protocol selected by the user.

The full signal chain latency from an optical pulse arriving at the homodyne detectors to the actuation of an updated local oscillator phase is approximately 976 ns. Out of this, 240 ns is spent on converting the optical homodyne pulse to a normalized 16-bit fixed-point number, involving photodiode response, transimpedance amplification, analogue-to-digital conversion, and digital signal processing for pulse integration and normalization. Another 672 ns is the worst-case serial link latency spent on serialization, propagation to the QPU backend, de-serialization of the 16-bit number, plus serialization, propagation back to each of the 5 QPUs, and de-serialization of the 2-bit local oscillator phase selection command. The remaining 64 ns are used for the decoder algorithm to calculate the next local oscillator phase setting from measurement information of all homodyne detectors from previous clock cycles. Future decoders requiring more digital clock cycles to carry out intervening computations could be deployed on digital circuits with higher clock speeds, or the increased latency could be offset by latency improvements in other parts of the signal chain. For example, latency could be improved by selecting lower-latency analogue-to-digital converters for digitizing the homodyne measurements, by optimizing the signal processing chain for homodyne value normalization, and by improving the serialization and de-serialization latencies associated with the serial links by means of using field-programmable gate arrays with high-speed (>1 Gbps) serial input/output pins for the QPUs.

The full fault-tolerant design, involving refineries that incorporate breeding, would have identical chip platform requirements for the refinery as for the QPU, those being electro-optic modulators and photodiodes. In the future, we thus expect both the refinery and the QPU to be based on the same PIC platform, which will look closer to the TFLN-based substrate used for the refinery in this work.

Our recent work optimizing the design of integrated photodiodes has yielded quantum efficiencies as high as 98.5% in the same germanium platform as that used in Aurora; the heterogeneous integration of high-quantum-efficiency photodiodes like these into TFLN devices is the last platform integration step required to equip Aurora with refineries capable of implementing breeding protocols. Considering this co-integration requirement with TFLN, our focus has turned towards using III–V-semiconductor-based photodiodes in place of germanium. Simulations indicate that evanescent coupling between TFLN waveguides and InGaAs photodiodes, appropriately fabricated, can deliver homodyne detectors with net quantum efficiency well above 99%. The most challenging aspect of achieving this lies in the details of the heterogeneous integration scheme used. High-quality surface preparations within deep trenches will be needed at the interface between the photodiodes and the waveguide cladding. Managing excessive dark current in the photodiodes themselves as their dimensions grow to accommodate near-unity absorption will also require innovative approaches.

Interconnects

Between the sources and refinery modules, and between the refinery and QPU modules, interconnects are required that can provide a specified and fixed delay on the quantum pulses conveyed. For the sources-to-refinery links, the delay serves as a buffer for awaiting heralding information from the PNR detectors, whereas the refinery-to-QPU links implement a delay of exactly one clock period on half of two different Bell pairs, enabling temporal entanglement in the cluster. The purposes of these delays differ slightly but they are otherwise identical in requirements. In particular, both must actively stabilize the link against fluctuating phase and polarization. This is accomplished by interleaving coherent classical reference pulses between each quantum pulse, interfering reference pulses between appropriate inputs to each chip, and feeding back on phase and polarization actuators in the fibre delay modules.

The delay lines themselves are implemented in discrete enclosed modules within the racks, and are each composed of a fibre coil of (253.286 ± 0.009) m (about 1.239 μs). It is noted that the fibre coils in 10 out of the 12 channels between refinery and QPU are (48.762 ± 0.004) m long (about 0.239 μs) such that the difference between the two interfering channel is exactly 1 μs. Each fibre coil is in thermal contact with a thermo-electric cooler, which provides slow phase tuning with a large capture range, compensating for phase drifts that arise from the unstable global temperature environment in the racks. These are accompanied by piezoelectric fibre phase shifters (Luna FPS-001) that provide fast phase control over a smaller range, locking against acoustic fluctuations. An electrical polarization controller (Luna MPC-3X) within each fibre module is used to ensure the inputs to each chip are aligned to the appropriate waveguide mode.

These custom first-generation modules were manufactured by Luna Innovations, and have an average loss of (0.28 ± 0.08) dB, excluding connectors, while adding between 0.6° and 1.5° of phase noise (root mean square), when in closed loop operation.

Recent prototype designs have demonstrated losses of <0.1 dB, of which 0.037 dB arises simply from the length of fibre itself in the delay. Future generations of this module are expected to be limited by only the fundamental propagation loss in the underlying fibre, which can be as low as 0.14 dB km⁻¹ in existing, commercially available products. Our initial studies have shown that the vast majority of the loss present in typical fibre delays arise from fibre connectors or splices between different constituent components. These are straightforward to eliminate by manufacturing fibre delay modules from a single draw of fibre. Thus, even without increasing the quantum clock speed beyond 1 MHz, using ultralow loss fibre and implementing these manufacturing changes is expected to achieve about 0.03 dB (0.7% loss). Going beyond this would require faster clock speeds or lower loss fibre. In addition, the inherent modularity of the architecture allows for all the fibre interconnections to be spliced, or indeed discrete fibre components in a given off-chip path to be assembled from a single draw of fibre.

Entanglement verification

To verify the generation of multimode entanglement, we investigate the nullifier variance⁴⁸ of the six Bell pair input states when the refineries are set to deterministically output squeezed states (that is, each pair is an approximate two-mode squeezed state). As we are interested in both q and p correlations, we alternate the cluster-state acquisition between the two measurement bases, measuring all modes in q and p, subsequently. Experimentally, the measurement basis was changed by a simultaneous phase rotation of all input modes using a setpoint change at our arbitrary-phase locks. For each basis, the data are acquired continuously over 2 hours, amounting to an uninterrupted measurement of 7.2 billion time bins (yielding 86.4 billion modes in total, combining all 12 operating modes at each time step). For the statistical analysis described below, the acquired data are processed in batches of 10 million time bins.

In the analysis, we obtain the statistical moments of the individual Bell pair states by ‘reverting’ the cluster-state stitch at the QPU (also known as synthesis of the macronode⁷). As a first step, we build the quadrature covariance matrix Γ of all measurement outcomes. The elements of the covariance matrix are given by Γ_ij = E(x_ix_j) − E(x_i)E(x_j), where a subscript represents a spatiotemporal mode and the operator E denotes the expected value (mean) of its argument. Our covariance matrix is of dimension 24 × 24 as we aim to capture not only the correlations among the 12 spatial modes but also their correlations to the quadratures of the subsequent time bin (12 modes for time bin t plus 12 modes for time bin t + 1). For this demonstration, we either measure all modes in \(\widehat{q}\) or all modes in \(\widehat{p}\), so we can build only the position–position or momentum–momentum subblocks of the full covariance matrix, which is sufficient for evaluation of Einstein–Podolsky–Rosen (EPR)-state nullifiers.

As part of the macronode synthesis, the six input Bell pair states are stitched together by a beamsplitter network, represented by the symplectic transformation S. In our second analysis step, we apply the inverse of that symplectic to our quadrature covariance matrix to obtain the covariance matrix before the macronode stitch: Γ_in = S^TΓS. This back-transformed covariance matrix now represents six separable EPR states. Their nullifiers are defined as \({\widehat{n}}_{q}=({\widehat{q}}_{0}-{\widehat{q}}_{1})/\sqrt{2}\) and \({\widehat{n}}_{p}=({\widehat{p}}_{0}+{\widehat{p}}_{1})/\sqrt{2}\). The variance of these nullifiers is obtained using the definition V(x_i ± x_j) = V(x_i) + V(x_j) ± 2cov(x_i, x_j), where all variance and covariance terms are obtained from the elements of Γ_in. To obtain the shot-noise reference for our EPR nullifiers, we apply the same operation to the vacuum data, obtained with all squeezed-light sources turned off.

It is noted that our method to evaluate the EPR nullifiers by applying the inverse macronode symplectic S^T to the output covariance matrix Γ is mathematically equivalent to applying S to the nullifier equations \({\widehat{n}}_{q}\) and \({\widehat{n}}_{p}\) and evaluating the resulting equations using Γ directly.

Adaptivity demonstration

In the adaptivity demonstration, we created the set-up for a distance-2 repetition code implemented through a cluster state composed of low-quality GKP states and squeezed states. Although the system is too noisy to show error suppression, we nevertheless demonstrate all the building blocks, collecting and processing of measurement data, running a decoder in real time, and performing a conditional operation at the following time step based on the recovery. The demonstration can be broken down into the following steps (Extended Data Fig. 2), with additional detail supplied in Supplementary Information section VII D:

1. 1.

   Initialization. In time step τ, homodyne measurements decouple qubits M₀, M₁, and M₂ (\(\widehat{q}\) measurements on all modes) and teleport qubits M₃, and M₄ (\(\widehat{p}\) measurements on modes 3 and 10, and \(\widehat{q}\) elsewhere) to initialize the experiment.

2. 2.

   Memory measurement. In time steps 2τ to 4τ, homodyne measurements are performed corresponding to two foliated repetition code checks (qubits M₀, M₃, and M₄ measured in X, that is, \(\widehat{p}\) measurements on modes 3 and 7, and \(\widehat{q}\) measurements elsewhere) and accompanying teleportations (qubits M₁ and M₂ measured in X, that is, \(\widehat{p}\) measurements on modes 4, 9 and \(\widehat{q}\) measurements elsewhere).

3. 3.

   Decoding. All decoding occurs in time step 4τ, as follows:

   1. (i)

      Inner decoding. The raw homodyne measurement outcomes from the previous steps, along with the state record (from photon-counting outcomes), are processed to obtain bit values and the probability of qubit error.

   2. (ii)

      Outer decoding. The syndrome and qubit error probability are passed to a qubit-level decoder. After a few iterations of the decoding algorithm (belief propagation), the decoder outputs the recovery along with updated estimates of error probabilities.

   3. (iii)

      Decision. A thresholding function is computed on the decoding output to assess confidence in the recovery. For a pre-determined threshold, we decide whether to ‘keep’ the entanglement and perform an additional repetition code check or to ‘cut’ the entanglement and restart the experiment. Steps i–iii constitute a complete real-time decoding round. In the control experiment (without feedforward), the decision bit (0 for ‘cut’ and 1 for ‘keep’) is added to a random bit, decoupling the decoding from the feedforward action.

4. 4.

   Feedforward and adaptive measurement. The decision based on the recovery obtained in time step 4τ is transmitted to qubit M₀ in the next clock cycle, at time step 5τ. The local oscillator phase of mode 7 in this qubit is changed accordingly. In the ‘keep’ case, this qubit is measured in X (mode 7 in \(\widehat{p}\)), preserving the entanglement, and in the ‘cut’ case it’s measured in Z (mode 7 in \(\widehat{q}\)), cutting the entanglement. Mode 6 is always measured in \(\widehat{q}\). Qubits M₁ and M₂ are measured in Z (all modes in \(\widehat{q}\)).

5. 5.

   Reset. Finally, also at time step 5τ, qubits M₃ and M₄ are decoupled through Z measurements (all modes measured in \(\widehat{q}\)) to reinitialize the experiment.

To confirm that the correct measurement has been performed, we plot correlations between four modes in the same clock cycle. In the ‘cut’ case, ideally no correlations should be observed, whereas in the ‘keep’ case, we expect to see cross-correlations between modes.

Data for the decoding demonstration are acquired in 69 batches of 1 million time bins each, amounting to a total of 69 million time bins and 13.8 million repetitions of the decoding algorithm. In the post analysis, the quadratures acquired in the final decoder time bin are separated into two groups, one for each of the two decoder-determined outcomes X and Z. Instances in which one or more cat inputs are involved in pairs 3 and 4 are discarded from the analysis. For both groups, we build a 12 × 12 covariance matrix of the quadratures acquired in the adaptive time step (corresponding to the central M₀ macronode and its neighbours). Classical cross-correlations among quadratures are obtained in a separate vacuum measurement (with squeezed-light sources disabled) and their covariance matrix is subtracted from the X and Z covariance matrices. Experimental covariance results are compared with theoretical predictions obtained from circuit simulations assuming that all modes were squeezed states with 4 dB of initial squeezing and 5% total efficiency (including optical loss and mode matching).

Optimizing candidate state factories for loss tolerance

We optimize over configurations of elements that produce GKP Bell pairs to be entangled into a cluster state. For the choice of cluster state, we select the Raussendorf–Harrington–Goyal cluster-state lattice^49,50,51. We use a two-layer decoder that first obtains a syndrome compatible with the ideal GKP qubit subspace, followed by a minimum-weight perfect matching algorithm⁵² to find a recovery operation that minimizes the probability of a logical error. The first ‘inner’ layer of this decoder scheme takes into account the correlations present in the noise arising both from the probabilistic nature of the state-generation process and from the extra modes present within each macronode and its neighbours (see ref. ³⁷ for more details). The second ‘outer decoder’ is also informed by a set of marginalized probabilities of errors furnished by the inner one. This strategy yields an effective squeezing threshold for fault tolerance of 9.75 dB, which improves on the 10.1-dB value found in ref. ²⁹. The quantum error correction (QEC) squeezing threshold defines the quality of the GKP states that must be available, which then determines the loss requirements for each path. The bound of the loss requirements for these paths can be found by searching different architecture configurations with loss included along each optical path. Full details of the calculations behind the effective squeezing metric and corresponding fault-tolerance thresholds are available in Supplementary Information.

The GKP-state factories considered in this work are parameterized by the GBS device settings (number of modes, levels of squeezing, interferometer angles, maximum detectable number of photons, loss levels), the refinery settings (depth of the binary tree, ranking function/selection rule of the refinery inputs, the number of refinery inputs to undergo breeding, degree of measurement-based squeezing, loss), and the QPU switch tree depth and associated loss. To evaluate a candidate state factory, we perform a Monte Carlo simulation to sample the distribution of output states over the PNR statistics of the GBS devices and the homodyne statistics of the refinery. From the distribution of states, we can determine the quality (symmetric effective squeezing) of the average Bell pair, taking into account the loss it will experience. (It is noted that that the symmetric effective squeezing of the refinery outputs is distinct from the amount of squeezing assumed in the GBS cells, which we fix to be 15 dB.) We leave P₁, P₂, and P₃ as free parameters but fix the P₄ path to be 40−50% of P₂ depending on the refinery depth as those paths have similar elements (the squeezers, chip input/output, fibres, homodyne detectors) and differ only by the binary tree of adaptive beamsplitters used for MUX and breeding. For more details, see Supplementary Information. The quality of the average state can then be compared with the 9.75-dB result of threshold calculations for the choice of cluster state and decoder to determine whether such states would be suitable for fault tolerance. Despite the states being highly non-Gaussian mixed states, we can simulate thousands of output-state samples from a single factory in a few minutes on a single core, and explore tens of thousands of factory candidates in reasonable time using a computing cluster. To achieve this, we employ different quantum optical representations at different stages of the state factory, namely, the Fock, Bargmann, characteristic and quadrature basis pictures, depending on what needs to be computed at that point in the factory (PNR statistics, GKP stabilizer expectation values, beamsplitter interactions, homodyne statistics). This is numerically implemented using MrMustard⁵³, an open source software package for simulating and optimizing quantum optics circuits.