User guide
When to use TabPFN
TabPFN excels in handling small- to medium-sized datasets with up to 10,000 samples and 500 features (Fig. 4 and Extended Data Table 1). For larger datasets and highly non-smooth regression datasets, approaches such as CatBoost9, XGB7 or AutoGluon40 are likely to outperform TabPFN.
Although TabPFN provides a powerful drop-in replacement for traditional tabular data models such as CatBoost, similar to these models, it is intended to be only one component in the toolkit of a data scientist. Achieving top performance on real-world problems often requires domain expertise and the ingenuity of data scientists. As for other modelling approaches, data scientists should continue to apply their skills and insights in feature engineering, data cleaning and problem framing to get the most out of TabPFN. We hope that the training speed of TabPFN will facilitate faster iterations in the data science workflow.
Limitations of TabPFN
The limitations of TabPFN are as follows: (1) the inference speed of TabPFN may be slower than highly optimized approaches such as CatBoost; (2) the memory usage of TabPFN scales linearly with dataset size, which can be prohibitive for very large datasets; and (3) our evaluation focused on datasets with up to 10,000 samples and 500 features; scalability to larger datasets requires further study.
Computational and time requirements
TabPFN is computationally efficient and can run on consumer hardware for most datasets. However, training on a new dataset is recommended to run on a (consumer) GPU as this speeds it up by one to three orders of magnitude. Although TabPFN is very fast to train, it is not optimized for real-time inference tasks. For a dataset with 10,000 rows and 10 columns, our model requires 0.2 s (0.6 s without GPU) to perform a prediction for one sample, whereas CatBoost (default) can do the same in 0.0002 s. In ref. 55, further optimizing TabPFN specifically for inference tasks has already been explored, resulting in four times faster inference performance compared with even XGBoost, but so far also reducing predictive quality. Refer to the section ‘Details on the neural architecture’ for details on the memory usage and runtime complexity of TabPFN.
Data preparation
TabPFN can handle raw data with minimal pre-processing. If we simply provide the data in a tabular format (NumPy matrix), TabPFN will automatically handle missing values, encode categorical variables and normalize features. Although TabPFN works well out of the box, we can further improve the performance using dataset-specific pre-processing. This can also be partly done automatically with our PHE technique or manually by modifying the default settings. When manually pre-processing data, we should keep in mind that the neural network of TabPFN expects roughly normally distributed features and targets after all pre-processing steps. If we, for example, know that a feature follows a log distribution, it might help to exponentiate it before feeding it to TabPFN. As TabPFN does z-normalization of all inputs, scaling does not affect the predictions. As for all algorithms, however, using domain knowledge to combine or remove features can increase performance.
Hyperparameter tuning
TabPFN provides strong performance out of the box without extensive hyperparameter tuning (see section ‘Comparison with state-of-the-art baselines’). If we have additional computational resources, we can further optimize the performance of TabPFN using hyperparameter optimization (HPO) or the PHE technique described in the section ‘TabPFN (PHE)’. Our implementation directly provides HPO with random search and PHE.
Details on the neural architecture
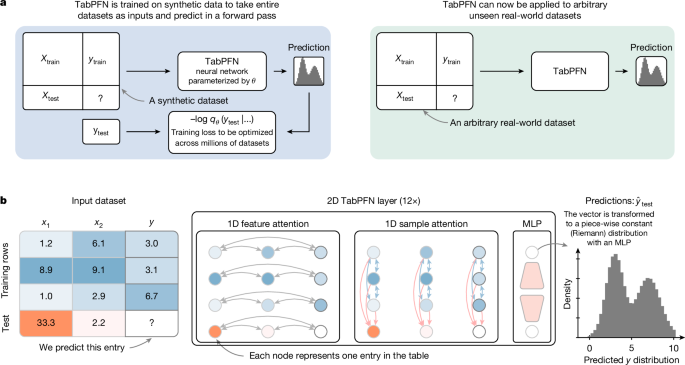
Our architecture is a variation of the original transformer encoder12 and the original PFN architecture22, but it treats each cell in the table as a separate time position, similar to that in ref. 28. Therefore, it can generalize to more training samples as well as features than seen during training.
Figure 1b details our new architecture. All features that go into our architecture are first mapped to floating point values, that is, categoricals are transformed to integers. These values are subjected to z-normalization using the mean and standard deviation for each feature separately across the whole training set. These values are now encoded with simple linear encoders. Each layer first has an attention over features, followed by an attention over samples, both of which operate separately on each column or row, respectively. These two sub-layers are followed by an MLP sublayer. Each sublayer is followed by a residual addition and a half-precision layer norm.
We found that encoding groups of features can be even more effective compared with encoding one value per representation. For our hyperparameter search space, we selected six architectures for classification and five for regression. In three of the six classification models and four of the five regression models, including the TabPFN default, a transformer position encodes two features of one example; in others, it represents one value.
Although the inter-feature attention is a classical fully connected attention, our inter-sample attention does not allow the test samples to attend to each other but only to the training data. Therefore, we make sure that the test samples do not influence each other or the training set representations. To allow our model to differentiate features more easily that have the same statistics, for example, two features that have the same entries just in different orders, we use random feature embeddings that we add to all embeddings before the first layer. We generate one embedding per feature by projecting a random vector of one-fourth the size of our embeddings through a learned linear layer and add this to all embeddings representing an instance of that feature.
As the representations of training samples are not influenced by the test set, we cache the keys and values of the training samples to allow splitting training and inference. We use a special variant of multi-query attention for our inter-sample attention from test samples56 to save memory when caching representations. In our variant, we use all keys and values for the attention between samples of the training set, but repeatedly use the first key and value for attention from the test samples. This allows caching only one key or value vector pair per cell in the training set that is fed into our inter-sample attention of new test samples.
The compute requirements of this architecture scale quadratically with the number of samples (n) and the number of features (m), that is O(n2 + m2), and the memory requirements scale linearly in the dataset size, O(n ⋅ m).
Finally, we found that pre-processing inputs can help performance, thus we can perform z-normalization of all inputs across the sample dimension and add an extra input for each cell that indicates whether the input was missing; the input itself is set to 0 in these cases. All inputs are finally linearly encoded into the embedding dimension of TabPFN.
Details on the causal generative process
An SCM \(\mathcalG:= (Z,\epsilon )\) consists of a collection Z ≔ (z1, …, zk) of structural assignments (called mechanisms): \(z_i=f_i(z_\rmPA\mathcalG(i),\epsilon _i)\,,\) where \(\rmPA\,\mathcalG(i)\) is the set of parents of node i (its direct causes) in the underlying directed acyclic graph (DAG) \(\mathcalG\) (the causal graph), fi is a (potentially nonlinear) deterministic function and ϵi is a noise variable. Causal relationships in \(\mathcalG\) are represented by edges pointing from causes to effects31. As our prior is a sampling procedure, we can make a lot of choices on, for example, the graph size or complexity. By defining a probability distribution over these hyperparameters in the prior, the posterior predictive distribution approximated by TabPFN at inference time implicitly represents a Bayesian ensemble, jointly integrating over a weighted hyperparameter space. The specific hyperparameter ranges and sampling strategies are chosen to cover a diverse set of scenarios that we expect to encounter in real-world tabular data.
Graph structure sampling
The structural causal models underlying each dataset are based on a DAG \(\mathcalG\). We sample these graphs using the growing network with redirection sampling method57, a preferential attachment process that generates random scale-free networks. We either sample a single connected component or merge multiple disjoint subgraphs. Disjoint subgraphs lead to features that are marginally independent of the target if they are not connected to the target node, reflecting real-world scenarios with uninformative predictors.
To control the complexity of the sampled DAGs, we use two hyperparameters: the number of nodes N and the redirection probability P. N is sampled from a log-uniform distribution, \(\log N \sim \mathcalU(a,b)\), where a and b are hyperparameters controlling the range of the graph size. The redirection probability P is sampled from a gamma distribution, P ~ Γ(α, β), where α and β are shape and rate parameters, respectively. Larger values of N yield graphs with more nodes, whereas smaller values of P lead to denser graphs with more edges on average57.
Computational edge mappings
In our implementation, each SCM node and sample is represented as a vector in \(\mathbbR^d\). When propagating data through the SCM, the deterministic functions fi at each edge map the input vectors to an output vector using four types of computational modules:
-
1.
Small neural networks: here we initialize weight matrices \(W\in \mathbbR^d\times d\) using Xavier initialization58 and apply a linear transformation Wx + b to the input vectors \(x\in \mathbbR^d\), where \(b\in \mathbbR^d\) is a bias vector. After the linear projection, we apply element-wise nonlinear activation functions \(\sigma :\mathbbR^d\to \mathbbR^d\), randomly sampled from a set, including identity, logarithm, sigmoid, absolute value, sine, hyperbolic tangent, rank operation, squaring, power functions, smooth ReLU59, step function and modulo operation.
-
2.
Categorical feature discretization: to generate categorical features from the numerical vectors at each node, we map the vector to the index of the nearest neighbour in a set of per node randomly sampled vectors p1, …, pK for a feature with K categories. This discrete index will be observed in the feature set as a categorical feature. We sample the number of categories K from a rounded gamma distribution with an offset of 2 to yield a minimum number of classes of 2. To further use these discrete class assignments in the computational graph, they need to be embedded as continuous values. We sample a second set of embedding vectors \(\p_1^\prime ,\ldots ,p_K^\prime \\) for each class and transform the classes to these embeddings.
-
3.
Decision trees: to incorporate structured, rule-based dependencies, we implement decision trees in the SCMs. At certain edges, we select a subset of features and apply decision boundaries on their values to determine the output60. The decision tree parameters (feature splits, thresholds) are randomly sampled per edge.
-
4.
Noise injection: at each edge, we add random normal noise from the normal distribution \(\mathcalN(0,\sigma ^2I)\).
Initialization data sampling
For each to-be-generated sample, we randomly generate initialization data ϵ that is inserted at the DAG root nodes and then propagated through the computational graph. The noise variables ϵ are generated according to one of three sampling mechanisms:
-
1.
Normal: \(\epsilon \sim \mathcalN(0,\sigma _\epsilon ^2)\), where \(\sigma _\epsilon ^2\) is a hyperparameter.
-
2.
Uniform: \(\epsilon \sim \mathcalU(-a,a)\), where a is a hyperparameter.
-
3.
Mixed: for each root node, we randomly select either a normal or uniform distribution to sample the initialization noise ϵ from.
Furthermore, we sample input data with varying degrees of non-independence for some datasets. Here we first sample a random fraction ρ of samples to serve as prototypes \(x_1^* ,\ldots ,x_M^* \), where M = ρn and n is the dataset size. Then, for each input vector xi to be sampled, we assign weights αij to the prototypes and linearly mix the final input as
$$x_i=\mathop\sum \limits_j=1^M\alpha _ijx_j^* ,$$
(1)
where ∑jαij = 1. The weights αij are sampled from a multinomial distribution, αi ~ Multinomial(β), where β is a temperature hyperparameter controlling the degree of non-independence: larger β yields more uniform weights, whereas smaller β concentrates the weights on fewer prototypes per sample.
Post-processing
Each dataset is post-processed randomly with one or more of the following post-processings: (1) For some datasets, we use the Kumaraswamy feature warping, introducing nonlinear distortions33 to features as done in ref. 61. (2) We quantize some continuous features into buckets of randomly sampled cardinality K, mimicking binned or discretized features commonly encountered in datasets. We map a feature value x to the index of the bucket it falls into, determined by K + 1 bin edges sampled from the set of values this feature takes. (3) To introduce scenarios for dynamic imputation and handling of incomplete datasets, a common challenge in data science, we randomly designate a fraction ρmiss of the data as missing according to the missing completely at random strategy. Each value is masked as missing with probability ρmiss, independently of the data values.
Target generation
To generate target labels for regression tasks, we select a randomly chosen continuous feature without post-processing. For classification labels, we select a random categorical feature that contains up to 10 classes. Thus, natively our method is limited to predicting at most 10 classes. This number can be increased by pre-training on datasets with a larger number of classes or by using approaches such as building a one-vs-one classifier, one-vs-rest classifier or building on approaches such as error-correcting output codes (ECOC)62.
Training details
The training loss of any PFN is the cross-entropy between the targets of held-out samples of synthetic datasets and the model prediction. For a test set (Xtest, ytest) = Dtest, the training loss is given by \(\mathcalL_\rmP\rmF\rmN=\bfE_((\boldsymbolX_\rmt\rme\rms\rmt,\boldsymboly_\rmt\rme\rms\rmt)\cup D_\rmt\rmr\rma\rmi\rmn)\sim p(D)[-\log q_\theta (\boldsymboly_\rmt\rme\rms\rmt|\boldsymbolX_\rmt\rme\rms\rmt,D_\rmt\rmr\rma\rmi\rmn)]\). By minimizing this loss, the PFN learns to approximate the true Bayesian posterior predictive distribution for a chosen prior over datasets (and potentially their latent variables) D, as shown in ref. 22.
We trained our final models for approximately 2,000,000 steps with a batch size of 64 datasets. That means the models used for TabPFN are trained on around 130,000,000 synthetically generated datasets each. One training run requires around 2 weeks on one node with eight Nvidia RTX 2080 Ti GPUs. We sample the number of training samples for each dataset uniformly up to 2,048 and use a fixed validation set size of 128. We sample the number of features using a beta distribution (k = 0.95, b = 8.0) that we linearly scale to the range 1–160. To avoid peaks in memory usage, the total size of each table was restricted to be below 75,000 cells by decreasing the number of samples for large numbers of features.
We chose the hyperparameters for the prior based on random searches, in which we use only a single GPU per training and evaluate on our development set, see section ‘Quantitative analysis’. We used the Adam optimizer24 with linear warmup and cosine annealing63 and tested a set of learning rates in [0.0001, 0.0005], using the one with the lowest final training loss.
Inference details
To get the most performance out of TabPFN, it is crucial to optimize its inference pipeline. We generally always apply TabPFN in a small ensemble, in which we perform pre-processing or post-processing of the data differently for each ensemble member.
As our models are not fully permutation invariant, for each ensemble member, we shuffle the feature order, approximating order invariance64. For classification tasks, we additionally randomly permute the labels. We also apply a temperature to the softmax distribution of our model outputs for calibration.
Apart from the above, we use a subset of the following for each of our default ensemble members:
-
1.
Quantile + Id: we quantize the inputs to equally spaced values between 0 and 1, but keep a copy of each original feature. This effectively doubles the number of features passed to TabPFN.
-
2.
Category shuffling: the labels of categorical features with low cardinality are shuffled.
-
3.
SVD: an SVD compression of the features is appended to the features.
-
4.
Outlier removal: all outliers, more than 12 standard deviations from the mean, are removed.
-
5.
Power transform: each feature (or the label for regression) is transformed using a Yeo–Johnson transformation to stabilize the variance and make the data more normally distributed.
-
6.
One-hot encoding: categorical features are encoded using one-hot encoding, in which each category is represented as a binary vector.
For PHE and hyperparameter tuning of TabPFN, we use a larger set of pre-processing techniques that additionally include a logarithmic, an exponential and a KDI transformation65. These transformations help address nonlinear relationships, skewed distributions and varying scales among features.
To calibrate prediction uncertainty, we apply a softmax temperature (default T = 0.9) by dividing logits before the softmax calculation:
$$P(y_i| x)=\frac\exp (z_i/T)\sum _j\exp (z_j/T),$$
(2)
where zi are the logits, T is the temperature and P(yi∣x) is the calibrated probability. We offer the option to generate second-order polynomial features by multiplying up to 50 randomly selected feature pairs:
$$f_ij=x_i\cdot x_j,\quad \,\rmfor\,(i,j)\in \mathcalS,$$
(3)
where \(\mathcalS\) is the set of randomly chosen feature pairs. This can capture nonlinear interactions between features. This option is disabled by default. To ensure proper handling of duplicate samples given the sample permutation invariance of our architecture, we add a unique sample identifier feature. This is a random number drawn from a standard normal distribution, ensuring each sample is treated distinctly in the attention mechanism. We also provide an option for subsampling in each estimator, to increase ensemble diversity, which performs random sampling without replacement. This option is disabled by default.
Regression details
To enable our model to do classification on a large range of scales and target distributions, we use the following approach. During pre-training, we rescale our regression targets to have zero mean and a standard deviation of 1 (z-score). To decide where the borders between our features lie, we draw a large sample of datasets from our prior and choose the 1/5,000 quantiles from this distribution. At inference time, we bring the real-world data to a similar range by again applying z-score normalization. Furthermore, we allow applying a range of transforms, including a power transform as part of our default. All of the transforms, including the z-score are inverted at prediction time by applying the inverse of the transform to the borders between buckets. This is equivalent to applying the inverse of the transform to the random variable represented by our output distribution but for the half-normals used on the sides for full support22. This is because all transforms are strictly monotone and the borders represent positions on the cumulative distribution function.
Data grouping based on random forest
To perform well on very heterogeneous datasets, we also propose to use random trees to split the training data into smaller more homogeneous datasets. This technique is used only when performing HPO or PHE for TabPFN. It is especially useful for TabPFN as our model performs best on small datasets.
The pre-processing for a single ensemble member, that is, a single tree, works as follows: we use a standard random tree with feature and sample bootstrapping and Gini impurity loss. For each leaf node of the decision tree, we store the subset of training samples that fall into that node and train a TabPFN on these. To predict the class label for a test sample x, we determine the TabPFN to use by passing x through the decision tree. We set the minimal leaf size to be large (500–2,000) such that the resulting data groups are large enough to train a strong model.
TabPFN (PHE)
To further enhance the inference performance of TabPFN, in TabPFN (PHE), we use PHE for a fixed portfolio of TabPFN configurations from our search space detailed in Extended Data Table 5. For TabPFN (PHE), we first use holdout validation to sequentially evaluate models from the portfolio until a time limit is reached. After all models are evaluated once, we repeat holdout validation with new data splits until the time limit is reached. Then, we ensemble all evaluated TabPFN models by aggregating their predictions with a weighted arithmetic mean. We learn the weights using greedy ensemble selection (GES)42,66 with 25 iterations on prediction data from holdout validation. Finally, we prune each zero-weighted model, refit all remaining models on all data and return the weighted average of their predictions.
Following standard practice in AutoML, we use GES because its predictive performance is often superior to the best individual model43,67,68,69. Owing to its ICL, we expect TabPFN to overfit the training data less than predictions of traditionally trained algorithms; thus, we opt for (repeated) holdout validation (as in Auto-Sklearn 1; ref. 67) instead of (repeated) cross-validation (as in AutoGluon40). Moreover, as GES usually produces sparse weight vectors43,69, we expect the final ensemble after pruning each zero-weighted model to consist of a smaller number of models than for other ensembling approaches, such as bagging. Consequently, PHE can also improve the inference efficiency of a TabPFN ensemble compared with other ensembling approaches.
Foundation model abilities
Density estimation
The combination of a regression and a classification TabPFN can be used as a generative model for tabular data, not only modelling targets but features as well. Let \(\mathcalD=\(\bfx_i,y_i)\_i=1^N\) denote the original dataset, where \(\bfx_i\in \mathbbR^d\) is a d-dimensional feature vector and yi is the corresponding target value, and let qθ represent our trained TabPFN model, either a regression or classification model depending on the target type. We aim to approximate the joint distribution of a new example and its label \(p(\bfx,y| \mathcalD)\). To do this, we factorize the joint distribution as
$$p(\bfx,y| \mathcalD)=\mathop\prod \limits_j=1^dp(x_j| \bfx_ < j,\mathcalD)\cdot p(\,y| \bfx,\mathcalD)$$
(4)
$$\approx \mathop\prod \limits_j=1^dq_\theta (x_j| \boldsymbolx_ < j,\mathcalD_:, < j)\cdot q_\theta (\,y| \boldsymbolx,\mathcalD),$$
(5)
where we only condition on a subset of the features in the training set (\(\mathcalD_:, < j\)). The feature order of the joint density factorization influences the estimated densities. To reduce variance from this source, we apply a permutation sampling approximation of Janossy Pooling at inference time, in which we average the outputs of Nj feature permutations, with Nj = 24 in our experiments64.
As we cannot condition on an empty feature set for technical reasons, we condition the prediction of the first feature x1, on a feature with random noise, that is, no information.
The above factorization of the density of a sample (equation (5)) is completely tractable and we thus use it to estimate the likelihood for data points. This enables tasks such as anomaly detection and outlier identification.
Synthetic data generation
We can leverage the generative abilities of TabPFN (see section ‘Density estimation’) to synthesize new tabular data samples that mimic the characteristics of a given real-world dataset, by simply following the factorization in equation (5) and sampling each feature step by step. The generated synthetic samples (x*, y*) can be used for various purposes, such as data augmentation, privacy-preserving data sharing and scenario simulation.
Embeddings
TabPFN can be used to retrieve meaningful feature representations or embeddings. Given a dataset \(\mathcalD=\(\bfx_i,y_i)\_i=1^N\), the goal is to learn a mapping \(f_\theta :\mathbbR^d\to \mathbbR^k\) that transforms the original d-dimensional feature vectors xi into an embedding space of dimension k. The resulting embeddings \(f_\theta (\bfx_i)\in \mathbbR^k\) capture the learned relationships between features and can be used for downstream tasks. To use TabPFN for this problem, we simply use the target-column representations of its final layer as embeddings.
Detailed evaluation protocol
To rigorously assess the performance and robustness of TabPFN, we conduct a comprehensive quantitative evaluation on standard tabular dataset benchmarks, comparing against state-of-the-art baselines under a standardized protocol.
Default configuration of TabPFN
Unlike traditional algorithms, in-context-learned algorithms do not have hyperparameters that directly control their training procedure. Instead, hyperparameters for inference of TabPFN only control the pre-processing of data and post-processing of predictions (for example, feature scaling or softmax temperature). Our default configuration (TabPFN (default)) for both classification and regression is optimized for accurate predictions with minimal fitting time. Here, we apply the same model multiple times with different pre- and post-processors and take the average over the predictions, yielding a four-way (eight-way for regression) ensemble. The settings for our data processing were obtained through a hyperparameter search optimized on our development datasets. The exact settings chosen are listed in Extended Data Table 5. We emphasize that, as for other foundation models (such as GPT), we trained our TabPFN model once and used the same model to perform ICL in a forward pass on all new datasets.
Baselines
We compare with tree-based methods, such as random forests38, XGBoost7, CatBoost9 and LightGBM8, the state of the art for experts to perform predictions on tabular data14,15. We also compare with simpler methods, such as ridge regression70, logistic regression and SVMs39. Although standard neural networks, which unlike TabPFN do not use ICL, were shown to underperform for small (<10,000 samples) tabular data1,14,71, as a point of reference, we still consider a simple neural network, the MLP.
Tabular dataset benchmarks
We perform our analysis on two widely used and publicly available benchmark suites: the standard AutoML benchmark36 and the recent regression benchmark OpenML-CTR23 (ref. 37). Both benchmarks comprise a diverse set of real-world tabular datasets, carefully curated to be representative of various domains and data characteristics. The authors of the benchmark suite selected these datasets based on criteria such as sufficient complexity, real-world relevance, absence of free-form text features and diversity of problem domains.
For our quantitative analysis of TabPFN for classification tasks, we use a set of test datasets comprising all 29 datasets from the AutoML benchmark with up to 10,000 samples, 500 features and 10 classes. For regression tasks, the AutoML benchmark contains only 16 datasets matching these constraints. To increase statistical power, we augmented this set with all datasets matching our constraints from the recent OpenML-CTR23 benchmark, yielding a test set of 28 unique regression datasets in total. Extended Data Tables 3 and 4 provide full details for our test sets of classification and regression datasets, respectively.
We further evaluated additional benchmark suites from refs. 14,15. In ref. 14, there are 22 tabular classification datasets selected based on criteria such as heterogeneous columns, moderate dimensionality and sufficient difficulty. In ref. 15, there is a collection of 176 classification datasets, representing one of the largest tabular data benchmarks. However, the curation process for these datasets may not be as rigorous or quality controlled as for AutoML Benchmark and OpenML-CTR23. We also evaluated five Kaggle competitions with less than 10,000 training samples from the latest completed Tabular Playground Series.
Development datasets
To decide on the hyperparameters of TabPFN, as well as our hyperparameter search spaces, we considered another set of datasets, our development datasets. We carefully selected datasets to be non-overlapping with our test datasets described above. The list of development datasets can be found in Supplementary Tables 5 and 6. We considered the mean of normalized scores (ROC/RMSE) and rank quantiles and chose the best model configurations on these development datasets.
Metrics and cross-validation
To obtain scores for classification tasks, we use two widely adopted evaluation metrics: ROC AUC (One-vs-Rest) and accuracy. ROC AUC averages performance over different sensitivity–specificity trade-offs, and accuracy measures the fraction of samples labelled correctly.
For regression tasks, we use R2 and negative RMSE as evaluation metrics. R2 represents the proportion of variance in the target column that the model can predict. RMSE is the root of the average squared magnitude of the errors between the predicted and actual values. As we use negative RMSE, for all our four metrics higher values indicate a better fit.
To increase statistical validity, for each dataset and method in our test datasets, we evaluated 10 repetitions, each with a different random seed and train–test split (90% train and 10% test samples; all methods used the same cross-validation splits, defined by OpenML72). We average the scores of all repetitions per dataset. Then, to average scores across datasets, we normalize per dataset following previous benchmarks36,40. The absolute scores are linearly scaled such that a score of 1.0 corresponds to the highest value achieved by any method on that dataset, whereas a score of 0 represents the lowest result. This normalization allows for building meaningful averages across datasets with very different score ranges. We provide absolute performance numbers in Supplementary Data Tables 1–2. All confidence intervals shown are 95% confidence intervals.
We tuned all methods with a random search using five-fold cross-validation with ROC AUC/RMSE up to a given time budget, ranging from half a minute to 4 h. The first candidate in the random search was the default setting supplied in the implementation of the method and was also used if not a single cross-validation run finished before the time budget was consumed. See the section ‘Qualitative analysis’ for the used search spaces per method. All methods were evaluated using 8 CPU cores. Moreover, TabPFN makes use of a 5-year-old consumer-grade GPU (RTX 2080 Ti). We also tested GPU acceleration for the baselines. However, as Extended Data Fig. 2 shows, this did not improve performance, probably because of the small dataset sizes.