Derivations
Derivations for equations (8) and (9) were as follows. The commutator between \(\widehate_ij\) and \(\widehat\psi _k,b^\pm \) is
$$\beginarrayl[\widehate_ij,\widehat\psi _k,b^+]\,=\,\sum _a(\widehat\psi _i,a^+\widehat\psi _j,a^-\widehat\psi _k,b^+-\widehat\psi _k,b^+\widehat\psi _i,a^+\widehat\psi _j,a^-)\\ \,\,\,\,=\,\sum _a\widehat\psi _i,a^+\left(\sum _c,dR_bd^ac\widehat\psi _k,c^+\widehat\psi _j,d^-+\delta _jk\delta _ab\right)-\sum _a\widehat\psi _k,b^+\widehat\psi _i,a^+\widehat\psi _j,a^-\\ \,\,\,\,=\,\sum _a,c,d(R_bd^ac\widehat\psi _i,a^+\widehat\psi _k,c^+)\widehat\psi _j,d^-+\delta _jk\widehat\psi _i,b^+-\sum _a\widehat\psi _k,b^+\widehat\psi _i,a^+\widehat\psi _j,a^-\\ \,\,\,\,=\,\delta _jk\widehat\psi _i,b^+\,,\endarray$$
(20)
in which in the second (third) line we used the first (second) line of equation (6). Similarly, we have
$$[\widehate_ij,\widehat\psi _k,b^-]=-\delta _ik\widehat\psi _j,b^-.$$
(21)
Now we can compute the commutator
$$\beginarrayl[\widehate_ij,\widehate_kl]\,=\,\sum _b[\widehate_ij,\widehat\psi _k,b^+]\widehat\psi _l,b^-+\sum _b\widehat\psi _k,b^+[\widehate_ij,\widehat\psi _l,b^-]\\ \,\,\,\,=\,\sum _b\delta _jk\widehat\psi _i,b^+\widehat\psi _l,b^–\sum _b\widehat\psi _k,b^+\delta _il\widehat\psi _j,b^-\\ \,\,\,\,=\,\delta _jk\widehate_il-\delta _il\widehate_kj\,,\endarray$$
(22)
in which in the second line we used equations (20) and (21).
Exact solution of free paraparticles
Here we present details for solving the general bilinear Hamiltonian in equation (15). Analogous to usual free bosons and fermions, we consider U(N) transformations of \(\\widehat\psi _i,a^\pm \\):
$$\beginarrayl\widehat\psi _i,a^-\,=\,\mathop\sum \limits_k=1^NU_ki^* \widetilde\psi _k,a^-\,,\\ \widehat\psi _i,a^+\,=\,\mathop\sum \limits_k=1^NU_ki\widetilde\psi _k,a^+\,,\endarray$$
(23)
in which Uki is an N × N unitary matrix and we use operators with a tilde \(\widetilde\psi _k,a^\pm \) to denote eigenmode operators. Inserting equation (23) into equation (6), we see that the operators \(\\widetilde\psi _k,a^\pm \\) satisfy exactly the same CRs as \(\\widehat\psi _i,a^\pm \\). Notice that most of our discussions on the second quantization formulation and the state space only assume the CRs in equation (6), so the results obtained for \(\\widehat\psi _i,a^\pm \\) (in particular, the Lie algebra of bilinear operators and the structure of the state space) must also apply to \(\\widetilde\psi _k,a^\pm \\).
Inserting equation (23) into equation (15), we obtain
$$\hatH=\sum _\beginarrayc1\le k,p\le N\\ 1\le a\le m\endarrayh_kp^\prime \mathop\psi \limits^ \sim _k,a^+\mathop\psi \limits^ \sim _p,a^-\equiv \sum _1\le k,p\le Nh_kp^\prime \mathope\limits^ \sim _kp\,,$$
(24)
in which \(h_kp^\prime =\sum _1\le i,j\le NU_kih_ijU_pj^* =[UhU^\dagger ]_kp\). We can therefore choose the unitary matrix U such that \(h_kp^\prime =\epsilon _k\delta _kp\), in which \(\\epsilon _k\_k=1^N\) are eigenvalues of hij. With this choice, the Hamiltonian becomes diagonal \(\widehatH=\sum _k=1^N\epsilon _k\widetilden_k\) and its eigenstates can be taken as the common eigenstates \(\left|\genfrac0ex\alpha _1\widetilden_1,\genfrac0ex\alpha _2\widetilden_2,\ldots ,\genfrac0ex\alpha _N\widetilden_N\right\rangle \) (defined in equation (S4) of the Supplementary Information) of the mutually commuting operators \(\\widetilden_k\_k=1^N\), with energy eigenvalues \(E=\sum _k=1^N\epsilon _k\widetilden_k\), in which \(\\widetilden_k\_k=1^N\) are independent non-negative integers and \(1\le \alpha _k\le d_\widetilden_k\) encodes the single-particle exclusion statistics.
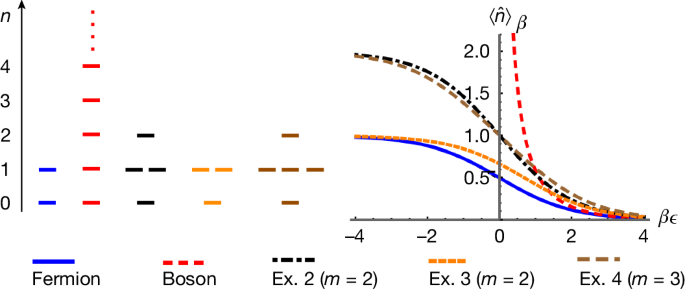
We now calculate physical observables at temperature T. The partition function is a product of single-mode partition functions in equation (12)
$$Z(\beta )\equiv \rmTr[\rme^-\beta \widehatH]=\prod _kz_R(\rme^-\beta \epsilon _k),$$
(25)
so the free energy is
$$F(\beta )=-\frac1\beta \rmlnZ(\beta )=-\frac1\beta \sum _k\rmlnz_R(\rme^-\beta \epsilon _k).$$
(26)
The partition function allows us to compute the thermal average of observables \(\widetilden_k^l\) and \(\widetildee_kp\)
$$\beginarrayl\langle \widetilden_k^l\rangle _\beta \,=\,\frac\rmTr[\widetilden_k^l\rme^-\beta \widehatH]\rmTr[\rme^-\beta \widehatH]=_x=\rme^-\beta \epsilon _k,\\ \langle \widetildee_kp\rangle _\beta \,=\,\delta _kp\langle \widetilden_k\rangle _\beta .\endarray$$
(27)
The thermal average for physical operators \(\widehate_ij\) are obtained by transforming creation and annihilation operators to the eigenmode basis using equation (23) and using the result for \(\langle \widetildee_kp\rangle _\beta \) given in equation (27), which yields
$$\langle \widehate_ij\rangle _\beta =\sum _kU_kiU_kj^* \langle \widetilden_k\rangle _\beta .$$
(28)
The thermal average for other physical observables, including correlation functions in and out of equilibrium, can all be calculated exactly in a similar way.
R matrix for the 2D solvable spin model
In the following, we present a unitary R matrix with trivial exclusion statistics but non-trivial exchange statistics, on which the 2D solvable spin model is based. We define the R matrix with m = 4 in the following way. Let S = 1, 2, 3, 4 and r: S × S → S × S be an injective map defined as
$$r(a,b)=\left(\beginarraycccc43 & 12 & 24 & 31\\ 21 & 34 & 42 & 13\\ 14 & 41 & 33 & 22\\ 32 & 23 & 11 & 44\endarray\right)_ab,$$
(29)
in which we use ab as a shorthand for (a, b). For example, r(1, 1) = (4, 3) and r(3, 2) = (4, 1). The map r in equation (29) satisfies the set-theoretical YBE23
$$r^2=\rmid_S\times S,\,r_12r_23r_12=r_23r_12r_23,$$
(30)
in which in the second equation both sides are injective maps from the set S × S × S to itself, r12 = r × idS and r23 = idS × r. Now we define the R matrix as
$$R| a,b\rangle =-| b^\prime ,a^\prime \rangle \,\forall a,b\in S,$$
(31)
in which (b′, a′) = r(a, b). It then follows from equation (30) that R satisfies the YBE (equation (5)). The single-mode partition function zR(x) of this R matrix is zR(x) = (1 + x)4 (see Supplementary Information), meaning that the exclusion statistics of this type of paraparticles is the same as four decoupled flavours of ordinary fermions. Despite having trivial exclusion statistics, the permutation statistics defined by this R matrix is notably distinct from fermions, as is manifest in the paraparticle exchange process in the 2D solvable spin model that we demonstrate later.
Solvable 2D spin models with emergent free paraparticles
In the following, we present a solvable 2D quantum spin model with emergent free paraparticles, based on the set-theoretical R matrix in equation (29). Here we only sketch the key definitions and the main results; the technical details are found in the Supplementary Information. The model is defined on a square lattice with two types of lattice site and open boundary condition, as shown in Extended Data Fig. 1. The Hamiltonian consists of two parts, \(\widehatH=\widehatH_1+\widehatH_2\),
$$\beginarrayl\widehatH_1\,=\,\sum _\nu \widehatA_\nu +\sum _p\widehatB_p\,,\\ \widehatH_2\,=\,-\sum _\langle ij\rangle \widehath_ij-\sum _l\mu _l\widehaty_l,a^+\widehaty_l,a^-\,,\endarray$$
(32)
in which ν and p denote the shaded and white plaquettes, respectively, l runs over all black dots and ⟨ij⟩ runs over all neighbouring pairs of black dots (each pair appears only once). Here \(\widehath_ij\) is a three-body interaction between the vertices of the triangle containing the directed edge ⟨ij⟩, defined as
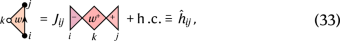
(33)
in which 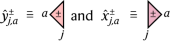 are the same spin operators that appeared in the 1D model, w is one of uL, uR, vL or vR, depending on the type of triangle in the lattice and
are the same spin operators that appeared in the 1D model, w is one of uL, uR, vL or vR, depending on the type of triangle in the lattice and 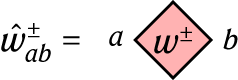 is an operator acting on an auxiliary site (open circles in Extended Data Fig. 1), for a, b = 1,…, 4. The definition of the tensors \(u_L^\pm ,\,u_R^\pm ,\,v_L^\pm \,\rmand\,v_R^\pm \) are given in the Supplementary Information. The operators \(\widehatA_\nu \,\rmand\,\widehatB_p\) in equation (32) are eight-body interaction terms defined as
is an operator acting on an auxiliary site (open circles in Extended Data Fig. 1), for a, b = 1,…, 4. The definition of the tensors \(u_L^\pm ,\,u_R^\pm ,\,v_L^\pm \,\rmand\,v_R^\pm \) are given in the Supplementary Information. The operators \(\widehatA_\nu \,\rmand\,\widehatB_p\) in equation (32) are eight-body interaction terms defined as
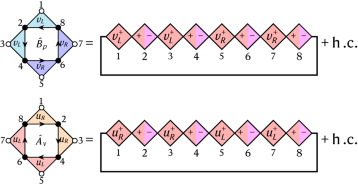
(If a loop term lies on the boundary, then one or more of its white circles will be absent. In this case, the tensors \(u_L^\pm ,\,u_R^\pm ,\,v_L^\pm \,\rmand\,v_R^\pm \) on the absent site is replaced by a δ tensor, that is, \(\widehatw_ab^\pm =\delta _ab\), for w = uL, uR, vL and vR).
The loop terms \(\widehatA_\nu \,\rmand\,\widehatB_p\) are constructed such that they mutually commute and commute with each individual three-body term in \(\widehatH_2\); therefore, they are conserved quantities and eigenstates of \(\widehatH\) can be labelled by their common eigenvalues. In this paper, we are mainly interested in the subspace of states in which all \(\widehatA_\nu \,\rmand\,\widehatB_p\) have minimal eigenvalues (that is, the space of ground states of \(\widehatH_1\)), henceforth referred to as the zero-vortex sector Φ0. The Hilbert space dimension of this sector is 16N, in which N is the total number of black dots in the lattice.
To solve the spectrum in the zero-vortex sector, we define paraparticle creation and annihilation operators by means of a generalized MPO JWT, which generalizes the 1D case given in equation (18). Each paraparticle operator \(\widehat\psi _i,a^\pm \) is defined on a string Γ connecting the lattice origin to the site i, and \(\widehat\psi _i,a^\pm \) is a MPO acting consecutively on all of the black dots on Γ (including the start and end points) and all of the open circles adjacent to Γ; see Extended Data Fig. 1 for an example. The MPO representation of \(\widehat\psi _i,a^\pm \) is similar to the 1D case given in equation (18), but now with the tensors w± inserted between neighbouring T±, in which w is one of uL, vL, uR or vR, depending on the type of triangle between the neighbouring black dots. For example, for the string Γ in Extended Data Fig. 1 that starts at point 0 (lattice origin) and ends at point i, \(\widehat\psi _i,a^\pm \) acts on all of the purple dots and is defined as
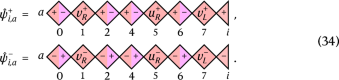
(34)
Paraparticle operators \(\\widehat\psi _i,a^\pm \\) constructed this way have several important properties. First, they commute with all individual terms in \(\widehatH_1\), therefore, their actions leave the zero-vortex sector Φ0 invariant. Second, as shown in the Supplementary Information, although each paraparticle operator \(\widehat\psi _i,a^\pm \) is defined on a specific path, their actions in the zero-vortex sector Φ0 do not depend on the choice of the path, only on the end points. This is because of the special topological property of the zero-vortex sector and is reminiscent of the path independence of the action of the string operators on the toric code ground states30. Finally, in the zero-vortex sector, the operators \(\\widehat\psi _i,a^\pm \\) satisfy the parastatistical CRs in equation (6), justifying their name ‘paraparticle operators’. These properties lead us to Theorem 1 (see also Supplementary Information).
Theorem 1
In the zero-vortex sector, \(\widehatH_2\) is mapped to the free paraparticle Hamiltonian
$$\widehatH_2\,=\,-\sum _\langle ij\rangle ,1\le a\le m(\,J_ij\widehat\psi _j,a^+\widehat\psi _i,a^-+\rmh.c.)-\sum _l\mu _l\widehatn_l.$$
(35)
We expect that our 2D solvable spin models exhibit new chiral and gapless topological phases that are not exhibited by previous solvable models. So far, the only family of solvable models for chiral topological order in 2D is Kitaev’s honeycomb model31 and its generalizations32,33, whose gapped phases are classified by the 16-fold way31, depending on the Chern number (νmod 16) of the free fermion band. We expect that the gapped phases of our model are similarly classified by the Chern number of the free paraparticle band. When ν = 0, both Kitaev’s honeycomb model and our models are in non-chiral quantum double phases, but the former only hosts \(\mathbbZ_2\) abelian anyons, whereas the latter host non-abelian anyons already at ν = 0. We expect that our models host different chiral topological phases also at non-zero ν and different gapless topological phases when the free paraparticles have a gapless spectrum.
Particle exchange statistics in the 2D solvable model
We now illustrate the exchange statistics of the emergent paraparticles in the 2D solvable spin model, which reveals a notable physical difference between the emergent paraparticles and ordinary fermions and bosons.
Consider the paraparticle exchange process described in Extended Data Fig. 2. For simplicity, we consider the case when −μl is large, so that the ground state |G⟩ of the 2D system has no paraparticles, that is, \(\widehatn_l| G\rangle =0\forall l\). At t = 0, we can apply local unitary operators on the ground state |G⟩ to create a paraparticle at sites i and j, respectively, and obtain the state \(| G;ia,jb\rangle \equiv \widehat\psi _i,a^+\widehat\psi _j,b^+| G\rangle \) (see Supplementary Information). Then we evolve the state \(| G;ia,jb\rangle \) with \(\widehatE_ij\), which moves the paraparticles along the coloured paths shown in Extended Data Fig. 2 (\(\widehatE_ij\) can be constructed from a product of local unitaries of the form \(\rme^\rmi\frac\pi 2(\widehate_kl+\widehate_lk)\), in which \(\widehate_kl\) is mapped to a local three-body interaction in the 2D model). The result of this unitary exchange process is given by equation (14), in which |0⟩ is understood as the ground state |G⟩. With the set-theoretical R matrix in equations (29) and (31), the final state is −|G; ib′, ja′⟩, in which (b′, a′) = r(a, b), and the labels a′ and b′ can be locally measured at the two corners (See Supplementary Information). For example, if we start with a = b = 1, we end up measuring b′ = 4 and a′ = 3. That is, the auxiliary space of the paraparticles undergoes a non-trivial unitary rotation even though the two particles stay arbitrarily far apart from each other throughout the whole process. This is in contrast with fermions and bosons, in which case we would measure a′ = a and b′ = b, that is, the indices are simply carried with the particles without any change.
In principle, the exchange process described above can also be done in the 1D spin model in equation (17). In this case, the paraparticles can also be created and measured at the two ends of the open chain, equation (14) still holds and the measurement result is the same. The main difference from the 2D case is that, in 1D, the two paraparticles inevitably collide during the exchange and the exchange statistics results from the interaction between the two paraparticles, which is sensitive to the microscopic details of the exchange operator \(\widehatE_ij\) and is not robust against local perturbations. By contrast, in 2D, the paraparticles can stay far away from each other throughout the exchange and their exchange statistics has a topological nature independent of the detailed shape of the space-time trajectory of the particles and is robust against all local perturbations when the particles are far away from the boundaries and from each other.