Media
LB: 10 g l−1 Bacto-tryptone, 5 g l−1 yeast extract, 10 g l−1 NaCl; autoclaved 20 min at 120 °C. YPDA: 20 g l−1 glucose, 20 g l−1 peptone, 10 g l−1 yeast extract, 40 mg l−1 adenine sulfate; autoclaved 20 min at 120 °C. SORB: 1 M sorbitol, 100 mM lithium acetate, 10 mM Tris pH 8.0, 1 mM EDTA; filter-sterilized (0.2 mm nylon membrane, ThermoScientific). Plate mixture: 40% PEG3350, 100 mM lithium acetate, 10 mM Tris-HCl pH 8.0, 1 mM EDTA pH 8.0; filter-sterilized. Recovery medium: YPD (20 g l−1 glucose, 20 g l−1 peptone, 10 g l−1 yeast extract) + 0.5 M sorbitol; filter-sterilized. SC-URA: 6.7 g l−1 yeast nitrogen base without amino acid, 20 g l−1 glucose, 0.77 g l−1 complete supplement mixture drop-out without uracil; filter-sterilized. SC-URA/ADE: 6.7 g l−1 yeast nitrogen base without amino acid, 20 g l−1 glucose, 0.76 g l−1 complete supplement mixture drop-out without uracil, adenine and methionine; filter-sterilized. MTX competition medium: SD–URA/ADE + 200 μg ml−1 methotrexate (BioShop Canada), 2% DMSO. DNA extraction buffer: 2% Triton X-100, 1% SDS, 100 mM NaCl, 10 mM Tris-HCl pH 8, 1 mM EDTA pH 8.
Library design, synthesis and cloning
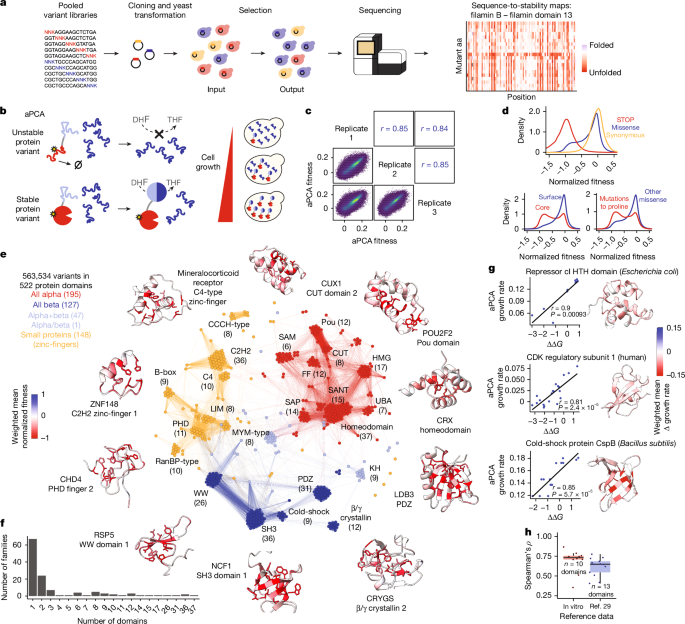
We sampled PFAM-annotated human protein domains (version 34.0) of intracellular human proteins (not defined as ‘extracellular’, ‘transmembrane’ or ‘secreted’ in UniProt), prioritizing proteins that had at least one annotated pathogenic variant in ClinVar3. We additionally included protein domains with in vitro stability measurements to benchmark the assay. We designed the library in two rounds: we first designed and selected two libraries (A1 and B3) containing single mutants of a total of 485 domains that had been previously tested to grow as wild types. To design a second set of libraries (C1 to C7), based on the results of A1 and B3, we excluded domains without a well-defined hydrophobic core (not having at least 10% of residues with rSASA <25%) and disordered domains defined as having an average AlphaFold2 pLDDT < 50, indicative of protein disorder. This second set contained 631 domains that had been previously tested to grow as wild type, and 132 additional domains not previously tested. The domain sequences were codon optimized with emboss backtranseq67 using the Saccharomyces cerevisiae codon usage table, and excluding the GCT alanine codon to prevent the appearance of HindIII restriction sites. The domain sequences were fused to 5′ gggctgctctagaatggctagc and 3′ aagcttggcggtggcgggtctg constant regions containing NheI and HindIII restriction sites for cloning.
Libraries were synthesized by GCATbio using mMPS technology31. The mMPS platform employs a streamlined four-module process—identification, sorting, parallel synthesis, and recycling—to enable an efficient and flexible workflow using traditional phosphoramidite chemistry for oligonucleotide synthesis. Silicon carbide wafers were used as the substrate, with each microchip uniquely engraved with a QR code, serving as both a chip identifier and a record of the predetermined sequence information. This allowed for precise sequence identification and assembly post-synthesis. Standard and degenerate bases (N/K, representing a mixture of A, T, C and G, or T and G, respectively) were employed for synthesis. The degenerate bases were pre-mixed in an optimized ratio to ensure equal representation of each nucleotide at the targeted mutation sites. Library A1, containing sequences shorter than 128 nt, was synthesized using single-stranded oligonucleotides directly cleaved from the microchip. By contrast, the remaining eight libraries (B3, C1 to C7), composed of longer sequences (sequence lengths ranging from 179 to 341 bases), were constructed via polymerase cycling assembly (PCA)-PCR. Initially, the sequences were divided into 378,896 sub-sequences, each ranging from 60 to 80 nt, for synthesis using the mMPS system. The full-length DNA fragments of each library were then assembled from these sub-fragments using PCA-PCR.
Libraries were cloned at a variant coverage of ~100× or greater by restriction digestion and ligation into pGJJ162 (Supplementary Table 6), an aPCA assay plasmid where the DHFR3 fragment is fused at the C terminus of the target protein domains and the fusion is driven by the CYC promoter, and the DHFR1,2 fragment is expressed at high levels as is driven by the GPD promoter.
Large-scale transformation and competition assay
Variant libraries were transformed in triplicate with a coverage of 20× or greater (with a mean coverage across libraries ~170×). For each transformation, we grew a 1 l YPDA culture of late log phase S. cerevisiae BY4741 cells (OD600 ~ 0.8–1), collected the cells by centrifugation (5 min, 4,000g), resuspended in 43 ml SORB medium and incubated for 30 min on a shaker at room temperature. Then, 875 μl of 10 mg ml−1 previously boiled (5 min, 100 °C) single-stranded DNA was added to the cells, followed by 17.5 μg library plasmid DNA and 175 ml plate mixture. The mix was incubated for 30 min on a shaker at room temperature. 17.5 ml DMSO were then added, and the cells were split in 50 ml Falcon tubes for 20 min heat shock at 42 °C. Following incubation, cells were pooled and collected by centrifugation, the supernatant was discarded with a pump, and cells were resuspended in 250 ml recovery medium and incubated at 30 °C for 1 h. Cells were then centrifuged for 3 min at 3,000g and transferred into 1 l SC-URA. Ten microlitres of this culture were immediately plated onto SC-URA selective plates to monitor transformation efficiency. The rest of the culture was incubated for one or two overnights at 30 °C.
SC-URA cultures were used to inoculate a 1 l culture of SC-URA-ADE at an OD600 = 0.2–0.4, which was grown overnight (input culture). Cells from this culture were inoculated in 1 l SC-URA/ADE + 200 μg ml−1 MTX to select stably expressed protein domain variants. The remaining input cells grown SC -URA/ADE were collected and frozen for DNA extraction. MTX cultures were left to grow overnight to an OD600 = 1.6–2.5, corresponding approximately to 5 generations, collected and frozen for DNA extraction (outputs).
DNA extraction, plasmid quantification and sequencing library preparation
Total DNA was extracted from yeast pellets equivalent to 50 ml of cells at OD600 = 1.6 as described in our previous work32,39. Plasmid concentrations in the resulting samples were quantified by against a standard curve of known concentrations by qPCR, using oGJJ152 and oGJJ153 as qPCR primers that amplify in the origin of replication of the aPCA assay plasmid.
To generate the sequencing libraries, we performed two rounds of PCR amplification. In the first round, we used primer pools (oTB595+ and oTB748+; Supplementary Table 7) flanking the inserts that introduce frame-shifting nucleotides between the Illumina adapters and the sequencing region of interest. To maintain variant representation, we carried out eight 100 μl PCR1 reactions per sample, each of which starting with 125 million plasmid molecules that we amplified for 8 cycles. The reactions were column-purified (QIAquick PCR purification kit, QIAGEN), and the purified product was amplified further using the standard i5 and i7 primers to add the remainder of the Illumina adapter sequences and the demultiplexing indices (dual indexing) unique to each sample. We carried out a total of 8 100 μl PCR2 reactions per sample, each starting with 20–40 ng of purified product, that was amplified for 8 more cycles. The resulting amplicons were run on a 2% agarose gel to quantify the samples before pooling them for joint purification, and to ensure the specificity of the amplification and check for any potential excess amplification problems. The final libraries were size selected by electrophoresis on a 2% agarose gel, and gel-purified (QIAEX II Gel Extraction Kit, QIAGEN). The amplicons were subjected to Illumina paired-end 2 × 150 sequencing on a NextSeq2000 instrument at the CRG Genomics facility.
Sequencing data processing and normalization
FASTQ files from paired-end sequencing of all aPCA selections were processed with DiMSum68 v1.2.11 (https://github.com/lehner-lab/DiMSum) using default settings with minor adjustments. The option “barcodeIdentityPath” was used to specify a variants file in order to recover designed variants only (NNK mutations in the protein domains present in each sublibrary), and starting and final culture optical densities and selection times were specified to infer absolute growth rates across libraries.
Data filtering and normalization
We computed several quality control metrics on a per-domain basis. First, the wild-type position in the fitness distribution, as the difference between the wild-type and the 95th percentile of the distribution, divided by the difference between the 95th and 5th percentile in the distribution (fitness 90% range). Second, the Pearson’s correlation coefficient between biological replicates for missense variants. Third, the correlation between fitness and solvent accessibility for all variants in each domain. And fourth, the correlation between fitness and hydrophobicity of all variants in each domain (measured as the first principal component of a comprehensive table of amino acid properties69). All structural calculations of the domains analysed are based on AlphaFold2 predictions obtained from https://alphafold.ebi.ac.uk/.
Compared to folded domains (more than 10% core residues and pLDDT > 50), disordered and domains without a well-defined hydrophobic core (see ‘Library design’) behave in a very distinct fashion in aPCA, with the wild type located in the middle of the fitness distribution, hydrophobicity negatively correlated with protein abundance, and narrow dynamic ranges resulting from typically small effects of mutations (Extended Data Fig. 1c). We thus excluded these domains from further analysis in the main text. Folded domains showed larger dynamic ranges, with the wild-type among the fittest variants, a negative correlation between mutation sensitivity and solvent accessibility, and a lack of correlation to hydrophobicity (Extended Data Fig. 1c). For folded domains, the four quality metrics described above were highly correlated with each other, and we combined them using principal component analysis. The first principal component explained 64% of the variance, and was used as a single quality metric to rank all domains.
We retained all domains ranked 600 or higher, with a missense Pearson’s r > 0.485, and with more than 50% of variants measured (with at least 10 counts in at least 1 replicate), resulting in 538 domains. We removed from this set 16 additional domains that were not compatible with 2-state folding, either showing many large effect abundance-increasing mutations (O75364_PF00046_64, O75956_PF09806_73, P10242_PF00249_89, P52952_PF00046_140, Q13263_PF00643_205, Q86TZ1_PF13181_60, Q8IX03_PF00397_1, Q8NDW8_PF13181_799, Q9Y2H9_PF17820_968, Q9Y6M9_PF05347_15), narrow fitness ranges (P35637_PF00641_421, EHEE-rd2-0005_1, HHH-rd2-0133_1), or clear correlations to hydrophobicity (E9PAV3_PF19026_2040, HEEH-rd3-0223_1, Q5VTD9_PF00096_193), resulting in a final set of 522 domains.
The distributions of quality metrics for retained and discarded folded domains, and for disordered domains and folded domains without a well-defined core are in Extended Data Fig. 1c. Of the 478 discarded folded domains, 224 had slow growth rates as wild type (<0.075 h−1), 176 had an unfit wild type (wild-type position <0.4), 107 were negatively correlated with hydrophobicity (Pearson’s r < −0.25), and 158 were not correlated with solvent accessibility (Pearson’s r < 0) (we note that many of the discarded domains meet more than one of these criteria). Discarded domains are shorter (median length = 49 amino acids (aa)) than retained domains (length = 58 aa, p = 1.87 × 10−14, Wilcoxon rank sum test), and are enriched in zinc-finger domains (57% of zinc-finger domains discarded in contrast to 43%, 41%, and 39% for all-alpha, all-beta, and alpha+beta, respectively, P = 2.33 × 10−6, Fisher’s exact test). Multimerization status only affected success rate marginally, as 49% of domains from proteins that form complexes70 were discarded, compared to 53% of those that do not engage in protein–protein interactions (P = 0.2, Fisher’s exact test). Finally, domains with yeast orthologues71 were less likely to be retained (45%) than domains without yeast orthologues (53%, P = 0.08, Fisher’s exact test).
We normalized the growth rates and growth rate errors within each protein domain by linearly scaling the data such that the wild type-normalized fitness equals zero, and the 2.5th percentile of the distribution of growth rates of all missense variants plus the wild type is equivalent to a normalized fitness of −1. In all box plots shown in the manuscript, the central line represents the median, the upper and lower hinges correspond to the first and third quartiles, with the upper whisker extending from the hinge to the largest value no further than 1.5 × IQR, and the lower whisker extending from the hinge to the smallest value no further than 1.5 × IQR.
Structural similarity network representation
We generated a structural distance matrix based on Foldseek72 hit probabilities. We computed all pairwise alignments between the domains in the final retained set by first creating a Foldseek database ‘foldseek_domainome_db’ containing all domains, and then searching all domains against the database using foldseek easy-search *.pdb foldseek_domainome_db foldseek_easy_allvsall tmp –format-output “query,target,alntmscore,qtmscore,ttmscore,prob” –exhaustive-search TRUE -e inf.
To visualize the similarity network, we imported the domains as nodes and the Foldseek probabilities as edges into Gephi73, and applied two layout algorithms: first the Fruchterman Reingold algorithm to equilibrium, which resulted in a clear separation of the different SCOP classes, followed by a Force Atlas 2 layout algorithm (preventing node overlap), which accentuated the separation between the different domain family clusters within each SCOP class.
Comparison to reference ∆∆G datasets
To compare aPCA measurements with in vitro ∆∆G values, we used domains containing at least 10 variants in more than a single residue measured in vitro and in aPCA, and with a range of at least 2 kcal mol−1 for the in vitro measurements, and of 0.075 h−1 log growth rate units for the aPCA measurements (n = 10 domains). To compare aPCA measurements with ∆∆G values derived from high-throughput proteolysis deep mutational scans29, we used protein domains with an overlap (overlapping length/total alignment length) of at least 80%, and an aPCA measurement range of 0.075 h−1 log growth rate units (n = 12).
The total number of human missense variants measured in the Megascale dataset29 was retrieved from the high-confidence dataset excluding double mutants and domain duplicates (from different Protein Data Bank (PDB) entries and genetic backgrounds of the same PDB entry). We also quantified the total number of human missense variants measured in all abundance (VAMP-seq, aPCA) datasets available (as of 7 July 2024) in MaveDB66 total number of human missense variants in ProthermDB33.
Comparison to VEPs
We generated ESM1v12 predictions (https://github.com/facebookresearch/esm) using the domain sequences alone as input, and using sliding windows across the human proteome (size = 1,000 aa, step = 250 aa). For each domain, we used the predictions corresponding to the window in which the domain is most centred. We obtained precomputed AlphaMissense11,12,13,14 predictions from https://console.cloud.google.com/storage/browser/dm_alphamissense. We obtained EVE11, popEVE74 and Tranception13 precomputed scores from https://pop.evemodel.org/. ‘EVE domain’ scores computed on high-coverage alignments generated specifically for domainome domains were kindly shared by A. Kollasch and D. Marks. We used precomputed RaSP scores75, and generated DDMut76 and ThermoMPNN35 predictions with the aid of AlphaFold2 structure predictions. FoldX77 predictions were obtained from https://ftp.ebi.ac.uk/pub/databases/ProtVar/predictions/stability/70. We used Spearman’s ρ to quantify the relationship between the predictions and aPCA fitness. Domains with homology to protein domains in the Megascale dataset were defined using hmmer (http://hmmer.org/) hmmscan against PFAM, and predictors were evaluated on a homologue-free set to prevent leakage from ThermoMPNN training.
To estimate the fraction of the variance in mutational effects on evolutionary fitness that are attributable to protein stability, we calculated the correlation between ESM1v fitness predictions on full-length protein sequences and aPCA scores. The correlation coefficient was adjusted by the measurement error of the aPCA scores according to the Spearman disattenuation formula:
$$R_xy=\fracr_xy\sqrtr_xx$$
where Rxy is the disattenuated correlation coefficient, rxy is the observed correlation coefficient, rxx is the mean correlation coefficient between aPCA biological replicates. This procedure was applied to both linear (Pearson’s) and rank (Spearman’s) correlation coefficients. The two were highly correlated (r = 0.94) and we report the Pearson’s r-based version for ease of interpretation.
Analysis of functional sites
We carried out this analysis for domains where (1) the wild type is above the 30th percentile in the fitness distribution; and (2) the range between the 5th and 95th percentile of the distribution of ESM1v-predicted fitness is greater than 10 (n = 426 domains). We used sigmoid curves to model the relationship between normalized aPCA fitness (stability) and predicted function (ESM1v) of all variants in each individual domain, with an upper bound of 0 (wild-type aPCA-normalized fitness) and a lower bound of −1:
$$f_\rmaPCA=-1+\frac1{1+e^-(f_\rmESM1v-\rmxmid)/\rmscal}$$
Where faPCA is the aPCA-normalized fitness, fESM1v is the ESM1v-predicted fitness, xmid is the midpoint of the sigmoid and scal is the steepness parameter. To prioritize fitting the low stability variants, we weighted the fit by the aPCA-normalized fitness:
$$w_i=(\max (f_\rmaPCA)-\min (f_\rmaPCA)-(f_\rmaPCA,i+1))^2$$
We used a two-tailed z-test to identify mutations whose effects on fitness cannot be accounted for by stability effects. We calculated z-scores as the aPCA residuals to the fit divided by the aPCA error, derived P values based on the normal distribution, and performed multiple testing correction using Benjamini–Hochberg’s FDR. We additionally calculated per-residue mean residuals weighted by the aPCA-normalized fitness error.
We obtained residue-level functional site annotations corresponding to the CDD78 using the InterPro API. Second-shell residues were defined as those with a minimum heavy atom distance of 5 Å to functional site residues.
Analysis of the stability effects of pathogenic variants
We identified destabilizing variants using a one-tailed z-test. z-Scores were calculated as the normalized fitness divided by the normalized fitness error, a P value was derived on the basis of a normal distribution, and FDR multiple test correction was applied. Destabilizing variants were defined as variants with FDR < 0.1, and strongly destabilizing variants as FDR < 0.1 and a normalized aPCA fitness < − 0.3. We obtained clinical variant annotations from ClinVar (January 2024 version) and from the UniProt API. Variant annotations were highly consistent between the two sources, and were merged. We tested for enrichments of clinical variant classes in stability classes using a two-tailed Fisher’s exact test.
To estimate to what extent destabilization explains pathogenic mutations in individual domains, we used MCC. To increase statistical power, we included gnomAD variants with an allele frequency >10−5 as benign. We estimated the errors in MCCs by resampling the dataset based on the mean and errors of aPCA scores, 10 times. To analyse the distribution of pathogenic mutations in the MECP2 methyl-binding domain and the CRX homeodomain, we generated AlphaFold3 predictions79. The sequences of the domains and DNA strands used for the predictions are available as Supplementary Table 8. DNA-binding interface residues were defined using getcontacts80, and second-shell residues were defined as those with a minimum heavy atom distance of 5 Å to binding interface residues.
To extend the analysis to a larger number of domains with small numbers of pathogenic variants, we used the fraction of variance in ESM1v-predicted fitness explained by aPCA scores as described above. MCCs based on clinical and gnomAD variants correlated well with the fraction of evolutionary fitness explained by stability effects in domains with at least 20 clinical and gnomAD variants (r = 0.78), validating the approach. We estimated errors in MCCs by resampling the aPCA fitness dataset using the mean and error of each variant, and recalculating the MCCs on clinical variants (n = 10 samples). To further validate the estimates of the contribution of stability to fitness, we estimated the fraction of variance in ESM1v-predicted fitness explained by thermoMPNN predicted stabilities for non-zinc-finger domains with at least 1 pathogenic variant (n = 86). These correlated well with the original estimates derived using our abundance data (Pearson’s r = 0.81; Extended Data Fig. 2d).
Modes of inheritance and mechanisms of disease information were obtained from OMIM (https://www.omim.org/). To analyse the contribution of stability changes to disease according to mode of inheritance and mechanism of action controlling for protein composition (Extended Data Fig. 4e), we modelled the contribution of secondary structure and the percentage of core residues to the scores using linear models. We then extracted the model residuals as the composition-corrected scores.
Clinical variant classification performance comparisons
We used the pROC R package81 to generate receiver operating characteristic (ROC) curves and calculate ROC area under the curve. We incorporated gnomAD variants with an allele frequency >10−5 as benign. To test the performance when combining structural and sequence features (secondary structure, rSASA, wild-type residue, mutated residue), ESM1v and aPCA scores, we used generalized linear models in R. In addition to training and evaluating on the full dataset, we trained the logistic regression models with 90% of the data and evaluated on the remaining 10% unseen data.
Thermodynamic modelling of protein domain families
We used MoCHI82 to fit 2-state thermodynamic models on a per-family basis (for families with at least 5 human homologues and variants with a mean count >29). We specified a neural network architecture consisting of a single additive trait layer for shared folding energies across the family and a shared linear transformation layer. We used a ‘TwoStateFractionFolded’ transformation derived from the Boltzmann distribution function that relates energies to proportions of folded protein. To map homologous positions across families, we used PFAM alignments of human domains. To input into MoCHI, we recoded each domain wild-type sequence as an indel sequence as long as the PFAM alignment, plus additional positions in the alignment with variants that encode the wild-type identity of each homologue. Mutations in each domain were encoded in the corresponding alignment position. This design allows MoCHI’s one-hot encoding of both the mutations and the wild-type identities simultaneously, and the joint fitting of mutation ∆∆G and starting ∆G of each homologue. We trained the model using a tenfold cross-validation approach and evaluated the performance on held-out data.
We additionally fitted a linear model, and a ‘TwoStateFractionFolded’ model with shared energies across all homologues of a family but with domain-specific linear transformations that account for potential differences in solubility of the folded and unfolded states between domains of the same family. These models resulted in highly correlated inferred energies to the original Boltzmann model (Pearson’s r = 0.972 for the linear model, and r = 0.938 for the Boltzmann model with domain-specific linear transformations) and similar performances on held-out data across families. We discarded the linear model due to highly biased residuals, and chose the ‘TwoStateFractionFolded’ model without homologue-specific linear scaling as the simplest of the remaining models. To compare across protein families, energies were rescaled such that the 2.5th percentile of the distribution of energies is equivalent to a scaled ∆∆G = −1 and the wild type to a ∆∆G = 0.
We further evaluated the performance of the TwoStateFractionFolded model in families with at least ten homologues by training the model leaving out a single domain at a time. The genetic distance (hamming distance and BLOSUM62 distance) of each left-out homologue to each of the homologues that went into training was calculated and averaged, to compare to model performance. The fraction of explainable variance in aPCA scores accounted for by the models was estimated as the R2 between observed and predicted fitness divided by the R2 between replicates.
Epistasis analysis of protein domain families
We identified epistatic variants with large residuals to the MoCHI fits using a two-tailed z-test. We calculated z-scores as the residuals to the fit divided by the aPCA fitness errors, derived P values on the basis of a normal distribution, and applied FDR multiple testing correction. Epistatic mutations were defined as those with |residual| > 0.05 and FDR < 0.1. Enrichments of alignment sites in epistatic variants were calculated, and significantly enriched sites were identified using a two-tailed Fisher’s exact test. Epistatic sites were defined as those with a log2(OR) > 1.5 and a Fisher’s Exact test FDR < 0.05. We classified alignment sites as core residues (rSASA <25% in at least 75% of homologues), surface residues (rSASA > 25% in at least 75% of homologues), or changing residues (the rest). We defined contacts using getcontacts80.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.