Nonlinear receptive fields evoke redundant retinal coding of natural scenes

Tissue preparation and electrophysiology

We recorded spiking activity from retinas of three adult male marmoset monkeys (Callithrix jacchus), 12, 13 and 18 years of age, using a single piece of retina from each animal. No previous determination of sample size was used. The retinal tissue was obtained immediately after euthanasia from animals used by other researchers, in accordance with national and institutional guidelines and as approved by the institutional animal care committee of the German Primate Center and by the responsible regional government office (Niedersächsisches Landesamt für Verbraucherschutz und Lebensmittelsicherheit, permit number 33.19-42502-04-20/3458). After enucleation, the eyes were dissected under room light, and the cornea, lens and vitreous humour were carefully removed. The resulting eyecups were then transferred into a light-tight container containing oxygenated (95% O₂ and 5% CO₂) Ames’ medium (Sigma-Aldrich) supplemented with 4 mM D-glucose (Carl Roth) and buffered with 20–22 mM NaHCO₃ (Merck Millipore) to maintain a pH of 7.4. The container was gradually heated to 33 °C, and after at least an hour of dark adaptation, the eyecups were dissected into smaller pieces. All retina pieces used in this study came from the peripheral retina (7–10 mm distance to the fovea). The retina was separated from the pigment epithelium just before the start of each recording. All reported marmoset data are from pieces for which a 5% contrast full-field modulation at 4 Hz produced at least a 10 spikes per second modulation in the average ON parasol spike rate. This ensured high quality and light sensitivity of the analysed retina pieces (Extended Data Fig. 12).

We also recorded spiking activity from 12 retina pieces of eight wild-type female mice (C57BL/6J) between 7 and 15 weeks old (except for one 23-week-old mouse). No previous determination of sample size was used. All mice were housed on a 12-hour light/dark cycle. The ambient conditions in the animal housing room were kept at around 21 °C (20–24 °C) temperature and near 50% (45–65%) humidity. Experimental procedures were in accordance with national and institutional guidelines and approved by the institutional animal care committee of the University Medical Center Göttingen, Germany. We cut the globes along the ora serrata and then removed the cornea, lens and vitreous humour. The resulting eyecups were hemisected to allow two separate recordings. On the basis of anatomical landmarks, we performed the cut along the horizontal midline and marked dorsal and ventral eyecups. Before the start of each recording, we isolated retina pieces from the sclera and pigment epithelium.

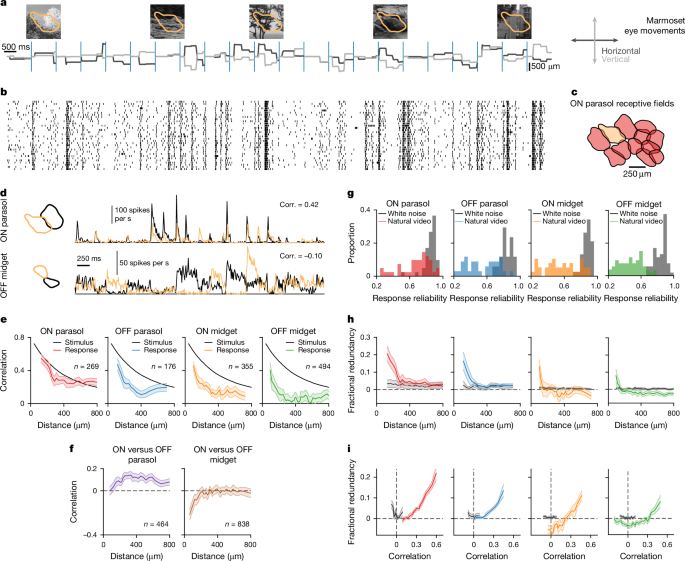
For both marmoset and mouse retina recordings, we placed retina pieces ganglion-cell-side-down on planar multielectrode arrays (Multichannel Systems; 252 electrodes; 10 or 30 μm electrode diameter, either 60 or 100 μm minimal electrode distance) with the help of a semipermeable dialysis membrane (Spectra Por) stretched across a circular plastic holder (removed before the recording). The arrays were coated with poly-D-lysine (Merck Millipore). For some marmoset recordings, we used 60-electrode perforated arrays⁶¹. Dissection and mounting were performed under infrared light (using LEDs with peak intensity at 850 nm) on a stereo-microscope equipped with night-vision goggles. Throughout the recordings, retina pieces were continuously superfused with oxygenated Ames’ solution flowing at 8–9 ml min^−1 for the marmoset or 5–6 ml min^−1 for the mouse retina. The solution was heated to a constant temperature of 33–35 °C through an inline heater in the perfusion line and a heating element below the array.

Extracellular voltage signals were amplified, bandpass filtered between 300 Hz and 5 kHz and digitized at 25 kHz sampling rate. We used Kilosort⁶² for spike sorting. To ease manual curation, we implemented a channel-selection step from Kilosort2 by discarding channels that contained only a few threshold crossings. We curated the output of Kilosort through phy, a graphical user interface for visualization and selected only well-separated units with clear refractory periods in the autocorrelograms. In a few cases, we had to merge units with temporally misaligned templates; we aligned the spike times by finding the optimal shift through the cross-correlation of the misaligned templates.

Visual stimulation

Visual stimuli were sequentially presented to the retina through a gamma-corrected monochromatic white organic LED monitor (eMagin) with 800 × 600 square pixels and 85 Hz (marmoset) or 75 Hz (mouse) refresh rate. The monitor image was projected through a telecentric lens (Edmund Optics) onto the photoreceptor layer, and each pixel’s side measured 7.5 μm on the retina or 2.5 μm for some marmoset recordings in which we used a different light-projection setup⁶¹. All stimuli were presented on a background of low photopic light levels, and their mean intensity was always equal to the background. To estimate isomerization rates of photoreceptors, we measured the output spectrum of the projection monitors and the irradiance at the site of the retina and combined this information with the absorbance profile⁶³ and peak sensitivities of the opsins (543–563 nm for different marmoset M-cones and 499 nm for marmoset rods^64,65; 498 nm for mouse rods) and with the collecting areas of photoreceptors, using 0.5 μm² for mouse rods⁶⁶, 0.37 μm² for marmoset cones and 1.0 μm² for marmoset rods, applying here the values from macaque cones and rods^67,68. For the marmoset, the background light intensity resulted in approximately 3,000 photoisomerizations per M-cone per second and approximately 6,000 photoisomerizations per rod per second, and for the mouse, approximately 4,000 photoisomerizations per rod per second. We fine-tuned the focus of stimuli on the photoreceptor layer before the start of each experiment by visual monitoring through a light microscope and by inspection of spiking responses to contrast-reversing gratings with a bar width of 30 μm.

Receptive-field characterization

To characterize functional response properties of the recorded ganglion cells, we used a spatiotemporal binary white-noise stimulus (100% contrast) consisting of a checkerboard layout with flickering squares, ranging from 15 to 37.5 μm on the side in different recordings. The stimulus update rate ranged from 21.25 to 85 Hz. Each stimulus cycle consisted of a varying training stimulus and a repeated test stimulus, with 18–55 cycles presented in total. The training stimulus duration ranged from 45 to 144 s in different experiments. The test stimulus consisted of a fixed white-noise sequence ranging from 16 s to 18 s, which we used here to determine noise entropies and noise correlations.

We calculated spike-triggered averages (STAs) over a 500 ms time window and extracted spatial and temporal filters for each cell as previously described⁶⁹. In brief, the temporal filter was calculated from the average of spatial STA elements whose absolute peak intensity exceeded 4.5 robust standard deviations of all elements. The robust standard deviation of a sample is defined as 1.4826 times the median absolute deviation of all elements, which aligns with the standard deviation for a normal distribution. The spatial receptive field was obtained by projecting the spatiotemporal STA on the temporal filter. We also calculated spike-train autocorrelation functions under white noise, using a discretization of 0.5 ms. For plotting and subsequent analyses, all autocorrelations were normalized to unit sum.

For each cell, a contour was used to summarize the spatial receptive field. We upsampled the spatial receptive field to single-pixel resolution and then blurred it with a circular Gaussian of σ = 4 pixels. We extracted receptive-field contours using MATLAB’s ‘contourc’ function at 25% of the maximum value in the blurred filter. In some cases, noisy STAs would cause the contour to contain points that lay further away from the actual spatial receptive field. Thus, we triaged the contour points and removed points that exceeded 20 robust standard deviations of all distances between neighbours of the points that were used to define the contour. This process typically resulted in a single continuous area without holes. The centre of each receptive field was defined as the median of all contour points, and its area was determined by the area enclosed by the contour.

Ganglion cell type identification

We used responses to a barcode stimulus⁷⁰ to cluster cells into functional types in each single recording. The barcode pattern had a length of 12,750 (or 12,495) µm and was generated by superimposing sinusoids of different spatial frequencies (f) with a 1/f weighting. The constituent sinusoids had spatial frequencies between 1/12,750 (or 1/12,495) and 1/120 μm^−1 (separated by 1/12,750 or 1/12,495 μm^−1 steps, respectively) and had pseudorandom phases. The final barcode pattern was normalized so that the brightest (and dimmest) values corresponded to 100% (and −100%) Weber contrast from the background. The pattern moved horizontally across the screen at a constant speed of 1,275 (or 1,125) μm s^−1, and the stimulus was repeated 10–20 times. Obtained spike trains were converted into firing rates using 20 ms time bins and Gaussian smoothing with σ = 20 ms. We quantified cell reliability with a symmetrized coefficient of determination (R²), as described previously³⁶. We only included cells with a symmetrized R² value of at least 0.1 and that were not putative DS cells (see below).

We used average responses to the barcode stimulus to generate a pairwise similarity matrix, as described previously⁷⁰. We defined the similarity between each pair of cells as the peak of the cross-correlation function (normalized by the standard deviations of the two signals) between the spike rate profiles of the two cells. To obtain a final similarity matrix, we multiplied the entries of the barcode similarity matrix with the entries of three more similarity matrices, obtained from receptive-field response properties. The first two were generated by computing pairwise correlations between both the temporal filters and the autocorrelation functions of each cell. The third one used receptive-field areas and was defined as the ratio of the minimum of the two areas over their maximum (Jaccard index).

We converted the combined similarity matrix to a distance matrix by subtracting each entry from unity. We then computed a hierarchical cluster tree with MATLAB’s ‘linkage’ function, using the largest distance between cells from two clusters as a measure for cluster distance (complete linkage). The tree was used to generate 20–50 clusters; we chose the number depending on the number of recorded cells. This procedure yielded clusters with uniform temporal components and autocorrelations and with minimally overlapping receptive fields but typically resulted in oversplitting functional ganglion cell types. Thus, we manually merged clusters with at least two cells on the basis of the similarity of properties used for clustering and on receptive-field tiling. To incorporate cells that were left out of the clustering because of the barcode quality criterion, we expanded the clusters obtained after merging. An unclustered cell was assigned to a cluster if its Mahalanobis distance from the centre of the cluster was at most 5 but at least 10 for all other clusters. Our method could consistently identify types with tiling receptive fields forming a mosaic over the recorded area. This was generally the case for parasol and midget cells in the marmoset and the different alpha cells in the mouse retina, which are the ones primarily analysed in this work. Note, though, that mosaics are typically incomplete because of missed cells whose spikes were not picked up by the multielectrode array (or not sufficiently strong to allow reliable spike sorting). As is common with this recording technique, missed cells are more frequent for some cell types than for others, and this recording bias renders, for example, midget cell mosaics less complete than those of parasol cells. The present analyses, however, do not rely on the recovery of complete mosaics, as the pairwise investigations of correlation and redundancy only require sufficient sampling of pairs at different distances.

Matching cell types to mouse ganglion cell databases

We validated the consistency of cell type classification by examining cell responses to a chirp stimulus²⁴, which was not used for cell clustering. Light-intensity values of the chirp stimulus ranged from complete darkness to the maximum brightness of our stimulation screen. The stimulus was presented 10–20 times. For the mouse retina, the parameters of the chirp stimulus matched the original description, which allowed us to compare cell responses to calcium traces in a database of classified retinal ganglion cells²⁴. To convert spike rates to calcium signals, we convolved our spiking data with the calcium kernel reported in the original paper. We then computed correlations to the average traces of each cluster in the database.

For some mouse experiments, we also used responses to spot stimuli²³. In brief, we flashed one-second-long spots over the retina at different locations and with five different spot diameters (100, 240, 480, 960 and 1,200 μm). Between spot presentations, illumination was set to complete darkness, and the spots had an intensity of 100–200 photoisomerizations per rod per second. For each cell, we estimated a response centre by identifying which presented spot location yielded the strongest responses when combining all five spot sizes. We only used cells whose estimated response centre for the spots lay no further than 75 μm from the receptive-field centre as determined with white-noise stimulation. To calculate similarities to the cell types in the available database²³, we concatenated firing-rate responses to the five spot sizes and then calculated correlations with the available database templates. We also applied saccade-like shifted gratings to detect image-recurrence-sensitive cells in mouse retinas as previously described^36,71. These cells correspond to the transient-OFFα cells in the mouse retina.

Natural videos, LN model predictions and response correlations

For the marmoset retina, we constructed natural videos in similar fashion as previously done for the macaque retina^30,72. In brief, the videos consisted of 347 grayscale images that were shown for 1 s each and jittered according to measurements of eye movements obtained from awake, head-fixed marmoset monkeys¹⁶ (graciously provided by J. L. Yates and J. F. Mitchell; personal communication). These eye movement data had been collected at a scale of about 1.6 arcmin per pixel, which roughly corresponds to 2.67 µm on the marmoset retina, using a retinal magnification factor of 100 μm deg^−1 (ref. ⁷³). To align the sampled traces with the resolution of our projection system, we adjusted the pixel size of the gaze traces to 2.5 µm when presenting the natural video. We furthermore resampled the original 1,000 Hz gaze traces to produce a video with a refresh rate of 85 Hz. The presented natural video consisted of 30–35 cycles of varying training and repeated test stimuli. Test stimuli consisted of 22 distinct natural images, using the original grayscale images (graciously provided by J. L. Yates and J. F. Mitchell; personal communication) viewed by the marmosets during eye movement tracing (mean intensity −10% relative to background; 38% average contrast, calculated as the standard deviation across all pixels for each image). Each test image was paired with a unique movement trajectory given by the marmoset eye movements. For each training stimulus cycle, we presented 40 images out of the 325 remaining images (sampled with replacement), each paired with a unique movement trajectory. These 325 images were obtained from the van Hateren database⁷⁴, were multiplicatively scaled to have the same mean intensity as the background and had an average contrast of 45%.

For the mouse retina, we applied a similar procedure. In brief, the videos consisted of the same 325 images from the van Hateren database as used for the marmoset training stimulus, shown for 1 s each and jittered according to the horizontal gaze component²² of freely moving mice (graciously provided by A. Meyer; personal communication). We resampled the original 60 Hz gaze traces to produce a video with a refresh rate of 75 Hz. For our recordings, the one-dimensional gaze trajectory was randomly assigned to one of four orientations (0, 45, 90 or 135 degrees) for each 1 s image presentation. The amplitude of the original movement was transformed into micrometre on the retina using a retinal magnification factor of 31 μm deg^−1 for the mouse. All images were multiplicatively scaled to have the same mean intensity as the background. Test stimuli consisted of 30–35 cycles of 25 distinct natural images, paired with unique movement trajectories. The training stimuli consisted of batches of 35 images out of the remaining 300 (sampled with replacement), each paired with a unique movement trajectory.

For the model-based analyses of the responses to the natural videos, we applied a temporal binning corresponding to the stimulus update frequency (85 Hz for the marmoset and 75 Hz for the mouse) and used the spike count in each bin. To extract firing rates for the test stimuli, we averaged the binned responses over repeats. Furthermore, to eliminate cells with noisy responses, we only used cells for subsequent analyses with a symmetrized R² of at least 0.2 between even and odd trials of the test set.

All model predictions for natural videos used the stimulus training part for estimating an output nonlinearity and the test part for evaluation of model performance. For the LN model, we obtained the spatiotemporal stimulus filter (decomposed into a spatial and a temporal filter as explained in ‘Receptive-field characterization’) from the spatiotemporal white-noise experiments but estimated the nonlinearity from the natural-video data. To do so, we projected the video frames onto the upsampled spatial filter (to single-pixel resolution) and then convolved the result with the temporal filter. The output nonlinearity was obtained as a histogram (40 bins containing the same number of data points across the range of filtered video-stimulus signals) containing the average filtered signal and the average corresponding spike count. To apply the nonlinearity to the test data, we used linear interpolation of histogram values. We estimated model performance using the coefficient of determination between model prediction and measured firing rate to obtain the fraction of explained variance (R²). Negative values were clipped to zero.

We calculated video response correlations, using the trial-averaged firing rates of the test stimulus, as the Pearson correlation coefficient between the firing rates for each cell pair of the same type (as well as across specific types). We performed the same analyses for model predictions and for calculating correlations inherent to the test stimulus, where we calculated pairwise correlations of the light intensity of 5,000 randomly selected pixels. Decorrelation was defined for each cell pair as the difference between stimulus and response correlation relative to stimulus correlation for a pixel distance matching that of the actual cell pair distance. To generate correlation–distance curves (Fig. 1e), we sorted cell pairs by ascending distance and averaged pair correlations over groups of 20–60 pairs (depending on cell type, using fewer pairs per bin when the number of available cells was small).

Spike-train information and fractional redundancy

To estimate whether pairwise correlations led to coding redundancy, we quantified the information contained in ganglion cell spike trains by measuring entropies of response patterns in temporal-frequency space by evaluating the Fourier transforms of the response patterns^75,76. For temporal patterns that are sufficiently long compared to the time scales of correlations, this approach allows treating the different frequency modes independently and approximating, through the central limit theorem, the empirical distribution of Fourier components by normal distributions whose entropies can be analytically computed^75,76. This greatly reduces the sampling problem of information-theoretic evaluations encountered by direct methods of computing entropies through empirical frequencies of different response patterns⁷⁷.

Here we applied the method to spike-train responses (binned at 0.4 ms) from the repeated parts of the natural video (or white noise) and divided them into 0.8-s-long non-overlapping sections separately for each stimulus trial. This process yielded 27 (or 31) sections for the marmoset (or mouse) natural video and 20–22 sections for white noise for each trial (around 55 white-noise trials for marmoset and 40 for mouse recordings). The selection of the section length aimed at having comparable numbers of sections per trial and trials per section (both around 30) in the natural video analysis to mitigate bias effects from limited data in the calculation of information rates. For each section (s) and trial (t), we performed a Fourier transform to obtain complex-valued frequency coefficients that were then separated into real-valued cosine (c_cos) and sine (c_sin) coefficients for each frequency (f). For a single-cell analysis, we then estimated signal (H_signal) and noise (H_noise) entropies by computing the variance of those coefficients either over sections of a given trial or over trials for a given section, respectively, and then averaging the variances over the remaining dimension (that is, trials or sections, respectively):

where, for example, \({V}_{\sin }^{s}={\langle {{\rm{V}}{\rm{a}}{\rm{r}}({c}_{\sin }(f))}_{s}\rangle }_{t}\) denotes the variance of sine coefficients (subscript ‘sin’) over sections (superscript ‘s’), averaged over trials.

The frequency-resolved information rate was calculated as the difference of signal and noise entropies, normalized by the duration of the applied response sections to obtain information per time. The total information rate was then obtained as the sum over frequencies. For this sum, we applied an upper cutoff at 200 Hz, because signal and noise entropies had converged to the same baseline level by then.

For estimating the information content of a cell pair, we proceeded analogously, but instead of computing the variances of the sine and cosine coefficients directly, we first gathered the sine and cosine coefficients from both cells to compile the corresponding 4 × 4 covariance matrix over sections (or trials) and averaged the covariance matrices over trials (or sections). We then used the four eigenvalues (\({\lambda }_{k}\)) of each averaged covariance matrix to calculate the response entropy for a cell pair (separately for signal and noise):

Information rates were again obtained as the difference between signal and noise entropy, summed over frequencies and normalized by the duration of the response sections. To check for bias from finite data in the calculation of information rates⁷⁸, we also computed information rates for different fractions of the full dataset but observed little systematic dependence on the size of the data fraction. This is for two reasons. First, the possibility to obtain entropies analytically only after estimating the variances of the Fourier components greatly limits the sampling problem, and second, the comparable numbers of trials and sections used in the estimation of entropies mean that any residual bias is of similar scale for signal and noise entropies, thus leading to at least partial cancellation.

To obtain the contributions of individual frequency bands to the information rates, we used the same approach as above separately for each frequency component without summation over frequencies.

Fractional redundancy for a cell pair (i, j) was calculated on the basis of a previous definition^12,19 as the difference between the sum of single-cell information values (I_i and I_j) and pair information (I_ij) normalized by the minimum single-cell information:

Other definitions of redundancy, in particular in the context of efficient coding, are based on a comparison of the actual information passed through an information channel (here corresponding to the joint responses of the cell pair and their information rate I_ij) and the channel capacity: that is, the maximum information that the channel could supply^2,79. In practice, however, channel capacity is difficult to assess and requires fundamental assumptions about the neural code and attainable firing rates. Instead, the comparison of I_ij to the sum of single-cell information rates, as used here, can be thought of as capturing whether the capacity as specified by the constraints of the individual cells’ response characteristics is fully exhausted by the joint responses. Thus, fractional redundancy is sensitive to inefficient use of the channel capacity that stems from correlation but not from inefficient coding by individual cells.

Analysis of fixations and spatial contrast

To investigate the effects of spatial contrast on response correlations, we divided the test part (repeated image sequences) of the natural video into distinct fixations by detecting saccadic transitions. To do so, we first marked each time point when a new image was presented as a transition. In each image presentation, we calculated the distance between consecutive positions to estimate the instantaneous eye velocity and used MATLAB’s ‘findpeaks’ function to obtain high-velocity transitions. We constrained peak finding for the marmoset (and mouse) to a minimum peak time interval of 47 (and 53) ms and a minimum amplitude of 10 (and 300) deg s^−1. This process yielded 80 fixations for the marmoset and 68 fixations for the mouse video. Fano factors were computed for individual fixations. To reduce effects of nonstationary activity, we included here only cells with a positive symmetrized coefficient of determination between the firing-rate profiles of the first half and second half of trials. To mitigate noise from fixations with no or little activity, we excluded, for each cell, fixations with fewer than three spikes on average and report the average Fano factor over fixations, weighted by the mean spike count.

For each video frame and each ganglion cell, spatial contrast was calculated as described previously³⁶ using the standard deviation of pixels inside the cell’s receptive field, weighted by the receptive-field profile. For each fixation, we assigned to each cell the median spatial contrast of all frames during the fixation period. We also assigned a linear activation per fixation, estimated by filtering video frames with the spatial filter obtained from white noise and taking the median over all fixation frames.

To reduce effects of the light level on the analysis of spatial contrast, we aimed at separating the fixations into high-spatial-contrast and low-spatial-contrast groups while balancing the linear activation between the groups. For a pair of cells, we therefore sorted all fixations of the test set by the average linear activation across both cells and paired neighbouring fixations in this sorted list. This led to 40 pairs (34 for the mouse), and for each pair, we assigned the fixation with the higher spatial contrast to the high-spatial-contrast group and the other fixation to the low-spatial-contrast group. To expand the pairwise correlation (r_pair) into high- and low-spatial-contrast parts, we split the numerator of the Pearson correlation coefficient so that r_pair = r_high + r_low, with

with x and y corresponding to the responses of the two cells and i indexing the frames of the natural video, the sum here running over the frames from high-spatial-contrast fixations and N_frames denoting the total number of frames. Mean (\(\bar{x}\), \(\bar{y}\)) and standard deviation (\({\sigma }_{X}\), \({\sigma }_{Y}\)) values correspond to the length of the entire test part of the video.

Extraction of DS ganglion cells

To identify DS ganglion cells in the mouse retina, we used drifting sinusoidal gratings of 100% contrast, 240 μm spatial period and a temporal frequency of 0.6 Hz, moving along eight different, equally spaced directions. We analysed cell responses as previously described³⁶. Cells with a mean firing rate of at least 1 Hz and a direction selectivity index (DSI) of at least 0.2 (significant at 1% level) were considered putative DS cells. The DSI was defined as the magnitude of the normalized complex sum \(\sum _{\theta }{r}_{\theta }{e}^{i\theta }\,/\sum _{\theta }{r}_{\theta }\), with θ specifying the drift direction and r_θ the average (across trials) spike count during the grating presentation for direction θ (excluding the first grating period). The preferred direction was obtained as the argument of the same sum. The statistical significance of the DSI was determined through a Monte Carlo permutation approach^28,36.

To separate ON from ON–OFF DS cells, we used a moving-bar stimulus. The bar (width: 300 μm, length: 1,005 μm) had 100% contrast and was moved parallel to the bar orientation in eight different directions with a speed of 1,125 μm s^−1. We extracted a response profile to all bar directions through singular value decomposition, as previously described²⁴ and calculated an ON–OFF index to determine whether cells responded only to the bar onset (ON) or to both onset and offset (ON–OFF). Cells with an ON–OFF index (computed as the difference of onset and offset spike-count responses divided by their sum) above 0.4 were assigned as ON DS cells and were grouped into three clusters on the basis of their preferred directions.

Flashed gratings

Depending on the experiment, we generated 1,200 to 2,400 different sinusoidal gratings with 25 or 30 different spatial frequencies (f), with half-periods between 15 and 1,200 μm, roughly logarithmically spaced. For each grating, we generated 12 or 10 equally spaced orientations (θ) and four or eight equally spaced spatial phases (\(\varphi \)). For a given grating, the contrast value for each pixel with (x, y) coordinates were generated according to the following equation:

Gratings were presented as 200 ms flashes on the retina, separated by a 600 or 800 ms grey screen. The order of presentation was pseudorandom. We collected spike-count responses to the flashes by counting spikes during stimulus presentation for the marmoset or 20 ms after stimulus onset up to 20 ms after stimulus offset for the mouse. We used tuning surfaces to summarize responses (Extended Data Fig. 6), which we generated by averaging responses over trials and spatial phases for each frequency–orientation pair. In the mouse recordings, in which we typically collected four to five trials per grating, we calculated symmetrized R² values for the spike counts, and we only used cells with an R² of at least 0.2 for further analyses. In marmoset recordings, we typically collected one to two trials per grating, and we thus used no exclusion criterion.

DoG subunits

The subunit grid model consists of DoG subunits, and fitting its parameters to data is facilitated by an analytical solution of the DoG activation by a grating. The latter was obtained by considering the grating activations of both centre and surround elliptical Gaussians on the basis of previous calculations⁸⁰, as described in the following. The DoG receptive field was defined with these parameters: standard deviations \({\sigma }_{x}\) and \({\sigma }_{y}\) at the x and y axis, the orientation of the x axis θ_DoG, the spatial scaling for the subunit surround k_s and a factor determining the relative strength of the surround w_s. Concretely, the response of a DoG receptive field (r_DoG) centred at (x_o, y_o) to a parametric sinusoidal grating (\(f,\theta ,\varphi \)) is

with the amplitude A_DoG given by

with

The receptive-field phase \({\Theta }_{{\rm{DoG}}}\) is given by

DoG LN model

We fitted parameterized DoG LN models to the measured grating responses. The full model combined the DoG receptive-field activation with an output nonlinearity, for which we chose a logistic function \(N(x)={(1+{e}^{-x})}^{-1}\). The model response (R), denoting the modelled neuron’s firing rate, was thus given by

where \({\beta }_{{\rm{DoG}}}\) and \({\gamma }_{{\rm{DoG}}}\) are parameters determining the steepness and threshold of the output nonlinearity and \(a\) is a response scaling factor.

All model parameters (\({x}_{{\rm{o}}},{y}_{{\rm{o}}},{\sigma }_{x},{\sigma }_{y},{\theta }_{{\rm{DoG}}},{k}_{{\rm{s}}},{w}_{{\rm{s}}},\,{{\beta }_{{\rm{DoG}}},\gamma }_{{\rm{DoG}}},a\)) were optimized simultaneously by minimizing the negative Poisson log-likelihood, using constrained gradient descent in MATLAB with the following constraints: \({\sigma }_{x},{\sigma }_{y} > 7.5\,{\rm{\mu }}{\rm{m}},\,-{\rm{\pi }}/4 < {\theta }_{{\rm{DoG}}} < {\rm{\pi }}/4,\) \(1 < {k}_{s} < 6,a > 0\). Each trial was used independently for fitting.

Subunit grid model

We fitted all subunit grid models with 1,200 potential subunit locations, placed on a hexagonal grid around a given receptive-field centre location. The centre was taken as the centre of a fitted DoG model. The subunits were spaced 16 μm apart. Each subunit had a circular DoG profile with a standard deviation of \(\sigma \) (centre Gaussian) and centred at (\({x}_{{\rm{os}}},{y}_{{\rm{os}}}\)), and its activation in response to a grating was given by

where both amplitude and phase are given by the DoG receptive-field formulas with \({\sigma }_{x}={\sigma }_{y}=\sigma \).

The full response model was

where \(N(x)={(1+{e}^{-x})}^{-1}\) is a logistic function, \(\beta \) and \(\gamma \) are parameters determining the steepness and threshold of the subunit nonlinearity, N_sub is the number of subunits with non-zero weights, \({w}_{{\rm{s}}}\) are positive subunit weights, and \(G\) is a Naka–Rushton output nonlinearity \(G(x)=a{x}^{n}/({x}^{n}+{k}^{n})+b\), with non-negative parameters \({{\rm{\theta }}}_{{\bf{out}}}=(a,b,n,k)\).

Fitting and model selection

We optimized subunit grid models using the stochastic optimization method ADAM⁸¹ with the following parameters: batch size = 64, β₁ = 0.9, β₂ = 0.999, ε = 10^−6. For the learning rate (η), we used a schedule with a Gaussian profile of μ = N_epochs/2 and σ = N_epochs/5: this led to a learning rate that was low in the beginning of the training, peaked midway and was lowered again towards the end. Peak learning rate was set to η_max = 0.005. The number of epochs (N_epochs) was fixed for all cells to 4 × 10⁵/N_trials, with N_trials representing the number of all grating presentations used for fitting, which typically resulted in 50–150 epochs.

To enforce parameter constraints during fitting, such as non-negativity, we used projected gradient descent. We also aimed at regularizing the parameter search in a way that non-zero subunit weights were penalized more strongly when other subunits with non-zero weights were spatially close. We therefore introduced a density-based regularizer that controlled the coverage of the receptive field with a flexible number of subunits (Extended Data Fig. 6).

Concretely, the cost function we minimized was

with N_sp being the total number of spikes, L the Poisson likelihood, s_G the vector of all grating parameters used, r_G the corresponding spike-count response vector, \({{\rm{\theta }}}_{{\bf{p}}}\) = (\(\sigma ,{k}_{s},{w}_{s},\,\beta ,\,\gamma ,\,{{\rm{\theta }}}_{{\bf{out}}}\)) all the shared model parameters, and \({\bf{w}}=({w}_{1},\,\ldots ,\,{w}_{{N}_{{\rm{sub}}}})\) the vector containing all subunit weights. \(\lambda \) controls the regularization strength, which depends on the pairwise subunit distances d_si.

After the end of the optimization, we pruned subunit weights with small contributions or weights that ended up outside the receptive field. To do so, we first set to zero every weight smaller than 5% of the maximum subunit weight. We then fitted a two-dimensional Gaussian to an estimate of the receptive field, obtained by summing subunit receptive fields weighted by the subunit weights. The weight corresponding to any subunit centre lying more than 2.5σ outside that Gaussian was set to zero. To ensure proper scaling of the output nonlinearity after weight pruning, we refitted the output nonlinearity parameters along with a global scaling factor for the weights.

We typically fitted six models per cell with different regularization strengths \(\lambda \) ranging from 10^−6 to 5 × 10^−4. To select for the appropriate amount of regularization, we only accepted models that yielded at least three subunits and had a low receptive-field coverage (less than 3; see below). If no eligible model was fitted, cells were excluded from further analyses. Among the remaining models, we selected the one that minimized the Bayesian information criterion, which we defined for the subunit grid model as

where N_sub is again the number of subunits with non-zero weights, N_data is the number of grating-response pairs used to fit the model and L the likelihood of the fitted model. The selected model balanced good prediction performance and realistic receptive-field substructure. Note, though, that the actual size and layout of the subunits might not be critical to obtain good model performance³¹ as long as appropriate spatial nonlinearities are included, and that the subunit nonlinearities are generally better constrained by the data than the subunits themselves (Extended Data Fig. 6).

Parameter characterization of the subunit grid model

To summarize how densely subunits covered a cell’s receptive field, we defined a measure for the subunit coverage. It was calculated as the ratio A/B, where A was the subunit diameter (4σ of the centre Gaussian) and B was the average distance between subunit centre points. For a particular cell, the average subunit distance was calculated as the average over all nearest-neighbour distances, weighted by each pair’s average subunit weight. If fewer than three subunits had non-zero weights in the model, no coverage value was computed.

To plot and characterize subunit nonlinearities, we first added an offset so that an input of zero corresponded to zero output. We then scaled the nonlinearities so that the maximum value over the input range [−1, 1] was unity. Following offsetting and scaling, we calculated nonlinearity asymmetries to quantify the response linearity of subunits as (1 − M)/(1 + M), where M is the absolute value of the minimum of the nonlinearity over the input range \([-1,\,1]\).

Natural images and response predictions

We flashed a series of 220 (or 120) natural images to the retina, as described previously³⁶. We used images from the van Hateren database, which were cropped to their central 512 × 512 pixel square and presented over the multielectrode array at single-pixel resolution. All images were multiplicatively scaled to have the same mean intensity as the background. Interspersed with the natural images, we also presented artificial images. The images were generated as black-and-white random patterns at a single-pixel level and then blurred with Gaussians of eight different spatial scales²⁹, but the corresponding responses were not analysed as part of this study. All images were flashed for 200 ms, separated by either 600 or 800 ms of grey background illumination. Images were flashed in a randomized order, and we typically collected eight trials per image. Average spike counts were calculated in the same way as in the case of flashed gratings, and only cells with symmetrized R² of at least 0.2 were used for further analyses.

To calculate response predictions for models built with white noise, we used the output of spatial filters applied to the natural images. The filters were upsampled to match the resolution of the presented images and normalized by the sum of their absolute values. For models obtained from responses to flashed gratings, DoG receptive fields were instantiated at single-pixel resolution, and the natural images were then projected onto the DoG receptive fields. For the subunit model, the subunit filter outputs were passed through the fitted subunit nonlinearity and then summed while applying the subunit weights. The performance for each model was calculated as the Spearman rank correlation ρ between the model output (without an explicit output nonlinearity) and cell responses to the natural images²⁸.

Flickering gratings and spatiotemporal DoG LN models

We generated 3,000 (or 4,800) different gratings with 25 (or 30) different spatial frequencies, between 7.5 and 1,200 μm half-periods, roughly logarithmically spaced. For each grating, we generated 20 orientations and six (or eight) spatial phases. The gratings were presented in pseudorandom sequence, updated at a 85 (or 75) Hz refresh rate. Every 6,120 (or 3,600) frames, we interleaved a unique sequence of 1,530 (or 1,200) frames that was repeated throughout the recording to evaluate response quality.

We fitted a spatiotemporal DoG LN model to the grating responses. The temporal filters spanned a duration of 500 ms and were modelled as a linear combination of ten basis functions. The response delay was accounted for with two square basis functions for each of the two frames before a spike. The remaining eight were chosen from a raised cosine basis, with peaks ranging from 0 to 250 ms before a spike.

Concretely, the spatiotemporal DoG model had the form

where \(N(x)={(1+{e}^{-x})}^{-1}\) is a logistic function, k_Ct and k_St are separate temporal filters for the centre and the surround, b determines the baseline activation, and \(a\) is a response scaling factor. The vectors r_C and r_S contain DoG receptive-field activations for 500 ms before a particular frame and were calculated as for the flashed gratings. The model was fitted with nonlinear constrained optimization, with DoG constraints identical to the case of flashed gratings and \(a > 0\).

Spatiotemporal subunit grid model

We also fitted a spatiotemporal subunit grid model to the grating responses. Our strategy was similar to the case of flashed gratings. We fitted each subunit grid model with 1,200 subunit locations, placed in a hexagonal grid around a given receptive-field centre location. The centre was taken as the fitted centre of the DoG model. The subunits were spaced 16 μm apart. The model response (R) was given by

where \({w}_{s}\) are non-negative subunit weights, \(N(x)\) is a logistic function, k_Ct and k_St are separate temporal filters for the centre and the surround shared across all subunits, and \(\gamma \) determines the nonlinearity threshold. We used a Naka–Rushton output nonlinearity \(G(x)=a{x}^{n}/({x}^{n}+{k}^{n})\), with non-negative parameters \({{\rm{\theta }}}_{{\bf{out}}}=(a,n,k)\). The vectors r_c (r_s) contain Gaussian centre (surround) subunit activations for 500 ms before a particular frame and for each subunit. The parameters required to fit DoG subunits are the standard deviation of the centre, the scaling for the subunit surround and a factor determining the relative strength of the surround.

We used stochastic gradient descent with the ADAM optimizer to fit spatiotemporal models. The parameters were the same as in the flashed-grating models, except for the batch size = 2,000 and η_max = 0.02. We used the same learning schedule for η and the same regularization to control for subunit density as in the case of flashed gratings.

Natural video predictions of grating-fitted models

To obtain natural video predictions for models built from flickering gratings, we instantiated receptive fields, as well as subunit filters, at single-pixel resolution. Again, we projected video frames on centre and surround filters separately, convolved each result with the corresponding temporal filter and summed the two outputs for obtaining the final filter output. For subunit grid models, the subunit nonlinearity fitted from the gratings was applied to the linear subunit outputs, which were then summed with the non-negative weights to obtain the final activation signal. The training part of the video was used for estimating an output nonlinearity using maximum likelihood (under Poisson spiking) for both the DoG LN and the subunit grid models. The nonlinearity had the same parametric form as in the model fit with gratings. Unlike the models applied to natural images, in which the Bayesian information criterion was applied, we here used the training set to select the appropriate regularization strength by finding the maximum of the log-likelihood among the eligible models (with at least three subunits and a receptive-field coverage below 3). If no eligible model was fitted, cells were excluded from further analyses. Model performance was estimated for the test set using the coefficient of determination between model prediction and measured firing rate as a fraction of explained variance (R²). Negative values of R² were clipped to zero.

To better differentiate DoG and subunit grid model performance, we selected fixations on the basis of model predictions. For each cell pair, we selected the 20% of the fixations for which the deviation in the predictions of the two models, averaged over the two cells, was largest. For a single cell and a single fixation, the deviations were calculated as the absolute value of model differences normalized by the cell’s overall response range (maximum minus minimum during the test part of the video) and averaged over all frames of the fixation. Performance of both models (R²) was then compared to the frame-by-frame neural response on these fixations and averaged over the two cells. The selection of maximally differentiating fixations does not favour either model a priori, because it is only based on how much model predictions differ and not on their performance in explaining the data.

Similar to the spatial contrast analysis, we expanded the pairwise correlation (r_pair) into linear and nonlinear contributions by splitting the numerator of the Pearson correlation coefficient so that r_pair = r_nonlinear + r_linear. For a pair of cells, we sorted all fixations (in descending order) by the average deviation of model predictions. We assigned the first half of the fixations to the nonlinear group and the remaining ones to the linear group.

Reporting summary

Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.