Local involvement and ethics
We worked closely with the local population of Copan, sought approval and feedback from officials at the Ministry of Health (MOH) of Honduras, and endeavoured to provide practical benefits to the local community. When we began designing the underlying cohort project in 2013 (in 176 villages, including the 18 used here), the Bill and Melinda Gates Foundation introduced us to the Inter-American Development Bank (IDB), which has been supporting and doing work throughout Latin America, and the IDB in turn introduced us to the MOH. Because of this pathway to getting the project launched, we worked with local and regional public health agencies and with local leaders rather than with academic partners.
The area we chose to work in the western highlands of Honduras, Copan, is very isolated. Over the years, as we built our data collection team in Copan, we developed deep ties to the local community, to local village leaders and to the few local health clinics there, as well as to local transportation and infrastructure providers. Because of these ties and our commitment to the local community, we presented our results directly to these constituencies regularly at the completion of our various projects.
We provided other material benefits to the local community, beyond simply providing them with information. When we tested people for stool parasites, we gave them the results of their tests and arranged for them to be treated. When we tested people for vision, we provided corrective glasses. We solicited ideas from the local community about what infrastructure improvements we could make, and we repaired many local playgrounds and clinics as a result. We arranged for an American company to provide free portable handheld ultrasound devices to the local health clinics, which was much appreciated by local providers. In terms of capacity building, we hired and trained over 100 local people, and many of our former data collectors have gone on to work for other public health and development entities. Finally, we offered a talented young person from Copan a position as a PhD student in the USA.
Throughout our work in Honduras, along with our extensive involvement at local and national levels, we have endeavoured to act with integrity, curiosity and respect in all our relationships.
This research would not have been prohibited in the USA. This work is not likely to result in stigmatization, incrimination or discrimination or personal risk for the participants, and we have safeguarded all data from threats to the privacy or security of our participants.
All participants provided informed consent, and our work was approved by the Yale Committee on Human Subjects (reference no. 2000020688).
Network construction
Village-level networks were mapped with standard âname generatorsâ for the whole village. After a photographic census (of all adolescent and adult residents) was taken for each village, we conducted the main network survey in each village, including a detailed, hour-long survey7, incorporating demographic and health measures, as well as a battery of name generators with which respondents identified relevant social relationships (friends, family members, people they spend free time with, and so on) through names and photographs shown in our TRELLIS software (available at trellis.yale.edu)45. All the name generator questions are listed in Supplementary Table 1.
For questions in which a pair reported different levels of the same variable, such as greeting type or the amount of free time, we symmetrized the variables as follows: for greeting type, we reported the greeting type involving the most physical contact. For the frequency of free time and shared meals between a pair, we symmetrized by choosing the response that indicates more frequent contact. We symmetrized all other responses at the relationship level here (that is, when either of two people nominate each other as a âclose friendâ, we counted it). When calculating degree distributions, centralities and clustering, we simplified our networks to remove multiplexity (that is, we concatenated all ties between pairs of people) and symmetrized the ties (that is, we ignored who nominated whom in each pair).
Social network graphs were analysed and geodesic distances and centrality measures were calculated with igraph (v.1.3.5)46 and plotted with the FruchtermanâReingold algorithm. To protect the anonymity of our study villages, the villages were renamed to random town names from another country.
Sample collection and sequencing
Participants were instructed on how to self-collect the faecal samples using a training module delivered in person in the villages and were asked to return samples promptly to the local team. Samples were refrigerated immediately upon collection and then stored in liquid nitrogen at the collection site within 12âh after collection and moved to a â80â°C freezer in Copan Ruinas, Honduras. All the villages followed the same procedures. Samples were shipped, in randomized allotments, on dry ice to the USA and stored in â80â°C freezers.
Stool material was homogenized using TissueLyzer from Qiagen, and the lysate was prepared for extraction with the Chemagic Stool gDNA extraction kit (Perkin Elmer) and extracted on the Chemagic 360 Instrument (Perkin Elmer) following the manufacturerâs protocol. Sequencing libraries were prepared using the KAPA Hyper Library Preparation kit (KAPA Biosystems). Shotgun metagenomic sequencing was carried out on Illumina NovaSeq 6000. Samples not reaching the desired sequencing depth of 50âGbp were resequenced on a separate run. Raw metagenomic reads were deduplicated using prinseq lite47 (v.0.20.2) with default parameters. The resulting reads were screened for human contamination (hg19) with BMTagger and then quality filtered with Trimmomatic48 (v.0.36, parameters âILLUMINACLIP: nextera_truseq_adapters.fasta:2:30:10:8:true SLIDINGWINDOW: 4:15 LEADING: 3 TRAILING: 3 MINLEN: 50â). This resulted in a total of 1,787 samples (with an average size of 8.6âÃâ107 reads).
Species-level and strain-level profiling
Species-level profiling was performed using MetaPhlAnâ426 using the Jan21 database and default parameters. Strain-level profiling was performed for a subset of species present in at least 50 samples using StrainPhlAnâ426 with parameters â–marker_in_n_samples 1 –sample_with_n_markers 10 — phylophlan_mode accurateâ. This resulted in a total of 841 species-level genome bins (SGB) and 339,137 profiled strains. The StrainPhlAn âstrain_transmission.pyâ script was used to assess transmission events using the produced trees, which yielded a total of 513,177 identified events. For a robust calculation, strain-sharing rates were calculated only for pairs sharing at least ten SGBs.
Beta diversity indices were calculated using the vegdist function from the vegan R package (v.2.6-2)49.
Separation of distances by village membership was tested by permutational multivariate analysis of variance (PERMANOVA) using the adonis function from the vegan R package with 999 permutations.
Statistical analyses
All statistical analyses were performed in R (v.4.1.3). Correction for multiple testing (BenjaminiâHochberg procedure, marked Padj) was applied when appropriate, and significance was defined at Padj<â0.05. All tests were two-sided except where otherwise specified. All egocentric regressions (that is, when we assess the relationship of network position and strain-sharing) involved linear mixed-effects models with this general formula specification:
$$\begin{array}{c}{\rm{O}}{\rm{u}}{\rm{t}}{\rm{c}}{\rm{o}}{\rm{m}}{\rm{e}}\,{\rm{o}}{\rm{f}}\,{\rm{i}}{\rm{n}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{e}}{\rm{s}}{\rm{t}} \sim {\rm{p}}{\rm{r}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{c}}{\rm{t}}{\rm{o}}{\rm{r}}\,{\rm{o}}{\rm{f}}\,{\rm{i}}{\rm{n}}{\rm{t}}{\rm{e}}{\rm{r}}{\rm{e}}{\rm{s}}{\rm{t}}+{\rm{a}}{\rm{g}}{\rm{e}}+{\rm{s}}{\rm{e}}{\rm{x}}\\ \,+\,{\rm{B}}{\rm{M}}{\rm{I}}+{\rm{B}}{\rm{r}}{\rm{i}}{\rm{s}}{\rm{t}}{\rm{o}}{\rm{l}}\,{\rm{s}}{\rm{t}}{\rm{o}}{\rm{o}}{\rm{l}}\,{\rm{s}}{\rm{c}}{\rm{a}}{\rm{l}}{\rm{e}}+{\rm{h}}{\rm{o}}{\rm{u}}{\rm{s}}{\rm{e}}{\rm{h}}{\rm{o}}{\rm{l}}{\rm{d}}\,{\rm{w}}{\rm{e}}{\rm{a}}{\rm{l}}{\rm{t}}{\rm{h}}\,{\rm{i}}{\rm{n}}{\rm{d}}{\rm{e}}{\rm{x}}\\ \,+\,{\rm{d}}{\rm{i}}{\rm{e}}{\rm{t}}\,{\rm{d}}{\rm{i}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{s}}{\rm{i}}{\rm{t}}{\rm{y}}\,{\rm{s}}{\rm{c}}{\rm{o}}{\rm{r}}{\rm{e}}+{\rm{m}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{c}}{\rm{a}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}\,{\rm{u}}{\rm{s}}{\rm{a}}{\rm{g}}{\rm{e}}+{\rm{w}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}\,{\rm{s}}{\rm{o}}{\rm{u}}{\rm{r}}{\rm{c}}{\rm{e}}\\ \,+\,{\rm{D}}{\rm{N}}{\rm{A}}\,{\rm{c}}{\rm{o}}{\rm{n}}{\rm{c}}{\rm{e}}{\rm{n}}{\rm{t}}{\rm{r}}{\rm{a}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}+{\rm{s}}{\rm{e}}{\rm{q}}{\rm{u}}{\rm{e}}{\rm{n}}{\rm{c}}{\rm{i}}{\rm{n}}{\rm{g}}\,{\rm{d}}{\rm{e}}{\rm{p}}{\rm{t}}{\rm{h}}+{\rm{e}}{\rm{x}}{\rm{t}}{\rm{r}}{\rm{a}}{\rm{c}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}\,{\rm{d}}{\rm{a}}{\rm{t}}{\rm{e}}\\ \,+\,{\rm{s}}{\rm{h}}{\rm{i}}{\rm{p}}{\rm{p}}{\rm{i}}{\rm{n}}{\rm{g}}\,{\rm{b}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}+{\rm{s}}{\rm{e}}{\rm{q}}{\rm{u}}{\rm{e}}{\rm{n}}{\rm{c}}{\rm{i}}{\rm{n}}{\rm{g}}\,{\rm{b}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}+{\rm{e}}{\rm{x}}{\rm{t}}{\rm{r}}{\rm{a}}{\rm{c}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}\,{\rm{b}}{\rm{a}}{\rm{t}}{\rm{c}}{\rm{h}}\\ \,+\,(1|{\rm{v}}{\rm{i}}{\rm{l}}{\rm{l}}{\rm{a}}{\rm{g}}{\rm{e}})+(1|{\rm{b}}{\rm{u}}{\rm{i}}{\rm{l}}{\rm{d}}{\rm{i}}{\rm{n}}{\rm{g}})\end{array}$$
That is, we controlled for age, sex, wealth, Bristol stool scale and body mass index (BMI), as well as sample properties (for example, DNA concentration) and village fixed effects. We also included household water source, individual medication usage in the last month and diet diversity (the number of food categories consumed on a daily basis10). Medication types included: painkillers, antibiotics, anti-diarrhoeal, anti-parasitic, anti-fungal, anti-diabetics, antacids, laxatives and vitamins. Mixed-effects models were created with the lmertest package (v.3.1.3)50.
Network predictions
Mixed-effects logistic regression models were used for out-of-sample network predictions. Class-balanced data sets were constructed by down-sampling the number of unrelated pairs to equal the number of related pairs, and we trained our model using k-fold cross-validation with kâ=â3, and predictions from the three separate test sets were combined. ROC curves were constructed from the average of five sets of threefold cross-validation. ROC curves and confidence intervals were calculated with the pROC package (v.1.18.0)51 and logistic regression models were constructed with the lmertest package (v.3.1.3) with the binomial family link function and a random slope per village.
The predictive model including all covariates was specified by the following formula:
$$\begin{array}{c}{\rm{R}}{\rm{e}}{\rm{l}}{\rm{a}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}{\rm{s}}{\rm{h}}{\rm{i}}{\rm{p}} \sim {\rm{m}}{\rm{i}}{\rm{c}}{\rm{r}}{\rm{o}}{\rm{b}}{\rm{i}}{\rm{o}}{\rm{m}}{\rm{e}}\,{\rm{s}}{\rm{i}}{\rm{m}}{\rm{i}}{\rm{l}}{\rm{a}}{\rm{r}}{\rm{i}}{\rm{t}}{\rm{y}}+{\rm{s}}{\rm{e}}{\rm{x}}\\ \,+\,{\rm{i}}{\rm{n}}{\rm{d}}{\rm{i}}{\rm{g}}{\rm{e}}{\rm{n}}{\rm{o}}{\rm{u}}{\rm{s}}\,{\rm{s}}{\rm{t}}{\rm{a}}{\rm{t}}{\rm{u}}{\rm{s}}+{\rm{r}}{\rm{e}}{\rm{l}}{\rm{i}}{\rm{g}}{\rm{i}}{\rm{o}}{\rm{n}}+{\rm{a}}{\rm{g}}{\rm{e}}\,{\rm{d}}{\rm{i}}{\rm{f}}{\rm{f}}{\rm{e}}{\rm{r}}{\rm{e}}{\rm{n}}{\rm{c}}{\rm{e}}\\ \,+\,{\rm{a}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{a}}{\rm{g}}{\rm{e}}\,{\rm{a}}{\rm{g}}{\rm{e}}+{\rm{w}}{\rm{e}}{\rm{a}}{\rm{l}}{\rm{t}}{\rm{h}}\,{\rm{d}}{\rm{i}}{\rm{f}}{\rm{f}}{\rm{e}}{\rm{r}}{\rm{e}}{\rm{n}}{\rm{c}}{\rm{e}}+{\rm{a}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{a}}{\rm{g}}{\rm{e}}\,{\rm{w}}{\rm{e}}{\rm{a}}{\rm{l}}{\rm{t}}{\rm{h}}\\ \,+\,{\rm{e}}{\rm{d}}{\rm{u}}{\rm{c}}{\rm{a}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}\,{\rm{d}}{\rm{i}}{\rm{f}}{\rm{f}}{\rm{e}}{\rm{r}}{\rm{e}}{\rm{n}}{\rm{c}}{\rm{e}}+{\rm{a}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{a}}{\rm{g}}{\rm{e}}\,{\rm{e}}{\rm{d}}{\rm{u}}{\rm{c}}{\rm{a}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}\\ \,+\,{\rm{m}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{c}}{\rm{a}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}\,{\rm{u}}{\rm{s}}{\rm{a}}{\rm{g}}{\rm{e}}+{\rm{s}}{\rm{a}}{\rm{m}}{\rm{e}}\,{\rm{w}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}\,{\rm{s}}{\rm{o}}{\rm{u}}{\rm{r}}{\rm{c}}{\rm{e}}+{\rm{d}}{\rm{i}}{\rm{e}}{\rm{t}}\\ \,+\,{\rm{B}}{\rm{r}}{\rm{i}}{\rm{s}}{\rm{t}}{\rm{o}}{\rm{l}}\,{\rm{s}}{\rm{t}}{\rm{o}}{\rm{o}}{\rm{l}}\,{\rm{s}}{\rm{c}}{\rm{a}}{\rm{l}}{\rm{e}}+{\rm{h}}{\rm{o}}{\rm{u}}{\rm{s}}{\rm{e}}{\rm{h}}{\rm{o}}{\rm{l}}{\rm{d}}\,{\rm{s}}{\rm{h}}{\rm{a}}{\rm{r}}{\rm{i}}{\rm{n}}{\rm{g}}\\ \,+\,(0+{\rm{m}}{\rm{i}}{\rm{c}}{\rm{r}}{\rm{o}}{\rm{b}}{\rm{i}}{\rm{o}}{\rm{m}}{\rm{e}}\,{\rm{s}}{\rm{i}}{\rm{m}}{\rm{i}}{\rm{l}}{\rm{a}}{\rm{r}}{\rm{i}}{\rm{t}}{\rm{y}}|{\rm{v}}{\rm{i}}{\rm{l}}{\rm{l}}{\rm{a}}{\rm{g}}{\rm{e}}\,{\rm{I}}{\rm{D}})\end{array}$$
where âmicrobiome similarityâ is either the strain-sharing rate, Jaccard index or BrayâCurtis dissimilarity calculated between the members of a pair.
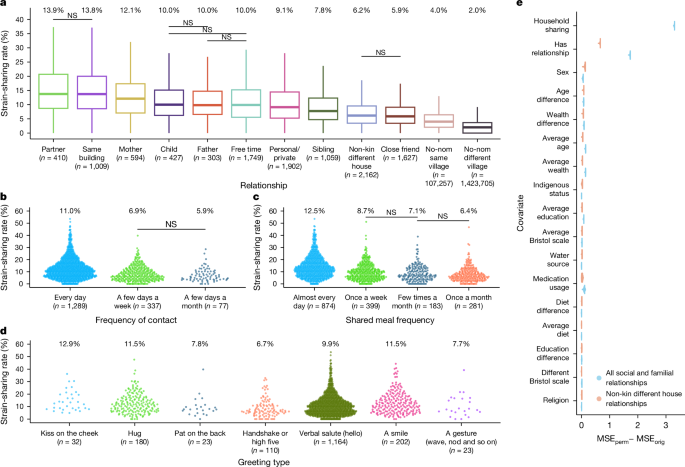
Variable importance metrics were calculated based on the permutation feature importance metric using the car R package (v.3.0). The permutation feature importance is defined to be the decrease in a model score when a single feature value is shuffled randomly52. This procedure breaks the relationship between the feature and the target; thus, the drop in the model score is indicative of how much the model depends on the feature. Variable importance metrics were analysed after 1,000 random permutations of each feature. Variable inflation factor values were calculated to ensure the reliability of results against collinearity of variables and were all low (less than 2).
Microbiome null permutations
Microbiome null permutations create a null distribution of strain-sharing rates between any two people while accounting for (just) the network structure. Under the null hypothesis that a hostâs microbiome composition and social network are independent, we can sever their relationship by randomly permuting the microbiome of every person in the village and recalculating metrics of interest, for example, strain-sharing by degree or clustering Rand indices. This ensures that the inherent structural pattern of the network remains the same, but the node values are randomized. This allows us to observe the distribution of our statistics if the human microbiome is fostered independently of any host social interactions.
Village-wide microbiome permutations were used to calculate null distributions for the strain-sharing rate by geodesic distance and for the clustering results. For relationship-specific permutations in Supplementary Fig. 1, permutations at the relationship level were taken instead of full village permutations. The observed distribution of relationship-specific sharing was compared with the distribution of sharing observed when that specific relationship tie was permuted, for example, comparing the sharing between someone and their friend versus someone and 100 random peopleâs friends in the same village. For the inherently gendered relationships of husband/wife and mother/father of a child, we accounted for the sex of the ego, but for all other relationships that are not necessarily gendered (for example, free time), we did not.
Longitudinal analyses
A subset of 301 people from four villages were followed-up after a period of 2âyears and asked to provide a second stool sample. Samples were processed consistently with the same pipeline used to analyse the previously processed 1,787 samples.
We defined relationship ties by using the same social network from the initial wave and evaluated the following linear mixed-effect model formula:
$${\rm{SS}}{{\rm{R}}}_{{\rm{T}}2} \sim SS{R}_{{\rm{T}}1}+{\rm{relationship}}+M+(1| {\rm{village}}\,{\rm{ID}})+(1| {\rm{ego}})$$
where SSRT1 and SSRT2 are the strain-sharing rate in pairs of people at time points T1 and T2, respectively. We show standardized coefficients.
To decompose the effect of sharing across all species, we used a mixed-effect logistic model formula specified as follows:
$${\rm{T}}{2}_{S} \sim {\rm{T}}{1}_{S}+{\rm{relationship}}+M+(1| {\rm{species}})+(1| {\rm{villageID}})+(1| {\rm{ego}})$$
where \({\rm{T}}{1}_{S}\) and \({\rm{T}}{2}_{S}\) are binary variables indicating whether we observed strain-sharing of an individual species at time point T1 or T2, for all species combined. A random intercept for each individual species was added as well as for village membership and person.
In both models, ârelationshipâ is a dummy variable indicating the presence (or absence) of a tie between the pair of people, and M is the Mahalanobis distance calculated on the following covariates:
$$\begin{array}{c}M={\rm{M}}{\rm{a}}{\rm{h}}{\rm{a}}{\rm{l}}{\rm{a}}{\rm{n}}{\rm{o}}{\rm{b}}{\rm{i}}{\rm{s}}({\rm{a}}{\rm{g}}{\rm{e}},{\rm{s}}{\rm{e}}{\rm{x}},{\rm{B}}{\rm{M}}{\rm{I}},{\rm{B}}{\rm{r}}{\rm{i}}{\rm{s}}{\rm{t}}{\rm{o}}{\rm{l}}\,{\rm{s}}{\rm{t}}{\rm{o}}{\rm{o}}{\rm{l}}\,{\rm{s}}{\rm{c}}{\rm{a}}{\rm{l}}{\rm{e}},\\ \,\,{\rm{h}}{\rm{o}}{\rm{u}}{\rm{s}}{\rm{e}}{\rm{h}}{\rm{o}}{\rm{l}}{\rm{d}}\,{\rm{w}}{\rm{e}}{\rm{a}}{\rm{l}}{\rm{t}}{\rm{h}}\,{\rm{i}}{\rm{n}}{\rm{d}}{\rm{e}}{\rm{x}},{\rm{d}}{\rm{i}}{\rm{e}}{\rm{t}}\,{\rm{d}}{\rm{i}}{\rm{v}}{\rm{e}}{\rm{r}}{\rm{s}}{\rm{i}}{\rm{t}}{\rm{y}}\,{\rm{i}}{\rm{n}}{\rm{d}}{\rm{e}}{\rm{x}},\\ \,\,{\rm{m}}{\rm{e}}{\rm{d}}{\rm{i}}{\rm{c}}{\rm{a}}{\rm{t}}{\rm{i}}{\rm{o}}{\rm{n}}\,{\rm{u}}{\rm{s}}{\rm{a}}{\rm{g}}{\rm{e}},{\rm{w}}{\rm{a}}{\rm{t}}{\rm{e}}{\rm{r}}\,{\rm{s}}{\rm{o}}{\rm{u}}{\rm{r}}{\rm{c}}{\rm{e}},{\rm{b}}{\rm{u}}{\rm{i}}{\rm{l}}{\rm{d}}{\rm{i}}{\rm{n}}{\rm{g}}\,{\rm{I}}{\rm{D}})\end{array}$$
The pairwise Mahalanobis distance was calculated on the covariates matrix using the D2.dist function from the biotools R package53 (v.4.2). We also specified this model using the constituent variables, rather than the Mahalonobis distance (Supplementary Data 2).
Microbiome and social clustering
We use the Louvain and the Leiden methods as implemented in the igraph package to cluster participants along social and microbiome lines. Louvain clustering is based on greedy modularity optimization. Modularity is a scale value between â0.5 (non-modular clustering) and 1 (fully modular clustering) that measures the relative density of edges inside communities compared with edges outside communities. Optimizing this value theoretically results in the best possible grouping of the nodes of a given network. In cases where a pair shared too few SGBs to calculate a robust strain-sharing rate (fewer than ten), a strain-sharing rate of 0% was imputed to allow for proper weight-based clustering. This occurred in 0.45% of the pairwise comparisons (16,228 out of 3,560,769 comparisons), and just 838 of the 16,228 comparisons were from people in the same village. The adjusted Rand index was calculated with the mclust package (v.6.0.0)54.
For testing species differential abundance across network communities with the KruskalâWallis test, robustness checks ensuring that each social cluster had more than five people and the species was present in more than five people in the village were performed, and cases where this criterion was not met were excluded.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.