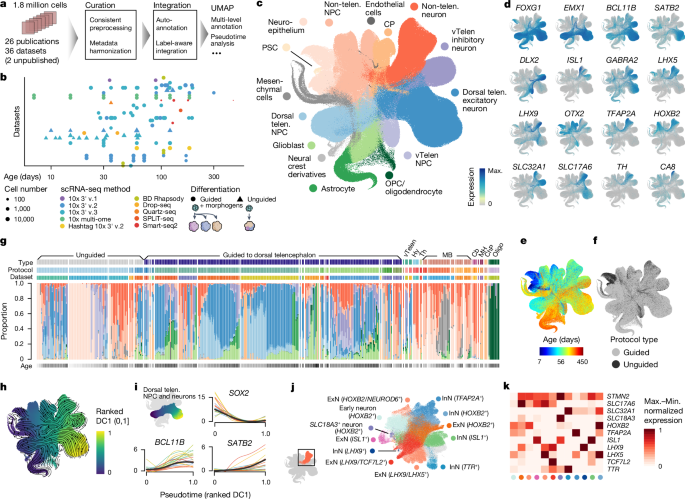
Metadata curation and harmonization of human neural organoid scRNA-seq datasets
We included 33 human neural organoid data from a total of 25 publications1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,26 plus three unpublished datasets in our atlas (Supplementary Table 1). We curated all neural organoid datasets used in this study through the sfaira78 framework (GitHub dev branch, 18 April 2023). For this, we obtained scRNA-seq count matrices and associated metadata from the location provided in the data availability section for every included publication or directly from the authors in case of unpublished data. We harmonized metadata according to the sfaira standards (https://sfaira.readthedocs.io/en/latest/adding_datasets.html) and manually curated an extra metadata column organoid_age_days, which described the number of days the organoid had been in culture before collection.
We next removed any non-applicable subsets of the published datasets: diseased samples or samples expressing disease-associated mutations (refs. 14,15,16,18,19,26), fused organoids (ref. 1), primary fetal data (refs. 10,23), hormone-treated samples (ref. 22), data collected before neural induction (refs. 3,20) and share-seq data (ref. 23). We harmonized all remaining datasets to a common feature space using any genes of the biotype âprotein_codingâ or âlncRNAâ from ensembl79 release 104 while filling any genes missing in a dataset with zero counts. On average, 50% of the full gene space (36,842 genes) was reported in each of the constituent datasets. We then concatenated all remaining datasets to create a single AnnData80 object.
Preprocessing of the HNOCA scRNA-seq data
All processing and analyses were carried out using scanpy81 (v.1.9.3) unless indicated otherwise. For quality control and filtering of HNOCA, we removed any cells with fewer than 200 genes expressed. We next removed outlier cells in terms of two quality control metrics: the number of expressed genes and percentage mitochondrial counts. To define outlier cells on the basis of each quality control metric, z-transformation is first applied to values across all cells. Cells with any z-transformed metric less than â1.96 or greater than 1.96 are defined as outliers. For any dataset collected using the v.3 chemistry by 10X Genomics, which contains more than 500 cells after the filtering, we fitted a Gaussian distribution to the histogram denoting the number of expressed genes per cell. If a bimodal distribution was detected, we removed any cell with fewer genes expressed than defined by the valley between the two maxima of the distribution. We then normalized the raw read counts for all Smart-seq2 data by dividing it by the maximum gene length for each gene obtained from BioMart. We next multiplied these normalized read counts by the median gene length across all genes in the datasets and treated those length-normalized counts equivalently to raw counts from the datasets obtained with the help of unique molecular identifiers in our downstream analyses.
As a next step we generated a log-normalized expression matrix by first dividing the counts for each cell by the total counts in that cell and multiplying by a factor of 1,000,000 before taking the natural logarithm of each countâ+â1. We computed 3,000 highly variable features in a batch-aware manner using the scanpy highly_variable_genes function (flavorâ=ââseurat_v3â, batch_keyâ=ââbio_sampleâ). Here, bio_sample represents biological samples as provided in the original metadata of the datasets. On average, 72% of the 3,000 highly variable genes were reported in each of the constituent HNOCA datasets. We used these 3,000 features to compute a 50-dimensional representation of the data using principal component analysis (PCA), which in turn we used to compute a k-nearest-neighbour (kNN) graph (n_neighborsâ=â30, metricâ=ââcosineâ). Using the neighbour graph we computed a two-dimensional representation of the data using UMAP82 and a coarse (resolution 1) and fine (resolution 80) clustering of the unintegrated data using Leiden83 clustering.
Hierarchical auto-annotation with snapseed
Snapseed is a scalable auto-annotation strategy, which annotates cells on the basis of a provided hierarchy of cell types and the corresponding cell type markers. It is based on enrichment of marker gene expression in cell clusters (high-resolution clustering is preferred), and data integration is not necessarily required.
In this study, we used snapseed to obtain initial annotations for label-aware integration. First, we constructed a hierarchy of cell types including progenitor, neuron and non-neural types, each defined by a set of marker genes (Supplementary Data 1). Next, we represented the data by the RSS3 to average expression profiles of cell clusters in the recently published human developing brain cell atlas27. We then constructed a kNN graph (kâ=â30) in the RSS space and clustered the dataset using the Leiden algorithm83 (resolution 80). For both steps, we used the graphical processing unit (GPU)-accelerated RAPIDS implementation that is provided through scanpy81,84.
For all cell type marker genes on a given level in the hierarchy, we computed the area under the receiver operating characteristic curve (AUROC) as well as the detection rate across clusters. For each cell type, a score was computed by multiplying the maximum AUROC with the maximum detection rate among its marker genes. Each cluster was then assigned to the cell type with the highest score. This procedure was performed recursively for all levels of the hierarchy. The same procedure was carried out using the fine (resolution 80) clustering of the unintegrated data to obtain cell type labels for the unintegrated dataset that were used downstream as a ground-truth input for benchmarking integration methods.
This auto-annotation strategy was implemented in the snapseed Python package and is available on GitHub (https://github.com/devsystemslab/snapseed). Snapseed is a light-weight package to enable scalable marker-based annotation for atlas-level datasets in which manual annotation is not readily feasible. The package implements three main functions: annotate() for non-hierarchical annotation of a list of cell types with defined marker genes, annotate_hierarchy() for annotating more complex, manually defined cell type hierarchies and find_markers() for fast discovery of cluster-specific features. All functions are based on a GPU-accelerated implementation of AUROC scores using JAX (https://github.com/google/jax).
Label-aware data integration with scPoli
We performed integration of the organoid datasets for HNOCA using the scPoli45 model from the scArches51 package. We defined the batch covariate for integration as a concatenation of the dataset identifier (annotation column âidâ), the annotation of biological replicates (annotation column âbio_sampleâ) as well as technical replicates (annotation column âtech_sampleâ). This resulted in 396 individual batches. The batch covariate is represented in the model as a learned vector of size five. We used the top three levels of the RSS-based snapseed cell type annotation as the cell type label input for the scPoli prototype loss. We chose the hidden layer size of the one-layer scPoli encoder and decoder as 1,024, and the latent embedding dimension as ten. We used a value of 100 for the âalpha_epoch_annealâ parameter. We did not use the unlabelled prototype pretraining. We trained the model for a total of seven epochs, five of which were pretraining epochs.
Benchmark of data integration methods
To quantitatively compare the organoid atlas integration results from several tools, we used the GPU-accelerated scib-metrics46,85 Python package (v.0.3.3) and used the embedding with the highest overall performance for all downstream analyses. We compared the data integration performance across the following latent representations of the data: unintegrated PCA, RSS3 integration, scVI49 (default parameters except for using two layers, latent space of size 30 and negative binomial likelihood) integration, scANVI50 (default parameters) integrations using snapseed level 1, 2 or 3 annotation as cell type label input, scPoli45 (parameters shown above) integrations using either snapseed level 1, 2 or 3 annotation or all three annotation levels at once as the cell type label input, scPoli45 integrations of metacells aggregated with the aggrecell algorithm (first used as âpseudocellâ3) using either snapseed level 1 or 3 annotation as the cell type label input to scPoli. We used the following scores for determining integration quality (each described in ref. 46): Leiden normalized mutual information score, Leiden adjusted rand index, average silhouette width per cell type label, isolated label score (average silhouette width-scored) and cell type local inverse Simpsonâs index to quantify conservation of biological variability. To quantify batch-effect removal, we used average silhouette width per batch label, integration local inverse Simpsonâs index, kNN batch-effect test score and graph connectivity. Integration approaches were then ranked by an aggregate total score of individually normalized (into the range of [0,1]) metrics. Before we carried out the benchmarking, we iteratively removed any cells from the dataset that had an identical latent representation to another cell in the dataset until no latent representation contained any more duplicate rows. This procedure removed a total of 3,293 duplicate cells (0.002% of the whole dataset) and was required for the benchmarking algorithm to complete without errors. We used the snapseed level 3 annotation computed on the unintegrated PCA embedding as ground-truth cell type labels in the integration.
Pseudotime inference
To infer a global ordering of differentiation state, we sought to infer a real-time-informed pseudotime on the basis of neural optimal transport47 in the scPoli latent space. We first grouped organoid age in days into seven bins ((0, 15], (15, 30], (30,60], (60, 90], (90, 120], (120, 150], (150, 450]). Next, we used moscot48 to solve a temporal neural problem. To score the marginal distributions on the basis of expected proliferation rates, we obtained proliferation and apoptosis scores for each cell with the method score_genes_for_marginals(). Marginal weights were then computed with
$$\exp (4\times ({\rm{prolif\_score}}-{\rm{apoptosis\_score}}))$$
The optimal transport problem was solved using the following parameters: iterationsâ=â25,000, compute_wasserstein_baselineâ=âFalse, batch_sizeâ=â1,024, patienceâ=â100, pretrainâ=âTrue, train_sizeâ=â1. To compute displacement vectors for each cell in age bin i, we used the subproblem corresponding to the [i, iâ+â1] transport map, except for the last age bin, where we used the subproblem [iâââ1,i]. Displacement vectors were obtained by subtracting the original cell distribution from the transported distribution. Using the velocity kernel from CellRank86 we computed a transition matrix from displacement vectors and used it as an input for computing diffusion maps87. Ranks on negative diffusion component 1 were used as a pseudotemporal ordering.
Preprocessing of the human developing brain cell atlas scRNA-seq data
The cell ranger-processed scRNA-seq data for the primary atlas27 were obtained from the link provided on its GitHub page (https://storage.googleapis.com/linnarsson-lab-human/human_dev_GRCh38-3.0.0.h5ad). For further quality control, cells with fewer than 300 detected genes were filtered out. Transcript counts were normalized by the total number of counts for that cell, multiplied by a scaling factor of 10,000 and subsequently natural-log transformed. The feature set was intersected with all genes detected in the organoid atlas and the 2,000 most highly variable genes were selected with the scanpy function highly_variable_genes using âDonorâ as the batch key. An extra column of âneuron_ntt_labelâ was created to represent the automatic classified neural transmitter transporter subtype labels derived from the âAutoAnnotationâ column of the cell cluster metadata (https://github.com/linnarsson-lab/developing-human-brain/files/9755350/table_S2.xlsx).
Reference mapping of the organoid atlas to the primary atlas
To compare our organoid atlas with data from the primary developing human brain, we used scArches51 to project it to the above mentioned primary human brain scRNA-seq atlas27. We first pretrained a scVI model49 on the primary atlas with âDonorâ as the batch key. The model was constructed with following parameters: n_latentâ=â20, n_layersâ=â2, n_hiddenâ=â256, use_layer_normâ=ââbothâ, use_batch_normâ=âânoneâ, encode_covariatesâ=âTrue, dropout_rateâ=â0.2 and trained with a batch size of 1,024 for a maximum or 500 epochs with early stopping criterion. Next, the model was fine-tuned with scANVI50 using âSubregionâ and âCellClassâ as cell type labels with a batch size of 1,024 for a maximum of 100 epochs with early stopping criterion and n_samples_per_labelâ=â100. To project the organoids atlas to the primary atlas, we used the scArches51 implementation provided by scvi-tools88,89. The query model was fine-tuned with a batch size of 1,024 for a maximum of 100 epochs with early stopping criterion and weight_decayâ=â0.0.
Bipartite weighted kNN graph reconstruction
With the primary reference27 and query (HNOCA) data projected to the same latent space, an unweighted bipartite kNN graph was constructed by identifying 100 nearest neighbours of each query cell in the reference data with either PyNNDescent or RAPIDS-cuML (https://github.com/rapidsai/cuml) in Python, depending on availability of GPU acceleration. Similarly, a reference kNN graph was also built by identifying 100 nearest neighbours of each reference cell in the reference data. For each edge in the reference-query bipartite graph, the similarity between the reference neighbours of the two linked cells, defined as A and B, respectively, is represented by the Jaccard index:
$$J(A,B)=\frac{| A\cap B| }{| A\cup B| }.$$
The square of Jaccard index was then assigned as the weight of the edge, to get the bipartite weighted kNN graph between the reference and query datasets.
wkNN-based primary developing brain atlas label transfer to HNOCA cells
Given the wkNN estimated between primary reference27 and query (HNOCA), any categorical metadata label of reference can be transferred to query cells by means of majority voting. In brief, for each category, its support was calculated for each query cell as the sum of weights of edges that link to reference cells in this category. The category with the largest support was assigned to the query cell.
To get the final regional labels for the non-telencephalic NPCs and neurons, as well as the NTT labels for non-telencephalic neurons, constraints were added to the transfer procedure. For regional labels, only the non-telencephalic regions, namely diencephalon, hypothalamus, thalamus, midbrain, midbrain dorsal, midbrain ventral, hindbrain, cerebellum, pons and medulla, were considered valid categories to be transferred. The label-transfer procedure was only applied to the non-telencephalic NPCs and neurons in HNOCA. Before any majority voting was done, the support scores of each valid category across all non-telencephalic NPCs and neurons in HNOCA were smoothed with a random-walk-with-restart procedure (restart probability alpha, 85%). Next, a hierarchical label transfer, which takes into account the structure hierarchy, was applied. First, the considered regions were grouped into diencephalon, midbrain and hindbrain, with a support score of each structure as its score summed up with scores of its substructures. Majority voting was applied to assign each cell to one of the three structures. Next, a second majority voting was applied to only consider the substructures under the assigned structure (for example, hypothalamus and thalamus for diencephalon).
For NTT labels, we first identified valid region-NTT label pairs in the reference on the basis of the provided NTT labels in the reference neuroblast and neuron clusters and their most common regions. Here, the most common regions were re-estimated in a hierarchical manner to the finest resolution mentioned above. Next, when transferring NTT labels, for each non-telencephalic neuron with the regional label transferred, only NTT labels that were considered valid for the region were considered during majority voting.
Stage-matching analysis
To match telencephalic NPCs and neurons in HNOCA to developmental stages, we used the recently published human neocortical development atlas30 as the reference. The processed single nucleus RNA-seq data were obtained from its data portal (https://cell.ucsf.edu/snMultiome/). Given the âclassâ, âsubclassâ and âtypeâ labels in the provided metadata as annotations, and âindividualâ as the batch label, scPoli was applied for label-aware data integration. Next, data representing different developmental stages were split. For each stage, Louvain clustering based on the scPoli latent representation (resolution, 5) was applied. Clusters of all stages were pooled, and highly variable genes were identified on the basis of coefficient of variations as described in this page: https://pklab.med.harvard.edu/scw2014/subpop_tutorial.html. Finally, every one of HNOCA telencephalic NPCs and neurons were correlated to each cluster across the identified highly variable genes. The stage label of the best-correlated cluster was assigned to the query HNOCA cell.
To extend the analysis to other neuronal cell types, the second-trimester multiple-region human brain atlas29 was also introduced. The processed count matrices and metadata were obtained from the NeMO data portal (https://data.nemoarchive.org/biccn/grant/u01_devhu/kriegstein/transcriptome/scell/10x_v2/human/processed/counts/). Given the âcell_typeâ label of the provided metadata as the annotation and âindividualâ as the batch label, scPoli was run for label-aware data integration. Louvain clustering was applied to the scPoli latent representation to identify clusters (resolution, 20). Similarly, Louvain clustering with a resolution of 20 was also applied to the first-trimester multiple-region human brain atlas27 on the basis of the scANVI latent representation we generated earlier. Average expression profiles were calculated for all the clusters, and highly variable genes were identified using the same procedure as above for clusters of the two primary atlases combined. Next, every NPC and neuron in HNOCA was correlated to the average expression profiles of those clusters. The best-correlated first- and second-trimester clusters, as well as the correlations, were identified. The differences between the two correlations were used as the metrics to indicate the stage-matching preferences of NPCs and neurons in HNOCA.
Presence scores and max presence scores of cells in the primary developing brain atlas
Given a reference dataset and a query dataset, the presence score is a score assigned to each cell in the reference, which describes the frequency or likelihood of the cell type or state of that reference cell appearing in the query data. In this study, we calculated the presence scores of primary atlas cells in each HNOCA dataset to quantify how frequently we saw a cell type or state represented by each primary cell in each of the HNOCA datasets.
Specifically, for each HNOCA dataset, we first subset the wkNN graph to only HNOCA cells in that dataset. Next, the raw weighted degree was calculated for each cell in the primary atlas, as the sum of weights of the remaining edges linked to the cell. A random-walk-with-restart procedure was then applied to smooth the raw scores across the kNN graph of the primary atlas. In brief, we first represented the primary atlas kNN graph as its adjacency matrix (A), followed by row normalization to convert it into a transition probability matrix (P). With the raw scores represented as a vector s0, in each iteration t, we generated st as
$${s}_{t}=\alpha {{\bf{s}}}_{0}+(1-\alpha ){P}^{T}{s}_{t-1}$$
This procedure was performed 100 times to get the smooth presence scores that were subsequently log transformed. Scores lower than the 5th percentile or higher than the 95th percentile were trimmed. The trimmed scores were normalized into the range of [0,1] as the final presence scores in the HNOCA dataset.
Given the final presence scores in each of the HNOCA datasets, the max presence scores in the whole HNOCA data were then easily calculated as the maximum of all the presence scores for each cell in the primary atlas. A large (close to one) max presence score indicates a high frequency of appearance for the cell type or state in at least one HNOCA dataset whereas a small (close to zero) max presence score suggests under-representation in all the HNOCA datasets.
Cell type composition comparison among morphogen usage using scCODA
To test the cell type compositional changes on admission of certain morphogens from different organoid differentiation protocols, we used the pertpy90 implementation of the scCODA algorithm91. scCODA is a Bayesian model for detecting compositional changes in scRNA-seq data. For this, we have extracted the information about the added morphogens from each differentiation protocol and grouped them into 15 broad molecule groups on the basis of their role in neural differentiation (Supplementary Table 1). These molecule groups were used as a covariate in the model. The region labels transferred from the primary atlas were used as labels in the analysis (cell_type_identifier). For cell types without regional identity, the cell type labels presented in Fig. 1c were used. Pluripotent stem cells and neuroepithelium cells were removed from the analysis because they are mainly present in the early organoid stages. We used bio_sample as the sample_identifier. We ran scCODA sequentially with default parameters, using No-U-turn sampling (run_nuts function) and selecting each cell type once as a reference. We used a majority vote-based system to find the cell types that were credibly changing in more than half of the iterations.
Cell type composition comparison among morphogen usage using regularized linear regression
To complement the composition analysis conducted with scCODA, we devised an alternative approach to test for differential composition using regularized linear regression. We fit a generalized linear model with the region composition matrix as the response Y and molecule usage as independent variables X:
$$Y \sim X{\boldsymbol{\beta }}$$
The model was fit with lasso regularization (alphaâ=â1) using Gaussian noise and an identity link function. The regularization parameter lambda was automatically determined through cross-validation as implemented in the function cv.glmnet() from the glmnet92 R package. All non-zero coefficients β were considered as indications of enrichment and depletion.
DE analysis between HNOCA neural cell types and their primary counterparts and functional enrichment analysis
To study the transcriptomic differences between organoid and primary cells, we subset HNOCA using the final level 1 annotation to cells labelled âNeuronâ. We furthermore subset the human developing brain atlas to cells that had been assigned a valid label in the neuron_ntt_label annotation column. We added an extra two datasets of fetal cortical cells from ref. 39 and ref. 28. For the data from ref. 39, we subset the data to cells labelled âfetalâ and estimated transcripts per million reads for each gene in each cell using RSEM93 given the STAR94 mapping results. We then computed a PCA, a kNN graph, UMAP and Leiden clustering (resolution 0.2) using scanpy. We then selected the cluster with the highest STMN2 and NEUROD6 expression as the cortical neuron cluster and used only those cells. For the data from ref. 28 we subset the datasets to cells annotated as âNeuronalâ in Supplementary Table 5 (âCortex annotationsâ) of their publication and computed a PCA, neighbourhood graph and UMAP to visualize the dataset. We found that only samples from the individuals CS14_3, CS20, CS22 and CS20 contained detectable expression of STMN2 and NEUROD6 so we subset the dataset further to only cells from those individuals.
To compute DE between HNOCA cells and their primary counterparts, we first aggregated cells of the same regional neural cell type into pseudobulk samples by summing the counts for every sample (annotation columns, âbatchâ for HNOCA; âSampleIDâ for the human developing brain atlas; âsampleâ for ref. 39 and âindividualâ for ref. 28) using the Python implementation of decoupler95 (v.1.4.0) while discarding any samples with fewer than ten cells or 1,000 total counts. We then subsetted the feature space to the intersection of features of all datasets and removed any cells with fewer than 200 genes expressed. We further removed any genes expressed in less than 1% of neurons in HNOCA and any genes located on the X and Y chromosomes. Out of the remaining 11,636 genes, on average, 99% were reported in each of the constituent HNOCA datasets. For each regional neural cell type, we removed any sample from the pseudobulk data that was associated with an organoid differentiation assay with fewer than two total samples or fewer than 100 total cells. We next used edgeR96 to iteratively compute DE genes between each organoid differentiation protocol and primary cells of the matching regional neural cell types for every regional neural cell type while correcting for organoid age in days, number of cells per pseudobulk sample, median and standard deviation of the number of detected genes per pseudobulk sample. We used the data from ref. 27 (the human developing brain atlas mentioned above), ref. 28 and ref. 39 as primary data for the DE comparison in the cell type âDorsal Telencephalic Neuron NT-VGLUTâ, whereas for all other cell types we used the human developing brain atlas as the fetal dataset. We used the edgeR genewise negative binomial generalized linear model with quasi-likelihood F-tests. We deemed a gene significantly DE if its false-discovery rate (BenjaminiâHochberg) corrected P value was smaller than 0.05 and it had an absolute log2-fold change above 0.5. We used the GSEApy97 Python package to carry out functional enrichment analysis in our DE results using the âGO_Biological_Process_2021â gene set.
To evaluate the effect of different primary datasets on the DE results, we computed the DE between Dorsal Telencephalic Neuron NT-VGLUT from the HNOCA subset generated with the protocol from ref. 6 and the matching cell type from the Braun et al.27 primary dataset as well as the data from ref. 28. To prevent technology effects to affect this analysis, we only used cells generated with the 10X Genomics 3â² v.2 protocol in this comparison. We generate pseudobulk samples as described above and corrected organoid age in days and number of cells per pseudobulk sample in the DE comparison. We used the same edgeR-based procedure and cut-offs as described above. We used the scipy fcluster method to cluster genes on the basis of their log-fold changes in the two primary datasets. We grouped clusters to represent consistently upregulated, consistently downregulated and three different inconsistently regulated groups of genes. We computed functional enrichment of each gene group as described above.
To evaluate the effect of different organoid datasets on the protocol-based DE analysis, we computed DE between Dorsal Telencephalic Neuron NT-VGLUT of every organoid publication (further split by protocol, where more than one protocol was used in a publication) and the matching cell type in the dataset from ref. 27. We computed pseudobulk samples and carried out the DE analysis using the same procedure and cut-offs as in the protocol-based DE analysis.
Transcriptomic similarity between HNOCA neural cell types and their primary counterparts in the human developing brain atlas
To estimate the transcriptomic similarity between neurons in HNOCA and the human developing brain atlas27, we first summarized the average expression of each neural cell type in the primary reference, as well as in each dataset of HNOCA. For each HNOCA dataset, only neural cell types with at least 20 cells were considered. Highly variable genes were identified across the neural cell types in the primary reference using a Chi-squared test-based variance ratio test on the generalized linear model with Gamma distribution (identity link), given coefficient of variance of transcript counts across neural cell types as the response and the reciprocal of average transcript count across neural cell types as the independent variable. Genes with BenjaminiâHochberg adjusted P values less than 0.01 were considered as highly variable genes. Similarity between one neural cell type in the primary atlas and its counterpart in each HNOCA dataset was then calculated as the Spearman correlation coefficient across the identified highly variable genes.
To estimate the similarity of the core transcriptomic identity, which is defined by the coexpression of transcription factors, the highly variable genes were subset to only transcription factorsfor calculating Spearman correlations. The list of transcription factors was retrieved from the AnimalTFDB v.4.0 database98.
To identify metabolically stressed cells in the datasets, we used the scanpy score_genes function with default parameters to score the âcanonical glycolysisâ gene set obtained from the enrichR GO_Biological_Process_2021 database across all neuronal cells from HNOCA and refs. 27,28,39.
To estimate the significance of the difference between the correlation of glycolysis scores and whole transcriptomic similarities, and the correlation of glycolysis scores and core transcriptomic identity similarities, we generated 100 subsets of highly variable genes, each with the same size as the highly variable transcription factor. Transcriptomic similarities were calculated on the basis of those subsets, and then correlated with the glycolysis scores.
Heterogeneity of the telencephalic trajectories
To characterize heterogeneity of telencephalic NPCs and neurons in HNOCA, we first transferred the cell type labels (as indicated as the âtypeâ label in the given metadata) from the human neocortical development atlas to the HNOCA telencephalic NPCs, intermediate progenitor cells and neurons, on the basis of transcriptomic correlation. In brief, each primary atlas cluster we obtained as mentioned above was assigned to a cell type as the most abundant cell type among cells in the cluster. The label of the best-correlated primary cluster was then transferred to every query cell. Given the transferred label, together with the level 2 cell type annotation shown in Fig. 1c, as the annotation label, scPoli was applied to the telencephalic subset of HNOCA for data integration.
To benchmark how well different integration strategies recover the neuron subcell type heterogeneity, we generated four different clustering labels: (1) Louvain clustering (resolution, 2) with the original scPoli latent representation; (2) Louvain clustering (resolution, 2) with the updated scPoli representation; (3) Louvain clustering (resolution, 2) with PCA of HNOCA telencephalic subset (based on scaled expression of 3,000 highly variable genes of the telencephalic subset with flavorâ=ââseuratâ) and (4) Louvain clustering (resolution, 1) for each sample separately (each with 3,000 highly variable genes identified with flavorâ=ââseuratâ, followed by data scale and PCA). Next, for each sample with at least 500 dorsal telencephalic neurons, the adjusted mutual information scores were calculated between each of those four clustering labels with the transferred cell type label mentioned above as the gold standard, across the dorsal telencephalic neurons as annotated as the level 2 annotation.
To create a comprehensive primary atlas of dorsal telencephalic neurons for DE analysis between neural organoids and primary tissues, we subset dorsal telencephalic neurons or neocortical neurons from four different primary atlases27,28,29,30. For ref. 28, cells in five author-defined clusters (60, 57, 79, 45, 65) with high expression of MAP2, DCX and NEUROD6 were selected. For ref. 29, cells with the following âclusterv2 – finalâ labels were selected: âNeuron_28â, âNeuron_34â, âGW19_2_29NeuronNeuronâ, âNeuron_30â, âNeuron_66Neuronâ, âGW18_2_42NeuronNeuronâ, âNeuron_33â, âNeuron_39Neuronâ, âNeuron_35â, âNeuron_63Neuronâ, âNeuron_9â, âNeuron_11â, âNeuron_20â, âNeuron_22â, âNeuron_5Neuronâ, âNeuron_21â, âNeuron_18â, âNeuron_101Neuronâ, âNeuron_17â, âNeuron_19â, âNeuron_16â, âNeuron_50Neuronâ, âNeuron_12â, âNeuron_13â, âNeuron_68Neuronâ, âNeuron_100Neuronâ, âNeuron_25â, âNeuron_27â, âNeuron_53Neuronâ, âNeuron_23â, âNeuron_26â, âNeuron_24â, âNeuron_102Neuronâ, âNeuron_72Neuronâ, âNeuron_15â, âNeuron_29â and âNeuron_35Neuronâ on the basis of their high expression of NEUROD6 and FOXG1. For ref. 27, cells dissected from dorsal telencephalon that were annotated as neurons with and only with the VGLUT NTT label were selected. For ref. 30, cells annotated as excitatory neurons were selected. The curated clusters of the Wang et al. primary atlas, as described earlier, were also subset to those with excitatory neuron labels. The selected dorsal telencephalic neuron subsets of the atlases were merged into the joint neocortical neuron atlas.
Next, cells in the joint neocortical neuron atlas were correlated with the average expression profile of each excitatory neuron cluster of the Wang et al. atlas30. The cluster label of the best-correlated cluster was assigned to each cell in the joined neocortical neuron atlas, so that cell cluster labels were harmonized for all cells in the atlas. Label-aware data integration was then performed using scPoli45. On the basis of the scPoli latent representation, Louvain clustering was performed on the joint neocortical neuron atlas (resolution, 1). This cluster label was transferred to the dorsal telencephalic neurons in HNOCA with max-correlation manner across highly variable genes defined on average transcriptomic profiles of clusters in the joint neocortical neuron atlas.
Reference mapping of the neural organoid morphogen screen scRNA-seq data to the human developing brain atlas and HNOCA
We used scArches to map scRNA-seq data from the neural organoid morphogen screen to both the scANVI model of the human developing brain atlas27 and the scPoli model of the HNOCA. In both cases, the âdatasetâ field of the screen data was used as the batch covariate, which indicates belonging to one of the three categories: âorganoid screenâ, âsecondary organoid screenâ or âfetal striatum 21pcwâ. For mapping to the primary reference, we used the scvi-tools implementation of scArches without the use of cell type annotations and trained the model for 500 epochs with weight_decay of 0 and otherwise default parameters. For mapping to HNOCA we used scArches through scPoli and trained the model for 500 epochs without unlabelled prototype training.
Retrieval and harmonization of disease-modelling human neural organoid scRNA-seq datasets
We included 11 scRNA-seq datasets of neural organoids, which were designed to model 10 different neural diseases including microcephaly56, amyotrophic lateral sclerosis43, Alzheimerâs disease57, autism42, FXS58, schizophrenia59, neuronal heterotopia60,61, PittâHopkins syndrome62, myotonic dystrophy63 and glioblastoma64. Count matrices and metadata were directly downloaded for the ten datasets with processed data provided in the Gene Expression Omnibus or ArrayExpress. For the dataset with only FASTQ files available56, we downloaded the FASTQ files and used Cell Ranger (v.4.0) to map reads to the human reference genome and transcriptome retrieved from Cell Ranger website (GRCh38 v.3.0.0) for gene expression quantification. All datasets were concatenated together with anndata in Python (joinâ=ââinnerâ). For each dataset, samples were grouped into either âdiseaseâ or âcontrolâ as their disease status, with âdiseaseâ representing data from patient cell lines, mutant cell lines with disease-related alleles, cells carrying targeting guide RNAs (gRNAs) in CRISPR-based screen and tumour-derived organoids. and âcontrolâ representing data from healthy cell lines, mutation-corrected cell lines and cells carrying only non-targeting gRNAs in a CRISPR-based screen.
Projection and label transfer-based annotation of the disease-modelling dataset
To compare the disease-modelling atlas with the integrated HNOCA, we used scArches51 to project it to the HNOCA as well as the first-trimester primary human brain scRNA-seq atlas27. For projecting to the primary atlas, the same implementation as mentioned above to map HNOCA to the atlas was used. For projecting to HNOCA, the query model was based on the scPoli model pretrained with the HNOCA data, and fineturned with a batch size of 16,384 for a maximum of 30 epochs with 20 pretraining epochs. A nearest neighbour graph was created for the disease-modelling atlas on the basis of the projected latent representation to HNOCA with scanpy (default parameters), with which a UMAP embedding was created with scanpy (default parameters).
Next, for both HNOCA and the disease-modelling atlas, cells were represented by the concatenated representation of HNOCA-scPoli and primary-scANVI models. A bipartite wkNN graph was then reconstructed as mentioned above, by identifying 50 nearest neighbours in HNOCA for each disease-modelling atlas cell. On the basis of the bipartite wkNN, the majority voting-based label transfer was applied to transfer the four levels of hierarchical cell type annotation and regional identity to the disease-modelling atlas.
Reconstruction of matched HNOCA metacells
For each cell in the disease-modelling atlas, a matched HNOCA metacell was reconstructed on the basis of the above mentioned bipartite wkNN. In brief, for a query cell i and a gene j measured in HNOCA, its matched metacell expression of j, denoted as \({{e}}_{{ij}}^{{\prime} }\), is calculated as:
$${e}_{{ij}}^{{\prime} }=\frac{{\sum }_{k\subseteq {N}_{i}}{w}_{{ik}}{e}_{{kj}}}{{\sum }_{k\subseteq {N}_{i}}{w}_{{ik}}}$$
Here, Ni represents all HNOCA nearest neighbours of the query cell ci, wik represents the edge weight between query cell i and reference cell k, and ekj represents expression level of gene j in reference cell k.
Given the matched HNOCA metacell transcriptomic profile, the similarity between a query cell and its matched cell state in HNOCA is then calculated as the Spearman correlation between the query cell transcriptomic profile and its matched HNOCA metacell transcriptomic profile.
Re-analysis of GBM-2019 and FXS-2021 datasets
To analyse the glioblastoma organoid dataset (GBM-2019), cells from the publication were subset from the integrated disease-modelling atlas. Using scanpy, highly variable genes were identified with default parameters. The log-normalized expression values of the highly variable genes were then scaled across cells, the truncated PCA was performed with the top 20 principal components used for the following analysis. Next, harmonypy, the Python implementation of harmony99, was applied to integrate cells from different samples. On the basis of the harmony-integrated embeddings, the neighbour graph was reconstructed. UMAP embeddings and Louvain clusters (resolution, 0.5) were created on the basis of the nearest neighbour graph. Among the 12 identified clusters, cluster-7 and cluster-0, the two clusters with the highest AQP4 expression, were selected for the following DE analysis.
To analyse the FXS dataset (FXS-2021), cells from the publication were subset from the integrated disease-modelling atlas. The same procedure of highly variable gene identification, data scaling and PCA as the GBM-2019 dataset was applied. Next, the nearest neighbour graph was created directly on the basis of the top 20 principal components. UMAP embeddings and Louvain clusters (resolution, 1) were then created on the basis of the reconstructed nearest neighbour graph. Among the 30 clusters, cluster-17 and cluster-23, which express EMX1 and FOXG1 and were largely predicted to be dorsal telencephalic NPCs and neurons according to the transferred labels from HNOCA, were selected for the following DE analysis.
F-test-based DE analysis for paired transcriptome
To compare expression levels of two groups of paired cells, the expression difference per gene of each cell pair is first calculated on the basis of the log-normalized expression values. Next, for each gene to test for DE, its variance over the calculated expression difference per cell pair (Ï2) is compared with the sum of squared of expression differences (di for gene i) normalized by the number of cell pairs:
$${s}_{0}^{2}=\frac{{\sum }_{i=1}^{n}{d}_{i}}{n}.$$
Here, an F-test is applied for the comparison, with fâ=âÏ2/s20, d.f.1â=ânâââ1 and d.f.2â=ân.
Construction of the HNOCA Community Edition by query-to-reference mapping
To construct the HNOCA-CE, we first collected raw count matrices and associated metadata of five more neural organoid studies. For two publications71,75, we obtained them from the sources listed in the âData availabilityâ section of the paper. For the remaining three publications72,73,74, count matrices and associated metadata were provided directly by the authors. We subset each dataset to the healthy control cells and removed any cells with fewer than 200 genes expressed. We subset the gene space of every dataset to the 3,000 HVGs of HNOCA while filling the expression of missing genes in the community datasets with zeros. On average, 23% of genes with zero expression were added per dataset. We instantiated a mapping object from the HNOCA-tools package (at commit fe38c52) using the saved scPoli45 model weights from the HNOCA integration. Using the map_query method of the mapper instance, we projected the community datasets to HNOCA. We used the following training hyperparameters: retrainâ=ââpartialâ, batch_sizeâ=â256, unlabeled_prototype_trainingâ=âFalse, n_epochsâ=â10, pretraining_epochsâ=â9, early_stopping_kwargsâ=âearly_stopping_kwargs, etaâ=â10, alpha_epoch_annealâ=â10. We computed the wkNN graph using the compute_wknn method of the mapper instance with kâ=â100. We transferred the final level_2 cell type labels from HNOCA to the community datasets using this neighbour graph. To obtain the combined representation of HNOCA-CE, we projected HNOCA together with the added community datasets through the trained model and computed a neighbour graph and UMAP from the resulting latent representation.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.