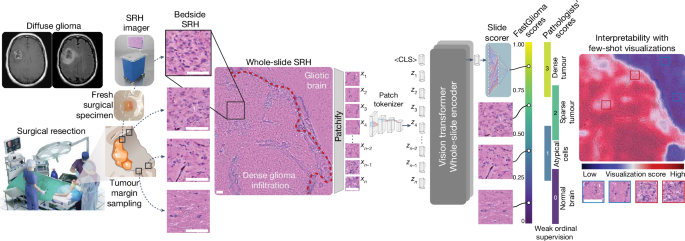
Study design
We had three main objectives for this study: (1) train a vision transformer model on a large and diverse dataset of SRH images using self-supervision to develop the first SRH visual foundation model; (2) fine-tune the visual foundation models to develop FastGlioma for detection and quantification of diffuse glioma infiltration in fresh, unprocessed surgical specimens; (3) validate FastGlioma in a prospective, multicentre, international cohort of patients with diffuse glioma and compare results to current surgical adjuncts. We adopted the common working definition of a foundation model: (1) any machine learning model that is (2) trained on a large and diverse dataset using (3) self-supervision at scale and (4) can be adapted to a wide range of downstream tasks13. We also added to this definition (5) evidence of zero-shot generalization to new, unseen data. Foundation modelling had not been previously investigated in studies on the clinical applications of SRH and we focused on tumour infiltration as the most clinically important and ubiquitous problem in cancer surgery as the major downstream tasks. We aimed to design FastGlioma to detect microscopic tumour infiltration for all diffuse glioma molecular subtypes. A major data-centric contribution of this work was developing a multicentre, international, label-free SRH tumour-infiltration dataset annotated by expert neuropathologists. Preliminary results demonstrated the feasibility of generating this complex biomedical dataset4. Moreover, previous studies that combine SRH and AI were done such that the same imaging dataset was used both for human interpretation and AI model training42,44. Here we aimed to push the limits of AI-based computer vision performance in lower image resolution/faster image acquisition regimes at 10 times the speed of conventional SRH imaging. Finally, we aimed to demonstrate the feasibility of using FastGlioma as a surgical adjunct and compare tumour detection performance with existing image-guided and fluorescence-guided surgical adjuncts.
SRH imaging
All of the images in our study were acquired using intraoperative fibre-laser-based stimulated Raman scattering microscopy21,49. The NIO Imaging System (Invenio Imaging) was used for all training and testing data collection. We have provided a detailed description of the imager and laser configuration in previous studies20,49. In brief, a pump beam at 790ânm and a Stokes beam with a tuneable range from 1,015ânm to 1,050ânm was used to stimulate the surgical specimens. The settings allow for access to the Raman shift spectral range between 2,800âcmâ1 and 3,130âcmâ1. Images were acquired as 1,000 pixel-width strips with an imaging speed of 0.4âMpx per strip. In normal imaging mode, each strip row is acquired independently in a leftâright manner using a custom beam-scanning20,21. Two image channels are acquired sequentially at 2,845âcmâ1 (CH2 channel) and 2,930âcmâ1 (CH3 channel) Raman wavenumber shifts. A stimulated Raman signal at 2,845âcmâ1 represents the CH2 symmetric stretching mode of lipid-rich structures, such as myelinated axons. A second Raman peak at 2,930âcmâ1 corresponds to protein- and nucleic acid-rich regions such as the cell nucleus and collagen. As all SRH strips are acquired through standard horizontal line scanning20,21,49, low-resolution SRH images can be generated by directly downsampling SRH strip rows by a downsampling factor, such as 1/2, 1/4, 1/8 and so on. Halving the line sampling factor corresponds to a 2à imaging time savings. In fast imaging mode, single-channel images with a user-specified downsampling factor are acquired. The whole-slide SRH images are then split into 300âÃâ300 pixel patches without overlap using a sliding raster window over the full image. All models are trained using 16-bit, raw, greyscale SRH images. For the purposes of the study, SRH images were acquired as two-channel images (2,845âcmâ1, 2,930âcmâ1) for pathologistâs review to determine ground truth tumour-infiltration labels.
SRH dataset
Clinical SRH imaging began at the University of Michigan (UM) on 1 June 2015 following Institutional Review Board approval (HUM00083059). All patients with a suspected brain tumour were recruited for intraoperative SRH imaging in a prospective manner. The inclusion criteria were as follows: patients who were undergoing surgery for (1) suspected central nervous system tumour and/or (2) epilepsy, (3) subject or durable power of attorney was able to provide consent and (4) preoperative assessment that additional tumour specimens would be available in addition to what is required for clinical pathologic diagnosis. Exclusion criteria were (1) grossly inadequate tissue, (2) insufficient diagnostic tissue (for example, haemorrhagic, necrotic) or (3) imaging malfunction. A similar imaging protocol was implemented at 12 other medical centres with clinical SRH imaging deployed in their operating rooms. A total of 2,799 patients, 11,462 whole-slide SRH images and approximately 4âmillion unique 300âÃâ300 pixel SRH patches were included for SRH foundation model training. Dataset statistics and diagnostic information are provided in Extended Data Fig. 2.
SRH foundation model training
SRH foundation models consist of two modular components trained using self-supervision: the patch tokenizer and the whole-slide encoder.
Patch tokenizer training with hierarchical discrimination
In standard vision transformers, converting small, fixed-size image patches, such as 8âÃâ8 or 16âÃâ16 pixel patches, into tokens can be done by flattening. This tokenization strategy is not feasible due to the size of whole-slide SRH images (>6,000âÃâ6,000 pixels). We therefore developed a data-driven patch tokenization method that leverages the inherent patient-slide-patch hierarchy of SRH images to define a hierarchical discriminative learning task23. We previously demonstrated that hierarchical discrimination, called HiDisc, outperforms instance discrimination methods for biomedical microscopy computer vision tasks. HiDisc uses self-supervised contrastive learning such that positive image patches are defined based on a shared ancestry in the patient-slide-patient data hierarchy. The HiDisc loss is a summation of three losses, each of which corresponds to instance discrimination at a level of the patch-slide-patient hierarchy. We define the HiDisc loss at the level \({\ell }\) to be:
$${L}_{{\rm{HiDisc}}}^{{\ell }}=\sum _{i\in {\mathcal{I}}}\frac{-1}{| {{\mathcal{P}}}_{{\ell }}(i)| }\sum _{p\in {{\mathcal{P}}}_{{\ell }}(i)}log\frac{\exp ({z}_{i}\cdot {z}_{p}/\tau )}{{\sum }_{a\in {\mathcal{A}}(i)}\exp ({z}_{i}\cdot {z}_{a}/\tau )},$$
(1)
where \({\ell }\in \{{\rm{Patch}},{\rm{Slide}},{\rm{Patient}}\}\) is the level of discrimination, and I is the set of all images in the minibatch. \({{\mathcal{A}}}_{\ell }(i)\) is the set of all images in I except for the anchor image i,
$${{\mathcal{A}}}_{\ell }(i)={\mathcal{I}}\backslash \{i\},$$
(2)
and \({{\mathcal{P}}}_{{\ell }}(i)\) is a set of images that are positive pairs of i at the \({\ell }\) level,
$${{\mathcal{P}}}_{{\ell }}(i)=\{p\in {{\mathcal{A}}}_{{\ell }}(i):{{\rm{ancestry}}}_{{\ell }}(p)={{\rm{ancestry}}}_{{\ell }}(i)\},$$
(3)
where \({{\rm{ancestry}}}_{{\ell }}(\,\cdot \,)\) is the \({\ell }\)-level ancestry for the anchor patch. For example, patches xi and xj from the same patient would have the same patient ancestry, that is, \({{\rm{ancestry}}}_{{\rm{Patient}}}({x}_{i})={{\rm{ancestry}}}_{{\rm{Patient}}}({x}_{j})\). The component HiDisc losses calculate the same overall contrastive objective with positive pairs at different levels in the hierarchy. Finally, the complete HiDisc loss is the sum of the patch-, slide- and patient-level losses defined above:
$${{\mathcal{L}}}_{{\rm{HiDisc}}}=\sum _{{\ell }\in \{{\rm{Patch}},{\rm{Slide}},{\rm{Patient}}\}}{{\rm{\lambda }}}_{{\ell }}{L}_{{\rm{HiDisc}}}^{{\ell }},$$
(4)
where \({{\rm{\lambda }}}_{{\ell }}\) is a weighting hyperparameter for level \({\ell }\) in the total loss. As HiDisc is a self-supervised representation learning method, we used the full SRH dataset as shown in Extended Data Fig. 2a. We found that HiDisc patch tokenization improved classification performance compared with ImageNet transfer learning (Extended Data Fig. 3c).
Patch encoding was accomplished using the ResNet-34 architecture as the backbone feature extractor and a one-layer multilayer perceptron to project the embedding to 128-dimensional latent space for HiDisc self-supervised training50. We performed ablation studies over the batch size, learning rate and loss hyperparameters to optimize performance on the SRH7 dataset. The encoder was trained using a batch size of 512 and an AdamW optimizer with a learning rate of 0.001 on a cosine decay schedule with warmup for the first 10% of training iterations for a total of 100,000 iterations on the foundation SRH dataset. To train using the HiDisc loss, the mini-batches were constructed by first selecting 64 patients, followed by sampling two slides per patient, two patches per slide and finally applying two random augmentations per patch, yielding 512 patches. The patch, slide and patient losses were weighted equally, and the temperature was set to 0.7. All of the patch experiments were performed using mixed-precision and data parallelism on four NVIDIA A40 GPUs, taking up to 3 days. We performed additional ablation experiments with open-source foundational patch encoders to assess the quality of HiDisc feature learning compared with other pretrained models19 (Supplementary Table 4).
Whole-slide encoder
A major contribution of this work was developing an efficient and effective method for whole-slide self-supervised training with vision transformer architectures. The major advantage of vision transformers for whole-slide inference in computational pathology and optical imaging is their ability to handle large and variably sized images. The whole-slide self-supervised learning strategy is a Siamese architecture that requires two random transformations of the same whole-slide image. The slide-level transformation strategy is as follows. First, the whole slide is split into two mutually exclusive patch sets (splitting). Next, two random spatial crops are selected from the whole-slide image (cropping). Finally, 10â80% of patches from a crop are dropped (masking). This strategy is ideally suited for vision transformers because it allows for variable sized inputs and random dropping of patch tokens/spatial regions within a whole-slide image. After generating two transformed views, we then minimize a varianceâinvarianceâcovariance (VICReg) self-supervised objective function51. VICReg is well suited for whole-slide encoding because it is computationally efficient, does not require negative examples and maintains high expressivity by avoiding dimensional collapse52.
The whole-slide transformer consists of 2 hidden layers with dimension 512, with 4 attention heads per layer. The output of the transformer is distilled into a <CLS> token, with seven additional register tokens employed to stabilize training53. Positional information is learned concurrently in a Fourier feature positional embedding generator network54. The Fourier feature and MLP hidden dimension of this network are 96 and 36, respectively. For self-supervision purposes, a one-layer MLP was trained to project the embedding to 128-dimensional latent space. The VICReg objective was used for whole-slide self-supervised training, with the coefficients being 10, 10 and 1 for the variance, invariance and covariance losses, respectively. Pretraining was done with an effective batch size of 256 and the AdamW optimizer with a learning rate of 3âÃâ10â4 for 100 epochs on a single NVIDIA Titan V100 GPU. Checkpoints were saved every 10 epochs, with the optimal one selected using slide-level metrics on the histological brain tumour diagnosis task with a hold-out validation set. A schematic of SRH foundation model training is shown in Extended Data Fig. 3. Detailed model training configurations, including batch size, learning rate and other hyperparameters, are shown in Supplementary Table 6 and are available at GitHub (https://github.com/MLNeurosurg/fastglioma).
SRH foundation model evaluation
Validation of the foundation model was performed on a multiclass SRH brain tumour diagnostic task. This dataset consists of 3,560 whole-slide images from 896 patients (852,000 total patches). Diagnostic classes are normal brain, high-grade glioma (HGG), low-grade glioma (LGG), meningioma, pituitary adenoma, schwannoma and metastatic tumour. In all previous benchmarking studies, training required supervised filtering of nondiagnostic patches and patch-level average pooling for whole-slide inference, which is known to degrade performance42,43,44. Here we demonstrate that high-quality self-supervised patch and whole-slide representation learning with vision transformers bypasses the need for preprocessing, filtering or patch-level voting/averaging. We used nearest-neighbour classification (k-NN) for SRH foundation model evaluation. First, we generated whole-slide representations for both the training and testing data. Next, the k-NN classifier was used to match each slide in the testing dataset to the k most similar representations in the training dataset as determined by their cosine similarity. We set kâ=â10 in our experiments for all models to ensure consistent results. This enables us to determine a class prediction for each slide in the testing dataset. We then calculate the mean class accuracy (MCA) and mean average precision (mAP) for the seven-class task for slide metrics (Extended Data Fig. 4). Whole-slide representations were visualized using t-distributed stochastic neighbour embedding (t-SNE) to qualitatively assess slide representations with respect to tumour classes. Embeddings for k-NN and subsequent evaluations were generated on a single NVIDIA Titan V100 GPU.
Fine-tuning with ordinal representation learning
Our SRH foundation models were specifically developed to adapt to downstream diagnostic tasks for clinical decision support. Here we aimed to fine-tune the foundation model for the detection and quantification of tumour infiltration using intraoperative SRH imaging. While diffuse glioma infiltration is a continuous random variable, the majority of previous work modelled glioma infiltration as an ordinal variable4,55, such that expert pathologists score the degree of tumour infiltration on a discrete, ordered scale. We fine-tuned the foundation model using the glioma-infiltration dataset from a previous study4. The dataset consists of 161 surgical specimens imaged using SRH from 35 patients. The degree of tumour infiltration in each SRH image was scored on a scale from 0 to 3 by three independent expert neuropathologists, where 0 is no tumour present; 1 is mildly cellular tissue either due to reactive gliosis or with scattered atypical cells, without definitive tumour; 2 is tumour present but in mild/sparse density; and 3 is moderate to severe density of tumour cells. This dataset is approximately 100 times smaller than the SRH foundation model training dataset and approximately 10 times smaller than the calculated sample size for model testing. Owing to this extreme data sparsity for fine-tuning, we developed a general, data-efficient, few-shot ordinal representation learning method called ordinal metric learning. Ordinal metric learning aims to minimize the feature distance, or metric, between images with the same ordinal rank. Moreover, it implicitly learns to order images based on their ordinal label by performing a pairwise comparison between all images in a mini-batch. Ordinal metric learning accomplishes this by applying a binary cross entropy objective on the distance \({d}_{i,j}={s}_{i}-{s}_{j}\) between scores for all possible pairs of images in a mini-batch to enforce the image with the higher label is assigned a higher score. The following loss equation accomplishes this:
$${{\mathcal{L}}}_{{\rm{OrdinalMetric}}}=\sum _{i\in {\mathcal{I}}}\left\{\frac{1}{|{\mathcal{B}}(i)|}\sum _{b\in {\mathcal{B}}(i)}{\rm{BCE}}({d}_{i,b},{{\bf{1}}}_{i,b})\right\},$$
(5)
where
$${\rm{BCE}}(x,y)=y\cdot \log \sigma (x)+(1-y)\cdot \log (1-\sigma (x)),$$
(6)
and
$${{\bf{1}}}_{x,y}=\{\begin{array}{ll}1 & {\rm{if}}\,{l}_{x} > {l}_{y}\\ 0 & {\rm{otherwise}}\end{array},$$
(7)
\({\mathcal{I}}\) is the set of all images in the minibatch. \({\mathcal{B}}(i)\) is the set of all images in \({\mathcal{I}}\) except for those with the same label as the anchor image i, \({\mathcal{L}}(i)\), denoted as,
$${\mathcal{B}}(i)={\mathcal{I}}\backslash {\mathcal{L}}(i),$$
(8)
A schematic of ordinal metric learning is shown in Extended Data Fig. 4.
Ordinal metric learning was used to train the FastGlioma model and included fine-tuning the slide encoder and a one layer linear slide scorer. Tumour-infiltration labels were balanced by whole-slide oversampling of the minority classes during training. The model was trained with a batch size of 16 and adjusted learning rate of 1.875âÃâ10â5 for 100 epochs. The best checkpoint was selected using a hold-out validation set. To evaluate the SRH foundation model, a standard linear evaluation protocol was followed with only the slide scorer being trained. Our linear evaluation protocol is similar to other self-supervised visual representation learning methods, such as SimCLR56 or DINO57, where the visual feature extractor is frozen and a final classification/regression layer is trained.
Tumour-infiltration scoring metrics
To evaluate the performance of FastGlioma in distinguishing various levels of diffuse glioma infiltration, we employ two key metrics: mAUROC and mean absolute error (MAE). The MAE is calculated by passing the FastGlioma whole-slide logit through a sigmoid activation function to rescale between 0 to 1. Similarly, the ground truth labels, which range from 0 to 3, are also normalized to 0 to 1. We then compute the MAE by measuring the average absolute difference between the rescaled logits and the normalized labels. The mAUROC provides a straightforward metric to assess FastGliomaâs ability to discern between different degrees of tumour infiltration. mAUROC is calculated as the average of the AUROC for three binary classification tasks: 0 versus 123, 01 versus 23 and 012 versus 3. This metric reflects the ordinal label distribution and emphasizes the clinical diagnostic task.
Prospective testing of FastGlioma
Our prospective FastGlioma clinical testing included a primary and secondary end point. The primary end point was to validate FastGliomaâs ability to reproducibly and accurately detect tumour infiltration within SRH images across patient populations, demographics, medical centres and diffuse glioma subgroups. The secondary end point was to compare the performance of FastGlioma with the standard-of-care methods for intraoperative tumour-infiltration detection currently in use for brain tumour surgery.
Primary testing end point: SRH-based tumour-infiltration detection
Our primary study end point was to achieve a diagnostic performance for detecting diffuse glioma infiltration in SRH images on par with previous SRH classification tasks, such as intraoperative tissue diagnosis and molecular classification42,44. We designed the primary testing using the same principles as a single-arm, non-inferiority diagnostic clinical trial42,44. To obtain a minimum sample size estimate, we used previous studies that combined SRH and AI to classify normal brain versus any tumour tissue. Previously reported accuracy values range from 89.3 to 95.8% with an average value of 93.2% (±3.6%)42,43,44,55. We used this average value to define the expected performance, the equivalence/non-inferiority limit was set to 5%, the alpha value to 2% and the power to 90%, resulting in a sample size value of 565 SRH images obtained from surgical margins. We aimed to achieve this sample size for both IDH-wild-type and IDH-mutant diffuse gliomas to ensure generalizability and reproducibility across diffuse glioma molecular subtypes as defined by the WHO. The calculation resulted in a final minimum sample size of 1,130 surgical specimens. Prospective patient recruitment was continued until minimum sample sizes were reached in both IDH-mutant and IDH-wild-type cohorts. All sample size calculations were performed using the epiR package (v.2.0.46) in R (v.3.6.3). Ground-truth SRH tumour-infiltration labels were provided by the on-site study pathologists (M.P., M.M.-E., T.R.-P.). All pathologists were provided with written and video instructions for SRH tumour-infiltration scoring using the four-tiered system by our primary study pathologist (M.P.).
Secondary testing end point: FastGlioma comparison with image- and fluorescence-based surgical adjuncts for tumour-infiltration detection
Our secondary study end point was to compare the FastGlioma intraoperative workflow (experimental arm) with the two most common surgical adjuncts for identifying tumour infiltration intraoperatively (control arm) in a simulated prospective surgical trial. âSimulatedâ terminology is used because FastGlioma is not approved by the Food and Drug Administration or European Medicines Agency to guide treatment decisions, such as extent of tumour resections. However, we aimed to demonstrate the feasibility and safety of using FastGlioma to guide resections by predicting on surgical specimens sampled at the resection margin of patients with diffuse glioma. FastGlioma predictions in this setting produce the actionable information needed to guide resection and simulates the clinical setting that FastGlioma would be deployed. FastGlioma was compared in a head-to-head prospective comparison study to (1) image-guided surgery with MRI-based neuronavigation and (2) fluorescence-guided surgery with 5-ALA. Both methods have been shown to improve the extent of resection in randomized controlled trials28,29. In general, neuronavigation and 5-ALA fluorescence can indicate the presence of tumour infiltration but, in contrast to FastGlioma, do not quantify the degree of infiltration. For the purposes of this study and others30, tumour detection using neuronavigation or 5-ALA was treated as a binary indicator, for example, yes/no contrast enhancement, yes/no 5-ALA fluorescence. To perform a fair comparison between FastGlioma and the surgical adjuncts, we designed this secondary end point to differentiate normal brain tissue (score 0) versus dense tumour (score 3). We focused specifically on this task because errors are clinical high-risk errors and these tumour-infiltration scores are actionable and decisive: score 0 means stop resection, score 3 means continue resection if otherwise safe. Moreover, this strategy avoids biasing performance results in favour of FastGlioma, which provides a continuous score that can differentiate degrees of tumour infiltration. We aimed to show that FastGlioma was non-inferior to both neuronavigation and 5-ALA fluorescence for detecting tumour within surgical specimens collected at the margin of resection cavities during surgical resection. Details of generating the matched SRH/MRI/5-ALA specimen dataset as a subset of the primary testing endpoint data are described below.
Prospective testing dataset
Three medical centres acted as external FastGlioma testing sites: UCSF, NYU and MUV. Each medical centre prospectively enrolled patients for testing. Inclusion criteria were: (1) patient age, â¥18 years; (2) a suspected diffuse glioma on preoperative radiographic imaging; and (3) planned brain tumour resection. Exclusion criteria included: (1) aborted tumour resection; (2) non-glioma final pathology; and (3) SRH imager malfunction. We aimed to accurately simulate the clinical setting that FastGlioma would be implemented for surgical interventions. Study neurosurgeons were therefore instructed to sample surgical margins at their discretion to identify microscopic tumour infiltration within the tumour resection cavity. We aimed to provide as minimal instruction as possible to account for surgeon/user variability during FastGlioma testing. After intraoperative SRH imaging, surgical specimens were removed from the premade microscope slide and preserved in formalin for downstream tissue processing (Extended Data Fig. 1). Each SRH image was scored postoperatively by an onsite, board-certified neuropathologist with dedicated training and expertise in intraoperative SRH imaging. Our central neuropathologist (M.P.) provided verbal and video instructions for tumour-infiltration scoring. We used the previously developed and validated protocol for 0â3 tumour-infiltration scoring4. For the primary testing end point that is evaluated at the image level, SRH tumour-infiltration scores provided by the neuropathologists were used as the ground truth. For the secondary testing end point that is evaluated at the specimen level, neuronavigation coordinates, radiographic features (that is, contrast enhancement, FLAIR positive) and 5-ALA fluorescence status were recorded in real-time by a study technician for each specimen. Secondary end-point testing was completed at UCSF by a dedicated study technician (K.S.) and central neuropathologist (M.P.) to standardize all matched data collection. To optimize for the secondary testing endpoint, annotated data from UM, NYU and MUV were used to fine-tune FastGlioma. After intraoperative SRH imaging, the specimen was extracted from the premade microscopy slide and sent for downstream whole-slide/specimen analysis using H&E/immunohistochemistry testing as previously detailed4. Specimen-level ground truth tumour-infiltration scores were determined based on whole-slide analysis. This strategy allows for an unbiased comparison between all three surgical adjuncts.
FastGlioma versus cellularity-based tumour-infiltration scoring
The cellularity within the SRH whole-slide images was calculated to be the average number of cells per 300âÃâ300 pixel SRH patch. The number of cells was determined using an SRH single-cell segmentation model training using full supervision. Specifically, a Mask R-CNN model with a ResNet-50 backbone pre-trained on the Microsoft COCO dataset was fine-tuned on 1,000 annotated SRH patches of normal brain and 6 different brain tumour diagnoses58. The final model predictions were filtered with a non-maximal suppression algorithm to remove overlapping cell bounding boxes with >20% area and predictions with less than 80% confidence. Correlation between cellularity and FastGlioma tumour-infiltration score was calculated using Pearsonâs correlation coefficient. To evaluate whether cellularity can be used to detect diffuse glioma infiltration, the surrogate tumour-infiltration score for a whole slide was calculated using the cellularity value. This was then used to calculate the mAUROC across the three different tumour-infiltration tasks to compare with FastGlioma infiltration scores as shown in Extended Data Fig. 7.
Few-shot visualizations and model interpretability
We aimed to develop a whole-slide visualization method that can accurately and flexibly identify regions of tumour infiltration within SRH images to improve model interpretability. Studies on vision transformers have generally relied on plotting self-attention coefficients to generate data visualizations57. Unfortunately, this strategy does not guarantee uniformly high attention coefficients on foreground/tumour infiltrated regions and is known to produce spurious high attention coefficients in background regions53. We therefore developed a few-shot visualization strategy that uses a curated support set of expert physician-selected SRH patches, or keys, that include diverse examples of normal brain parenchyma and diffuse glioma subtypes. This strategy takes advantage of the representational power of the self-supervised patch tokenizer to identify similar SRH features within any given whole-slide field-of-view. Specifically, for any SRH patch query, xq, within a whole-slide SRH image, we calculate the dot product between the tokenized query patch zq and a support set of tokenized keys, S. We first determine whether the query patch is foreground/diagnostic by determining if the maximal dot product across the support set exceeds a threshold, Ï. If not, then the patch is classified as background. If the query dot product exceeds Ï for any patch in the support set, we then assign it a few-shot visualization score, sq. This is defined as the difference between the maximum dot product from the tumour exemplars in the support subset, \({S}_{{\rm{tumour}}}\), and the maximum dot product from the normal exemplars, \({S}_{{\rm{normal}}}\):
$${{\bf{s}}}_{{\bf{q}}}=\left\{\begin{array}{ll}{s}_{q}^{{\prime} } & {\rm{if}}\,\mathop{\max }\limits_{\forall p\in S}\,{\rm{sim}}({z}_{q},{z}_{p}) > \phi \\ {s}_{\min } & {\rm{otherwise}}\end{array}\right.,$$
(9)
where
$${s}_{q}^{{\prime} }=\mathop{\max }\limits_{\forall t\in {S}_{{\rm{tumour}}}}{\rm{sim}}({z}_{t},{z}_{q})-\mathop{\max }\limits_{\forall n\in {S}_{{\rm{normal}}}}{\rm{sim}}({z}_{n},{z}_{q}),$$
(10)
and sim is the cosine similarity, \({\rm{sim}}(x,y)=\frac{{x}^{{\rm T}}y}{\Vert x\Vert \Vert y\Vert }\) and Ï was 0.5 for our visualizations. This visualization strategy has the advantage of leveraging both the feature similarity between tumour patches and the dissimilarity between tumour and normal patches. If a patch has a high similarity to any of the tumour exemplars and high dissimilarity with the normal exemplars, then \({s}_{q}\mathrm{ > 0}\), and vice versa. Empirically, 10 or less patch exemplars per subset can yield high-quality and interpretable visualizations using FastGlioma. Moreover, this strategy demonstrates good zero-shot generalization to non-glioma brain tumour diagnoses without needing to add tumour-specific examples (for example, meningioma or medulloblastoma exemplars) to the support set, as shown in Extended Data Fig. 10.
Computational hardware and software
SRH images were processed using an Intel Core i76700K Skylake QuadCore 4.0 central processing unit with our custom Python-based (v.3.9) mlins-package. We used the pydicom package (v.2.3.1) to process the SRH images from the NIO Imaging System. All archived postprocessed image patches were saved as 16-bit TIFF images and handled using the tifffile package (v.2020.10.1). All models were trained using the University of Michigan Advanced Research Computing (ARC) Armis2 high-performance computing cluster. Visual patch and whole-slide encoders were trained on NVIDIA A40 and Titan V100 graphical processing units (GPUs), respectively. Evaluations were performed on NVIDIA Titan V100 GPUs. All custom code for training and inference can be found in our open-source FastGlioma repository. Our models were implemented in PyTorch Lightning (v.1.8.4). We used the ImageNet pretrained ResNet-34 model from torchvision (v.0.14.0). Scikit-learn (v.1.4.1) was used to compute performance metrics on model predictions at both training and inference. Additional dependencies and specifications can be found at our GitHub page (https://github.com/MLNeurosurg/fastglioma).
Ethics and inclusion statement
Our research was approved by the University of Michigan institutional review board (HUM00083059) and the methods were carried out in accordance with the institutional review boardâs guidelines, regulations and policies. All human participants who met the inclusion criteria as stated above were included in the study.
Reporting summary
Further information on research design is available in the Nature Portfolio Reporting Summary linked to this article.