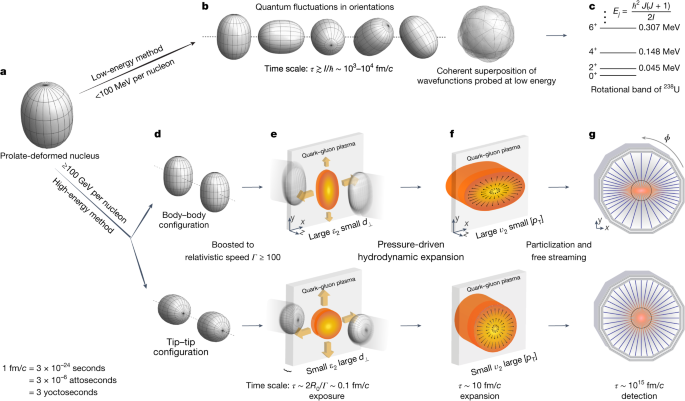
Accessing information in the intrinsic frame
The nuclear shape in the intrinsic frame is not directly observable in low-energy experiments. However, in high-energy collisions, the collective flow phenomenon is sensitive to the shape and size of the nucleon distribution in the overlap region of the transverse plane. This distribution, denoted as \(\rho \left({\bf{r}}\right)\) with râ=âxâ+âiy, provides a direct link to the shape characteristics of the two colliding nuclei in their intrinsic frames, as discussed below.
The elliptic shape of the heavy-ion initial state is characterized by its amplitude ε2 and direction Φ2, defined by nucleon positions as
$${{\mathcal{E}}}_{2}\equiv {\varepsilon }_{2}{{\rm{e}}}^{2{\rm{i}}{\varPhi }_{2}}=\frac{{\int }_{{\bf{r}}}{{\bf{r}}}^{2}\rho \left({\bf{r}}\right)}{{\int }_{{\bf{r}}}| {\bf{r}}{| }^{2}\rho ({\bf{r}})},{\int }_{{\bf{r}}}=\int \,{\rm{d}}x{\rm{d}}y.$$
(4)
When the coordinate system is rotated such that x and y coincide with the minor and major axes, the elliptic eccentricity coincides with the usual definition \({\varepsilon }_{2}=\frac{\langle {y}^{2}\rangle -\langle {x}^{2}\rangle }{\langle {y}^{2}\rangle +\langle {x}^{2}\rangle }\). The parameter ε2 drives the elliptic flow v2: v2âââε2.
Let us now consider collisions at zero impact parameter, in which, without loss of generality, the average elliptic geometry vanishes, that is, \(\langle {{\mathcal{E}}}_{2}\rangle =0\). The second moment of eccentricity over many events is given by53,54
$$\langle {\varepsilon }_{2}^{2}\rangle =\langle {{\mathcal{E}}}_{2}{{\mathcal{E}}}_{2}^{* }\rangle \approx \frac{{\int }_{{{\bf{r}}}_{1},{{\bf{r}}}_{2}}{\left({{\bf{r}}}_{1}\right)}^{2}{\left({{\bf{r}}}_{2}^{* }\right)}^{2}\rho \left({{\bf{r}}}_{1},{{\bf{r}}}_{2}\right)}{{\left({\int }_{{\bf{r}}}| {\bf{r}}{| }^{2}\langle \rho ({\bf{r}})\rangle \right)}^{2}},$$
(5)
where \(\langle \rho ({\bf{r}})\rangle \) represents the event-averaged profile, and
$$\rho \left({{\bf{r}}}_{1},{{\bf{r}}}_{2}\right)=\langle \delta \rho ({{\bf{r}}}_{1})\delta \rho ({{\bf{r}}}_{2})\rangle =\langle \rho ({{\bf{r}}}_{1})\rho ({{\bf{r}}}_{2})\rangle -\langle \rho ({{\bf{r}}}_{1})\rangle \langle \rho ({{\bf{r}}}_{2})\rangle $$
is the usual two-body distribution. Similarly, the third central moments are related to the three-body distribution, \(\rho \left({{\bf{r}}}_{1},{{\bf{r}}}_{2},{{\bf{r}}}_{3}\right)\,=\) \(\langle \delta \rho ({{\bf{r}}}_{1})\delta \rho ({{\bf{r}}}_{2})\delta \rho ({{\bf{r}}}_{3})\rangle \). For example,
$$\langle {\varepsilon }_{2}^{2}\delta {d}_{\perp }/{d}_{\perp }\rangle \approx -\frac{{\int }_{{{\bf{r}}}_{1},{{\bf{r}}}_{2},{{\bf{r}}}_{3}}{({{\bf{r}}}_{1})}^{2}{({{\bf{r}}}_{2}^{\ast })}^{2}|{{\bf{r}}}_{3}^{2}|\rho ({{\bf{r}}}_{1},{{\bf{r}}}_{2},{{\bf{r}}}_{3})}{{({\int }_{{\bf{r}}}|{\bf{r}}{|}^{2}\langle \rho ({\bf{r}})\rangle )}^{3}},$$
(6)
where we define \(\delta {d}_{\perp }/{d}_{\perp }\equiv ({d}_{\perp }-\langle {d}_{\perp }\rangle )/\langle {d}_{\perp }\rangle \), and the relation \(\frac{\delta {d}_{\perp }}{{d}_{\perp }}\approx -\frac{\delta \langle | \,{{\bf{r}}}^{2}\,| \rangle }{\langle | \,{{\bf{r}}}^{2}\,| \rangle }\,=\) \(-\frac{{\int }_{{\bf{r}}}| \,{{\bf{r}}}^{2}\,| \delta \rho \left({\bf{r}}\right)}{{\int }_{{\bf{r}}}| \,{\bf{r}}\,{| }^{2}\langle \rho ({\bf{r}})\rangle }\) is used.
The quantities \({{\mathcal{E}}}_{2}\) and δdâ¥/d⥠depend not only on the nuclear shape but also on the random orientations of the projectile and target nuclei, denoted by Euler angles Ωp and Ωt. For small quadrupole deformation, it suffices to consider the leading-order forms33:
$$\begin{array}{l}\frac{\delta {d}_{\perp }}{{d}_{\perp }}\,\approx \,{\delta }_{d}+{p}_{0}({\varOmega }_{p},{\gamma }_{p}){\beta }_{2p}+{p}_{0}({\varOmega }_{t},{\gamma }_{t}){\beta }_{2t},\\ \,{{\mathcal{E}}}_{2}\,\approx \,{{\mathcal{E}}}_{0}+{{\bf{p}}}_{2}({\varOmega }_{p},{\gamma }_{p}){\beta }_{2p}+{{\bf{p}}}_{2}({\varOmega }_{t},{\gamma }_{t}){\beta }_{2t}.\end{array}$$
(7)
Here, the scalar δd and vector \({{\mathcal{E}}}_{0}\) represent values for spherical nuclei. The values of scalar p0 and vector p2 are directly connected to the xy-projected one-body distribution Ï(r). Therefore, they depend on the orientation of the two nuclei. The fluctuations of δd (\({{\mathcal{E}}}_{0}\)) are uncorrelated with p0 and the fluctuations of \({{\mathcal{E}}}_{0}\) are uncorrelated with p2. After averaging over collisions with different Euler angles and setting β2pâ=âβ2t and γpâ=âγt, we obtain
$$\begin{array}{l}\,\,\,\langle {\varepsilon }_{2}^{2}\rangle \,=\,\langle {\varepsilon }_{0}^{2}\rangle +2\langle {{\bf{p}}}_{2}(\gamma ){{\bf{p}}}_{2}^{* }(\gamma )\rangle {\beta }_{2}^{2}\\ \langle {(\delta {d}_{\perp }/{d}_{\perp })}^{2}\rangle \,=\,\langle {\delta }_{d}^{2}\rangle +2\langle {p}_{0}{(\gamma )}^{2}\rangle {\beta }_{2}^{2}\\ \langle {\varepsilon }_{2}^{2}\delta {d}_{\perp }/{d}_{\perp }\rangle \,=\,\langle {\varepsilon }_{0}^{2}{\delta }_{d}\rangle +2\langle {p}_{0}(\gamma ){{\bf{p}}}_{2}(\gamma ){{\bf{p}}}_{2}{(\gamma )}^{* }\rangle {\beta }_{2}^{3}.\end{array}$$
(8)
It is found that \(\langle {{\bf{p}}}_{2}(\gamma ){{\bf{p}}}_{2}^{* }(\gamma )\rangle \) and \(\langle {p}_{0}{(\gamma )}^{2}\rangle \) are independent of γ, while \(\langle {p}_{0}(\gamma ){{\bf{p}}}_{2}(\gamma ){{\bf{p}}}_{2}{(\gamma )}^{* }\rangle \propto -\cos (3\gamma )\), resulting in expressions in equation (2).
The event-averaged moments in equation (8) are rotationally invariant and capture the intrinsic many-body distributions of \(\rho \left({\bf{r}}\right)\). Note that the coefficients an in equation (2) are strong functions of centrality that decrease towards central collisions, whereas coefficients bn vary weakly with centrality. Therefore, the impact of deformation is always largest in the most central collisions. In general, it can be shown that the n-particle correlations reflect the rotational invariant nth central moments of \(\rho \left({\bf{r}}\right)\), which in turn are connected to the nth moments of the nuclear shape in the intrinsic frame.
Previous experimental attempts on nuclear shapes at high energy
The idea that v2 can be enhanced by β2 was recognized early55,56,57,58,59. Studies at RHIC60 and the LHC61,62,63 in 238Uâ+â238U and 129Xeâ+â129Xe collisions indicated the influence of β2 on v2. Several later theoretical investigations assessed the extent to which β2 can be constrained by v2 alone64,65,66,67. A challenge with v2 is that its a1 term in equation (2) is affected by \({\varepsilon }_{2}^{{\rm{rp}}}\), which often exceeds the \({b}_{1}\,{\beta }_{2}^{2}\) term even in central collisions. A recent measurement of \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) aimed to assess the triaxiality of 129Xe (ref.â42), but the extraction of γXe was hindered by needing previous knowledge of β2Xe and potentially substantial fluctuations in γXe (refs.â39,68,69,70,71). The combination of several observables in this study allows for a more quantitative extraction of nuclear shape parameters.
Event selection
In high-energy experiments, the polar angle θ is usually mapped to the so-called pseudorapidity variable ηâ=ââln(tan(θ/2). The STAR TPC polar angle range â£Î¸âââ90°â£â<â50° corresponds to â£Î·â£â<â1.
The collision events are selected by requiring a coincidence of signals from two vertex position detectors on each side of the STAR barrel, covering a pseudorapidity range of 4.4â<ââ£Î·â£â<â4.9. To increase the statistics for ultra-central collision (UCC) events, a special sample of Auâ+âAu data in 2010 and Uâ+âU data is chosen based on the criteria of high multiplicity in the STAR TPC and minimal activity in the zero-degree calorimeters that cover the beam rapidity72.
In the offline analysis, events are selected to have collision vertices zvtx within 30âcm of the TPC centre along the beamline and within 2âcm of the beam spot in the transverse plane. Furthermore, a selection criterion based on the correlation between the number of TPC tracks and the number of tracks matched to the time-of-flight detector covering â£Î·â£â<â0.9 is applied to suppress pileup events (events containing more than one collision in the TPC)73 and background events.
After applying these selection criteria, the Auâ+âAu dataset has approximately 528 million minimum-bias events (including 370 million in 2011) and 120 million UCC events. The Uâ+âU dataset comprises around 300 million minimum-bias events and 5 million UCC events.
Track selection
For this analysis, tracks are selected with â£Î·â£â<â1 and the transverse momentum range 0.2â<âpTâ<â3.0âGeV/c. To ensure good quality, the selected tracks must have at least 16 fit points out of a maximum of 45, and the ratio of the number of fit points to the number of possible points must be greater than 0.52. Moreover, to reduce contributions from secondary decays, the distance of the closest approach (DCA) of the track to the primary collision vertex must be less than 3âcm.
The tracking efficiency in the TPC was evaluated using the standard STAR Monte Carlo embedding technique74. The efficiencies are nearly independent of pT for pTâ>â0.5âGeV/c, with plateau values ranging from 0.72 in the most central Auâ+âAu collisions and from 0.69 in the most central Uâ+âU collisions to 0.92 in the most peripheral collisions. The efficiency exhibits some pT-dependent variation, of the order of 10% of the plateau values, within the range of 0.2â<âpTâ<â0.5 GeV/c.
Centrality
The centrality of each collision is determined using \({N}_{{\rm{ch}}}^{{\rm{rec}}}\), which represents the number of raw reconstructed tracks in â£Î·â£â<â0.5, satisfying pTâ>â0.15 GeV/c and having more than 10 fit points. After applying a correction to account for the dependence on the collision vertex position and the luminosity, the distribution of \({N}_{{\rm{ch}}}^{{\rm{rec}}}\) is compared with a Monte Carlo Glauber calculation74. This comparison allows for determining centrality intervals, expressed as a percentage of the total nucleusânucleus inelastic cross-section.
Calculation of observables
The \(\langle {v}_{2}^{2}\rangle \), \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \) and \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) are calculated using charged tracks as follows:
$$\begin{array}{rcl}[{p}_{{\rm{T}}}] & = & \frac{{\sum }_{i}{w}_{i}{p}_{{\rm{T}},i}}{{\sum }_{i}{w}_{i}},\langle \langle {p}_{{\rm{T}}}\rangle \rangle \equiv {\langle [{p}_{{\rm{T}}}]\rangle }_{{\rm{evt}}}\\ \langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle & = & {\langle \frac{{\sum }_{i\ne j}{w}_{i}{w}_{j}({p}_{{\rm{T}},i}-\langle \langle {p}_{{\rm{T}}}\rangle \rangle )({p}_{{\rm{T}},j}-\langle \langle {p}_{{\rm{T}}}\rangle \rangle )}{{\sum }_{i\ne j}{w}_{i}{w}_{j}}\rangle }_{{\rm{evt}}}\\ \langle {v}_{2}^{2}\rangle & = & {\langle \frac{{\sum }_{i\ne j}{w}_{i}{w}_{j}\cos (2({\phi }_{i}-{\phi }_{j}))}{{\sum }_{i\ne j}{w}_{i}{w}_{j}}\rangle }_{{\rm{evt}}}\\ \langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle & = & {\langle \frac{{\sum }_{i\ne j\ne k}{w}_{i}{w}_{j}{w}_{k}\cos (2({\phi }_{i}-{\phi }_{j}))({p}_{{\rm{T}},k}-\langle \langle {p}_{{\rm{T}}}\rangle \rangle )}{{\sum }_{i\ne j\ne k}{w}_{i}{w}_{j}{w}_{k}}\rangle }_{{\rm{evt}}}.\end{array}$$
(9)
The averages are performed first on all multiplets within a single event and then over all events in a fixed \({N}_{{\rm{ch}}}^{{\rm{rec}}}\) bin. The track-wise weights wi,j,k account for tracking efficiency and its η and Ï dependent variations. The values of \(\langle {v}_{2}^{2}\rangle \) and \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \) are obtained using the standard method, in which particles i and j are selected from â£Î·â£â<â1, as well as the two-subevent method, in which particles i and j are selected from pseudorapidity ranges of â1â<âηiâ<ââ0.1 and 0.1â<âηjâ<â1, respectively. We also calculate the efficiency-corrected charged particle multiplicity in â£Î·â£â<â0.5, defined as Nchâ=ââiwi. This observable is used to evaluate the systematics.
The covariance \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) is calculated by averaging over all triplets labelled by particle indices i, j and k. The standard cumulant framework is used to obtain the results instead of directly calculating all triplets41. We also calculated \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) using the two-subevent method42, in which particles i and j are taken from ranges of â1â<âηiâ<ââ0.1 and 0.1â<âηjâ<â1, whereas particle k is taken from either subevents. Including a pseudorapidity gap between the particle pairs or triplets suppresses the short-range non-flow correlations arising from resonance decays and jets75.
The calculation of \({\rho }_{2}=\frac{\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle }{\langle {v}_{2}^{2}\rangle \sqrt{\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle }}\) relies on the input values of \(\langle {v}_{2}^{2}\rangle \), \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \) and \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \). These components and Ï2 are shown in Extended Data Fig. 1 as a function of centrality. In the central region, enhancements of \(\langle {v}_{2}^{2}\rangle \) and \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \) are observed in Uâ+âU relative to Auâ+âAu collisions, which is consistent with the influence of large β2U. By contrast, the values of \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) are markedly suppressed in Uâ+âU compared with Auâ+âAu collisions across the entire centrality range shown. This suppression is consistent with the negative contribution expected for strong prolate deformation of U as described in equation (2).
In this analysis, the default results are obtained using the two-subevent method. The differences between the standard and two-subevent methods are used to evaluate the impact of non-flow correlations discussed below.
Influence of non-flow correlations
An important background in our measurement is non-flow: correlations among a few particles originated from a common source, such as resonance decays and jets, which are uncorrelated with the initial geometry. Two approaches are used to estimate the non-flow contributions. Non-flow correlations are short-range in η and can be suppressed by the subevent method by requiring a rapidity gap between the pairs or triplets of particles in equation (9). Hence, in the first approach, the differences between the standard and subevent methods provide an estimate of the non-flow contribution. However, part of the rapidity gap dependence of the signal in central collisions may arise from longitudinal fluctuations in [pT] and v2 because of variations in the initial geometry in η (ref.â42).
The second approach assumes that the clusters causing non-flow correlations are mutually independent. In this independent-source scenario, non-flow in n-particle cumulants is expected to be diluted by the charged particle multiplicity as \(1/{N}_{{\rm{ch}}}^{n-1}\) (ref.â76). Therefore, non-flow (nf) contributions in a given centrality can be estimated by
$$\begin{array}{l}{\langle {v}_{2}^{2}\rangle }_{{\rm{nf}}}\approx \frac{{\left[\langle {v}_{2}^{2}\rangle {N}_{{\rm{ch}}}\right]}_{{\rm{peri}}}}{{N}_{{\rm{ch}}}},\\ {\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle }_{{\rm{nf}}}\approx \frac{{\left[\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle {N}_{{\rm{ch}}}\right]}_{{\rm{peri}}}}{{N}_{{\rm{ch}}}},\\ {\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle }_{{\rm{nf}}}\approx \frac{{\left[\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle {N}_{{\rm{ch}}}^{2}\right]}_{{\rm{peri}}}}{{N}_{{\rm{ch}}}^{2}}\end{array}$$
(10)
where the subscript âperiâ is a label for the peripheral bin. This procedure makes two assumptions that are not fully valid: (1) the signal in the peripheral bin is all non-flow and (2) non-flow in other centralities is unmodified by final state medium effects. For example, the medium effects strongly suppress the jet yield and modify the azimuthal structure of non-flow correlations. Hence, this approach provides only a qualitative estimate of the non-flow. Moreover, this approach is not applicable for \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \), as medium effects are expected to reduce the momentum differences of non-flow particles as they are out of local equilibrium.
Extended Data Fig. 2 shows the Nch-scaled values of \(\langle {v}_{2}^{2}\rangle \), \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \) and \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) as a function of centrality in Auâ+âAu collisions. The requirement of subevent reduces the signal in the most peripheral bin by 50%, 40% and 80%, respectively, which can be treated as the amount of non-flow rejected by the subevent requirement. Therefore, we use the differences between the standard and subevent methods to estimate the non-flow in the subevent method. These differences vary with centrality because of the combined effects of medium modification of non-flow and longitudinal flow decorrelations77. These differences are propagated to the ratios of these observables between Uâ+âU and Auâ+âAu. They are found to be 1.1%, 3.5% and 11% for \({R}_{{v}_{2}^{2}}\), \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\) and \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\), respectively.
Extended Data Fig. 2 also provides an estimate of non-flow based on the Nch-scaling method. We assume that the entire signals in the 80â100% centrality in two-subevent are non-flow, and then use equation (10) to estimate the fraction of non-flow as a function of centrality. As mentioned earlier, we use this approach for \(\langle {v}_{2}^{2}\rangle \) and \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \), in which the medium effects may redistribute non-flow correlations in azimuthal angle, instead of suppressing them. This approach is unsuitable for \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \), for which the medium effects should always suppress the non-flow contribution. In the 0â5% most central collisions, the estimated non-flow is about 6% for \(\langle {v}_{2}^{2}\rangle \) and only about 1.4% for \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \). These differences, when propagated to the ratios, are reduced for \({R}_{{v}_{2}^{2}}\), which is positive, and increased for \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\), which is negative. They amount to about 2.8% for \({R}_{{v}_{2}^{2}}\) and 2.5% for \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\).
The non-flow systematic uncertainties are taken as the larger of the two approaches for \({R}_{{v}_{2}^{2}}\) and \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\), whereas for \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\), the difference between standard and subevent methods is used. The total non-flow uncertainties in the 0â5% centrality are 2.8%, 3.5% and 11% for \({R}_{{v}_{2}^{2}}\), \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\) and \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\), respectively.
Extended Data Fig. 3 contrasts the non-flow systematic uncertainties with other sources of uncertainties (next section) in this analysis. In the 0â5% centrality, the non-flow uncertainties are comparable or slightly larger than other sources, whereas they are subdominant in other centrality ranges.
In the literature, non-flow contributions are sometimes estimated using the HIJING model78, which has only non-flow correlations. The latter were found to follow very closely equation (10) (refs.â79,80). In our second approach, instead of relying on the HIJING model, we assume this Nch-scaling behaviour but use real peripheral data as the baseline for non-flow contributions. Our findings indicate that the HIJING model fails to quantitatively capture the features of non-flow. Specifically, the HIJING model predicts a much weaker Îη dependence for \(\langle {v}_{2}^{2}\rangle \), with only a 13% difference between the standard and two-subevent methods, whereas the data indicate a 50% decrease81 (fig. 25 in ref.â81 for pâ+âp collisions). Furthermore, we found that the values of \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) predicted by HIJING are three times larger than the data in peripheral Auâ+âAu collisions. Therefore, the non-flow estimation based on the HIJING model in ref.â80 seems to be exaggerated. A more recent estimate46, based on a transport model incorporating full medium dynamics and equation (10), yields a non-flow fraction consistent with STAR data. This study also suggests a potential increase of the \({R}_{{v}_{2}^{2}}\) with Îη associated with flow decorrelation effects.
Understanding non-flow correlations as a physical process has always been a work in progress. As our knowledge deepens, the non-flow uncertainties are expected to reduce. Rather than merely contributing to experimental uncertainties or even being corrected for in the data, non-flow physics should ultimately be incorporated into hydrodynamic models. Currently, these models include non-flow effects from resonance decays but lack contributions from jet fragmentation.
Systematic uncertainties
Systematic uncertainties include an estimate of the non-flow contributions discussed above and other sources accounting for detector effects and analysis procedure. These other sources are estimated by varying the track quality selections, the zvtx cuts, examining the influence of pileup, comparing results from periods with different detector conditions and closure test. The influence of track selection criteria is studied by varying the number of fit hits on the track from a minimum of 16 to 19 and by varying DCA cut from <3âcm to <2.5âcm, resulting in variations of 1â5% for \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \). The impacts on \(\langle {v}_{2}^{2}\rangle \) and \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) are up to 2.5% and 4%, respectively.
The influence of track reconstruction on the collision vertex is examined by comparing the results for different â£zvtx⣠cuts, with variations found to be 0.5â3% for all observables. Comparisons between data-taking periods, particularly normal and reverse magnetic field runs in Auâ+âAu collisions, show consistency within their statistical uncertainties. The influence of pileup and background events is studied by varying the cut on the correlation between \({N}_{{\rm{ch}}}^{{\rm{rec}}}\) and the number of hits in the TOF. The influence is found to be 1â3% for \(\langle {v}_{2}^{2}\rangle \) and \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \), and reaches 2â10% for \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \). Comparisons are also made between the 2010 and 2011 Auâ+âAu datasets, which have different active acceptances in the TPC. The results are largely consistent with the quoted uncertainties, although some differences are observed, particularly in the central region, in which variations reach 5â10% for \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \).
A closure test was conducted, in which the reconstruction efficiency and its variations in η and Ï from the data were used to retain a fraction of the particles generated from a multi-phase transport model82. Subsequently, a track-by-track weight, as described in equation (9), was applied to the accepted particles. All observables are calculated using the accepted particles and compared with those obtained using the original particles. This procedure allowed us to recover \(\langle {v}_{2}^{2}\rangle \) and \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \) within their statistical uncertainties. However, a 2â3% nonclosure was observed in \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \). Nevertheless, it is important to note that such non-closures largely cancel when considering the ratios between Uâ+âU and Auâ+âAu collisions.
Several additional cross-checks were carried out. The track reconstruction efficiency has about 5% uncertainty because of its reliance on particle type and occupancy dependence. We repeated the analysis by varying this efficiency, and the variations in the results were either less than 1% or consistent within their statistical uncertainties. The reconstructed pT can differ from the true value because of finite momentum resolution. This effect was investigated by smearing the reconstructed pT according to the known resolution, calculating the observable and comparing the results with the original ones. A discrepancy of approximately 0.5% was observed for \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \), whereas other observables remained consistent within their statistical uncertainties. These effects cancel in the ratios between °Uâ+âU and Auâ+âAu collisions.
The default results are obtained from the two-subevent method. The total systematic uncertainties, including these sources and non-flow, are calculated as a function of centrality. The uncertainties of the ratios between Uâ+âU and Auâ+âAu are evaluated for each source and combined in quadrature to form the total systematic uncertainties. This process results in a partial cancellation of the uncertainties between the two systems. The uncertainties from different sources discussed above on the ratios are shown by the black boxes in Extended Data Fig. 3. The total systematic uncertainties, including non-flow in the 0â5% centrality range, amount to 3.9%, 4.4% and 12.5% for \({R}_{{v}_{2}^{2}}\), \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\), and \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\), respectively.
Hydrodynamic model setup and simulation
Extended Data Table 1 details the WoodsâSaxon parameters for Au and U used in the IP-Glasmaâ+âMUSIC model calculations. The nucleonânucleon inelastic cross-sections are the standard values 42âmb and 40.6âmb for Auâ+âAu collisions at 200âGeV and Uâ+âU collisions at 193âGeV, respectively. For U, the nuclear shape in equation (1) is extended to include a possible small axial hexadecapole deformation β4:
$$R(\theta ,\phi )={R}_{0}(1+{\beta }_{2}[\cos \gamma {Y}_{2,0}+\sin \gamma {Y}_{2,2}]+{\beta }_{4}{Y}_{4,0}).$$
(11)
Most low-energy nuclear structure models favour a modest oblate deformation for 197Au (ref.â34). We assume β2Auâ=â0.14 and γAuâ=â45° as the default choice for 197Au, which are varied in the range of β2Auâââ0.12â0.14 and γAuâââ37â53° according to refs.â34,67. These calculations reasonably reproduce many observables related to the ground-state nuclear deformation. For 238U, we scan several β2U values ranging from 0 to 0.34. We also vary β4U from 0 to 0.09 and γU in the range of 0°â20° to examine the sensitivity of the Uâ+âU results to hexadecapole deformation and triaxiality. For each setting, about 100,000â400,000 events are generated using the officially available IP-Glasmaâ+âMUSIC25,44. Each event is oversampled at least 100 times to minimize statistical fluctuations in the hadronic transport. These calculations were performed using services provided by the Open Science Grid Consortium83,84.
The role of final state effects is studied by varying the shear and bulk viscosities simultaneously up and down by 50%. The impacts on \(\langle {v}_{2}^{2}\rangle \), \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \) and \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) are shown for Auâ+âAu collisions in Extended Data Fig. 4 (top). The values of these flow observables are changed by more than a factor of two as a function of centrality. Yet, the ratios between Uâ+âU and Auâ+âAu collisions (Extended Data Fig. 4, bottom) are relatively stable. A small reduction of \({R}_{{v}_{2}^{2}}\) and \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\) are observed in non-central collisions, when values of viscosities are halved. However, this change is an overestimate because the calculated flow observables greatly overestimate the data. So, in the end, half of the variations of the ratios are included in the model uncertainty.
The main theoretical uncertainties arise from variations in nuclear structure parameters. Parameters common between two collision systems, such as the minimum inter-nucleon distance in nuclei dmin, are not expected to contribute to the uncertainty significantly. However, other parameters, including nuclear radius R0, skin a and higher-order hexadecapole deformation β4, could be different between Au and U and hence contribute more to the theoretical uncertainty.
Extended Data Table 1 provides a list of variations of nuclear structure parameters. The impact of these variations on ratios of flow observables is shown in Extended Data Fig. 5. The ratios of flow observables are insensitive to these variations in the most central collisions. \({R}_{{v}_{2}^{2}}\) is particularly sensitive to skin parameter a. This is understandable, as v2 has a large contribution from the reaction plane flow, which varies strongly with the value of a (ref.â45).
Model uncertainties for the ratios are derived by combining the impact of varying viscosities, together with various sources from Extended Data Fig. 5. As a consequence, checks that are consistent with the default calculation within their statistical uncertainties do not contribute to the model uncertainties. The combined model uncertainties for 1 standard deviation are shown in Fig. 3.
A cross-check is conducted for an alternative hydrodynamic code, the Trajectum model22,85. This model has 20 parameter sets obtained from a Bayesian analysis of the Pbâ+âPb data at the LHC but was not tuned to the RHIC data. For this calculation, we simply repeat the calculation at RHIC energy and calculate the same observables. Although the description of \(\langle {v}_{2}^{2}\rangle \) and \(\langle {(\delta {p}_{{\rm{T}}})}^{2}\rangle \) is reasonable, several parameter sets give negative values of \(\langle {v}_{2}^{2}\delta {p}_{{\rm{T}}}\rangle \) in mid-central collisions, and are subsequently not used. The calculation is performed for the remaining 16 parameter sets as a function of centrality, and root mean square variations among these calculations are assigned as the uncertainty.
Extended Data Fig. 6 shows the ratios of flow observables from Trajectum and compares them with IP-Glasmaâ+âMUSIC. The results from these two models agree in their uncertainties for \({R}_{{v}_{2}^{2}}\) and \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\), with Trajectum predictions slightly higher in the UCC region. This leads to slightly lower values of β2U than the IP-Glasma model: β2Uâ=â0.228â±â0.013 for \({R}_{{v}_{2}^{2}}\) and β2U =â0.276 ±â0.018 for \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\).
For \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\), however, the Trajectum model tends to systematically underpredict the data, as well as has much larger uncertainties compared with the IP-Glasma model. In central collisions, this discrepancy can be improved by using a larger triaxiality parameter value γUâ~â15°. Overall, the comparison of the Trajectum model with data gives similar constraints on β2U with comparable uncertainties but a larger γU value with bigger uncertainties (next section).
Assigning uncertainties on β
2U and γ
U
A standard pseudo-experiment procedure, similar to that in ref.â86, is used to combine the uncertainties from \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\) and \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\) shown in Fig. 3g. We assume that the total uncertainties extracted from the two observables are independent, and we model the probability density function as follows:
$$P({\beta }_{2{\rm{U}}},{\gamma }_{{\rm{U}}})\propto \exp \,\left(-\frac{{({\beta }_{2{\rm{U}}}-{\bar{\beta }}_{a})}^{2}}{2{\sigma }_{a}^{2}}-\frac{{({\beta }_{2{\rm{U}}}-{\bar{\beta }}_{b}({\gamma }_{{\rm{U}}}))}^{2}}{2{\sigma }_{b}^{2}({\gamma }_{{\rm{U}}})}\right).$$
(12)
Here, \({\bar{\beta }}_{a}=0.294\) and Ïa = 0.021 represent the mean and uncertainty of β2U extracted from \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\) in Fig. 3g from the IP-Glasmaâ+âMUSIC model. Similarly, \({\bar{\beta }}_{b}\) and Ïb are the mean and uncertainty of β2U from \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\), and they depend on the parameter γU. We sample a uniform prior distribution in β2U and γU to obtain the posterior distribution. From this posterior distribution, we obtained the mean and 1 standard deviation uncertainty of β2U and γU, β2Uâ=â0.297â±â0.015 and γUâ=â8.5°â±â4.8°, as well as the confidence contours shown in Fig. 3g. This statistical analysis is also performed for \({R}_{{(\delta {p}_{{\rm{T}}})}^{2}}\) and \({R}_{{v}_{2}^{2}\delta {p}_{{\rm{T}}}}\) for the Trajectum model, yielding constraints of β2Uâ=â0.275â±â0.017 and γUâ=â15.5°â± 7.8°.
Finally, we perform an analysis to combine the constraints of the IP-Glasmaâ+âMUSIC and Trajectum models. This is achieved by multiplying the probability density function equation (12) from the two models, treating their constraints as statistically independent. This approach yields β2Uâ=â0.286â±â0.012 and γUâ=â8.7°â±â4.5°. We noticed that the Trajectum model does not affect the constraints on γU because of the large uncertainty of the model, but the uncertainty on β2U reduces markedly because of the comparable precision in the two models. Therefore, we also include the difference of the extracted β2U values between the two models as an additional theoretical uncertainty. The final constraints given by this procedure are β2Uâ=â0.286â±â0.025 and γUâ=â8.7°â±â4. 5°.